NEET Exam > NEET Notes > NCERT Exemplar & Revision Notes for NEET > Revision Notes: Kinetic Theory of Gases
Kinetic Theory of Gases Class 11 Notes Physics
- Kinetic Theory of Matter:-
(a) Solids:- It is the type of matter which has got fixed shape and volume. The force of attraction between any two molecules of a solid is very large.
(b) Liquids:- It is the type of matter which has got fixed volume but no fixed shape. Force of attraction between any two molecules is not that large as in case od solids.
(c) Gases:- It is the type of matter does not have any fixed shape or any fixed volume. - Ideal Gas:- A ideal gas is one which has a zero size of molecule and zero force of interaction between its molecules.
- Ideal Gas Equation:- A relation between the pressure, volume and temperature of an ideal gas is called ideal gas equation.
PV/T = Constant or PV = nRT
Here, n is the number of moles and R is the universal gas constant.
- Gas Constant:-
(a) Universal gas constant (R):-
R= P0 V0/T0
=8.311 J mol-1K-1
(b) Specific gas constant (r):-
PV= (R/M) T = rT,
Here, r = R/M - Real Gas:-The gases which show deviation from the ideal gas behavior are called real gas.
- Vander wall’s equation of state for a real gas:-
[P+(na/V)2?][V-nb] = nRT
Here n is the number of moles of gas. - Avogadro’s number (N):- Avogadro’s number (N), is the number of carbon atoms contained in 12 gram of carbon-12.
N = 6.023×1023
(a) To calculate the mass of an atom/molecule:-
Mass of one atom = atomic weight (in gram)/N
Mass of one molecule = molecular weight (in gram)/N
(b) To calculate the number of atoms/molecules in a certain amount of substance:-
Number of atoms in m gram = (N/atomic weight)×m
Number of molecules in m gram = (N/molecular weight)×m
(c) Size of an atom:-
Volume of the atom, V = (4/3)πr3
Mass of the atom, m = A/N
Here, A is the atomic weight and N is the Avogadro’s number.
Radius, r =[3A/4πNρ]1/3\
Here ρ is the density. - Gas laws:-
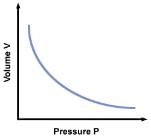
(a) Boyle’s law:- It states that the volume of a given amount of gas varies inversely as its pressure, provided its temperature is kept constant.
PV = Constant
(b) Charlers law or Gey Lussac’s law:- It states that volume of a given mass of a gas varies directly as its absolute temperature, provided its pressure is kept constant.
V/T= Constant
V–V0/V0t = 1/273 = γp
Here γp (=1/273) is called volume coefficient of gas at constant pressure.
Volume coefficient of a gas, at constant pressure, is defined as the change in volume per unit volume per degree centigrade rise of temperature.
(c) Gay Lussac’s law of pressure:- It states that pressure of a given mass of a gas varies directly as its absolute temperature provided the volume of the gas is kept constant.
P/T = P0/T0 or P – P0/P0t = 1/273 = γp
Here γp (=1/273) is called pressure coefficient of the gas at constant volume.
Pressure coefficient of a gas, at constant volume, is defined as the change in pressure per unit pressure per degree centigrade rise of temperature.
(d) Dalton’s law of partial pressures:-
Partial pressure of a gas or of saturated vapors is the pressure which it would exert if contained alone in the entire confined given space.
P= p1+p2+p3+……..
nRT/V = p1+p2+p3+……..
(e) Grahm’s law of diffusion:- Grahm’s law of diffusion states that the rate of diffusion of gases varies inversely as the square root of the density of gases.
R∝1/√ρ or R1/R2 =√ρ2/ ρ1
So, a lighter gas gets diffused quickly.
(f) Avogadro’s law:- It states that under similar conditions of pressure and temperature, equal volume of all gases contain equal number of molecules.
For m gram of gas, PV/T = nR = (m/M) R - Pressure of a gas (P):- P = 1/3 (M/V) C2 = 1/3 (ρ) C2
- Root mean square (r.m.s) velocity of the gas:- Root mean square velocity of a gas is the square root of the mean of the squares of the velocities of individual molecules.
C= √[c12+ c22+ c32+…..+ cn2]/n = √3P/ ρ - Pressure in terms of kinetic energy per unit volume:- The pressure of a gas is equal to two-third of kinetic energy per unit volume of the gas.
P= 2/3 E - Kinetic interpretation of temperature:- Root mean square velocity of the molecules of a gas is proportional to the square root of its absolute temperature.
C= √3RT/M
Root mean square velocity of the molecules of a gas is proportional to the square root of its absolute temperature.
At, T=0, C=0
Thus, absolute zero is the temperature at which all molecular motion ceases. - Kinetic energy per mole of gas:-
K.E. per gram mol of gas = ½ MC2 = 3/2 RT - Kinetic energy per gram of gas:-
½ C2 = 3/2 rt
Here, ½ C2 = kinetic energy per gram of the gas and r = gas constant for one gram of gas. - Kinetic energy per molecule of the gas:-
Kinetic energy per molecule = ½ mC2 = 3/2 kT
Here, k (Boltzmann constant) = R/N
Thus, K.E per molecule is independent of the mass of molecule. It only depends upon the absolute temperature of the gas. - Regnault’s law:- P∝T
- Graham’s law of diffusion:-
R1/R2 = C1/C2 = √ρ2/ ρ1 - Distribution of molecular speeds:-
(a) Number of molecules of gas possessing velocities between v and v+dv :-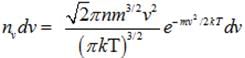
(b) Number of molecules of gas possessing energy between u and u+dv:-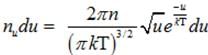
(c) Number of molecules of gas possessing momentum between p and p+dp :-
(d) Most probable speed:- It is the speed, possessed by the maximum number of molecules of a gas contained in an enclosure.
Vm= √[2kT/m]
(e) Average speed (Vav):- Average speed of the molecules of a gas is the arithmetic mean so the speeds of all the molecules.
Vav= √[8kT/πm]
(f) Root mean square speed (Vrms):- It is the square root of the mean of the squares of the individual speeds of the molecules of a gas.
Vrms = √[3kT/m]
Vrms > Vav > Vm - Degree of Freedom (n):- Degree of freedom, of a mechanical system, is defined as the number of possible independent ways, in which the position and configuration of the system may change.
In general, if N is the number of particles, not connected to each other, the degrees of freedom n of such a system will be,
n = 3N
If K is the number of constraints (restrictions), degree of freedom n of the system will be,
n = 3N –K - Degree of freedom of a gas molecule:-
(a) Mono-atomic gas:- Degree of freedom of monoatomic molecule, n = 3
(b) Di-atomic gas:-
At very low temperature (0-250 K):- Degree of freedom, n = 3
At medium temperature (250 K – 750 K):- Degree of freedom, n = 5 (Translational = 3, Rotational = 2)
At high temperature (Beyond 750 K):- Degree of freedom, n = 6 (Translational = 3, Rotational = 2, Vibratory =1), For calculation purposes, n = 7 - Law of equipartition of energy:- In any dynamical system, in thermal equilibrium, the total energy is divided equally among all the degrees of freedom and energy per molecule per degree of freedom is ½ kT.
E = ½ kT - Mean Energy:- K.E of one mole of gas is known as mean energy or internal energy of the gas and is denoted by U.
U = n/2 RT
Here n is the degree of freedom of the gas.
(a) Mono-atomic gas(n = 3):- U = 3/2 RT
(b) Diatomic gas:-
At low temperature (n=3):- U = 3/2 RT
At medium temperature (n=5):- U = 5/2 RT
At high temperature (n=7):- U = 7/2 RT - Relation between ratio of specific heat capacities (γ) and degree of freedom (n):-
γ = Cp/Cv = [1+(2/n)]
(a) For mono-atomic gas (n=3):- γ = [1+(2/n)] = 1+(2/3) = 5/3=1.67
(b) For diatomic gas (at medium temperatures (n=5)):- γ = [1+(2/5)] = 1+(2/5) = 7/5=1.4
(c) For diatomic gas (at high temperatures (n=7)):- γ = [1+(2/7)] = 9/7 = 1.29
The document Kinetic Theory of Gases Class 11 Notes Physics is a part of the NEET Course NCERT Exemplar & Revision Notes for NEET.
All you need of NEET at this link: NEET
FAQs on Kinetic Theory of Gases Class 11 Notes Physics
| 1. What is the kinetic theory of gases? |  |
Ans. The kinetic theory of gases states that gases are composed of a large number of tiny particles, such as atoms or molecules, which are in constant random motion. This theory helps explain the macroscopic properties of gases, such as pressure, temperature, and volume.
| 2. How does the kinetic theory of gases explain pressure? |  |
Ans. According to the kinetic theory of gases, the pressure exerted by a gas is a result of the collisions between the gas particles and the walls of the container. The more frequent and energetic the collisions, the higher the pressure. This is why increasing the number of gas particles or their speed increases the pressure.
| 3. What is the relationship between temperature and the kinetic energy of gas particles? |  |
Ans. The kinetic theory of gases states that the temperature of a gas is directly proportional to the average kinetic energy of its particles. As the temperature increases, the average kinetic energy of the gas particles also increases. Conversely, as the temperature decreases, the average kinetic energy decreases.
| 4. How does the kinetic theory of gases explain the expansion and contraction of gases with changes in temperature? |  |
Ans. The kinetic theory of gases explains the expansion and contraction of gases with changes in temperature by considering the motion of gas particles. When the temperature of a gas increases, the average kinetic energy of the particles increases, causing them to move faster and collide more frequently with the container walls, leading to expansion. Conversely, when the temperature decreases, the average kinetic energy decreases, resulting in slower particle motion and contraction of the gas.
| 5. How does the kinetic theory of gases explain the diffusion of gases? |  |
Ans. According to the kinetic theory of gases, diffusion occurs due to the random motion of gas particles. Gas particles move in all directions, and when there is a concentration gradient, they tend to move from areas of higher concentration to areas of lower concentration. This random motion and collision of particles lead to the gradual mixing and spreading out of gases, resulting in diffusion.
Related Searches





















