Rigid Body Rotation | Civil Engineering Optional Notes for UPSC PDF Download
Kinematics
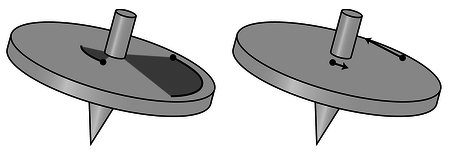
When a rigid object rotates, every part of it (every atom) moves in a circle, covering the same angle in the same amount of time, a. Every atom has a different velocity vector, b. Since all the velocities are different, we can't measure the speed of rotation of the top by giving a single velocity. We can, however, specify its speed of rotation consistently in terms of angle per unit time. Let the position of some reference point on the top be denoted by its angle θ, measured in a circle around the axis. For reasons that will become more apparent shortly, we measure all our angles in radians. Then the change in the angular position of any point on the top can be written as dθ, and all parts of the top have the same value of dθ over a certain time interval dt. We define the angular velocity, ω (Greek omega),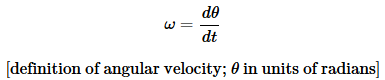
which is similar to, but not the same as, the quantity ω we defined earlier to describe vibrations. The relationship between ω and t is exactly analogous to that between x and t for the motion of a particle through space.
Relations between angular quantities and motion of a point
It is often necessary to be able to relate the angular quantities to the motion of a particular point on the rotating object. As we develop these, we will encounter the first example where the advantages of radians over degrees become apparent.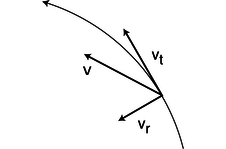
Figure 4.2.3: We construct a coordinate system that coincides with the location and motion of the moving point of interest at a certain moment.
The speed at which a point on the object moves depends on both the object's angular velocity ω and the point's distance r from the axis. We adopt a coordinate system, d, with an inward (radial) axis and a tangential axis. The length of the infinitesimal circular arc ds traveled by the point in a time interval dt is related to dθ by the definition of radian measure, dθ = ds/rdθ r, where positive and negative values of ds represent the two possible directions of motion along the tangential axis. We then have 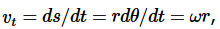 or
or 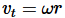
The radial component is zero, since the point is not moving inward or outward,
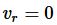
Dynamics
If we want to connect all this kinematics to anything dynamical, we need to see how it relates to torque and angular momentum. Our strategy will be to tackle angular momentum first, since angular momentum relates to motion, and to use the additive property of angular momentum: the angular momentum of a system of particles equals the sum of the angular momenta of all the individual particles. The angular momentum of one particle within our rigidly rotating object, L= mv⊥rr, can be rewritten as L=rpsinθ, where r and p are the magnitudes of the particle's r and momentum vectors, and θ is the angle between these two vectors. (The r vector points outward perpendicularly from the axis to the particle's position in space.) In rigid-body rotation the angle θ is 90°, so we have simply L=rpLrp. Relating this to angular velocity, we have
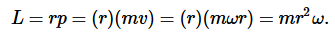
The particle's contribution to the total angular momentum is proportional to ω, with a proportionality constant mr. We refer to mr as the particle's contribution to the object's total moment of inertia, I, where “moment” is used in the sense of “important,” as in “momentous” --- a bigger value of I tells us the particle is more important for determining the total angular momentum. The total moment of inertia is

The angular momentum of a rigidly rotating body is then
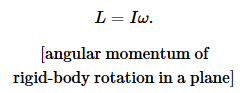
Iterated integrals
In various places in this book, we'll come across integrals stuck inside other integrals. These are known as iterated integrals, or double integrals, triple integrals, etc. Similar concepts crop up all the time even when you're not doing calculus, so let's start by imagining such an example. Suppose you want to count how many squares there are on a chess board, and you don't know how to multiply eight times eight. You could start from the upper left, count eight squares across, then continue with the second row, and so on, until you how counted every square, giving the result of 64. In slightly more formal mathematical language, we could write the following recipe: for each row, r, from 1 to 8, consider the columns, c, from 1 to 8, and add one to the count for each one of them. Using the sigma notation, this becomes
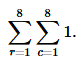
If you're familiar with computer programming, then you can think of this as a sum that could be calculated using a loop nested inside another loop. To evaluate the result (again, assuming we don't know how to multiply, so we have to use brute force), we can first evaluate the inside sum, which equals 8, giving
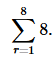
Notice how the “dummy” variable c has disappeared. Finally we do the outside sum, over r, and find the result of 64.
Now imagine doing the same thing with the pixels on a TV screen. The electron beam sweeps across the screen, painting the pixels in each row, one at a time. This is really no different than the example of the chess board, but because the pixels are so small, you normally think of the image on a TV screen as continuous rather than discrete. This is the idea of an integral in calculus. Suppose we want to find the area of a rectangle of width a and height b, and we don't know that we can just multiply to get the area ab. The brute force way to do this is to break up the rectangle into a grid of infinitesimally small squares, each having width dx and height dy, and therefore the infinitesimal area dA = dxdy. For convenience, we'll imagine that the rectangle's lower left corner is at the origin. Then the area is given by this integral:
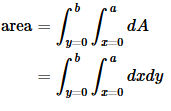
Notice how the leftmost integral sign, over y, and the rightmost differential, dy, act like bookends, or the pieces of bread on a sandwich. Inside them, we have the integral sign that runs over x, and the differential dx that matches it on the right. Finally, on the innermost layer, we'd normally have the thing we're integrating, but here's it's 1, so I've omitted it. Writing the lower limits of the integrals with x = and y = helps to keep it straight which integral goes with with differential. The result is
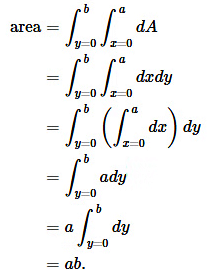
Finding moments of inertia by integration
Moment of inertia of a thin rod
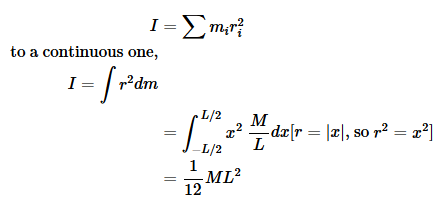
In this example the object was one-dimensional, which made the math simple. The next example shows a strategy that can be used to simplify the math for objects that are three-dimensional, but possess some kind of symmetry.
Moment of inertia of a disk
What is the moment of inertia of a disk of radius b, thickness t, and mass M, for rotation about its central axis?
We break the disk down into concentric circular rings of thickness dr. Since all the mass in a given circular slice has essentially the same value of r (ranging only from r to r+dr), the slice's contribution to the total moment of inertia is simply r2dm. We then have
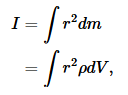
where V=πb2t is the total volume, ρ = M/V = M/πb2 is the density, and the volume of one slice can be calculated as the volume enclosed by its outer surface minus the volume enclosed by its inner surface, dV=π(r+dr)2t−πr2t=2πtrdr.
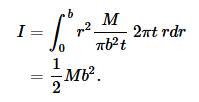
In the most general case where there is no symmetry about the rotation axis, we must use iterated integrals, as discussed in subsection 4.2.4. The example of the disk possessed two types of symmetry with respect to the rotation axis: (1) the disk is the same when rotated through any angle about the axis, and (2) all slices perpendicular to the axis are the same. These two symmetries reduced the number of layers of integrals from three to one. The following example possesses only one symmetry, of type (2), and we simply set it up as a triple integral. You may not have seen multiple integrals yet in a math course. If so, just skim this example.
Moment of inertia of a cube
What is the moment of inertia of a cube of side b, for rotation about an axis that passes through its center and is parallel to four of its faces? Let the origin be at the center of the cube, and let x be the rotation axis.
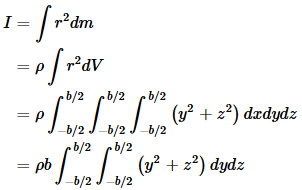
The fact that the last step is a trivial integral results from the symmetry of the problem. The integrand of the remaining double integral breaks down into two terms, each of which depends on only one of the variables, so we break it into two integrals,
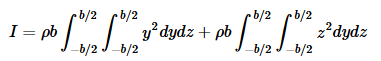
which we know have identical results. We therefore only need to evaluate one of them and double the result:
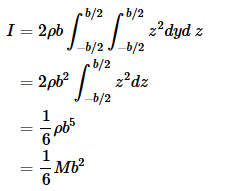
|
350 videos|464 docs|2 tests
|
FAQs on Rigid Body Rotation - Civil Engineering Optional Notes for UPSC
| 1. How can iterated integrals be used to find moments of inertia in rigid body rotation? |  |
| 2. What is the significance of finding moments of inertia in rigid body rotation? |  |
| 3. How does the process of integration help in determining the moments of inertia of complex shapes? |  |
| 4. Can moments of inertia be calculated using alternative methods besides integration? |  |
| 5. How can knowledge of moments of inertia obtained through integration be applied in real-world engineering and physics applications? |  |





















