Sampling Distributions | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Properties of the Sampling Distribution of the Mean |

|
| Applications of Sampling Distribution |

|
| Conclusion |

|
Introduction
- Sampling distribution, also known as finite-sample distribution, represents the probability distribution of a specific statistic derived from a random sample. These distributions hold significant importance in statistics as they simplify the process of drawing statistical inferences. Essentially, they allow analytical considerations to be based on the sampling distribution of a statistic rather than the joint probability distribution of all individual sample values.
- In essence, the sampling distribution emerges from the collection of real data. An essential characteristic of a sample is its finite nature, denoted by the countable number of scores represented by the letter 'n'. The value of a statistic varies across different samples, rendering it a random variable. Consequently, the probability distribution associated with it is referred to as its sampling distribution.
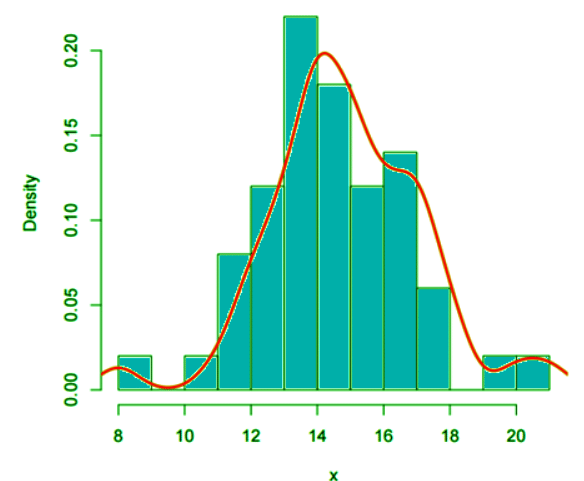
For example, consider the following dataset that contributes to the development of a sampling distribution:
15 14 15 18 15 20 15 16 17 14 17 13 11 14 18 12 17 12 21 8 14 17 14 12 13 15 15 16 17 14 16 13 14 15 18 16 16 17 14 15 16 15 17 12 14 14 13 13 13 14
This dataset serves as a basis for analyzing the sampling distribution.
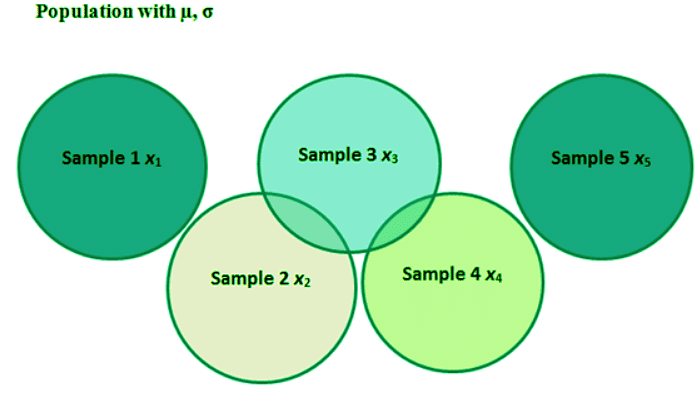
In the given illustration, the rectangle symbolizes a sizable population, with each circle depicting a sample of size 'n'. Since the entries in each sample may vary, the sample means can also exhibit variations. For instance, the mean of Sample 1 is denoted as 'x1', Sample 2 as 'x2', and so forth. The sampling distribution, comprising the sample means of size 'n' for this population, encompasses 'x1', 'x2', 'x3', and beyond. Notably, if the samples are drawn with replacement, an infinite number of samples can be derived from the population.
Properties of the Sampling Distribution of the Mean
- Unbiasedness: The mean of the sampling distribution equals the population mean.
- Efficiency: The sample mean tends to approach the population mean more closely than any other unbiased estimator.
- Consistency: As the sample size increases, the variability of the sample mean from the population mean decreases.
Applications of Sampling Distribution
- Sampling distributions, such as the normal distribution, serve as descriptive models and are utilized to depict real-world scenarios.
- They are invaluable for making probabilistic statements about specific observations.
- Investigators, researchers, and modelers employ sampling distributions for estimation and hypothesis testing.
Conclusion
Sampling involves selecting observations from a larger group or population. The sampling distribution is characterized as the frequency distribution of a statistic across numerous samples. Specifically, it pertains to the distribution of means and is often referred to as the sampling distribution of the mean. This theoretical distribution of a sample statistic varies depending on the specific statistic being analyzed and is characterized by parameters, including µ (the population mean) and σ (the standard error). Notably, the sampling distribution of the mean is a special case within the broader context of sampling distributions.
FAQs on Sampling Distributions - Management Optional Notes for UPSC
| 1. What are the properties of the sampling distribution of the mean? |  |
| 2. What are some applications of the sampling distribution? |  |
| 3. What is the mean of the sampling distribution of the mean? |  |
| 4. How does the sample size affect the sampling distribution of the mean? |  |
| 5. What is the standard deviation of the sampling distribution of the mean? |  |



















