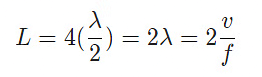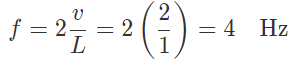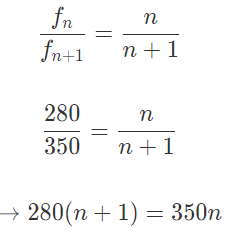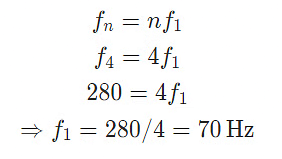Standing Waves, Normal Modes & Beats | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Standing Waves |

|
| Stretched String fixed at Both Ends |

|
| Air Column with One End Closed |

|
| Beats |

|
Standing Waves
In certain situations, like a string fixed at both ends or an air column in a closed pipe, waves can bounce back and forth multiple times, creating what we call standing waves or stationary waves. Imagine a wave traveling in one direction along a string, reflecting at one end, then bouncing back from the other end. This process repeats until a steady wave pattern forms on the string.
- Mathematically, when we consider a wave moving in the positive x-direction and its reflection with the same amplitude and wavelength in the negative x-direction, we get a resultant wave described by the equation y(x, t) = 2a sin(kx)cos(ωt).
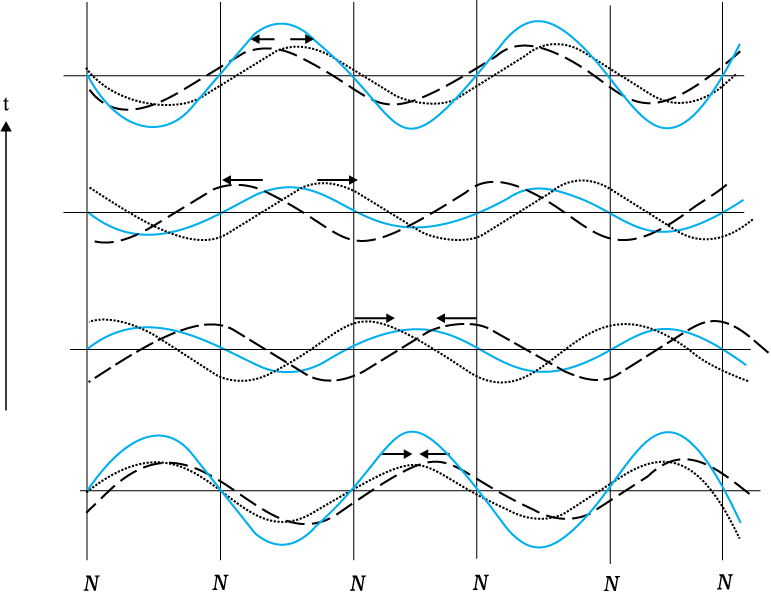 Stationary Waves Arising from Superposition
Stationary Waves Arising from Superposition
- This wave pattern is different from a regular traveling wave because the terms kx and ωt appear separately, not combined. The amplitude varies from point to point along the string, but each element of the string oscillates with the same frequency. This type of wave doesn't move left or right; it stands still, hence the name "standing" or "stationary" waves.
- In standing waves, the amplitude is fixed at a specific location, but it varies at different points.
- Nodes are points where there is no motion, and antinodes are points with the largest amplitude.
- The system of standing waves is limited by boundary conditions, meaning it has specific wavelengths or frequencies it can oscillate with. These are called natural frequencies or normal modes of oscillation.
- For example, a stretched string fixed at both ends follows these constraints in its vibration patterns.
Nodes
The positions of nodes (where the amplitude is zero) in a standing wave are given by the condition sin(kx) = 0 , implying kx = nπ where ( n = 0, 1, 2, 3, .....).
Since k = 2π/λ, we get x = nλ/2 , where n = 0, 1, 2, 3, .....
The distance between any two consecutive nodes is λ/2.
Antinodes
Similarly, the positions of antinodes (where the amplitude is largest) are given by the condition
|sin(kx)|= 1 , implying kx = (n + 1/2)π where ( n = 0, 1, 2, 3, .....).
With k = 2π/λ, we get x = (n+1/2)λ/2, where ( n = 0, 1, 2, 3, .....).
The distance between any two consecutive antinodes is λ/2.
Stretched String fixed at Both Ends
For a stretched string fixed at both ends, Taking one end to be at x = 0, the boundary conditions are that x = 0 and x = L are positions of nodes. The x = 0 condition is already satisfied.
- The x = L node condition requires that the length L is related to λ by L = nλ/2, where ( n = 0, 1, 2, 3, .....).
- This constraint results in possible wavelengths for stationary waves given by λ = 2L/n, where ( n = 0, 1, 2, 3, .....), with corresponding frequencies v = nv/2L for ( n = 0, 1, 2, 3, .....).
- These frequencies correspond to normal modes of oscillation, where the lowest frequency (n = 1) is called the fundamental mode or first harmonic, For the stretched string fixed at either end it is given by v = v/2L , . Higher frequencies (n = 2, 3, ...) are termed the second harmonic, third harmonic, and so on.
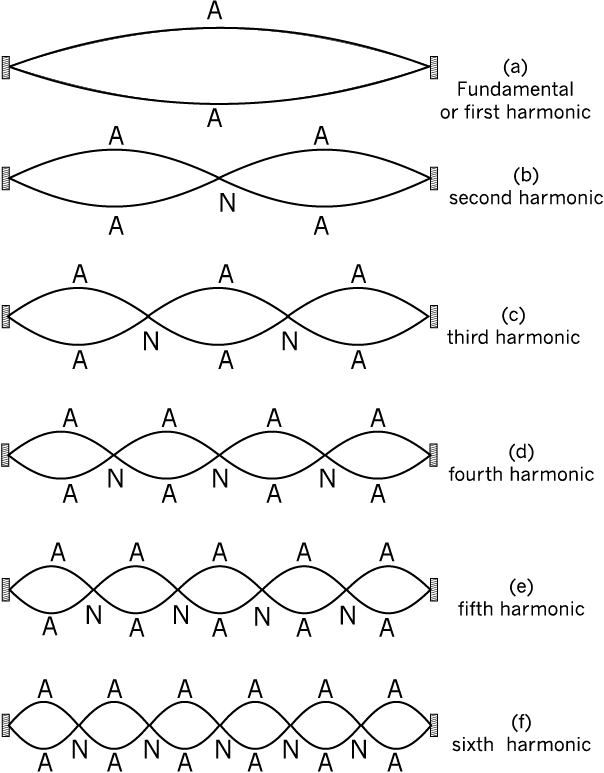 The First six harmonics of a Stretched String Fixed at Both Ends
The First six harmonics of a Stretched String Fixed at Both Ends
Musical instruments, like sitars or violins, use these principles, producing a superposition of different modes when plucked or bowed. The illustration in Figure 15.13 depicts the first six harmonics of a stretched string fixed at both ends.
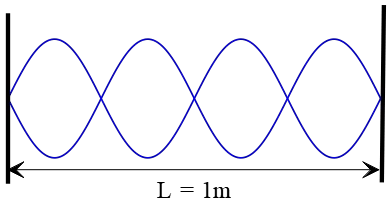
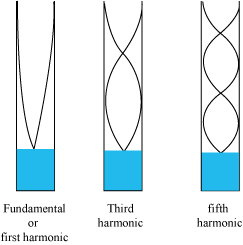
Example 1: The standing wave pattern is observed in a stretched string fixed at both ends, as shown in the figure below. If the speed of the waves in the string is 2m/s, at what frequency is this standing wave vibrating?
Answer: In the standing wave pattern shown, there are four loops or antinodes. These loops fit into the length of the string L. On the other side, recall that each loop has a length of ℓ=. So, the whole length of this string can accommodate four of these loops i.e. L=4ℓ or L=4(λ/2).
The wave speed and wavelength are also related together by λ=v/f. Substituting this into the length formula above, we get
Rearranging this relation and putting the numerical values, the required frequency is obtained as
Example 2: Two successive overtones of a vibrating guitar string are 280Hz and 350Hz. Find the frequency of the first harmonic?
Solution: Overtone is a name for other frequencies except the fundamental frequency. Suppose fn=280Hz, where n is not equal to 1, to be an unknown overtone. The next overtone after this is obtained by increasing n by one as n->n+1. So, the other next overtone is fn+1=350Hz.
Standing wave formula relates the other overtones to the first harmonic or fundamental frequency as fn=nf1. Divide those two overtones by each other and solve for n.
Solving the above equation, gets
This indicates that this particular standing wave formed on the string has four antinode or four loops.
Using the value of one of the given above overtone and substitute n=4 into it, we can find the fundamental frequency, f1.
Hence, the frequency of the first harmonic is 70Hz.
Air Column with One End Closed
Let's now consider the normal modes of oscillation for an air column with one end closed and the other open, such as a partially filled glass tube. In this system, the end in contact with water serves as a node (maximum pressure change, zero displacement), while the open end acts as an antinode (least pressure change, maximum displacement).
- Assuming the end in contact with water is at x = 0, the node condition is already satisfied. If the other end at x = L is an antinode, the equation L = (n+1/2)λ , where ( n = 0, 1, 2, 3, .....), gives the possible wavelengths: λ = 2L/2n + 1 for ( n = 0, 1, 2, 3, .....).
- The natural frequencies (normal modes) of the system are given by v = (n + 1/2)v/L for ( n = 0, 1, 2, 3, .....).
- The fundamental frequency corresponds to n = 0, given by v = v/4L. The higher frequencies are odd harmonics, i.e., odd multiples of the fundamental frequency: 3v/4L, 5v/4L and so on.
 Normal Modes of an Air Column Open at One End and Closed at Other
Normal Modes of an Air Column Open at One End and Closed at Other
For a pipe open at both ends, both ends act as antinodes, producing all harmonics.
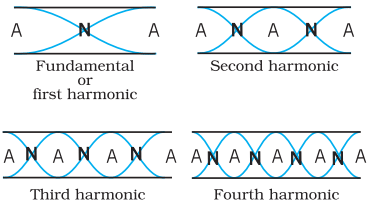 Standing Waves in an Open Pipe
Standing Waves in an Open Pipe
Both string and air column systems can also experience forced oscillations. When an external frequency is close to one of the natural frequencies, the system exhibits resonance.
In the case of a circular membrane, like a tabla, the normal modes are determined by the condition that no point on the membrane's circumference vibrates. Estimating the frequencies of these modes is more complex, involving wave propagation in two dimensions, although the underlying physics remains the same.
Beats
'Beats' is an interesting thing that happens when two sound waves with similar but not exactly equal frequencies overlap.
- When we hear these waves together, we perceive a sound with an average frequency.
- However, we also hear a noticeable increase and decrease in the loudness of the sound, happening at a frequency equal to the difference between the two close frequencies.
- Musicians use this phenomenon to tune their instruments. They adjust until they can't hear these variations anymore.
- To explain this mathematically, let's consider two sound waves with slightly different frequencies, ω1 and ω2. When combined, they create a resultant wave with an average frequency ωa and a changing amplitude.
- This changing amplitude causes the sound to vary in intensity, creating a beat frequency of 2(ωa - ωb), where ωb is half the difference between ω1 and ω2.
- In simpler terms, the beat frequency (νbeat) is equal to the difference in the frequencies of the two waves.
- In an example with frequencies 11 Hz and 9 Hz, the resultant wave shows beats at a frequency of 2 Hz, meaning the loudness of the sound varies at a rate of 2 times per second.
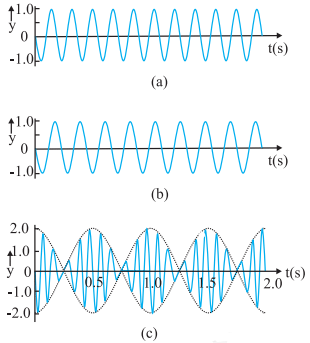 Superposition of 11Hz and 9Hz Harmonic Waves
Superposition of 11Hz and 9Hz Harmonic Waves
Example 3: Find the beat frequency when two waves have frequencies of 550Hz and 380Hz.
Answer: With frequencies f1 = 550Hz and f2 = 380Hz,
The beat frequency (fb) is calculated as the absolute difference between the two frequencies: |380 - 550| = 170Hz.
Therefore, the beat frequency is 170Hz.
|
96 videos|367 docs|98 tests
|
FAQs on Standing Waves, Normal Modes & Beats - Physics Class 11 - NEET
| 1. What are standing waves and how are they formed in a stretched string fixed at both ends? |  |
| 2. How are standing waves produced in an air column with one end closed? |  |
| 3. What are normal modes in the context of standing waves and how are they related to the frequency of the waves? |  |
| 4. How do beats occur in the context of standing waves and how are they used in music tuning? |  |
| 5. How can the concept of standing waves be applied in real-life scenarios outside of academic contexts? |  |