Surface Area and Volume of Cube, Cuboid & Cylinder | Mathematics (Maths) Class 8 PDF Download
In our daily life, we see many objects like books, pencil boxes, cones, football, cylinder. These all are three-dimensional objects (solid shapes). All these objects occupy some shape and have three dimensions Length, Breadth, Height, or Depth. We often find some shapes with two or more identical (congruent) faces. For example, the cube has squared faces on each side.
Surface Area
- The surface area of an object is the sum of the areas of all the shapes that cover its surface.
- For example, a cube is made up of six square faces. If each side of the cube is of length 'a', then:
- The area of one face is a².
- The total area of all six faces is 6a², which is the surface area of the cube.
Cube
- A cube is a type of three-dimensional box with six equal square faces.
- Each face of the cube meets the adjacent faces at a right angle, which is 90 degrees.
- At each corner of the cube, three sides meet at the same point, known as a vertex.
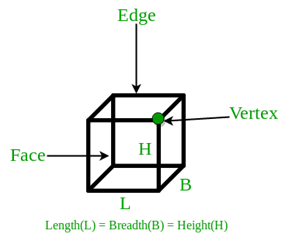
We know that the cube consists of 6 square faces. Let us consider, if each side of a cube is a, then the,
The total surface area of the cube is 6a2
Length of Edge of Cube
From the surface area of the cube, we can find the length of the edge of the cube by rearranging the formula,
Area = 6 * side2
=> side2 = Area / 6
=> side = √Area / 6
Examples
Example 1. If the sidewall of a cubic structure is 5m, then find the Total Surface Area
Solution: Given, length of sidewall = 5m
Total surface Area = 6a2
= 6 (52)
= 6 (25)
= 150 sq.m
Example 2. Find the length of the edge of the cube, if its Area is 294 sq.m?
Solution:
Given, Area = 294 sq.m
Length of edge of cube = √ Area / 6
= √ (294 / 6)
= √ 49
= 7 m
Example 3. What is the surface area of a cube of side 6cm?
Solution:
Given,
Side of cube = a = 6cm
Surface Area of cube = 6a2
= 6 * 62 cm2
= 216 cm2
Example 4. Find the side of a cube whose surface area is 384 cm2?
Solution:
Given,
Surface area of a cube = 384 cm2
Let ‘a’ be the side of a cube .
we know that , surface area of cube = 6a2
=> 6a2 = 384
=> a2 = 384 / 6
=> a2 = 64
=> a = √64
=> a = 8
Therefore, side of a cube = 8cm.
Note: The lateral surface area of a cube is the Total surface area of a cube, which is equal to the sum of areas of all its sides.
Cuboid
A cuboid is made up of six rectangular planes, with different values of length, width, and height. It may be a brick or a box which has a rectangular view from aside. A cuboid is a three-dimensional solid with six rectangular faces. It has 8 vertices and 12 edges. The opposite faces of cuboids are always equal.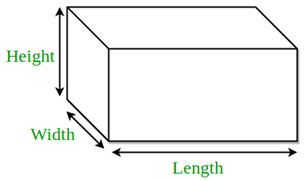
A cuboid has three measures Total surface area, Lateral surface area, and volume. The surface areas are measured in square units.
Total Surface Area of a Cuboid
The Total Surface Area of a cuboid is the sum of its 6 rectangular faces, given by
2 (lw + wh + lh)
l = length, w = width, h = height
Lateral Surface Area of a Cuboid
The Lateral Surface Area of a cuboid is the sum of its 4 rectangular faces leaving its base and top.
LSA = 2 (lh + wh)
= 2h (l + w) sq.units
Examples
Example 1. Find the total surface area of a cuboid having dimensions as length = 4cm , width = 3cm , height = 2cm?
Solution:
Given h = 2cm, l = 4cm, w = 3cm
TSA = 2 (lw + wh + hl)
= 2 (4 * 3 + 3 * 2 + 2 * 4)
= 2 (12 + 6 + 8)
= 2 (26)cm2
= 52 cm2
Example 2. Find the Lateral Surface area of the cuboid, if its length, breadth, and height are 8cm, 9cm, and 10cm respectively?
Solution:
Given length = 8cm
breadth = 9cm, height = 10cm
Lateral Surface Area = 2h (l + b)
= 2 * 10 (8 + 9)
= 2 * 10 (17)
= 2 * 170 cm2
= 340 cm2
Example 3. Find the Total and Lateral Surface Areas of the cuboid with the following dimensions?
Length = 4cm
width = 5cm
height = 6cm
Solution:
Total Surface Area = 2 (lw + wh + lh)
= 2 (4 * 5 + 5 * 6 + 4 * 6)
= 2 (20 + 30 + 24)
= 2 (74)
= 148 sq.cm
Lateral Surface Area = 2h (l + w)
= 2 * 6 (4 + 5)
= 12 (9)
= 108 cm2
Cylinder
A cylinder is a three-dimensional object with two circular bases parallel to each other. Cylinder is a curved surface with two circular bases.
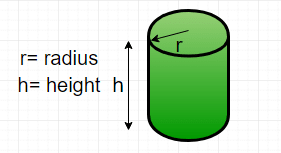
- Curved Surface Area of Cylinder = 2π * r * h sq.units,
- Area of two circular bases = 2 (πr2)
The Total Surface Area of a cylinder is the area occupied by its surface in three-dimensional space. It is defined as the sum of the area of curved surfaces and the Area of circular bases.
Total Surface Area of Cylinder = 2π * r * h + 2 (πr2)
= 2πr (h + r)
Where:
r = radius of cylinder
h = height of cylinder
π = 3.14 or 22/7
Examples
Example 1. Find the curved surface area of the cylinder with a diameter of 6cm and a height of 4cm?
Solution:
Given,
diameter = 6cm , radius = 3cm, height = 4cm
Curved Surface Area = 2π * r * h Square Units.
= 2 * 3.14 * 3 * 4
= 75.36 cm2
Example 2. Calculate the cost required to paint a container that is in the shape of a cylinder having a base radius of 10cm and height of 15 cm. If the painting cost of the container is INR 3 / cm2?
Solution:
Given, Radius of container = 10cm
Height = 15cm
Total Surface Area of container = 2πr (h + r)
= 2 * 3.14 * 10 (15 + 10)
= 2 * 3.14 * 10 (25)
= 1570 cm2
Painting cost per 1cm2 = Rs. 3
Total cost of painting the container = 3 * 1570
= Rs.4710
Example 3. Find the total surface area and curved surface area of a cylinder with a diameter of 12cm and height of 10cm.
Solution:
Given,
diameter = 12cm, radius = 6cm
height = 10cm
Total Surface Area = 2πr (h + r)
= 2 * 3.14 * 6 (10 + 6)
= 602.88 sq.cm
Curved Surface Area = 2π * r * h
= 2π * 6 * 10
= 376.8 sq.cm
Example 4. If the lateral Surface Area of a cylinder is 484 cm2 and its height is 12 cm, then find its radius of the base?
Solution:
Given,
Lateral Surface Area of cylinder = 484
2π * r * h = 484
2 * 3.14 * r * 12 = 484
75.36 * r = 484
r = 484 / 75.36
r = 6.42
Therefore the radius of the cylinder is 6.42 cm.
Mensuration the branch of mathematics which deals with the study of different geometrical shapes, their areas, and volume. It uses geometric calculations and algebraic equations to compute the measurement of various aspects of objects like Surface Area, Volume, etc.
Volume is the measurement of the amount of space inside a 3D object that can be filled. It can be the measurement of any solid objects like cube, square, cylinder, sphere, pyramid, etc. Volume of an object is usually measured using cubic units. By finding out the volume of an object it also helps us find the amount required to fill an object The S.I unit of volume is m3. Other units are ml/L.
1m3 = 1 Litre
Computing Volumes of 3D Objects
Till now you must have understood the meaning of volume, let’s move to finding the volume of various 3D geometrical figures like cube, cuboid, and cylinder.
Finding Volume of a Cuboid
A cuboid is a three-dimensional structure having six rectangular faces. The volume of a cuboid is equal to the product of length, breadth, and height of the cuboid. In rectangular cuboid, all the angles are at right angles and the opposite faces of a cuboid are equal.
Let l is the length, b is the breadth and h is the height of the cuboid.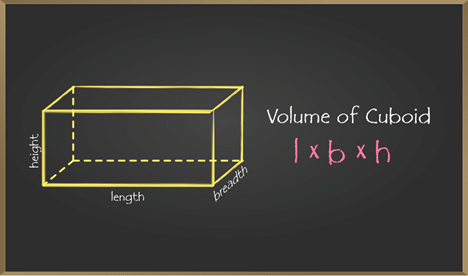
Example 1. Calculate the volume of the cuboid where length, breadth, and height are 12, 8, and 4 meters respectively.
Solution: Given, Length=12m
Breadth = 8m
Height = 4m
Applying the Formula,
Volume of cuboid = length x breadth x height
Volume of cuboid = 12 x 8 x 4 = 384m3
Example 2. Calculate the breadth of the cuboid whose volume is given as 350-meter cube. And length and height are 7 and 5 meters respectively.
Solution: Given Volume of cuboid = length x breadth x height
350 = 7 x breadth x 5
350/35 = breadth
10m = breadth
Volume of a Cube
Firstly the question arises what is cube? So, Cube is a three-dimensional shape with equal width, height, and length measurements. Basically, a cuboid whose length, width, and height are equal is called a cube.
Since we know the volume of cuboid = length x breadth x height and the cube is a special case of cuboid where all length, breadth, and height are equal. Let’s assume length = breadth = height = a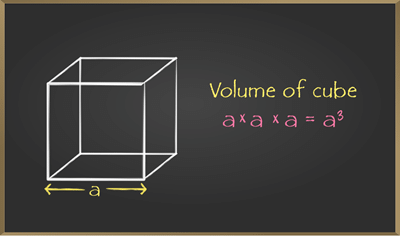
Example 1: Find the volume of a cube with sides of length 10 cm.
Solution: We know, V = (a3)
V = (103 cm)
So, Volume of cube = 1000 centimetre cube
Example 2: Find the length of the sides of the cube whose volume is 343 centimetre cube
Solution : Volume = side x side x side
343= (side)3
7 cm = side
Volume of Cylinder
A cylinder is a three-dimensional solid that contains two parallel bases connected by a curved surface. The bases are usually circular in shape. The perpendicular distance between the bases is denoted as the height “h” of the cylinder and “r” is the radius of the cylinder.
Example 1. Calculate the volume of the cylindrical container having a radius of 4 cm and height of 35 cm.
(Take π = 22/7)
Solution: Radius = 4cm
Height = 35cm
Putting the values in the formulae,
Volume of cylinder = π x 4 x 4 x 35
= π x 560 (π = 22/7)
= 1760 cm3
Example 2. Calculate the radius of the cylinder whose height is 21 cm and volume of the cylinder is 1100 centimetre cube?(Take π = 22/7)
Solution: Volume of cylinder = πr2h cubic units
1100 = 22/7 x r x r x 21
r = 4.08cm
|
81 videos|423 docs|31 tests
|
FAQs on Surface Area and Volume of Cube, Cuboid & Cylinder - Mathematics (Maths) Class 8
| 1. How do you find the surface area of a cube? |  |
| 2. What is the formula for finding the volume of a cuboid? |  |
| 3. How can we determine the surface area of a cylinder? |  |
| 4. What is the difference between volume and surface area? |  |
| 5. How can we find the volume of a cube if its surface area is given? |  |
















