The Potential Step | Physics Optional Notes for UPSC PDF Download
Another simple problem consists of a particle that is free everywhere, but beyond a particular point, say x = 0, the potential increases sharply (i.e., it becomes repulsive or attractive). A potential of this type is called a potential step:

In this problem we try to analyze the dynamics of a flux of particles (all having the same mass m and moving with the same velocity) moving from left to the right. We are going to consider two cases, depending on whether the energy of the particles is larger or smaller than V0.
(a) Case E > V0
The particles are free for x < 0 and feel a repulsive potential V0 that starts at x = 0 and stays flat (constant) for x > 0. Let us analyze the dynamics of this flux of particles classically and then quantum mechanically.
Classically, the particles approach the potential step or barrier from the left with a constant momentum 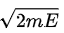 . As the particles enter the region x ≥ 0, where the potential now is V = V0, they slow down to a momentum
. As the particles enter the region x ≥ 0, where the potential now is V = V0, they slow down to a momentum 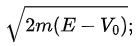 they will then conserve this momentum as they travel to the right. Since the particles have sufficient energy to penetrate into the region x ≥ 0, there will be total transmission: all the particles will emerge to the right with a smaller kinetic energy E - V0. This is then a simple scattering problem in one dimension.
they will then conserve this momentum as they travel to the right. Since the particles have sufficient energy to penetrate into the region x ≥ 0, there will be total transmission: all the particles will emerge to the right with a smaller kinetic energy E - V0. This is then a simple scattering problem in one dimension.
Quantum mechanically, the dynamics of the particle is regulated by the Schrödinger equation, which is given in these two regions by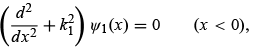
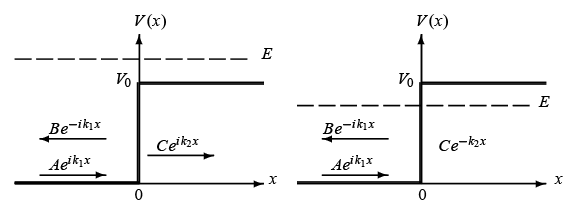
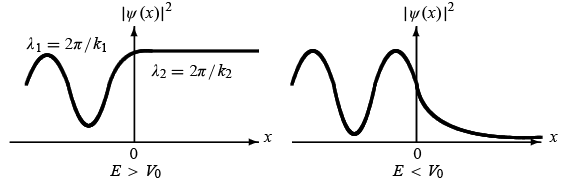
Potential step and propagation directions of the incident, reflected, and transmitted waves, plus their probability densities |ψ(x)|² when E > V₀ and E < V₀.
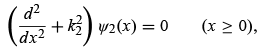
where 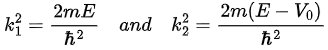 . The most general solutions to these two equations are plane waves:
. The most general solutions to these two equations are plane waves:

where 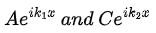 represent waves moving in the positive x-direction, but
represent waves moving in the positive x-direction, but 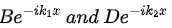 correspond to waves moving in the negative x-direction. We are interested in the case where the particles are initially incident on the potential step from the left: they can be reflected or transmitted at x = 0 . Since no wave is reflected from the region x > 0 to the left, the constant D must vanish. Since we are dealing with stationary states, the complete wave function is thus given by
correspond to waves moving in the negative x-direction. We are interested in the case where the particles are initially incident on the potential step from the left: they can be reflected or transmitted at x = 0 . Since no wave is reflected from the region x > 0 to the left, the constant D must vanish. Since we are dealing with stationary states, the complete wave function is thus given by
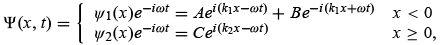
where 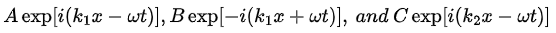 represent the incident, the reflected, and the transmitted waves, respectively; they travel to the right, the left, and the right. Note that the probability density |ψ(x)|² shown in the lower left plot of Figure 4.2 is a straight line for x > 0 , since
represent the incident, the reflected, and the transmitted waves, respectively; they travel to the right, the left, and the right. Note that the probability density |ψ(x)|² shown in the lower left plot of Figure 4.2 is a straight line for x > 0 , since 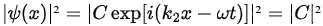 .
.
Let us now evaluate the reflection and transmission coefficients, R and T, as defined by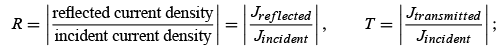
R represents the ratio of the reflected to the incident beams and T the ratio of the transmitted to the incident beams. To calculate R and T, we need to find Jincident, Jreflected and Jtransmitted. Since the incident wave is 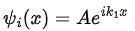 , the incident current density (or incident flux) is given by
, the incident current density (or incident flux) is given by
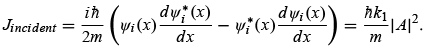
Similarly, since the reflected and transmitted waves are 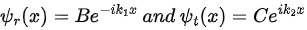 , we can verify that the reflected and transmitted fluxes are
, we can verify that the reflected and transmitted fluxes are

A combination of (4.20) to (4.22) yields

Thus, the calculation of R and T is reduced to determining the constants B and C. For this, we need to use the boundary conditions of the wave function at x = 0 . Since both the wave function and its first derivative are continuous at x = 0 ,
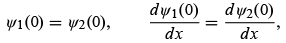
equations (4.17) and (4.18) yield
A + B = C, k1 (A - B) = k2 C;
hence
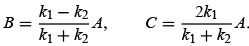
As for the constant A, it can be determined from the normalization condition of the wave function, but we don't need it here, since R and T are expressed in terms of ratios. A combination of above equations leads to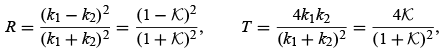
where 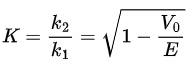 . The sum of R and T is equal to 1, as it should be.
. The sum of R and T is equal to 1, as it should be.
In contrast to classical mechanics, which states that none of the particles get reflected, equation (4.27) shows that the quantum mechanical reflection coefficient R is not zero: there are particles that get reflected in spite of their energies being higher than the step V0. This effect must be attributed to the wavelike behavior of the particles.
From (4.27) we see that as E gets smaller and smaller, T also gets smaller and smaller so that when E = V0 , the transmission coefficient T becomes zero and R = 1 . On the other hand, when 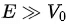 , we have
, we have 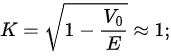 hence R = 0 and T = 1 . This is expected since, when the incident particles have very high energies, the potential step is so weak that it produces no noticeable effect on their motion.
hence R = 0 and T = 1 . This is expected since, when the incident particles have very high energies, the potential step is so weak that it produces no noticeable effect on their motion.
Remark: physical meaning of the boundary conditions
Throughout this chapter, we will encounter at numerous times the use of the boundary conditions of the wave function and its first derivative. What is the underlying physics behind these continuity conditions? We can make two observations:
- Since the probability density
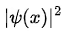 of finding the particle in any small region varies continuously from one point to another, the wave function Ψ(x) must, therefore, be a continuous function of x; thus, we must have
of finding the particle in any small region varies continuously from one point to another, the wave function Ψ(x) must, therefore, be a continuous function of x; thus, we must have 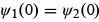 .
. - Since the linear momentum of the particle,
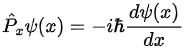 , must be a continuous function of x as the particle moves from left to right, the first derivative of the wave function, d Ψ(x)/dx, must also be a continuous function of x , notably at x = 0. Hence, we must have
, must be a continuous function of x as the particle moves from left to right, the first derivative of the wave function, d Ψ(x)/dx, must also be a continuous function of x , notably at x = 0. Hence, we must have 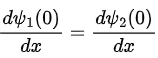 .
.
(b) Case E < V_0
Classically, the particles arriving at the potential step from the left (with momenta  ) will come to a stop at x = 0 and then will bounce back to the left with the magnitudes of their momenta unchanged. None of the particles will make it into the right side of the barrier x = 0 ; there is total reflection of the particles. So the motion of the particles is reversed by the potential barrier.
) will come to a stop at x = 0 and then will bounce back to the left with the magnitudes of their momenta unchanged. None of the particles will make it into the right side of the barrier x = 0 ; there is total reflection of the particles. So the motion of the particles is reversed by the potential barrier.
Quantum mechanically, the picture will be somewhat different. In this case, the Schrödinger equation and the wave function in the region x < 0 are given by (4.15) and (4.17), respectively. But for x > 0 the Schrödinger equation is given by
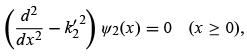
where 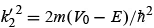 . This equation’s solution is
. This equation’s solution is
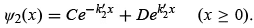
Since the wave function must be finite everywhere, and since the term 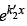 diverges when x→ ∞, the constant D has to be zero. Thus, the complete wave function is
diverges when x→ ∞, the constant D has to be zero. Thus, the complete wave function is
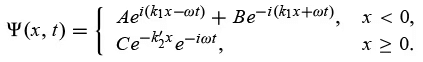
Let us now evaluate, as we did in the previous case, the reflected and the transmitted coefficients. First we should note that the transmitted coefficient, which corresponds to the transmitted wave function 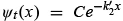 is zero since Ψt(x) is a purely real function
is zero since Ψt(x) is a purely real function 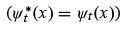 and therefore
and therefore
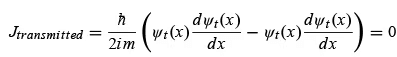 Hence, the reflected coefficient R must be equal to 1. We can obtain this result by applying the continuity conditions at x= 0 for (4.17) and (4.29):
Hence, the reflected coefficient R must be equal to 1. We can obtain this result by applying the continuity conditions at x= 0 for (4.17) and (4.29): Thus, the reflected coefficient is given by
Thus, the reflected coefficient is given by We therefore have total reflection, as in the classical case.There is, however, a difference with the classical case: while none of the particles can be found classically in the region x > 0, quantum mechanically there is a nonzero probability that the wave function penetrates this classically forbidden region. To see this, note that the relative probability density
We therefore have total reflection, as in the classical case.There is, however, a difference with the classical case: while none of the particles can be found classically in the region x > 0, quantum mechanically there is a nonzero probability that the wave function penetrates this classically forbidden region. To see this, note that the relative probability density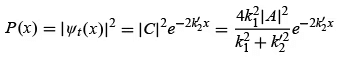 is appreciable near x =0 and falls exponentially to small values as x becomes large; the behavior of the probability density is shown in Figure 4.2.
is appreciable near x =0 and falls exponentially to small values as x becomes large; the behavior of the probability density is shown in Figure 4.2.
The Potential Barrier and Well
Consider a beam of particles of mass m that are sent from the left on a potential barrier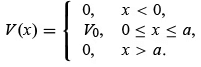 This potential, which is repulsive, supports no bound states (Figure 4.3). We are dealing here, as in the case of the potential step, with a one-dimensional scattering problem.Again, let us consider the following two cases which correspond to the particle energies being respectively larger and smaller than the potential barrier.
This potential, which is repulsive, supports no bound states (Figure 4.3). We are dealing here, as in the case of the potential step, with a one-dimensional scattering problem.Again, let us consider the following two cases which correspond to the particle energies being respectively larger and smaller than the potential barrier.
The Case E > V0
Classically, the particles that approach the barrier from the left at constant momentum, 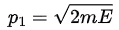 , as they enter the region 0 ≤ x ≤ a will slow down to a momentum
, as they enter the region 0 ≤ x ≤ a will slow down to a momentum 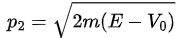 . They will maintain the momentum p_2 until they reach the point x = a . Then, as soon as they pass beyond the point x = a , they will accelerate to a momentum
. They will maintain the momentum p_2 until they reach the point x = a . Then, as soon as they pass beyond the point x = a , they will accelerate to a momentum 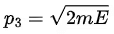 and maintain this value in the entire region x > a . Since the particles have enough energy to cross the barrier, none of the particles will be reflected back; all the particles will emerge on the right side of x = a : total transmission.
and maintain this value in the entire region x > a . Since the particles have enough energy to cross the barrier, none of the particles will be reflected back; all the particles will emerge on the right side of x = a : total transmission.
It is easy to infer the quantum mechanical study from the treatment of the potential step presented in the previous section. We need only to mention that the wave function will display an oscillatory pattern in all three regions; its amplitude reduces every time the particle enters a new region (see Figure 4.3):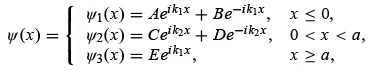
where 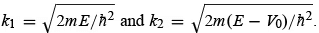 . The constants B, C, D, and E can be obtained in terms of A from the boundary conditions: Ψ (x) and dΨ/dx must be continuous at x = 0 and x = a , respectively:
. The constants B, C, D, and E can be obtained in terms of A from the boundary conditions: Ψ (x) and dΨ/dx must be continuous at x = 0 and x = a , respectively:
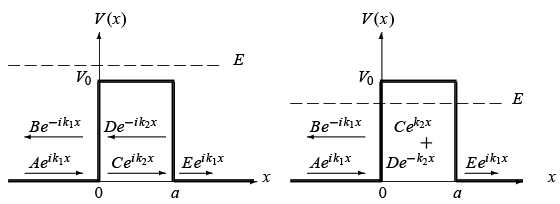
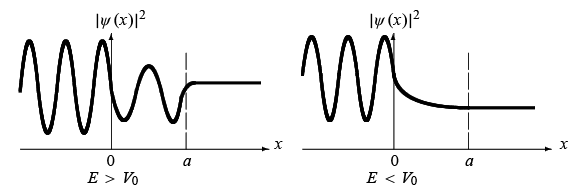 Figure 4.3 Potential barrier and propagation directions of the incident, reflected, and transmitted waves, plus their probability densities Ψ(x)|2 when E > V0 and E < V0.
Figure 4.3 Potential barrier and propagation directions of the incident, reflected, and transmitted waves, plus their probability densities Ψ(x)|2 when E > V0 and E < V0.
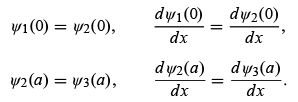 These equations yield
These equations yield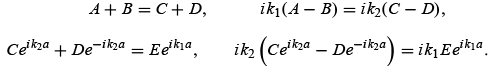 Solving for E, we obtain
Solving for E, we obtain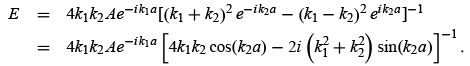 The transmission coefficient is thus given by
The transmission coefficient is thus given by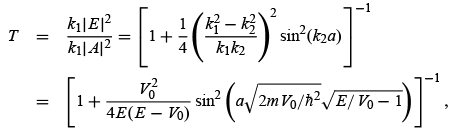
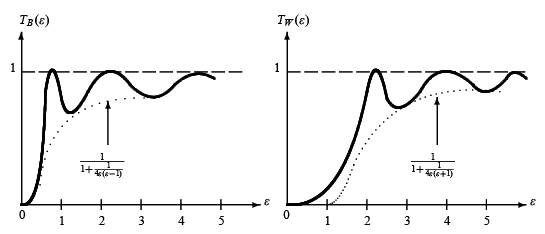
Figure 4.4 Transmission coefficients for a potential barrier, 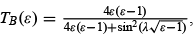 and for a potential well,
and for a potential well, 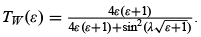
because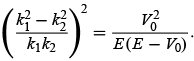
Using the notation 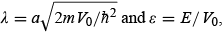 we can rewrite T as
we can rewrite T as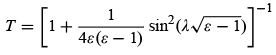 Similarly, we can show that
Similarly, we can show that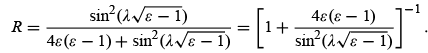
Special cases
If 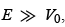 , and hence
, and hence 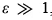 , the transmission coefficient T becomes asymptotically equal to unity,
, the transmission coefficient T becomes asymptotically equal to unity,  . So, at very high energies and weak potential barrier, the particles would not feel the effect of the barrier; we have total transmission.
. So, at very high energies and weak potential barrier, the particles would not feel the effect of the barrier; we have total transmission.
We also have total transmission when 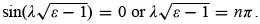 . As shown in Figure 4.4, the total transmission, T(εn) = 1 , occurs whenever
. As shown in Figure 4.4, the total transmission, T(εn) = 1 , occurs whenever 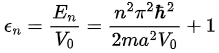 or whenever the incident energy of the particle is
or whenever the incident energy of the particle is 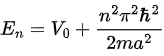 with n = 1, 2, 3, ..... . The maxima of the transmission coefficient coincide with the energy eigenvalues of the infinite square well potential; these are known as resonances. This resonance phenomenon, which does not occur in classical physics, results from a constructive interference between the incident and the reflected waves. This phenomenon is observed experimentally in a number of cases such as when scattering low-energy ( E ∼ 0.1 eV) electrons off noble atoms (known as the Ramsauer–Townsend effect, a consequence of the symmetry of noble atoms) and neutrons off nuclei.
with n = 1, 2, 3, ..... . The maxima of the transmission coefficient coincide with the energy eigenvalues of the infinite square well potential; these are known as resonances. This resonance phenomenon, which does not occur in classical physics, results from a constructive interference between the incident and the reflected waves. This phenomenon is observed experimentally in a number of cases such as when scattering low-energy ( E ∼ 0.1 eV) electrons off noble atoms (known as the Ramsauer–Townsend effect, a consequence of the symmetry of noble atoms) and neutrons off nuclei.
- In the limit ε→1 we have
 , hence (4.44) and (4.45) become
, hence (4.44) and (4.45) become
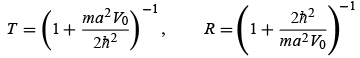
The potential well (V0 < 0)
The transmission coefficient (4.44) was derived for the case where V0 > 0, i.e., for a barrier potential. Following the same procedure that led to (4.44), we can show that the transmission coefficient for a finite potential well, V0 < 0, is given by
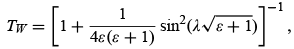
where ε = E/|V0|} and 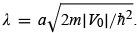 . Notice that there is total transmission whenever
. Notice that there is total transmission whenever 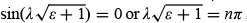 . As shown in Figure 4.4, the total transmission,
. As shown in Figure 4.4, the total transmission, 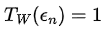 , occurs whenever
, occurs whenever 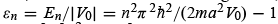 or whenever the incident energy of the particle is
or whenever the incident energy of the particle is 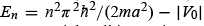 with n = 1, 2, 3,.... . We will study in more detail the symmetric potential well in Section 4.7.
with n = 1, 2, 3,.... . We will study in more detail the symmetric potential well in Section 4.7.
FAQs on The Potential Step - Physics Optional Notes for UPSC
| 1. What is a potential step in the context of UPSC exams? |  |
| 2. How can candidates effectively prepare for the potential step in their UPSC journey? |  |
| 3. What are the common challenges candidates face when approaching the potential step for UPSC? |  |
| 4. Are there specific strategies to overcome obstacles during the potential step for UPSC preparation? |  |
| 5. How important is the potential step in achieving success in the UPSC exams? |  |















