Waves, Wave Motion and Types of Waves | Science & Technology for UPSC CSE PDF Download
You must have heard someone playing a drum or table. The vibrations of a thin membrane produce sound waves. Similarly, in a guitar, the vibration of a stretched string produces sound waves. The origin of every wave is a 'vibration'. Wherever there is a vibration, there will be waves.
In this document, we will study waves in detail.
What is a Wave?
A wave is a vibratory disturbance in a medium which carries energy from one point to another point in a regular and an organised way without any actual movement of the medium.
 A typical Wave
A typical Wave
Wave Motion
- In a wave motion, disturbance travels through some medium, but the medium does not travel with the disturbance.
- We can understand this in the simplest way by considering the example of ripples formed in water when a stone is thrown into it.
- We observe that ripples travel in water in the form of concentric circles of increasing radii. It looks like the water is moving outwards from a point of disturbance as shown in the image below.
- It is actually not the water flowing outwards, rather it is only the disturbance that travels.
 Ripple formation in water
Ripple formation in water
- Similarly, when a drummer beats the drum, the sound is heard at distant points. This means that sound waves carry energy that vibrates the diaphragm of the ear enabling us to hear.
- In this process, air particles vibrate about their mean positions, but they are not transported from one point to another.
Mechanism of Wave Propagation
- The propagation of waves can be understood from the example taken above. When a stone hits a particle of water at O, the particle moves down to A.
- Due to this, restoring force develops towards O, on account of elasticity of water. Work done against the restoring force in moving the particle from 0 to A, is stored in the particle at A in the form of potential energy.
- From A, the particle moves towards O, under the action of restoring force. The potential energy of the particle is converted into kinetic energy at O. On account of inertia, therefore, the particle cannot stop at O.
- It overshoots its mean position O and goes over to B till its entire kinetic energy is converted into potential energy at B.
- From B, the particle moves to O, under the action of restoring force again, and so on.
- Thus the particle of water at O, disturbed once, executes periodic vibrations due to elasticity and inertia.
- This disturbance is communicated to the adjoining particles which also start vibrating simply harmonically about their mean positions. Hence the wave motion travels on and on.

Some Important Terms of Wave Motion
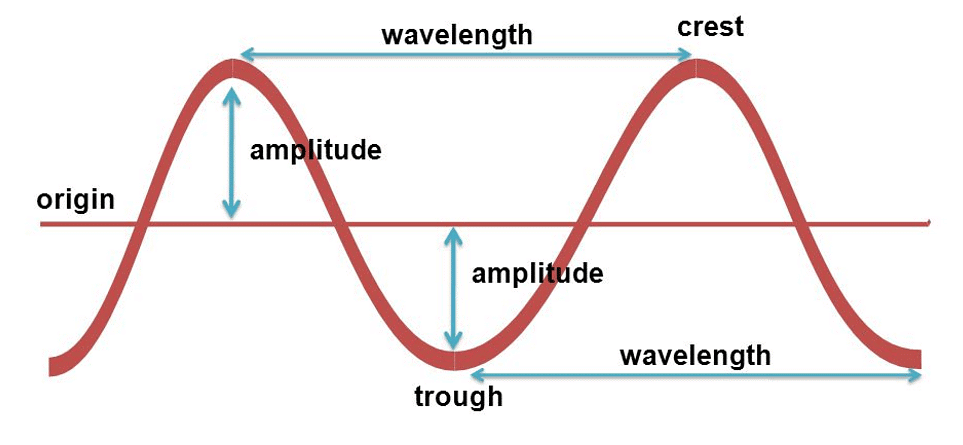 Terms related to waves
Terms related to waves
 Wave Properties
Wave Properties
Types of Waves
There are three types of waves:
- Mechanical Waves: Those waves that require a material medium for their propagation are called mechanical waves, e.g., sound waves, water waves, etc.
- Electromagnetic Waves: Those waves that do not require a material medium for their propagation are called electromagnetic waves, e.g., light waves, radio waves, etc.
- Matter Waves: These waves are commonly used in modern technology but they are unfamiliar to us. These waves are associated with electrons, protons, and other fundamental particles.
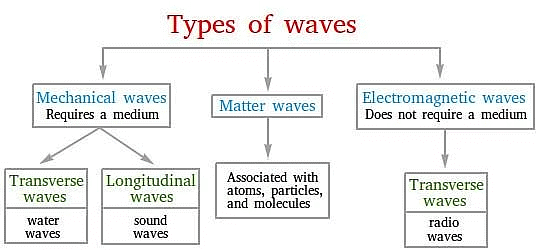 Types of Waves
Types of WavesMechanical Waves
Mechanical waves are waves that require a medium in order to transfer energy away from their source. A medium is matter through which waves can travel.
Three familiar examples of mediums that mechanical waves travel through is air, water, and solid earth. For example, earthquake waves travel through layers within the earth. Sound waves are also mechanical waves that travel through the air, water, and solid matter. Water waves are mechanical waves that move wind energy through water.
Transverse Waves v/s Longitudinal Waves
Transverse waves and longitudinal waves are two main types of mechanical waves, which are disturbances that transfer energy through a medium. The key difference between them lies in the direction of particle displacement and wave propagation.
Here are some differences between Transverse waves and longitudinal waves.
Difference between Transverse and Longitudinal Waves
What are Sound Waves?
Sound waves are a type of mechanical wave that propagates through a medium, typically through air, although they can also travel through other materials like liquids and solids. These waves are the result of vibrations or oscillations of particles within the medium.
Here's how sound waves typically work:
 Sound waves
Sound waves
- Source of Vibration: Sound waves are produced when an object vibrates. This vibration creates a disturbance in the surrounding air molecules.
- Compression and Rarefaction: As the object vibrates, it pushes and pulls air molecules in the surrounding medium. This alternately compresses and rarefies (expands) the air molecules, creating areas of high pressure (compression) and low pressure (rarefaction).
- Propagation: The disturbances in air pressure propagate outward from the vibrating source in the form of waves. These waves travel through the air, carrying the energy of the original vibration.
- Transmission Medium: While we commonly associate sound with air, sound waves can travel through other mediums like water or solids. The speed of sound varies depending on the density and elasticity of the medium.
- Reception: When these waves reach our ears, the pressure variations are detected by the ear's mechanism, and our brain interprets these variations as sound.
Sound Waves are of three types
- Infrasonic Waves: The sound waves of frequency lie between 0 to 20 Hz are called infrasonic waves.
- Audible Waves: The sound waves of frequency lie between 20 Hz to 20000 Hz and are called audible waves.
- Ultrasonic Waves: The sound waves of frequency greater than 20000 Hz are called ultrasonic waves.
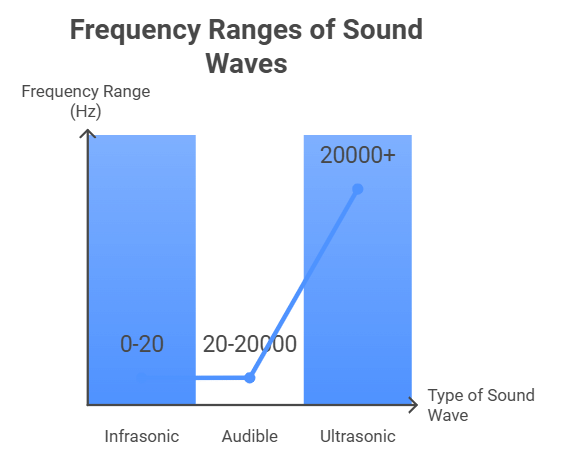
Sound waves are mechanical longitudinal waves and require medium for their propagation.
[sound waves cannot propagate through vacuum.
If Vs, Vi and Vg are speed of sound waves in solid, liquid and gases, then
Vs > Vi > Vg
Sound waves (longitudinal waves) can reflect, refract, interfere and diffract but cannot be polarised as only transverse waves can polarised.
Velocity of Longitudinal (Sound) Waves
The velocity of longitudinal (sound) waves in any medium is given by
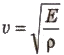
where E is the coefficient of elasticity of the medium and ρ is the density of the medium.
Longitudinal waves
Newton’s Formula
According to Newton, the propagation of longitudinal waves in a gas is an isothermal process. Therefore, the velocity of longitudinal (sound) waves in gas should be
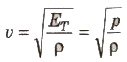
where ET is the isothermal coefficient of volume elasticity and it is equal to the pressure of the gas.
Laplace’s Correction
According to Laplace, the propagation of longitudinal waves is an adiabatic process. Therefore, the velocity of the longitudinal (sound) wave in gas should be
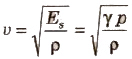
where, ES, is the adiabatic coefficient of volume elasticity and it is equal to γ p.
Factors Affecting Velocity of Longitudinal (Sound) Wave
(a) Effect of Pressure: The formula for velocity of sound in a gas.
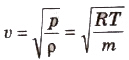
Therefore, (p/ρ) remains constant at a constant temperature.
Hence, there is no effect of pressure on the velocity of the longitudinal wave.
(b) Effect of Temperature: Velocity of longitudinal wave in a gas
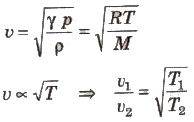
The velocity of sound in a gas is directly proportional to the square root of its absolute temperature.
If v0 and vt are velocities of sound in air at O°C and t°C, then
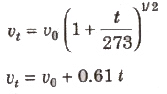
(c) Effect of Density: The velocity of sound in the gaseous medium
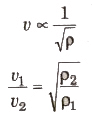
The velocity of sound in a gas is inversely proportional to the square root of the density of the gas.
(d) Effect of Humidity: The velocity of sound increases with an increase in humidity in the air.
Important Questions for Exam
Q.1. If a string wave encounters a completely fixed end, what happens to its phase?
a) Stays the same
b) Changes by π
c) Changes by π/2
d) Waves gets destroyed
Answer: b
Explanation: The reason for the phase to change by π is that the boundary displacement should be zero because it is rigid & by principle of superposition it is only possible if the reflected wave differs by a phase of π.
Q.2. What is the minimum distance between a node & an antinode in a standing wave?
a) λ
b) λ/2
c) 2λ
d) λ/4
Answer: d
Explanation: The amplitude in a standing wave is given by Asin(kx).
Node is a point where amplitude is zero and antinode is a point where amplitude is maximum.
For a node, sin(kx) = 0
kx = 2nπ OR (2π/λ)x = nππ
x = nλ/2.
For an antinode, sin(kx) = 1
kx = (2n+1)π/2
(2π/λ)x = (2n+1)π/2
x = (2n+1) λ/4.
∴ node is at λ/2, λ, 3λ/2 …
& antinode at λ/4, 3λ/4, 5λ/4 …
∴ minimum distance = λ/2 – λ/4 = λ/4.
Q.3. If a standing wave is vibrating in the fourth harmonic and the wavelength is λ, what is the length of the string.
a) 2λ
b) λ
c) 4λ
d) λ/4
Answer: a
Explanation: If the length of string is L, then the wavelength of the standing wave is 2L/n.
Or we can say L = nλ/2, where n corresponds to nth harmonic.
∴ L = 4λ/2
= 2λ.
Q.4. Consider standing waves in an air column with one end closed. What is a pressure node?
a) Pressure variation is maximum
b) Displacement variation is minimum
c) Same as displacement node
d) Least pressure change
Answer: d
Explanation: The point where there is an antinode corresponds to maximum amplitude of displacement. This also implies that here, pressure changes are minimum and it is therefore called a pressure node.
Q.5. A pipe is open at both ends. What should be its length such that it resonates a 10Hz source in the 2nd harmonic? Speed of sound in air = 340m/s.
a) 34m
b) 68m
c) 17m
d) 51m
Answer: a
Explanation: For a pipe open at both ends frequency ‘f’ = nv/2L, where n is speed of sound.
Given: f = 10 & n=2.
∴ 10 = 2*340/2L
∴ L = 680/20
= 34m.
|
90 videos|491 docs|209 tests
|
FAQs on Waves, Wave Motion and Types of Waves - Science & Technology for UPSC CSE
| 1. What is a wave and how is it defined in physics? |  |
| 2. What are the different types of waves based on their motion? |  |
| 3. How does wave propagation occur in different media? |  |
| 4. What factors affect the velocity of sound waves? |  |
| 5. What are some common applications of sound waves in everyday life? |  |






















