Uniform Circular Motion | Physics Class 11 - NEET PDF Download
Circular Motion
Circular motion is described as a movement of an object while rotating along a circular path. Circular motion can be either uniform or non-uniform. During uniform circular motion the angular rate of rotation and speed will be constant while during non-uniform motion the rate of rotation keeps changing.
Some of the most common examples of circular motion include man-made satellite that revolves around the earth, a rotating ceiling fan, a moving car’s wheel, the blades in a windmill, and gears in gas turbines.
A particle is said to execute circular motion when it moves along the circumference of a circular path. An important aspect of circular motion is that the direction of motion is changing continuously unlike in the case of linear motion. Hence circular motion can also be described in terms of angular variables.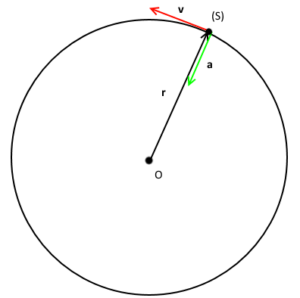
Uniform Circular Motion
This motion refers to the circular motion if the magnitude of the velocity of the particle in circular motion remains constant. The non-uniform circular motion refers to the circular motion when the magnitude of the velocity of the object is not constant. Another special kind of circular motion is when an object rotates around itself also known as spinning motion.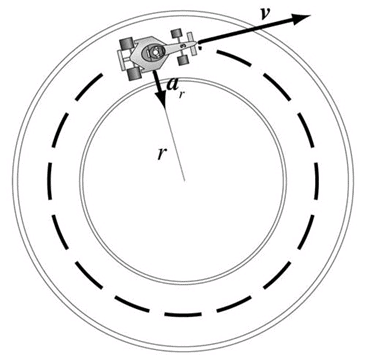 If a particle is moving in a circle, it must have some acceleration acting towards the centre which is making it move around the centre. Since this acceleration is perpendicular to the velocity of a particle at every instant, it is only changing the direction of velocity and not magnitude and that’s why the motion is uniform circular motion. We call this acceleration centripetal acceleration (or radial acceleration), and the force acting towards the centre is called centripetal force.
If a particle is moving in a circle, it must have some acceleration acting towards the centre which is making it move around the centre. Since this acceleration is perpendicular to the velocity of a particle at every instant, it is only changing the direction of velocity and not magnitude and that’s why the motion is uniform circular motion. We call this acceleration centripetal acceleration (or radial acceleration), and the force acting towards the centre is called centripetal force.
In the case of uniform circular motion, the acceleration is:
ar = v2r = ω2r
If the mass of the particle is m, we can say from the second law of motion that:
F = ma
mv2r= mω2r
This is not a special force, actually force like tension or friction may be a cause of origination of centripetal force. When the vehicles turn on the roads, it is the frictional force between tyres and ground that provides the required centripetal force for turning.
Note: So if a particle is moving in a uniform circular motion:
- Its speed is constant
- Velocity is changing at every instant
- There is no tangential acceleration
- Radial (centripetal) acceleration = ω2r
- v = ωr
In case of non-uniform circular motion, there is some tangential acceleration due to which the speed of the particle increases or decreases. The resultant acceleration is the vector sum of radial acceleration and tangential acceleration.
Uniform Circular Motion Examples
Following are the examples of uniform circular motion:
- Motion of artificial satellites around the earth is an example of uniform circular motion. The gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
- The motion of electrons around its nucleus.
- The motion of blades of the windmills.
- The tip of second’s hand of a watch with circular dial shows uniform circular motion.
Variables in Circular Motion
- Angular Displacement: The angle which is subtended by the position vector at the center of the circular path refers to the angular displacement.
Angular Displacement (Δθ) = (ΔS/r)
Where Δ’s refers to the linear displacement while r is the radius. Radian is the unit of Angular Displacement. - Angular Acceleration: It refers to the rate of time of change of angular velocity (dῶ).
Angular acceleration (α) = dῶ/dt = d2θ / dt2
Its unit is rad/s2 and dimensional formula [T]-2. The relation between linear acceleration
(a) and angular acceleration (α)
A = rα, where r is the radius. - Angular Velocity: It refers to the time rate change of angular displacement (dῶ).
Angular Velocity (ῶ) = Δθ/Δt
Angular Velocity is a vector quantity. Its unit is rad/s. The relation between the linear velocity (v) and angular velocity (ῶ) is
v = rῶ - Centripetal Acceleration: It refers to an acceleration that acts on the body in circular motion whose direction is always towards the center of the path.
Centripetal Acceleration (α) = v2/r = rῶ2.
The magnitude of this acceleration by comparing ratios of velocity and position around the circle. Since the particle is traveling in a circular path, the ratio of the change in velocity to velocity will be the same as the ratio of the change in position to position. It is also known as radial acceleration as it acts along the radius of the circle. Centripetal Acceleration is a vector quantity and the unit is in m/s2.
Solved Question for You
Q.1. During the course of a turn, an automobile doubles its speed. How much must additional frictional force the tires provide if the car safely makes around the curve? Since Fc varies with v2, an increase in velocity by a factor of two must be accompanied by an increase in centripetal force by a factor of four.
A satellite is said to be in geosynchronous orbit if it rotates around the earth once every day. For the earth, all satellites in geosynchronous orbit must rotate at a distance of 4.23×107 meters from the earth’s center. What is the magnitude of the acceleration felt by a geosynchronous satellite?
Solution: The acceleration felt by any object in uniform circular motion is given by
a = v2 ÷ r
We are given the radius but must find the velocity of the satellite. We know that in one day, or 86400 seconds, the satellite travels around the earth once. Thus: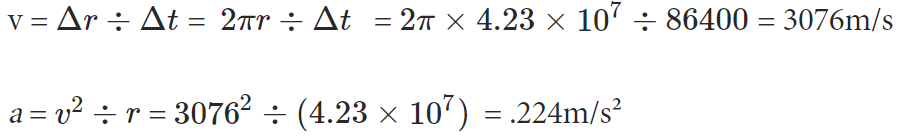
Q.2. A cyclist moves around a circular path of a radius of 50 m with a speed of 10 m/s.
(a) Find the acceleration of the cyclist?
(b) Considering the combined mass of the cyclist and cycle to be 120 kg, what is the net force applied on them?
Solution: (a) A movement with constant speed around a circular path yields a radially inward acceleration called centripetal acceleration whose magnitude is found as below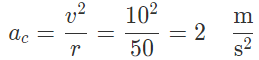
(b) The net force that acts on the object to keep it moving along a circular track is called centripetal force whose magnitude is found using Newton's second law as below
Fnet = mac = 120 × 2 = 240N
Q.3. A race car travelling around a circular path of a radius of 400 m with a speed of 50 m/s. Find the centripetal acceleration of the car.
Solution: In a circular motion with constant speed the centripetal acceleration is ac = v2/r. Therefore, substituting the numerical values into this equation we have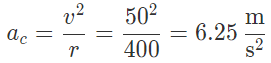
This acceleration is toward the center of the circle.
Q.4. A racer is moving with a constant tangential speed of 50 m/s, takes one lap around a circular track in 40 seconds. Calculate the magnitude of the acceleration of the car.
Solution: Speed v = 50 m/s
T = 40 seconds.
We know that,
Acceleration,
a = v2/r
T = 2 πr/v
Therefore, r = Tv/2π
When both the formulas are combined, we get
a = v2/(Tv/2π) = v/(T/2π)
= 50/[ 40/6.28]
a = 7.86 m/s2
Q.5. An object moving in a circular motion has a centripetal acceleration of 20 m/s2. If the radius of the motion is 0.5 m, calculate the frequency of the motion.
Solution: Given:
Acceleration = 20 m/s2
Radius = 0.5 m
We know that
a = v2/r
20 = v2/0.5
v = 3.16 m/s
v = 2 πr/t
3.16 = (2)(3.14)(0.5)/t
3.16 = 3.14 / t
T = 1.006
Frequency, f = 1/t = 1/1.006
Therefore, f = 0.99 Hz.
|
96 videos|367 docs|98 tests
|
FAQs on Uniform Circular Motion - Physics Class 11 - NEET
| 1. What is circular motion? |  |
| 2. How is uniform circular motion different from non-uniform circular motion? |  |
| 3. What is centripetal force in uniform circular motion? |  |
| 4. Can an object in uniform circular motion have a constant speed but changing velocity? |  |
| 5. What is the relationship between the period and frequency of an object in uniform circular motion? |  |
















