Vapour Pressure, Raoult's Law, Ideal & Non Ideal Solutions | Physical Chemistry for NEET PDF Download
Concept of Vapour Pressure
When a pure liquid is kept in a closed vessel (in which no air is present) the liquid evaporates to give the vapours.
The molecules of the liquid which possess high kinetic energy have a tendency to change to vapour state.
After some time a dynamic equilibrium is established between liquid and vapours.

At Equilibrium
rate of evaporation = rate of condensation.
H2O (ℓ) ⇌ H2O (g)
The pressure that the vapours exert at equilibrium on the walls of the container or on the surface of the liquid is called the vapour pressure of the liquid at that temperature, Figure (a).

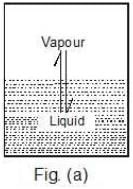
Case 1: What would happen to the vapour pressure of the liquid if we take a bigger container, Figure (b) or a wider container, Figure (c).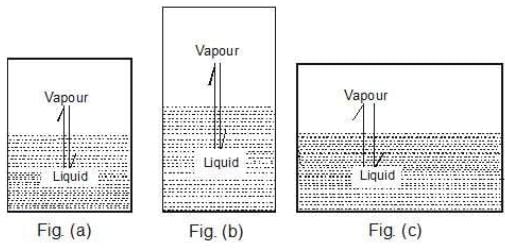
Key concept: When the liquid is in equilibrium with vapours,
Liquid ⇌ Vapours,
the Kp of the system is Kp = Pv,
where Pv is the vapour pressure.
We know that Kp for a given chemical equilibrium is a constant and only depends on temperature. Therefore the vapour pressure of the liquid is a constant and does not depend on the nature of the vessel used and that it only depends on temperature.
Case 2: Take a vessel with the same liquid as in case 1 and cover it with a glass plate (of negligible weight) having a hole in it. Would the vapour pressure be the same now?
Key concept: Well, the liquid system is the same and the temperature is also same. Therefore, the vapour pressure should be same. The vapour pressure of a liquid is independent of the surface area exposed on top of the liquid surface provided the surface area exposed should not be zero.
The vapour pressure of liquid depends upon
- Nature of the liquid
- Temperature
(i) Nature of the Liquid: When the intermolecular forces of attractions are stronger then the vapour pressure will be low because less number of molecules can leave the liquid.
Out of C2H5OH, CH3OCH3, CH3CHO the one with highest vapour pressure is CH3OCH3 and the one with lowest vapour pressure is C2H5OH because in C2H5OH there is hydrogen bonding leading to strongest intermolecular forces where as in CH3OCH3 there is Vander Waals forces leading to weakest intermolecular forces.
Decreasing order of vapour pressure of few liquids is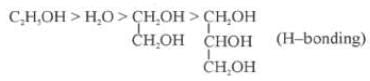
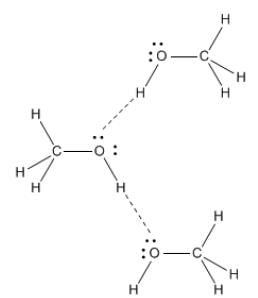
Fig: H-Bonding in Methanol
(ii) Temperature: Higher the temperature, greater would be the vapour pressure.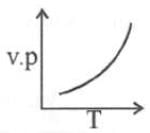
This is because when temperature is raised, kinetic energy of the molecules increase and therefore the number of molecules leaving surface of liquid, is large.
The Clausius Clapeyron equation tells very clearly that as temperature increases the right hand side remains highly and thereby vapour pressure increases.
This equation is,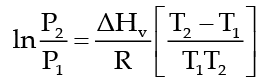
which tells as to how vapour pressure changes with nature of liquid and temperature when vapour pressure is low then the temperature at which the liquid would boil will be high. In the above equation P1 and P2 are vapour pressure of liquid at T1 and T2 respectively, ΔHv, heat of vaporization and R is gas constant.
Vapour Pressure of Liquid Solutions
 Fig: Example of Liquid in Liquid Solution
Fig: Example of Liquid in Liquid Solution
Liquid Solution is formed when we dissolve a solid, liquid or gas in a particular liquid solvent.
Vapour Pressure of liquid solutions is defined as the pressure exerted by the vapours on the liquid solvent when kept in equilibrium and a certain temperature.
- It varies with the nature of liquid and temperature of the surroundings.
Some characteristics of the vapour pressure of liquid solutions are as follows:
- The pure liquid has more vapour pressure as compared to liquid’s solution.
Example: take two beaker one filled with water and other with lemon juice and water, you’ll find that the beaker filled with water has more vapour pressure - Vapour pressure is inversely proportional to forces of attraction between molecules of a liquid
- Vapour pressure increases with increase in temperature, as molecules gain kinetic energy and vapourise briskly

Fig: Vapour pressure equilibrium in different solution
Liquid solution can contain volatile solute and solvent as well. In most cases, the solvent is volatile in nature and the solute left out to be non-volatile.
Vapour pressure can be evaluated in two cases which are:
- Vapour pressure of liquid-liquid solutions that is, solute and solvent both are in liquid phase
- Vapour pressure of solid- liquid solutions that is, solute is in solid state and solvent is in liquid phase
Vapour Pressure of Liquid-Liquid Solutions
To find out vapour pressure of the liquid-liquid solution, we take two volatile liquid solutions and name their liquid component as A and B. When we place the volatile liquid with their components in a closed vessel, we find that equilibrium is established between the liquid phase and vapour phase.
Suppose Ptotal is the overall vapour pressure at an equilibrium state and let PA and PB be the partial vapour pressures of components A and B respectively.
Applying Dalton’s law of partial pressure the total vapour pressure of the solution will be
Psolution = PA + PB
Where PA and PB are the partial vapour pressures of A and B.
Adding further, the mole fraction of respective components is xA and xB respectively.
To evaluate vapour pressure of volatile liquids, we use Raoult’s Law.
Who discovers Raoult's Law
?
- Raoult’s law has been named after François-Marie Raoult, a French chemist who while conducting an experiment found out that when substances were mixed in a solution, the vapour pressure of the solution decreased simultaneously.
- Raoult’s law was established in the year 1887 and is also considered the law of thermodynamics.
What is Raoult’s Law?
Raoult’s law states that:
 View Answer
View AnswerA solvent’s partial vapour pressure in a solution (or mixture) is equal or identical to the vapour pressure of the pure solvent multiplied by its mole fraction in the solution.
Mathematically, Raoult’s law equation is written as:
Psolution = Χsolvent P0solvent
Where,
Psolution = vapour pressure of the solution
Χsolvent = mole fraction of the solvent
P0solvent = vapour pressure of the pure solvent

Let's understand this by looking at the example below:
Let two volatile liquids A and B dissolve each other to form an ideal solution. Then the vapours above the solution will contain the vapours of A and B. Applying Dalton’s law of partial pressure the total vapour pressure of the solution will be
Psolution = PA + PB
Where,
PA and PB are the partial vapour pressures of A and B.
Solution being dilute (Condition for ideality) Raoult’s law can be applied.
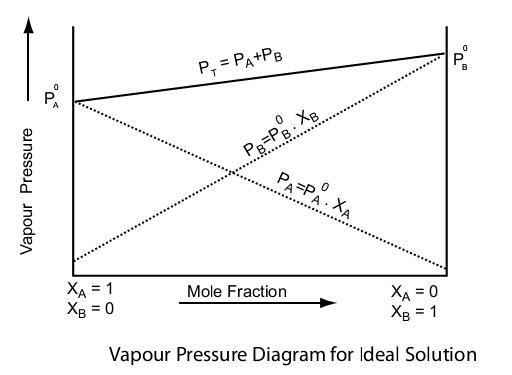
Raoult’s law for binary solutions state that
The vapour pressure of any volatile constituent of a binary solution at any given temperature is equal to the product of the vapour pressure of pure constituent and its mole fraction
PA = PºA XA
PB = PºB XB
Where:
- PºA and PºB are vapour pressures of pure A and B respectively
- xA and xB are mole fraction of A and B in liquid solution respectively
Hence, 𝑃 (Solution) 𝑜𝑟 Ps = PA0 XA + PB0 XB
Also, Ps = P0A(1-XB) + P0BXB
⇒ Ps = P0A+(P0B - P0A)XB
This equation is of the form y = mx + c. The value of m (slope) may be (+ve) or (–ve) depending upon whether P0B > P0A (m = + ve) or P0B < P0A (m = –ve).
Hence a plot of a graph of Ps versus XB will be a straight line with an intercept on the y-axis equal to pA and slope equal to (P0B - P0A)
Total Pressure of a Solution will be:
- P (Solution) = PA + PB = xAP0A + xBP0B

Vapour Composition
- Vapour composition means to find out the mole fraction of A and B in vapour i.e yA and yB.
- Dalton’s law of particle pressure is used to calculate the vapour composition, as we know, Partial pressure = mole fraction × total pressure
⇒ pA= yA × pS
or yA =𝑃A/𝑃𝑆
Similarly for B
⇒ yB = 𝑃A/𝑃𝑆
where yA and yB are mole fraction of ‘A’ and ‘B’ in the vapour phase and yA + yB = 1
SPECIAL NOTE:
xA and xB are mole fraction of ‘A’ and ‘B’ in the solution phase and xA + xB =1yA and yB are mole fraction of ‘A’ and ‘B’ in the vapour phase and yA + yB =1
Raoult's Law as a special case of Henry's law
- At given temperature liquids vaporize. At equilibrium, the pressure exerted by the vapour of the liquid over the liquid phase is referred to as vapour pressure.
- According to Raoult’s law, the vapour pressure of a volatile component in a given solution can be defined by pi = pi˚xi
- In an answer of a gas in a fluid one of the segments is volatile to the point that it exists as a gas and solvency is given by Henry's law which expresses that p = KH x
- Comparing both the equations we get that partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. Proportionality constant KH differs from pi˚
- Therefore, Raoult's law turns into a unique instance of Henry’s law in which KH get to be equivalent to pi˚
Limitations of Raoult’s Law
There are a few limitations to Raoult’s law:
- Raoult’s law is apt for describing ideal solutions. However, ideal solutions are hard to find and they are rare. Different chemical components have to be chemically identical equally.
- Since many of the liquids that are in the mixture do not have the same uniformity in terms of attractive forces, these type of solutions tends to deviate away from the law.
There is either a negative or a positive deviation. The negative deviation occurs when the vapour pressure is lower than expected from Raoult’s law. An example of negative deviation is a mixture of chloroform and acetone or a solution of water and hydrochloric acid.
Alternatively, positive deviation takes place when the cohesion between similar molecules is greater or that it exceeds adhesion between unlike or dissimilar molecules. Both components of the mixture can easily escape from the solution. An example of positive deviation includes the mixtures of benzene and methanol or ethanol and chloroform.
Example 1. The vapour pressure of ethanol and methanol are 44.5 mm and 88.7 mm Hg respectively. An ideal solution is formed at the same temperature by mixing 60 g of ethanol with 40g of methanol. Calculate the total vapour pressure of the solution.
Solution.
Number of moles of ethanol = 60/40 = 1.5
Number of moles of methanol = 40/32 = 1.25
XA = 1.25/1.25 + 1.3 = 0.4545 and XB = 1 – 0.4545 = 0.545
Let A = CH3OH, B = C2H5OH
Total pressure of the solution
PT = XAP0A + XBP0B
= 0.4545 × 88.7 + 0.545 × 44.5 = 40.31 + 24.27
= 64.58 mm Hg
Example 2. The composition of vapour over a binary ideal solution is determined by the composition of the liquid. If XA and YA are the mole fraction of A in the liquid and vapour, respectively find the value of XA for which YA − XA has a minimum. What is the value of the pressure at this composition?
Solution. 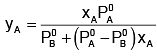
Subtracting xA from both sides, we get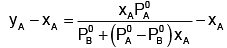
Now differentiating w.r.t. xA, we get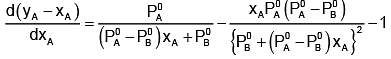
The value of xA at which yA − xA has a minimum value can be obtained by putting the above derivative equal to zero. Thus we have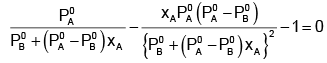
Solving for xA, we get
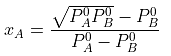
hence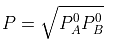
Example 3. A very small amount of non-volatile solute (that does not dissociate) is dissolved in 56.8 cm3 of benzene (density 0.889 g cm-3). At room temperature, the vapour pressure of this solution is 99.88 mm Hg while that of benzene is 100mm Hg. Find the molality of this solution. If the freezing temperature of this solution is 0.73 degrees lower than that of benzene. What is the value of the molal freezing point depression constant of benzene?
Solution.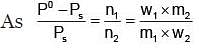
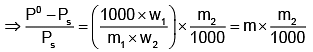
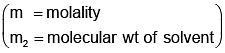
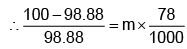
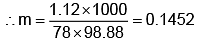
Also,
ΔTf = Kf × molality f
∴ 0.73 = K × 0.1452
fK = 5.028 K. molality
Example 4. What is the composition of the vapour which is in equilibrium at 30°C with a benzene-toluene solution with a mole fraction of benzene of 0.400?
(PoB = 119 torr and PTo = 37.0 torr)
Solution.
Total pressure of the solution is given by
PT = XB P0B + XTP0T
= 0.4 × 119 + 0.6 × 37
= 47.6 + 22.2
= 69.8 torr
Applying Dalton’s law for mole fraction in the vapour phase.
YB = PB/PT = 47.6/62.4
= 0.763
YT = 1– 0.763
= 0.237
Try Yourself!
Raoult’s Law states that the mole fraction of the solute component is directly proportional to its partial pressure.
On the basis of Raoult’s Law, liquid-liquid solutions are classified into two types of solutions, they are:
• Ideal Solutions
• Non-ideal Solutions
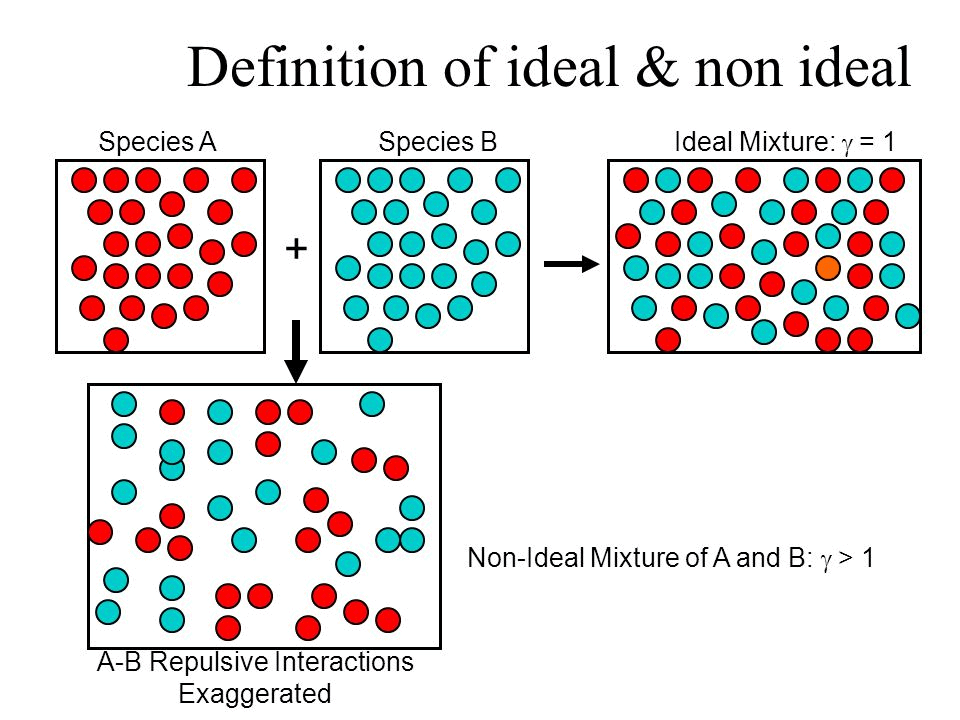
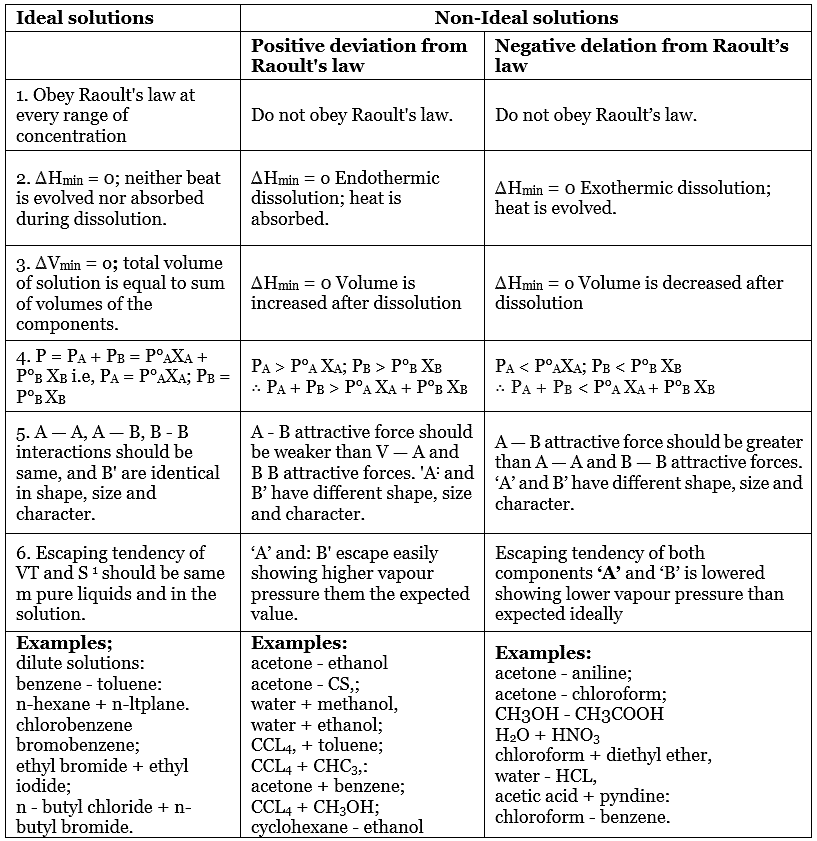
What is an Ideal Solution?
An ideal solution is a mixture in which the molecules of different species are distinguishable, however, unlike the ideal gas, the molecules in ideal solution exert forces on one another. When those forces are the same for all molecules independent of species then a solution is said to be ideal.
Characteristics of Ideal Solution
- The solutions which obey Raoult’s Law at every range of concentration and at all temperatures are called Ideal Solutions.
- We can obtain ideal solutions by mixing two ideal components that are, a solute and a solvent having similar molecular size and structure.
Example: consider two liquids A and B, and mix them. The formed solution will experience several intermolecular forces of attractions inside it, which will be:
• A – A intermolecular forces of attraction
• B – B intermolecular forces of attraction
• A – B intermolecular forces of attraction
- The solution is said to be an ideal solution, only when the intermolecular forces of attraction between A – A, B – B and A – B are nearly equal.

- They follow Raoult’s Law, which means partial pressure of components A and B in a solution will be PA = PA0 xA and PB = PB0 xB where PA0 and PB0 are respective vapour pressure in pure form and xA and xB are respective mole fractions of components A and B.
- The enthalpy of mixing of two components should be zero, that is, Δmix H = 0. This signifies that no heat is released or absorbed during mixing of two pure components to form ideal solution.
- The volume of mixing of two components should be zero that is, Δmix V = 0. This means that the total volume of solution is equal to the sum of the volume of solute and solution. Adding further, it also signifies that there is no occurrence of contraction or expansion of volume while mixing of two components.
- The solute-solute interaction and solvent-solvent interaction is nearly equal to solute-solvent interaction
Note: Perfectly ideal solutions are rare in nature, only some solutions show some ideal behaviour.
Examples of Ideal Solutions
- n-hexane and n-heptane
- Bromoethane and Chloroethane
- Benzene and Toluene
- CCl4 and SiCl4
- Chlorobenzene and Bromobenzene
- Ethyl Bromide and Ethyl Iodide
- n-Butyl Chloride and n-Butyl Bromide
What is a Non-Ideal Solution?
The solutions which don’t obey Raoult’s law at every range of concentration and at all temperatures are called Non-Ideal Solutions. Non-ideal solutions deviate from ideal solutions and are also known as Non-Ideal Solutions.
 Types of Non-Ideal Solutions
Types of Non-Ideal Solutions
Characteristics of Non-Ideal Solution
- The solute-solute and solvent-solvent interaction is different from that of solute-solvent interaction
- The enthalpy of mixing that is, Δmix H ≠ 0, which means that heat might have released if the enthalpy of mixing is negative (Δmix H < 0) or the heat might have observed if the enthalpy of mixing is positive (Δmix H > 0).
- The volume of mixing that is, Δmix V ≠ 0, which depicts that there will be some expansion or contraction in dissolution of liquids
Types of Non-Ideal Solution
- Non-ideal solutions showing positive deviation from Raoult’s Law
- Non-ideal solutions showing negative deviation from Raoult’s Law
Positive Deviation from Raoult’s Law
Example: consider two components A and B to form non-ideal solutions.
Let the vapour pressure, pure vapour pressure and mole fraction of component A be PA , PA0 and xA respectively and that of component B be PB , PB0 and xB respectively.
These liquids will show positive deviation when Raoult’s Law when
- PA > PA0 xA and PB > P0B xB, as the total vapour pressure (PA0 xA + P0B xB) is greater than what it should be according to Raoult’s Law.
- The solute-solvent forces of attraction is weaker than solute-solute and solvent-solvent interaction that is, A – B < A – A or B – B
- The enthalpy of mixing is positive that is, Δmix H > 0 because the heat absorbed to form new molecular interaction is less than the heat released on breaking of original molecular interaction
- The volume of mixing is positive that is, Δmix V > 0 as the volume expands on dissolution of components A and B
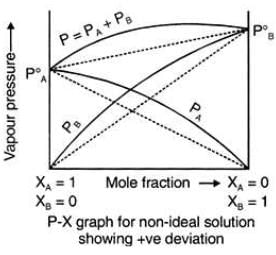
Examples: Following are examples of solutions showing positive deviation from Raoult’s Law
- Acetone and Carbon disulphide
- Acetone and Benzene
- Carbon Tetrachloride and Toluene or Chloroform
- Methyl Alcohol and Water
- Acetone and Ethanol
- Ethanol and Water
Negative Deviation from Raoult's Law
Negative Deviation occurs when the total vapour pressure is less than what it should be according to Raoult’s Law. Considering the same A and B components to form a non-ideal solution, it will show negative deviation from Raoult’s Law only when:- PA < PA0 xA and PB < P0B xB as the total vapour pressure (PA0 xA + P0B xB) is less than what it should be with respect to Raoult’s Law
- The solute-solvent interaction is stronger than solute-solute and solvent-solvent interaction that is, A – B > A – A or B – B
- The enthalpy of mixing is negative that is, Δmix H < 0 because more heat is released when new molecular interactions are formed
- The volume of mixing is negative that is, Δmix V < 0 as the volume decreases on dissolution of components A and B
Examples: Following are examples of solutions showing negative deviation from Raoult’s Law
- Chloroform and Benzene
- Chloroform and Diether
- Acetone and Aniline
- Nitric Acid ( HNO3) and water
- Acetic Acid and pyridine
- Hydrochloric Acid ( HCl) and water
 Image 5: Graph between vapour pressure and mole fraction
Image 5: Graph between vapour pressure and mole fraction
What are Azeotropes?
Azeotropes are defined as a mixture of two liquids which has a constant composition in the liquid and vapour phase at all temperatures.
- Azeotropes can’t be separated by fractional distillation, as the composition of the vapour phase remains the same after boiling.
- Because of uniform composition azeotropes are also known as Constant Boiling Mixtures.
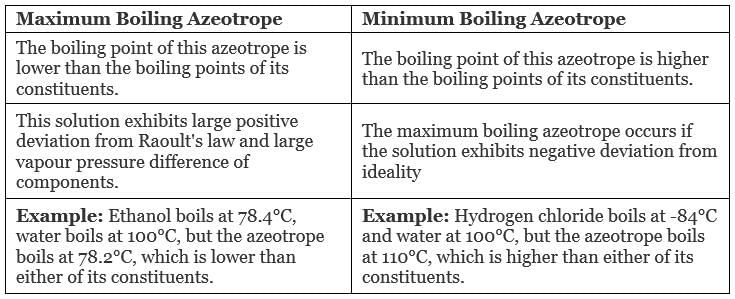
Each azeotrope has a characteristic boiling point.
The boiling point of an azeotrope is either less than the boiling point temperatures of any of its constituents (a positive azeotrope), or greater than the boiling point of any of its constituents (a negative azeotrope).
Types of Azeotropes
- Maximum Boiling Azeotrope
- Minimum Boiling Azeotrope
1. Maximum Boiling Azeotrope
Maximum Boiling Azeotrope is formed when we mix two non-ideal solutions at some specific composition, showing a large negative deviation from Raoult’s law.
Examples:
- Nitric Acid (HNO3) (68%) and water (32%) form maximum boiling azeotrope at a boiling temperature of 393.5 K
- Hydrochloric Acid (HCl) (20.24%) and water form maximum boiling azeotrope at a boiling temperature of 373 K
2. Minimum Boiling Azeotrope
Minimum Boiling Azeotrope is formed when we mix two non-ideal solutions at some specific composition, which shows a large positive deviation from Raoult’s Law.
Example: Ethanol ( 95.5%) and water (4.5%) form minimum boiling azeotrope at a boiling temperature of 351.5 K
|
117 videos|225 docs|239 tests
|
FAQs on Vapour Pressure, Raoult's Law, Ideal & Non Ideal Solutions - Physical Chemistry for NEET
| 1. What is vapor pressure? |  |
| 2. How is vapor pressure affected by temperature? |  |
| 3. How does the presence of solutes affect the vapor pressure of a liquid solution? |  |
| 4. How does the concentration of solutes affect the vapor pressure of a liquid solution? |  |
| 5. How is the vapor pressure of a liquid solution related to boiling point elevation? |  |


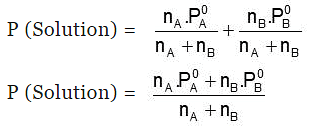
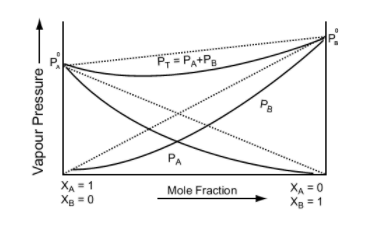 Image 5: Graph between vapour pressure and mole fraction
Image 5: Graph between vapour pressure and mole fraction



















