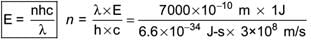Electromagnetic Radiation: Wave & Particle Nature | Chemistry Class 11 - NEET PDF Download
What is Electromagnetic Radiation?
Electromagnetic Radiation is a form of energy that travels through space in the form of waves. It consists of oscillating electric and magnetic fields that are perpendicular to each other and propagate at the speed of light. Here's a concise explanation:
 Electromagnetic Radiations
Electromagnetic Radiations
Definition:
- Electromagnetic radiation refers to energy propagated through space as electromagnetic waves.
- It consists of oscillating electric and magnetic fields perpendicular to each other.
- Electromagnetic waves travel at the speed of light.
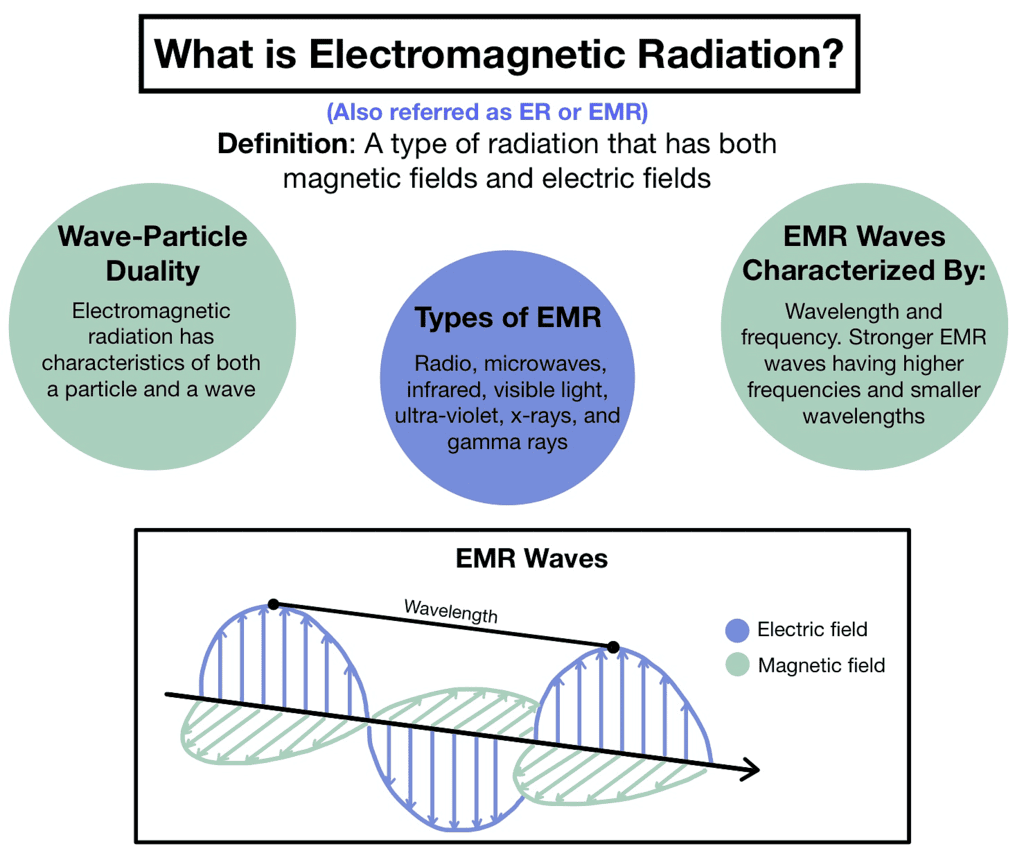
Spectrum:
- Electromagnetic radiation covers a broad spectrum of wavelengths.
- The spectrum includes radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.
- Each region of the spectrum has distinct properties and interacts with matter differently.
Regions of the Spectrum:
 Electromagnetic Spectrum
Electromagnetic Spectrum
- Radio waves: Longest wavelengths used for communication and broadcasting.
- Microwaves: Used in microwave ovens, telecommunications, and radar systems.
- Infrared radiation: Heat radiation is used in applications like remote controls and thermal imaging.
- Visible light: The narrow region of the spectrum visible to the human eye.
- Ultraviolet radiation: Higher energy than visible light, responsible for sunburns and used in sterilization and fluorescence.
- X-rays: High-energy radiation used for medical imaging and industrial applications.
- Gamma rays: Highest energy radiation emitted during nuclear reactions and radioactive decay.
Sources:
- Natural sources: The Sun, stars, and other celestial bodies.
- Artificial sources: Electronic devices like radios, TVs, cell phones, and medical equipment such as X-ray machines.
Importance:
- Essential in various scientific disciplines: physics, chemistry, biology, and astronomy.
- Practical applications in technology, communication, medicine, and research.
Properties and Parameters of Electromagnetic Radiations
Properties and parameters of electromagnetic radiation describe various characteristics and attributes associated with this form of energy. Here are some key properties and parameters:
1. Important Properties of EM Radiations
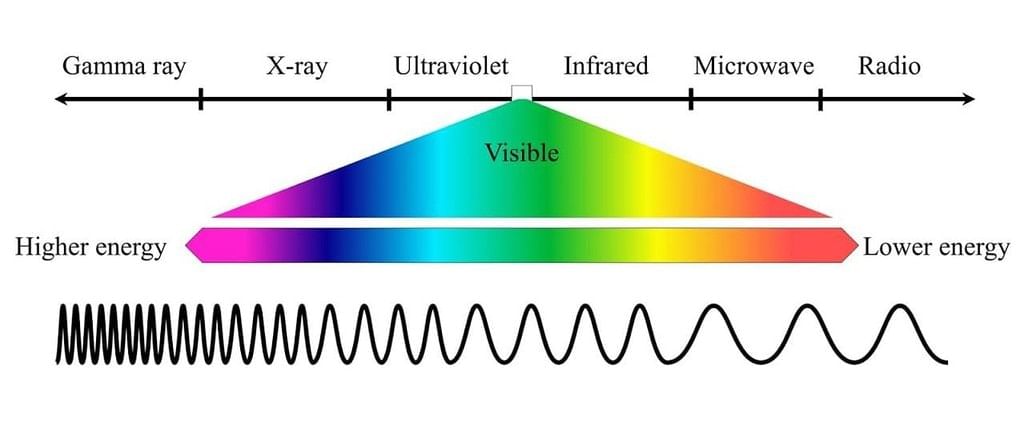
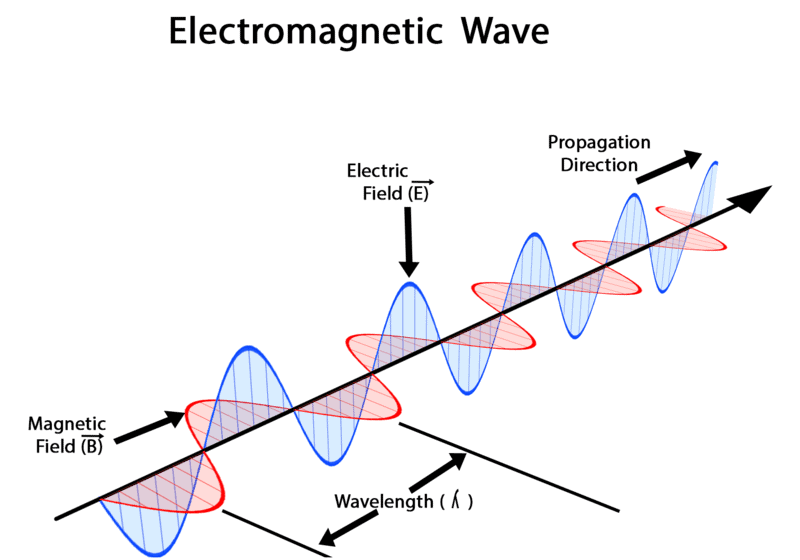
- Electric and Magnetic Fields Perpendicular to Each Other: The oscillating charged particles produce oscillating electric and magnetic fields which are perpendicular to each other and both are perpendicular to the direction of propagation of the wave.
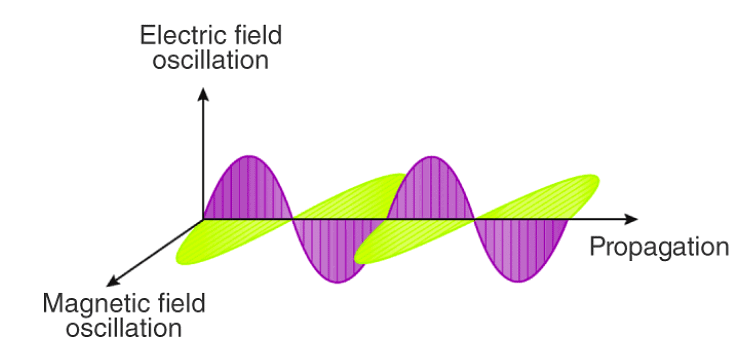 Electric and Magnetic Fields are Perpendicular
Electric and Magnetic Fields are Perpendicular
- No Medium Required: Unlike the sound and other waves in water, Electromagnetic waves do not require a medium i.e., they can travel in a vacuum too.
- Traveling at the same speed: In vacuum all types of electromagnetic radiation, regardless of wavelength, travel at the same speed, i.e., 3.0 × 108 m s–1 (2.997925 × 108 m s–1, to be precise). This is called the speed of light and is given the symbol ‘c‘. The frequency (ν ), wavelength (λ) and the velocity of the light is related to the equation:
c = ν λ where:
where:
c = speed of light
ν = frequency of the electromagnetic wave
λ = wavelength of the electromagnetic wave Different kinds of units are used to represent electromagnetic radiation.
Example: The speed of light in a vacuum is 3 × 108 meters per second (m/s). Calculate the frequency of light with a wavelength of 600 nanometers (nm) in a vacuum.
Solution:
- Speed of light (c) = 3 × 108 m/s
- Wavelength (λ) = 600 nm
To find: Frequency (ν) of light
We know that the speed of light is equal to the product of frequency and wavelength, i.e., c = νλ. Rearranging the equation, we get ν = c/λ.
Converting the wavelength from nanometers to meters:
600 nm = 600 × 10-9m
Substituting the values into the equation:
ν = (3 × 108 m/s) / (600 × 10-9m)
Simplifying the expression:
ν = 5 × 1014 Hz
Therefore, the frequency of light with a wavelength of 600 nm in a vacuum is 5 × 1014 hertz (Hz).
2. Important Parameters of EM Radiations
Electromagnetic Radiation is characterized based on various properties like frequency (ν ) , wavelength(λ) , time period etc. Apart from frequency and wavelength, some other parameters are also used to categorize electromagnetic radiation. One of these parameters is the wavenumber. ( ν̄).
 Wave Length, Amplitude & Frequency
Wave Length, Amplitude & Frequency
- Wavelength (λ): Wavelength is the distance between successive peaks or troughs of an electromagnetic wave. It is measured in meters (m) or other units such as nanometers (nm) or micrometers (μm). Different regions of the electromagnetic spectrum have different ranges of wavelengths.
- Frequency (ν): Frequency refers to the number of wave cycles that pass a given point per unit of time. It is measured in hertz (Hz) or other units such as kilohertz (kHz) or megahertz (MHz). Frequency and wavelength are inversely related by the equation: c = λν, where c is the speed of light.
- Amplitude: Amplitude represents the maximum displacement or strength of the electric and magnetic fields in an electromagnetic wave. It determines the intensity or brightness of the radiation. Higher amplitude corresponds to greater energy carried by the wave.
- Speed of light (c): The speed of light is a fundamental constant and represents the velocity at which electromagnetic waves propagate in a vacuum. It is approximately 299,792,458 meters per second (m/s) in a vacuum.
- Wave Number (ν̄): Wavenumber is a parameter that measures the number of wavelengths per unit length in electromagnetic radiation. Its units are reciprocal of the wavelength ν̄ unit, i.e., m–1. However, commonly used unit is cm–1
- Electromagnetic Spectrum: The electromagnetic spectrum encompasses the entire range of electromagnetic radiation. It includes different regions characterized by varying wavelengths and frequencies. Each region has unique properties and interactions with matter.
- Polarization: Polarization refers to the orientation of the electric field vector of an electromagnetic wave. It can be linear, circular, or elliptical, depending on the direction and magnitude of the field's oscillation.
 Polarization of Light
Polarization of Light
- Interaction with Matter: Electromagnetic radiation can interact with matter in various ways, depending on its frequency and properties. It can be absorbed, transmitted, or reflected by different materials, leading to a range of effects such as heating, chemical reactions, or excitation of electrons.
Understanding the properties and parameters of electromagnetic radiation is essential for fields such as optics, telecommunications, spectroscopy, and radiology. These characteristics enable us to manipulate and utilize electromagnetic radiation in numerous practical applications and scientific investigations.
Dual Behavior of Electromagnetic Radiation
Electromagnetic Radiation is light, which is present in a rainbow or a double rainbow. It also is a spectrum consisting of radio waves, microwaves, infrared waves, visible light, ultraviolet radiation, X-rays, and gamma rays. There are only two ways to transfer energy from one place to another place.
- Through a particle.
- Through a wave.
Electromagnetic radiation is a particle as well as a wave thus it is interesting to study its nature in quantum theory. Light is also electromagnetic radiation that contains frequencies.
 Dual Nature of Light
Dual Nature of Light
Wave Nature of Light
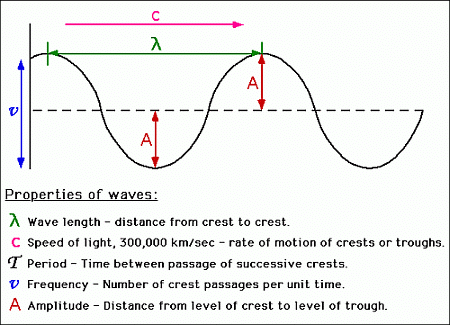
A wave is a physical phenomenon characterized by its frequency, wavelength, and amplitude. In general, waves transfer energy from one location to another, in which case they have a velocity.
Characteristics of Waves
- Amplitude: Maximum displacement from the mean position it remains constant with distance except for stationary or standing waves.
- Wavelength: It is the distance between two adjacent crest or troughs.
- Frequency (ν): The no of waves passing through a point in 1 second, unit-sec-1 or Hz.
- Wavenumber: No. of waves present in the unit distance.
etc.
- Velocity: linear distance traveled by wave in one second.
Maxwell Electromagnetic Wave Theory (Wave Nature of Light)
Here are the main points of Maxwell's electromagnetic wave theory :
1. Continuous Emission of Energy: Light is a constant release of energy from a source, known as radiant energy.
2. Oscillating Electric and Magnetic Fields: This energy consists of electric and magnetic fields that swing back and forth.
3. Perpendicular Orientation: These fields move at right angles to each other and perpendicular to the direction in which the radiation travels.
4. Electromagnetic Waves: The result is what we call electromagnetic waves or light waves.
5. Wave Characteristics: These waves exhibit characteristics of waves, like those seen in water ripples.
6. Speed of Light: They travel at an incredibly high speed, equivalent to the speed of light.
7. No Need for Material Medium: Unlike some other types of waves, these light waves can travel through empty space without needing any material substance.
In essence, Maxwell's theory helps us understand that light is a continuous flow of energy in the form of electromagnetic waves, characterized by oscillating electric and magnetic fields.
 Electromagnetic Wave
Electromagnetic Wave
Particle Nature of Light
- The emission of free electrons from a metal surface when the light is shone on it, is called the photoemission or the photoelectric effect. This effect led to the conclusion that light is made up of packets or quantums of energy.
- Now the question was whether the light quantum theory was indicative of the particle nature of light. Einstein already associated the light quantum with momentum. This strongly supported the particle nature of light and these particles were named photons.
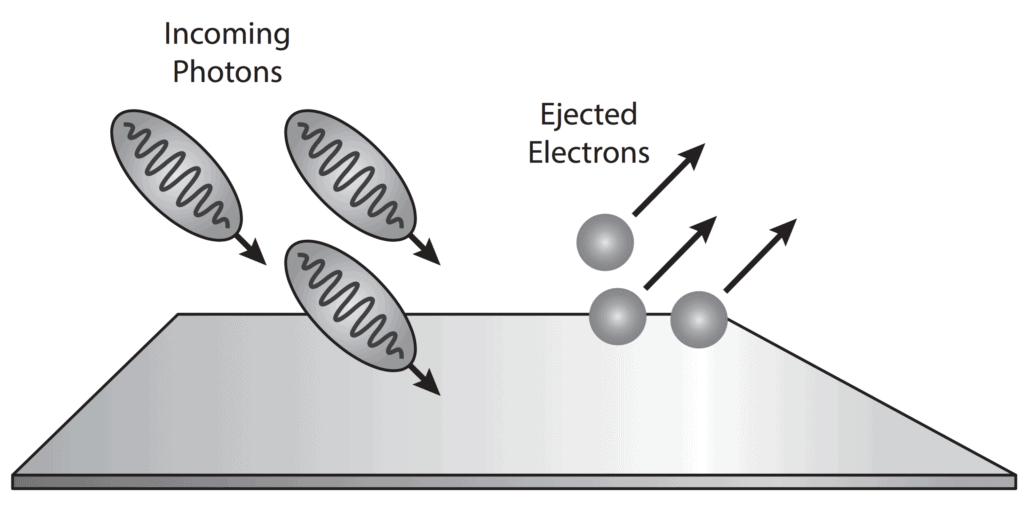 Particle Nature of Light
Particle Nature of Light
Planck's Quantum Theory
- He stated that a body radiates energy in the form of discontinuous energy packets or bundles. Each bundle of energy is known as quantum, and the quantum of light is known as photons. The energy of each quantum is directly proportional to the frequency of radiation.
E = hv
h = 6.62 × 10-34 Js.
Planck's Constant
- Total energy absorbed or emitted by a body will be whole no. integral multiple of the energy of quantum. i.e., Eabs or Eemitted = nhν.
Example 1: Calculate the no. of photons emitted by the 60-watt bulb in 10 hrs. When the light of wavelength 6000 Å is emitted by it.
= 6.5 × 1024 J
Example 2: Suppose we have a photon with a frequency of 5.0 × 1014 Hz. Calculate the energy of this photon using Planck's constant (h).
Using the equation E = hν, where ν represents the frequency, and h is Planck's constant (6.626 × 10-34 J·s), we can calculate the energy as follows:
E = (6.626 × 10-34 J·s) × (5.0 × 1014 Hz)
E ≈ 3.31 × 10-19 J
Therefore, the energy of the photon is approximately 3.31 × 10-19 Joules.
Energies in Electron Volts
- Room temperature thermal energy of a molecule = 0.04 eV
- Visible light photons = 1.5-3.5 eV
- Energy for the dissociation of a NaCl molecule into Na and Cl- ions: = 4.2 eV
- The ionization energy of atomic hydrogen = 13.6 eV
- Approximate energy of an electron striking a color television screen (CRT display) = 20,000 eV
- High energy diagnostic medical x-ray photons.= 200,000 eV (=0.2 MeV)
Typical Energies From Nuclear Decay:
- gamma = 0-3 MeV
- beta = 0-3 MeV
- alpha = 2-10 MeV
- Cosmic ray energies = 1 MeV - 1000 TeV
- 1 MeV = 106 eV, 1 GeV = 109 eV, 1 TeV = 1012 eV.
Explanation of Black Body Radiations Using Planck's Quantum Theory
- When a solid substance like the iron piece is heated, it emits radiation. As heating continues, more and more energy is being absorbed by the atom, and hence, more energy will be emitted, and therefore the energy of e.m.w. increases and frequency of e.m.w. increases and therefore, the body first becomes red then yellow, and finally white.
- Therefore, it can be concluded that light possesses a particle nature, and the energy of electromagnetic radiation depends upon frequency.
Explanation of Photoelectric Effect Using Planck's Quantum Theory
- When a metal sheet is subjected to electromagnetic radiation of suitable frequency then some electrons are ejected from the metal surface, and these electrons are known as photoelectrons, and the effect is known as the photoelectric effect.
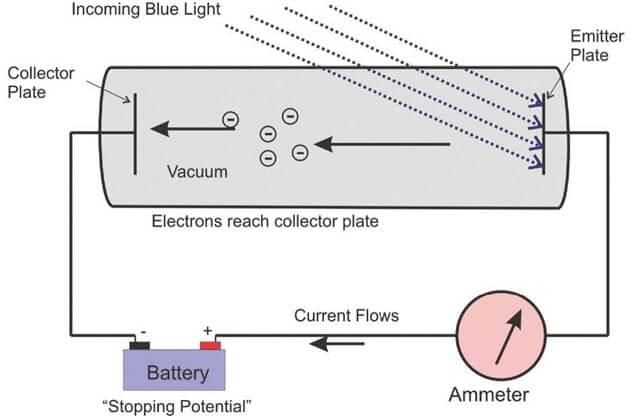 Photoelectric effect
Photoelectric effect
- If electromagnetic radiation of low frequency is used, then there is no ejection of electrons despite the continuously increasing intensity. This observation contradicted Maxwell's theory according to which energy electromagnetic radiation ∝ I but can be explained using Planck's quantum theory, i.e. E ∝ ν.
Photo-Electric Effect: Particle Nature of Light
Emission of an electron from the metal surface when the light of suitable frequency is subjected to the metal surface. The effect is known as the photoelectric effect and the ejected electrons are known as photoelectrons.
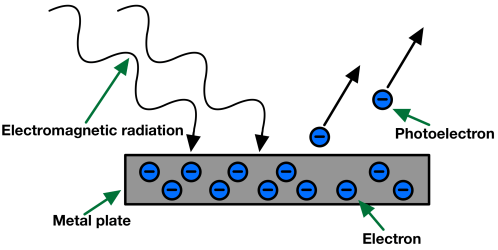 Photoelectric Effect
Photoelectric Effect
Terms Used in the Photoelectric Effect
1. Work function (w): It is the minimum amount of energy required to cause photoemission from the metal surface. It is also known as threshold energy or Binding energy. [Work function depends upon ionization energy and therefore w is minimum for alkali metals].
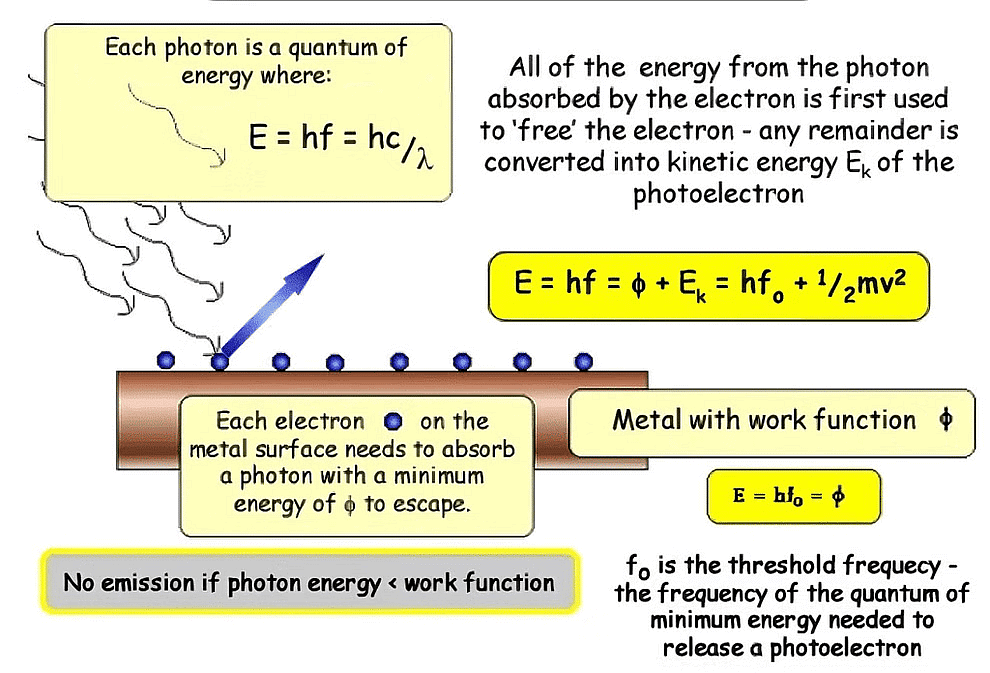 Work Function2. Threshold frequency (ν0): The minimum value of frequency that can cause photoemissions. If n < n0, then there is no photoemission.
Work Function2. Threshold frequency (ν0): The minimum value of frequency that can cause photoemissions. If n < n0, then there is no photoemission.
w = h ν0 ⇒
3. Threshold wavelength (l0): The maximum value of wavelength that can cause photoemission.
If l > l0, then photoemission is not possible.
4. Intensity (I): Energy falling on the metal surface of the unit area of unit time
5. Photo intensity (IP): It is the number of photons falling per unit area per unit time.
Relation between I and Ip: I = Ip hν
Photo intensity is independent of frequency while intensity depends on frequency.
6. Power: Total energy radiated per unit time.
Example 1: A photoelectric cell emits 3.6 × 1019 electrons when illuminated with light for 2 seconds. Calculate the power of the incident light.
Solution:
Given:
Number of emitted electrons (n) = 3.6 × 1019
Time (t) = 2 seconds
Charge of an electron (e) = 1.6 × 10-19 Coulombs (C)
First, calculate the total energy (E):
E = n × e
E = (3.6 × 1019) × (1.6 × 10-19)
E = 5.76 Joules
Now, use the formula P = E/t to find the power (P):
Power = E / t
Power = 5.76 Joules / 2 seconds
Power = 2.88 Watts
Therefore, the power of the incident light on the photoelectric cell is 2.88 Watts.
Example 2: The threshold frequency for a certain metal in the photoelectric effect is 2.5 × 1014 Hz. If a light source with a frequency of 3.2 × 1014 Hz is incident on the metal, will any electrons be emitted from the metal's surface?
To answer this question, we need to compare the frequency of the incident light with the threshold frequency of the metal.
- Threshold frequency (ν₀) = 2.5 × 1014 Hz
- Frequency of incident light (ν) = 3.2 × 1014 Hz
Solution:
If the frequency of the incident light (ν) is greater than or equal to the threshold frequency (ν₀), electrons will be emitted from the metal's surface. Otherwise, no electrons will be emitted.
Comparing the frequencies:
- ν = 3.2 × 1014 Hz
- ν₀ = 2.5 × 1014 Hz
Since ν > ν₀, the frequency of the incident light is greater than the threshold frequency. Therefore, electrons will be emitted from the metal's surface.
Effect of Variation of Frequency
- Effect of Photon Emission: I = Iphν
If the frequency of the subjected photon increases (intensity increases keeping photo intensity constant) then there is no change in the number of ejected photoelectrons as well as no change in photocurrent.
- Effect on kinetic Energy: Average k. E. as well as K.E.max increases with an increase in frequency.
hν - W = K Emax.
K Emax = hν - hν0 (y = mx + c)
K Emax = hν -
KEmax = hν - w
Example: The work function (w) of a certain metal is 4.2 eV, and a photon with a wavelength of 400 nm (1 nm = 10-9 m) is incident on the metal. Calculate the maximum kinetic energy (KEmax) of the emitted electrons.
To solve this, we'll need to use the equation for the maximum kinetic energy of emitted electrons:
KEmax = hν - w
Given:
Work function (w) = 4.2 eV
Wavelength (λ) = 400 nm = 400 × 10-9 m
Planck's constant (h) = 6.626 × 10-34 J·s (Joule-seconds)
First, let's calculate the frequency (ν) using the speed of light (c) formula:
c = λν
Rearranging the formula:
ν = c / λ
The speed of light is approximately 3.00 × 108 m/s.
ν = (3.00 × 108 m/s) / (400 × 10-9 m)
≈ 7.50 × 1014 Hz
Now, we can calculate the maximum kinetic energy (KEmax):
KEmax = hν - w
= (6.626 × 10-34 J·s) × (7.50 × 1014 Hz) - (4.2 eV)
To convert eV to Joules, we'll use the conversion factor: 1 eV = 1.602 × 10-19 J.
KEmax = (6.626 × 10-34 J·s) × (7.50 × 1014 Hz) - (4.2 eV × 1.602 × 10-19 J/eV)
Calculating:
KEmax ≈ 4.97 × 10-19 J - 6.726 × 10-19 J
≈ -1.756 × 10-19 J
Note: The calculated value for KEmax is negative, which implies that no electrons will be emitted since the energy of the incident photon is lower than the work function of the metal.
- Effect of Variation of Photo Intensity: On increasing intensity, keeping the frequency constant (i.e. increasing photo intensity) no. of ejected photoelectrons increases as well as photocurrent increases.
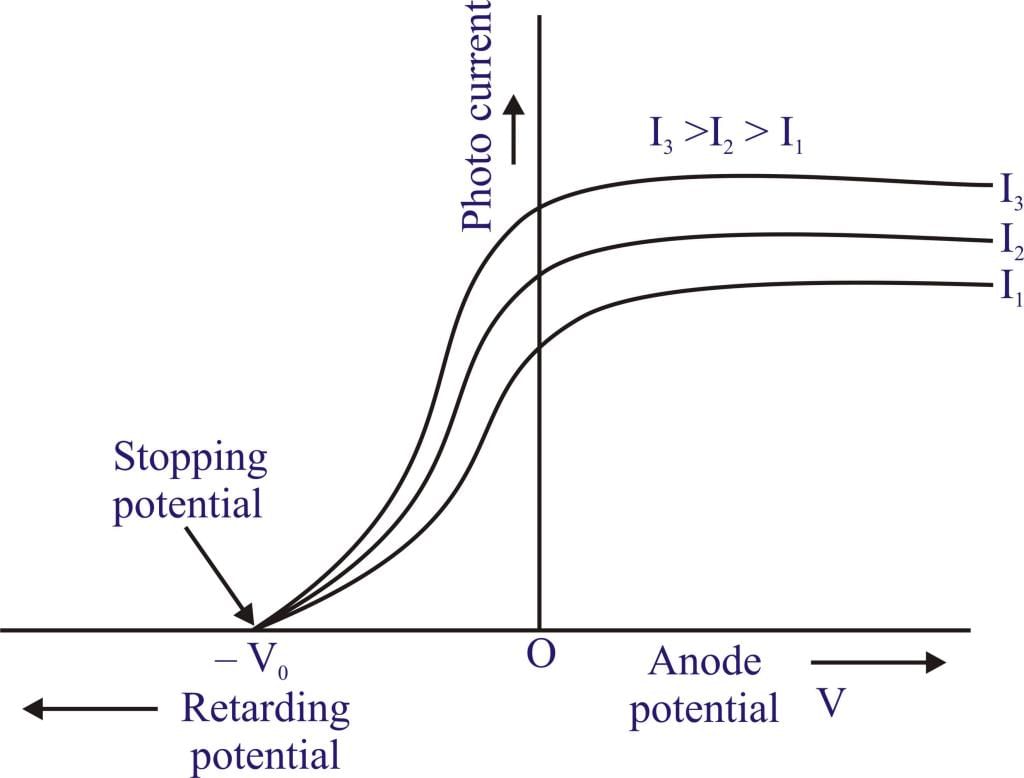 Graph of photocurrent vs voltage.
Graph of photocurrent vs voltage. - Effect on Kinetic Energy: Average K.E. and K.Emax remain constant with changes in photo intensity.
Stopping Potential or Retarding Potential (V0)
It is the minimum potential required to stop the fastest moving electrons completely or it is the minimum potential at which photocurrent becomes zero.
eV0 = hν - w
eV0 = hv - hn0
It can be commented that stopping potential increases with the increase in frequency however if photo intensity is changed there is no effect on stopping potential.
Graph of Photocurrent vs cell voltage.
Example 1: An ultraviolet light of wavelength 280 nm is used in an experiment of photoelectric effect with lithium cathode (Work Function = 2.5 eV). Then calculate
(i) K.Emax (ii) Stopping potential
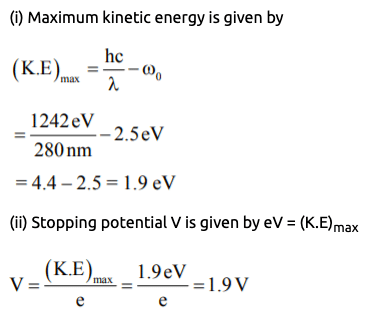
Some Important Questions
Q.1. Which properties among the following are false about electromagnetic waves?
(a) The energy in an electromagnetic wave is divided equally between electric and magnetic vectors.
(b) Both electric and magnetic field vectors are parallel to each other and perpendicular to the direction of propagation of the wave.
(c) These waves do not require any material medium for propagation
(d) Both electric and magnetic field vectors attain the maxima and minima at the same place and the same time
Answer: (b) The false statement is (b) "Both electric and magnetic field vectors are parallel to each other and perpendicular to the direction of propagation of the wave." In reality, these vectors are perpendicular to each other, and both are perpendicular to the direction of wave propagation.
Q.2. The ratio of the amplitude of the magnetic field to the amplitude of the electric field for electromagnetic wave propagation in a vacuum is equal to
(a) Unity
(b) Speed of light in vacuum
(c) Reciprocal of the speed of light in vacuum
(d) The ratio of magnetic permeability to electrical susceptibility in a vacuum.
Answer: (c) Reciprocal of the speed of light in vacuum
The ratio of the amplitude of the magnetic field (B0) to the amplitude of the electric field (E0) for an electromagnetic wave in a vacuum is given by the following relationship:
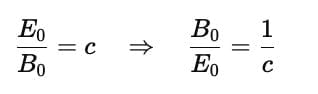
where c is the speed of light in a vacuum, approximately 3.00×108m/s. So, the correct answer is (c) Reciprocal of the speed of light in vacuum.
Q.3. The energy of the electromagnetic waves is of the order of 15 keV. To which part of the spectrum does it belong?
(a) X rays
(b) Infrared rays
(c) Ultraviolet rays
(d) Gamma rays
Answer: (a) X rays
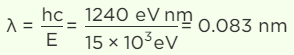
Since the order of wavelength is between 10 nm and 0.001 nm, it belongs to X-rays.
Q.4. In an electromagnetic wave in free space, the root mean square value of the electric field is Erms=6V/m. The peak value of the magnetic field is
(a) 1.41 x 10-8T
(b) 2.83 x 10-8T
(c) 0.70 x 10-8T
(d) 4.23 x 10-8T
Answer: (a) 2.83 x 10-8 T
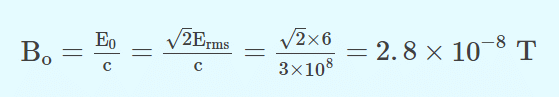
Q.5. Which of the following will emit photoelectrons when it collides with a metal?
a) UV radiation
b) Infrared radiation
c) Radio waves
d) Microwaves
Answer: Correct option will be (a) UV radiation
Reason: The photoelectric effect is the emission of electrons from a material when it is exposed to light. A sufficient frequency of light is required. It might be visible light, ultraviolet light, or X-rays. As a result, ultraviolet light causes electron emission.
|
119 videos|346 docs|74 tests
|
FAQs on Electromagnetic Radiation: Wave & Particle Nature - Chemistry Class 11 - NEET
| 1. What is electromagnetic radiation? |  |
| 2. What are the properties and parameters of electromagnetic radiations? |  |
| 3. What is the dual behavior of electromagnetic radiation? |  |
| 4. What is the wave nature of light? |  |
| 5. What is the particle nature of light as observed in the photoelectric effect? |  |