Maxwell's Equations & Displacement Current | Physics Class 12 - NEET PDF Download
Students are introduced to Maxwell's equations and the concept of displacement current. Maxwell's equations are usually covered as part of the study of electromagnetism in higher degrees. In this document, we will cover the introductory idea of Maxwell's equation and displacement current.
Maxwell's Equations
Maxwell's equations are a set of four fundamental equations that describe the behavior of electric and magnetic fields. These equations were formulated by James Clerk Maxwell in the 19th century and are crucial for understanding electromagnetism.
 James Maxwell
James Maxwell
Maxwell's equations are as follows:
1. Gauss's Law for Electricity:
Gauss's law for electricity states that the electric flux through a closed surface is proportional to the charge enclosed within that surface. Mathematically, it is expressed as:
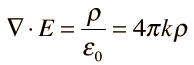
- E is the electric field.
- ρ is the charge density.
- ε0 is the permittivity of free space.
2. Gauss's Law for Magnetism:
Gauss's law for magnetism states that the magnetic flux through a closed surface is zero, indicating that magnetic monopoles do not exist. Mathematically, it is given by: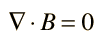
B is the magnetic field.
3. Faraday's Law of Electromagnetic Induction:
Faraday's law states that a changing magnetic field over time creates an electric field. This is the principle behind electromagnetic induction, which is the working mechanism of transformers, inductors, and many types of electrical generators and motors. The equation is:
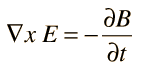
where symbols have the usual meaning
4. Ampère's Law with Maxwell's Addition:
Ampère's law relates the magnetic field around a closed loop to the electric current passing through the loop. Maxwell added a term to this law to account for the displacement current, making it consistent with the continuity equation. The modified equation is:
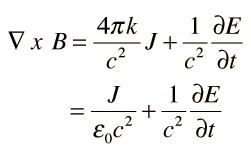
where J is the current density and
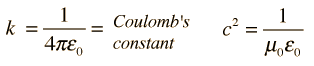
Displacement Current
- The concept of displacement current was introduced by Maxwell to address the inconsistencies in Ampère's law when applied to capacitors. Displacement current is not a current in the traditional sense, as it does not involve the movement of charge carriers. Instead, it represents a changing electric field in a region of space.
- Imagine you have a special kind of electricity called "displacement current." This concept is part of Maxwell's equations, which describe how electricity works. To understand displacement current, think about a capacitor, which is like a special electric storage device.
- When a capacitor starts charging, there is no conduction of charge between the plates. However, because of the change in charge accumulation with time above the plates, the electric field changes causing the displacement current as below:
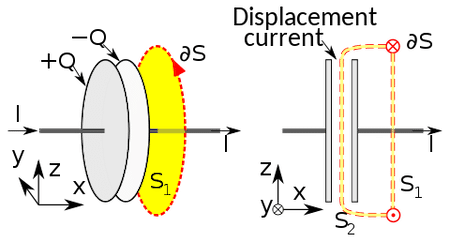 Displacement current in a capacitor
Displacement current in a capacitor
ID = JDS=S(∂D/∂t)
Where,
S is the area of the capacitor plate.
ID is the displacement current.
JD is the displacement current density.
D is related to electric field E as D = εE
ε is the permittivity of the medium in between the plates.
- Now, displacement current is basically how fast the electric stuff inside the capacitor is changing. We measure this change using something called the electric displacement field (D). So, displacement current is just a way to describe the quick changes happening in the electric field inside a capacitor.
Summary
Maxwell's equations provide a comprehensive framework for understanding the interplay between electric and magnetic fields and how they are influenced by charges and currents in space. The addition of the displacement current term ensures that these equations are consistent and describe electromagnetic phenomena accurately.
|
74 videos|314 docs|88 tests
|
FAQs on Maxwell's Equations & Displacement Current - Physics Class 12 - NEET
| 1. What are Maxwell's Equations? |  |
| 2. What is the significance of Maxwell's Equations in physics? |  |
| 3. What is the Displacement Current in Maxwell's Equations? |  |
| 4. How does the Displacement Current relate to electromagnetic waves? |  |
| 5. How do Maxwell's Equations and the Displacement Current impact technology today? |  |

















