Kinematic Equations: Uniformly Accelerated Motion | Physics Class 11 - NEET PDF Download
Kinematic Equations of Motion
If an object starts with velocity ”u” and after some time “t” its velocity changes to v, if the uniform acceleration is "a" and the distance traveled in time (t) is "s", then we obtain the following kinematic equations of uniformly accelerated motion.

What is Kinematics?
- Kinematics is a branch of physics that deals with the motion of objects without considering the forces that cause the motion.
- It focuses on describing how objects move, their positions, velocities, and accelerations over time.
- Kinematics provides the tools to analyze and predict the motion of objects in different situations, making it a crucial aspect of classical mechanics.
When to Use Kinematic Equations
- Kinematic equations are applicable in situations where an object is moving with a constant acceleration.
- They are commonly used in one-dimensional motion scenarios, such as a car moving along a straight road or an object falling vertically under gravity.
- With suitable modifications, these equations can also be applied to two-dimensional and three-dimensional motion, like a projectile launched at an angle or a rocket moving through the atmosphere.
Understanding the Equations of Motion
In the field of physics, the equations of motion are fundamental tools used to describe how a physical system evolves over time. These equations are particularly useful when dealing with situations involving uniform acceleration. There are three primary equations of motion, each serving a specific purpose in calculating various aspects of a moving object.
1. First Equation of Motion:
- Formula:. = u + at
- Variables Explained:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time taken
- Purpose: This equation relates the final velocity of an object to its initial velocity, acceleration, and the time taken for the motion.
2. Second Equation of Motion:
- Formula:. = ut + 1/2 at 2
- Variables Explained:
- s = displacement
- u = initial velocity
- a = acceleration
- t = time taken
- Purpose: This equation calculates the displacement of an object based on its initial velocity, acceleration, and the time taken.
3. Third Equation of Motion:
- Formula: v 2 = u 2 + 2as
- Variables Explained:
- v = final velocity
- u = initial velocity
- a = acceleration
- s = displacement
- Purpose: This equation establishes a relationship between the velocities, acceleration, and displacement of an object.
These equations are applicable in scenarios involving uniform acceleration, where the acceleration remains constant throughout the motion. They are essential for solving various problems in kinematics, the branch of physics that deals with the motion of objects.
Derivation of Equation of Motion
The equations of motion can be derived using the following methods:
- By Simple Algebraic Method
- By Graphical Method
- By Calculus Method
In the next few sections, the equations of motion are derived by all the three methods in a simple and easy to understand way.
Derivation of First Equation of Motion
For the derivation, let us consider a body moving in a straight line with uniform acceleration. Then, let the initial velocity be u, acceleration is denoted as a, time period is denoted as t, velocity is denoted as v, and the distance travelled is denoted as s.
Derivation of First Equation of Motion by Algebraic Method
We know that the acceleration of the body is defined as the rate of change of velocity.
Mathematically, acceleration is represented as follows:
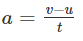
where v is the final velocity and u is the initial velocity.
Rearranging the above equation, we arrive at the first equation of motion as follows:
v = u + at
Derivation of First Equation of Motion by Graphical Method
The first equation of motion can be derived using a velocity-time graph for a moving object with an initial velocity of u, final velocity v, and acceleration a.
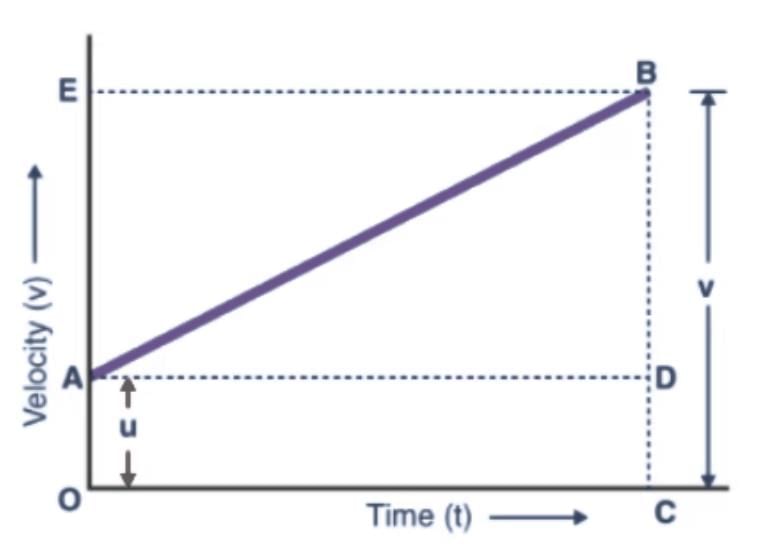
In the above graph,
- The velocity of the body changes from A to B in time t at a uniform rate.
- BC is the final velocity and OC is the total time t.
- A perpendicular is drawn from B to OC, a parallel line is drawn from A to D, and another perpendicular is drawn from B to OE (represented by dotted lines).
Following details are obtained from the graph above:
The initial velocity of the body, u = OA
The final velocity of the body, v = BC
From the graph, we know that
BC = BD + DC
Therefore, v = BD + DC
v = BD + OA (since DC = OA)
Finally,
v = BD + u (since OA = u) (Equation 1)
Now, since the slope of a velocity-time graph is equal to acceleration a,
So,
a = slope of line AB
a = BD/AD
Since AD = AC = t, the above equation becomes:
BD = at (Equation 2)
Now, combining Equation 1 & 2, the following is obtained:
v = u + at
Derivation of First Equation of Motion by Calculus Method
Since acceleration is the rate of change of velocity, it can be mathematically written as:
a = dv/dt
Rearranging the above equation, we get
adt = dv
Integrating both the sides, we get
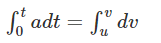
at = v − u
Rearranging, we get
v = u + at
Derivation of Second Equation of Motion
For the derivation of the second equation of motion, consider the same variables that were used for derivation of the first equation of motion.
Derivation of Second Equation of Motion by Algebraic Method
Velocity is defined as the rate of change of displacement. This is mathematically represented as:
Velocity = Displacement/Time
Rearranging, we get
Displacement = Velocity × Time
If the velocity is not constant then in the above equation we can use average velocity in the place of velocity and rewrite the equation as follows:
Displacement = 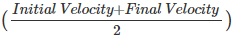 × Time
× Time
Substituting the above equations with the notations used in the derivation of the first equation of motion, we get
s = u+v/2 × t
From the first equation of motion, we know that v = u + at. Putting this value of v in the above equation, we get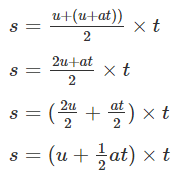
On further simplification, the equation becomes:
s = ut + 1/2 at2
Derivation of Second Equation of Motion by Graphical Method
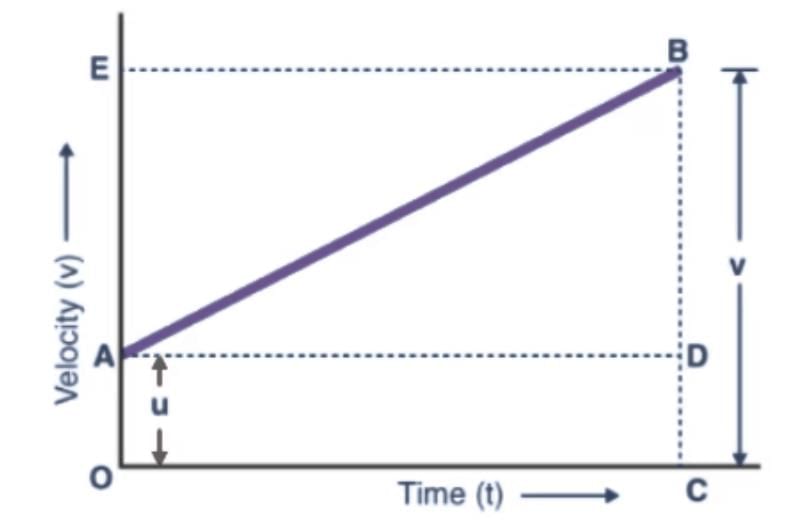
From the graph above, we can say that
Distance travelled (s) = Area of figure OABC = Area of rectangle OADC + Area of triangle ABD
s = (1/2AB × BD)+(OA × OC)
Since BD = EA, the above equation becomes
s = (1/2AB × EA) + (u × t)
As EA = at, the equation becomes
s = 1/2 × at × t + ut
On further simplification, the equation becomes
s = ut + 1/2at2
Derivation of Second Equation of Motion by Calculus Method
Velocity is the rate of change of displacement.
Mathematically, this is expressed as
v = ds/dt
Rearranging the equation, we get
ds = vdt
Substituting the first equation of motion in the above equation, we get
ds = (u + at)dt
ds = (u + at)dt = (udt + atdt)
On further simplification, the equation becomes:
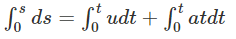
= ut + 1/2at2
Derivation of Third Equation of Motion
Derivation of Third Equation of Motion by Algebraic Method
We know that, displacement is the rate of change of position of an object. Mathematically, this can be represented as:
Displacement = 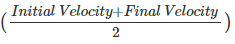 × t
× t
Substituting the standard notations, the above equation becomes
s = 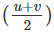 × t
× t
From the first equation of motion, we know that
v = u + at
Rearranging the above formula, we get
t = v − u/a
Substituting the value of t in the displacement formula, we get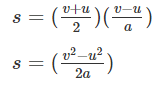
2as = v2 − u2
Rearranging, we get
v2 = u2 + 2as
Derivation of Third Equation of Motion by Graphical Method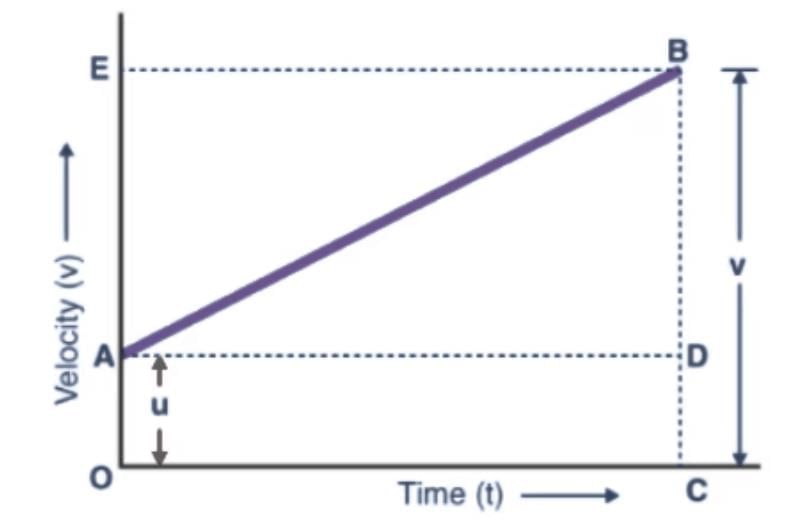 From the graph, we can say that
From the graph, we can say that
The total distance travelled, s is given by the Area of trapezium OABC.
Hence,
S = ½ (Sum of Parallel Sides) × Height
S = (OA+CB) × OC
Since, OA = u, CB = v, and OC = t
The above equation becomes
S= ½ (u+v) × t
Now, since t = (v – u)/ a
The above equation can be written as:
S= ½ ((u+v) × (v-u))/a
Rearranging the equation, we get
S= ½ (v+u) × (v-u)/a
S = (v2 - u2)/2a
Third equation of motion is obtained by solving the above equation:
v2 = u2 + 2aS
Derivation of Third Equation of Motion by Calculus Method
We know that acceleration is the rate of change of velocity and can be represented as:
a = dv/dt (1)
We also know that velocity is the rate of change of displacement and can be represented as:
v = ds/dt (2)
Cross multiplying (1) and (2), we get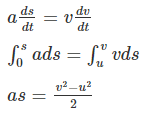
⇒ v2 = u2 + 2as
Solved Examples:
Q1. An automobile travelling with a speed of 60 Km/h can apply brake to stop within a distance of 20 m If the car is going twice as fast i.e., 120 Km/h the stopping distance will be
A. 60m
B. 40m
C. 20m
D. 80m
Answer: D
We know that the stopping distance is proportional to the square of the speed.
So,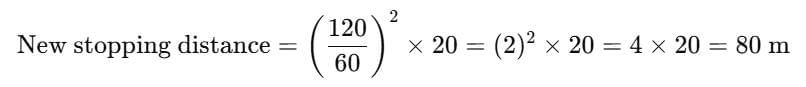
Therefore, the stopping distance at 120 km/h will be 80 metres.
Q2. A cart that is free to move in one dimension is moving in the positive direction and slowing down under the influence of a constant backward pull until the cart comes to a momentary stop and reverses direction. What are the signs of the cart’s velocity and acceleration during the moment it is stopped?
A. velocity : 0 acceleration : +
B. acceleration : 0 velocity : +
C. velocity : 0 acceleration : –
Answer: At the moment the cart is stopped, its velocity is zero because it is at rest at that instant.
However, the acceleration remains constant and is directed in the negative direction (backward pull), which caused the cart to slow down and eventually reverse direction.
So,
- Velocity = 0 (since the cart is momentarily at rest)
- Acceleration = Negative (since the pull is in the backward direction)
Motion Under Gravity (Free Fall)
Acceleration produced in a body by the force of gravity, is called acceleration due to gravity. It is represented by the symbol g.
Value of g = 9.8 m/s2 = 980 cm/s2 = 32 ft/s2
In the absence of air, it is found that all bodies (irrespective of the size, weight or composition) fall with the same acceleration near the surface of the earth. This motion of a body falling towards the earth from a small altitude (h << earth's radius) is called motion under gravity. Free fall means acceleration of body is equal to acceleration due to gravity.
If a Body is Projected Vertically Upward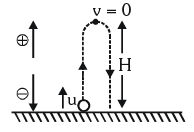 Positive / Negative directions are a matter of choice. You may take another choice.
Positive / Negative directions are a matter of choice. You may take another choice.
(i) Equations of motion: Taking initial position as origin and direction of motion (i.e. vertically up) as positive a = – g [As acceleration is downwards while motion upwards]
So, if a body is projected with velocity u and after time t it reaches a height h then
v = u - gt, h = ut - 1/2gt2
v2 = u2 - 2gh, hnth = u - g/2(2n - 1)
(ii) For maximum height v = 0
So from above equation u = g t
it is called time of ascent (t1) = u/g
In case of motion under gravity, time taken to go up is equal to the time taken to fall down through the same distance. Time of descent (t2) = time of ascent (t1) = u/g
∴ Total time of flight T = t1 + t2 = 2u/g
and u2 = 2gh ⇒ H = u2/2g
If a Body is Projected Vertically Downward With Some Initial Velocity From Some Height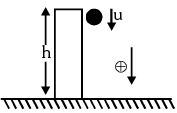
Equations of motion: Taking initial position as origin and direction of motion (i.e., downward direction) as a positive, we have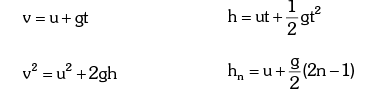
|
119 videos|491 docs|98 tests
|
FAQs on Kinematic Equations: Uniformly Accelerated Motion - Physics Class 11 - NEET
| 1. What are the kinematic equations of motion? |  |
| 2. How are the kinematic equations of motion derived? |  |
| 3. What are the kinematic equations for uniformly accelerated motion? |  |
| 4. How can the kinematic equations of motion be used in problem-solving? |  |
| 5. Can the kinematic equations of motion be used for non-uniformly accelerated motion? |  |






















