Introduction to Motion in a Plane | Science & Technology for UPSC CSE PDF Download
Introduction
Welcome to the fascinating world of motion in a plane!
- To describe motion beyond one dimension, we need something more powerful than simple signs ( scalars).
- Vectors come into play here—arrows that represent both the magnitude and the direction of physical quantities like velocity and acceleration.
- But before we dive deeper, we need to answer a few important questions:
(i) What is a vector?
(ii) How do we add, subtract, or multiply vectors?
(iii) What happens when we multiply a vector by a real number? - Once we master the language of vectors, we'll be able to describe motion in a plane.
- We'll explore some interesting scenarios:
(i) Motion with constant acceleration (e.g., projectile motion)
(ii) Uniform circular motion (e.g., the rotation of a Ferris wheel)
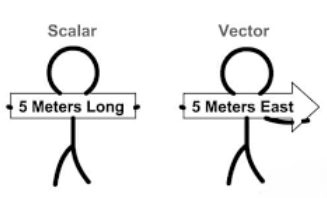
Scalar and Vectors
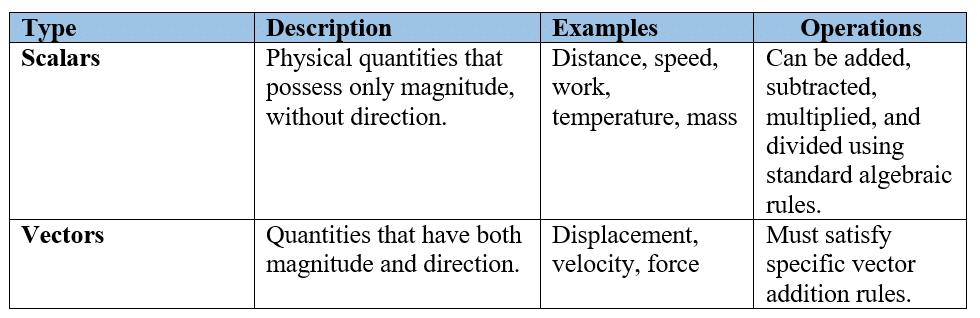
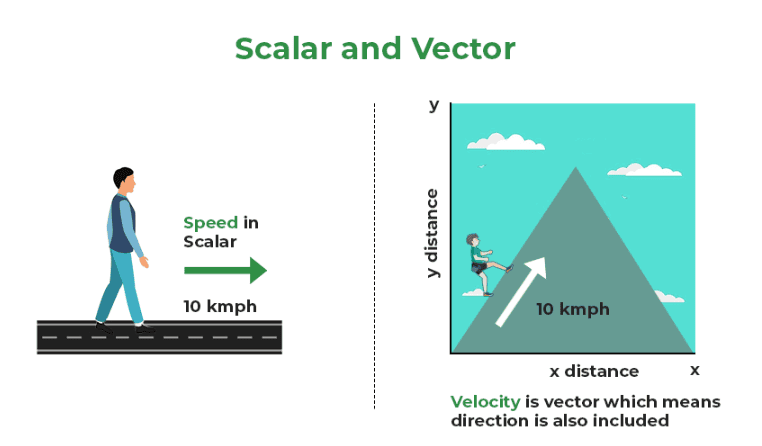

Types of Vectors
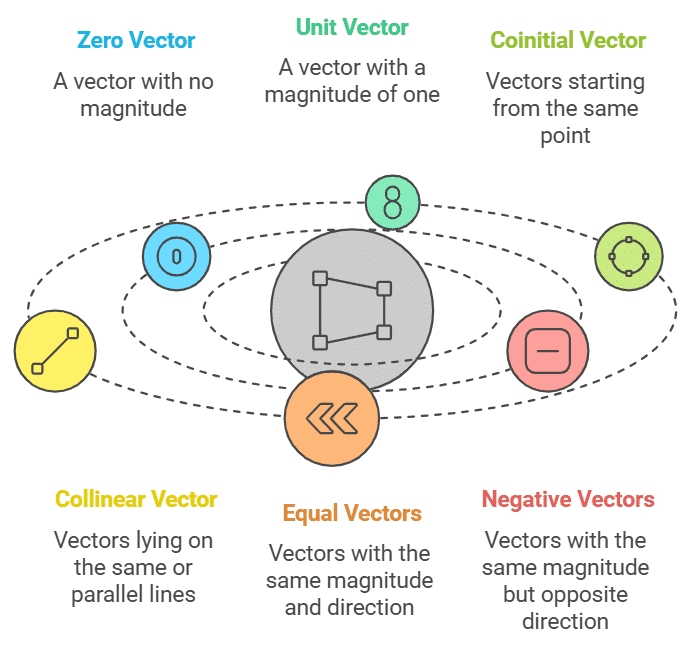 Vector Types
Vector Types
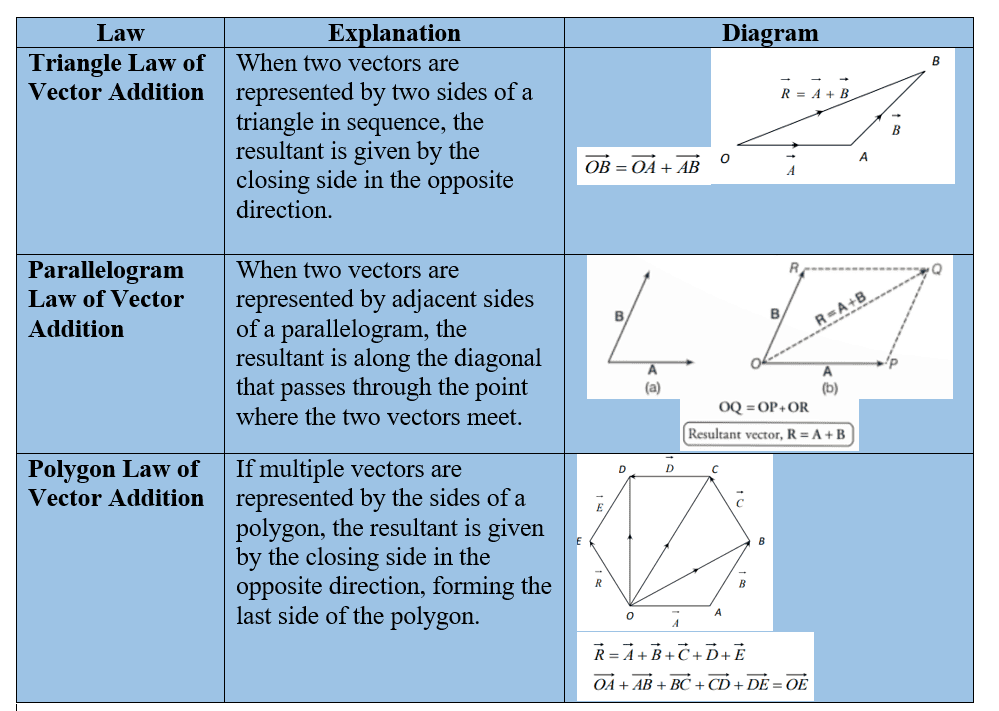
Addition of vectors
The addition of vectors can be performed using three main laws:
1. Triangle Law of Vector Addition
2. Parallelogram Law of Vector Addition
3. Polygon Law of Vector Addition
Resolution of Vectors
Any vector can be resolved into two components along two mutually perpendicular directions.
Suppose a vector A makes an angle θ with the x-axis:
Ax= A cosθ, Ay = A sinθThe vector is expressed as
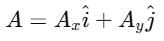
Vector Addition – Analytical Method
If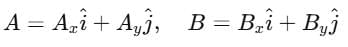
Then,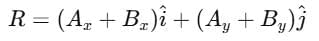
Magnitude: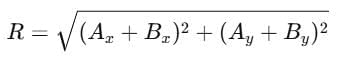
Direction: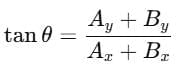
For two vectors A and B with angle θ:
Law of Cosines:
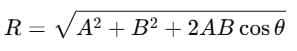
Law of Sines:
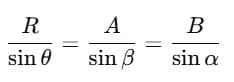
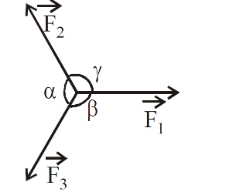
Lami's Theorem
It states that if three forces acting at a point are in equilibrium, then the magnitude of each force is proportional to the sine of the angle between the other two forces.
Mathematically, this can be expressed as:
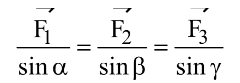
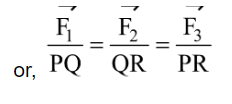
This means that the ratio of each force to the sine of the angle between the other two forces remains constant.
Relative Velocity
In two-dimensional motion, when two objects A and B are moving with velocities VB relative to a common reference frame, we can define their relative velocities as follows:
- Relative velocity of A with respect to B:
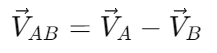
This indicates that object A is moving relative to object B.
- Relative velocity of B with respect to A:
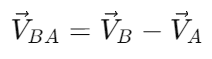
It can be observed that the magnitude of these relative velocities is the same, meaning:
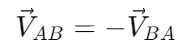
and 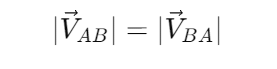
Thus, the relative velocities between two objects have equal magnitudes but opposite directions.
Motion in a Plane
Position Vector and Displacement
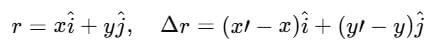
Velocity
Average velocity:
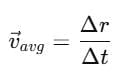
Instantaneous velocity:
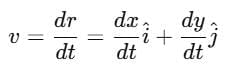
Acceleration
Average acceleration
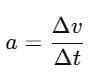
Instantaneous acceleration:
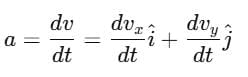
Motion in a Plane with Constant Acceleration
For constant acceleration:
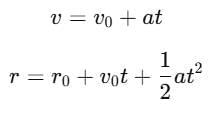
In components:
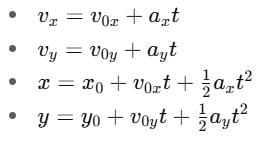
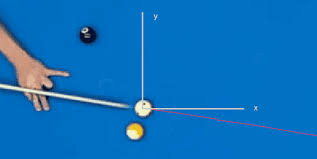
Motion in a Plane or Motion in Two Dimension
Motion in which a body's movement is confined to a plane is referred to as plane motion.
- An object's motion is classified as two-dimensional if two of the three coordinates needed to define its position in space change over time.
- In this type of motion, the object moves within a plane.
- Examples include a billiard ball rolling on a table, an insect crawling across a floor, and the Earth orbiting the sun.
- Two specific types of two-dimensional motion are:
1. Projectile motion
2. Circular motion
1. Projectile Motion
A projectile refers to a body that is launched with an initial velocity in any direction and subsequently moves solely under the influence of gravity.
Examples: A football kicked by a player, a stone thrown from a building, and a bomb dropped from an airplane.
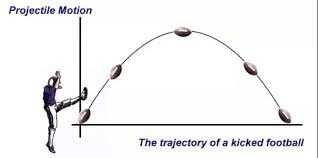
- The path taken by the projectile is known as its trajectory.
- The projectile experiences two types of motion:
(i) a constant horizontal velocity that remains unchanged (assuming no air resistance) and
(ii) a vertical velocity that changes uniformly due to gravity. - The horizontal and vertical motions occur independently of one another.
- Assumptions of Projectile Motion
(i) There is no resistance due to air.
(ii) The effect of the curvature of earth is negligible.
(iii) The effect due to rotation of earth is negligible.
(iv) For all points of the trajectory, the acceleration due to gravity ‘g’ is constant in magnitude and direction.
2. Circular Motion
- Circular motion is a type of motion that occurs in two dimensions.
- For an object to move in a circular path, it must be given an tangential velocity, and a force must act on it.
- This force is always directed at right angles to the object’s velocity at any given instant.
- Since the force acts perpendicular to the displacement of the object, no work is done by the force, meaning the kinetic energy and speed of the object remain unchanged.
- However, the combined effect of centripetal force and the object's velocity causes it to follow a circular path.
- When an object moves with constant speed in a circular path of radius R:
Velocity: v = ωR
Centripetal acceleration: ac = v²/R = ω²R (directed towards centre)
Time period: T = 2π/ω
Frequency: ν = 1/T
Relations:
v = 2πRν
ac = 4π²ν²R
- Circular motion can be divided into two categories:
(i) Uniform circular motion (where the speed remains constant)
(ii) Non-uniform circular motion (where the speed changes over time)

Solved Examples for You
Q1. The state with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
- adding any two scalars,
- adding a scalar to a vector of the same dimensions,
- multiplying any vector by any scalar,
- multiplying any two scalars,
- adding any two vectors,
- adding a component of a vector to the same vector.
Ans: 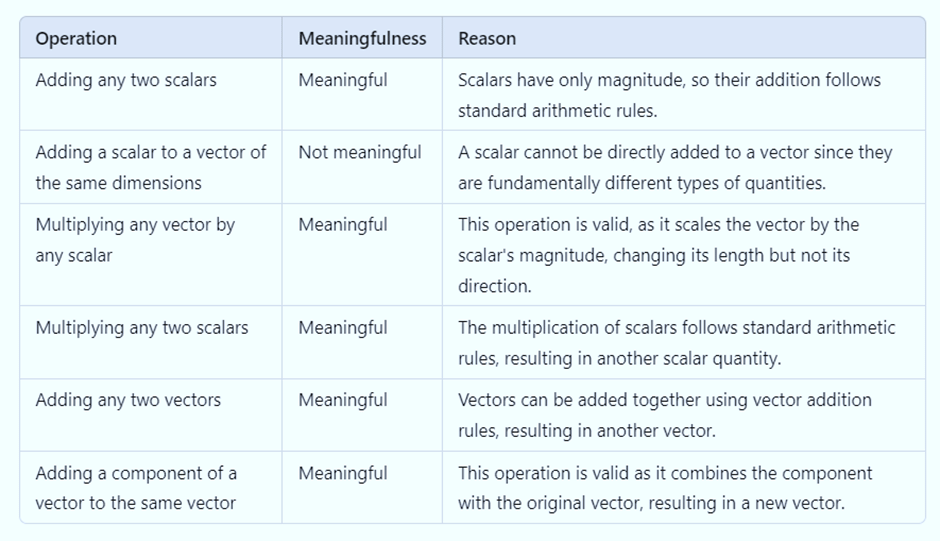
Q2. Read each statement below carefully and state with reasons, if it is true or false:
(a) The magnitude of a vector is always a scalar,
(b) each component of a vector is always a scalar,
Ans:
(a) True. The magnitude of a vector is a number. Hence, it is a scalar.
(b) False. Each component of a vector is also a vector.
Q3. What is a projectile? Prove that the path of a projectile is parabolic.
Ans: A projectile is any object thrown into space that is influenced only by the force of gravity is called a projectile.
We know that the equation of projectile is,
y = x tan θ – (gx2)/(2u2cos2θ )
Comparing the equation with the standard form y = ax + bx2, we find that
a = tanθ
b = – g/2u2cos2θ
The above equation of trajectory is similar to the equation of a parabola.
Hence, the path of a projectile is parabolic.
|
90 videos|488 docs|209 tests
|
FAQs on Introduction to Motion in a Plane - Science & Technology for UPSC CSE
| 1. What is the difference between scalar and vector quantities in physics? |  |
| 2. How do you calculate relative velocity between two objects? |  |
| 3. What are the key components of motion in a plane? |  |
| 4. How do you resolve vectors into their components? |  |
| 5. What is projectile motion and what are its key characteristics? |  |

















