Collisions | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Introduction |

|
| Types of Collisions |

|
| One-Dimensional or Head-on Collisions |

|
| Two-Dimensional or Oblique Collision |

|
Introduction
Collisions are fascinating events where a strong force acts between two or more bodies for a very short time, leading to changes in their energy and momentum.
Whether it's a collision between billiard balls or an interaction on a subatomic level, collisions showcase the key principles of physics.
1. Stages of Collision:
Collisions can be broken into three stages—before, during, and after the interaction.
- Before and after the collision, forces are absent.
- During the collision, large forces dominate and govern the motion.
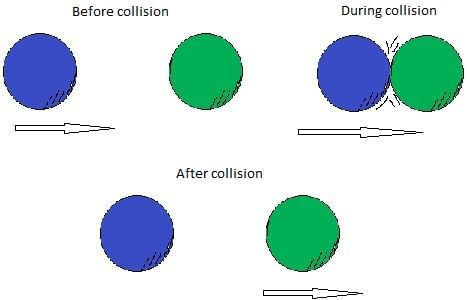
2. Conservation of Momentum and Energy:
- In an ideal system, the total momentum and energy remain conserved throughout the collision.
- This principle helps us relate initial and final velocities of the colliding objects, providing a deep insight into how motion evolves.
Types of Collisions
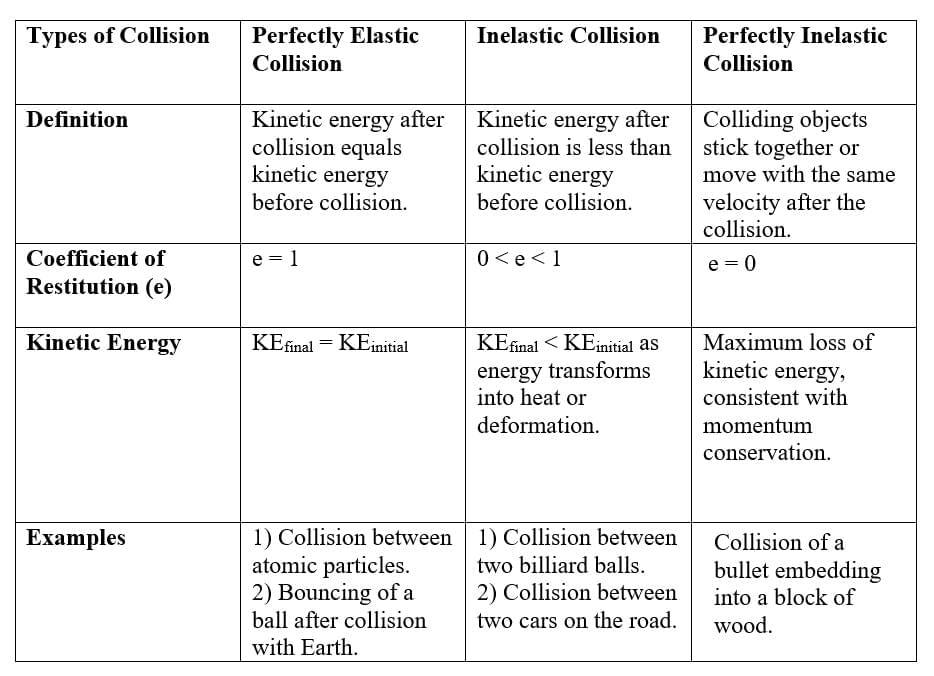
(i) On the basis of conservation of kinetic energy.
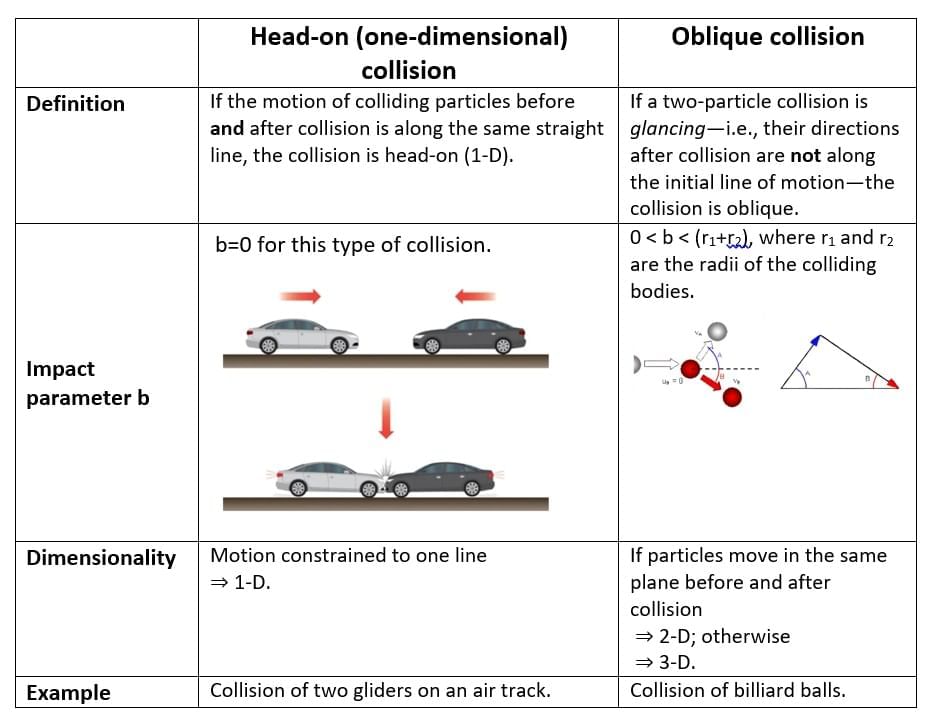
(ii) On the basis of the direction of colliding bodies:
1. Elastic collision
The collision in which both the momentum and the kinetic energy of the system remains conserved are called elastic collisions.
- In an elastic collision all the involved forces are conservative forces.
- Total energy remains conserved.
2. Inelastic collision
The collision in which only the momentum remains conserved but kinetic energy does not remain conserved are called inelastic collisions.
- In an inelastic collision some or all the involved forces are non-conservative forces.
- Total energy of the system remains conserved.
- If after the collision two bodies stick to each other, then the collision is said to be perfectly inelastic.
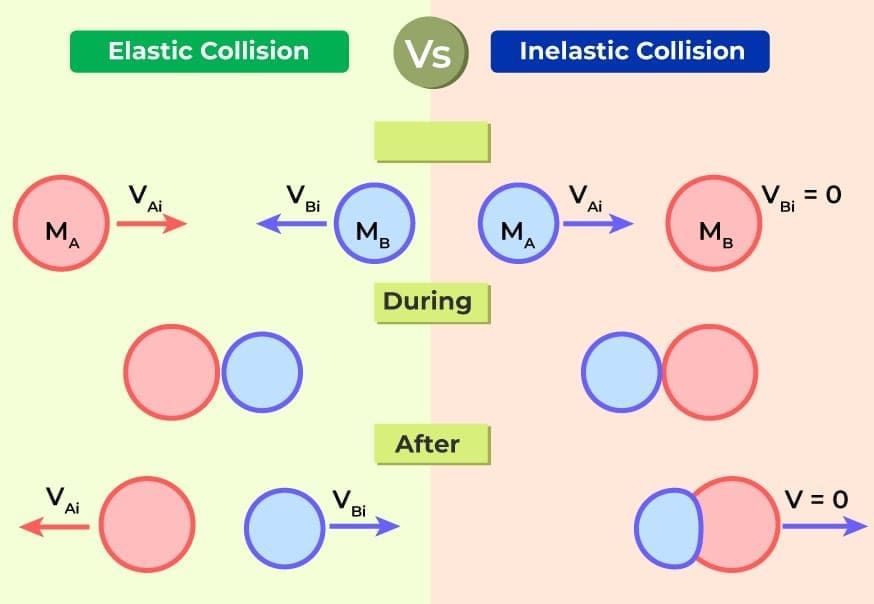
One-Dimensional or Head-on Collisions
If the initial and final velocities of colliding bodies lie along the same line, then the collision is called one dimensional or head-on collision.
Inelastic One Dimensional Collision
Applying Newton’s experimental law, we have
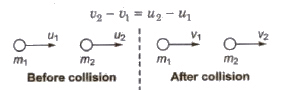
- Velocities after collision:
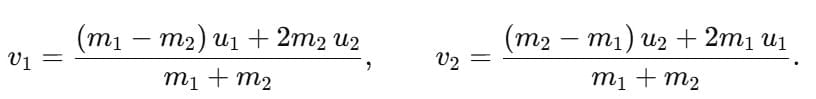
- When masses of two colliding bodies are equal, then after the collision, the bodies exchange their velocities.
v1 = u2 and v2 = u1 - If the second body of same mass (m1 = m2) is at rest, then after collision first body comes to rest and second body starts moving with the initial velocity of the first body.
v1 = 0 and v2 = u1 - If a light body of mass m1 collides with a very heavy body of mass m2 at rest, then after a collision.
v1 = – u1 and v2 = 0
It means the light body will be rebound with its own velocity and heavy body will continue to be at rest. - If a very heavy body of mass m1 collides with a light body of mass m2(m1 > > m2) at rest, then after collision
v1 = u1 and v2 = 2u1 - Loss of kinetic energy:
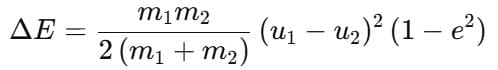 Equivalent form using reduced mass
Equivalent form using reduced mass 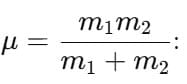
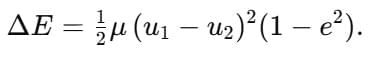
Example 1:
One sphere collides with another sphere of the same mass at rest inelastically. If the coefficient of restitution is , the ratio of their speeds after the collision is:
(a)
(b)
(c)
(d)
Sol: (c) 1 : 3
Explanation:
Let masses be equal: m1 = m2 = m, initial velocities: u1 = u, u2 = 0. After the collision, the speeds are v1 and v2.
Momentum: 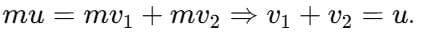
Restitution: 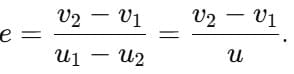
Solving, we get v2 = 1 + e2 u, v1 = 1 − e2 u.
Therefore, 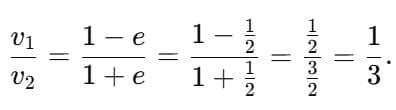
Perfectly Inelastic One-Dimensional Collision
In such types of collisions, the bodies move independently before the collision but after the collision, they move as one single body.
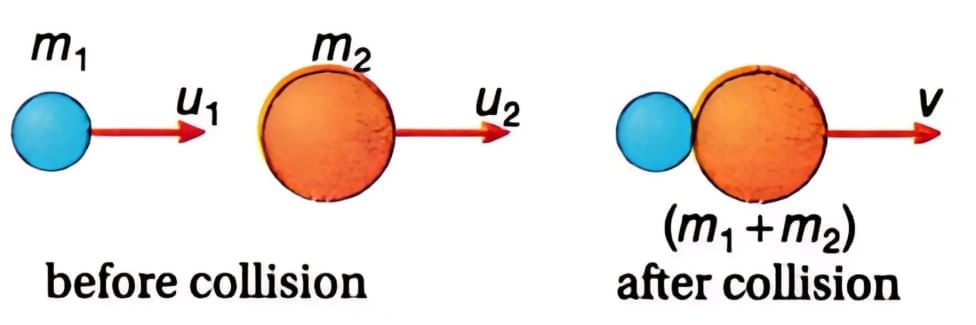
(i) When the colliding bodies are moving in the same direction:
By the law of conservation of momentum: 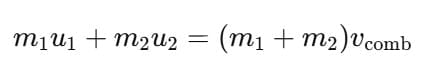
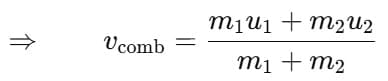
Loss in kinetic energy:
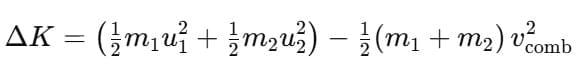
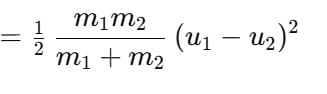
(ii) When the colliding bodies are moving in the opposite direction:
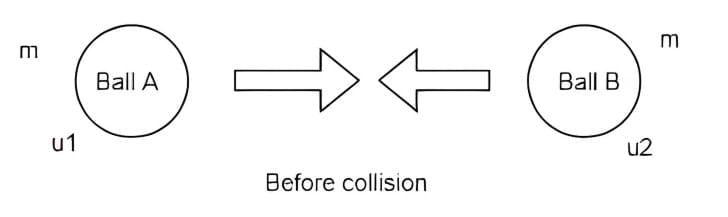
By the law of conservation of momentum:
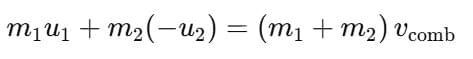
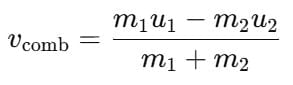
When m1u1 > m2u2, then vcomb > 0 (positive), i.e., the combined body moves along the direction of motion of mass m1.
When m1u1 < m2u2, then vcomb < 0, i.e., the combined body moves opposite to the motion of mass m1.
Loss in kinetic energy:
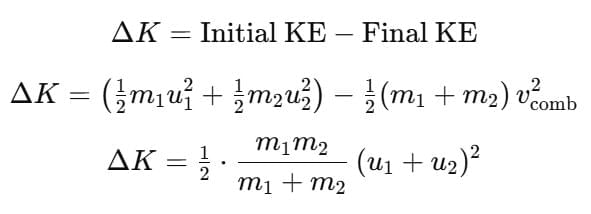 Example 2: A body of mass 2 kg is placed on a horizontal frictionless surface. It is connected to one end of a spring whose force constant is 250 N/m. The other end of the spring is joined with the wall. A particle of mass 0.15 kg moving horizontally with speed v sticks to the body after collision. If it compresses the spring by 10 cm, the velocity of the particle is
Example 2: A body of mass 2 kg is placed on a horizontal frictionless surface. It is connected to one end of a spring whose force constant is 250 N/m. The other end of the spring is joined with the wall. A particle of mass 0.15 kg moving horizontally with speed v sticks to the body after collision. If it compresses the spring by 10 cm, the velocity of the particle is
(a) 3 m/s
(b) 5 m/s
(c) 10 m/s
(d) 15 m/s
Sol: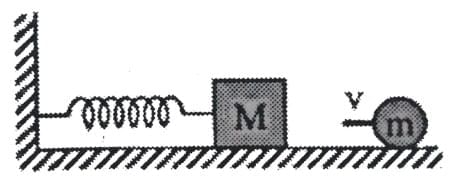
By the conservation of momentum:
Initial momentum of particle = Final momentum of system
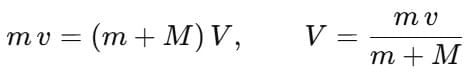
By conservation of energy (spring compression comes from kinetic energy of the system):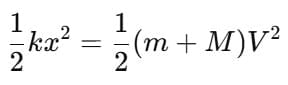
Substituting 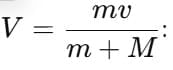
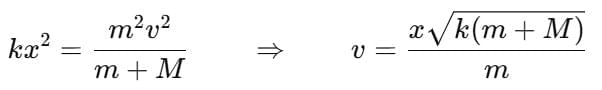
Putting values 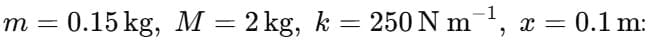
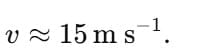
Perfectly Elastic Head on Collision
Let two bodies of masses m1 and m2 moving with initial velocities u1 and u2 in the same direction and they collide such that after collision their final velocities are v1 and v2 respectively.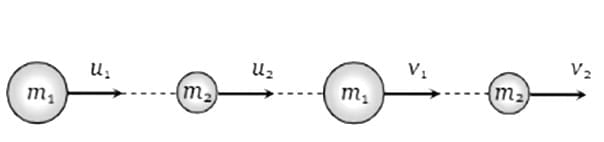
According to the law of conservation of momentum:
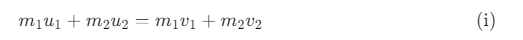
This implies:
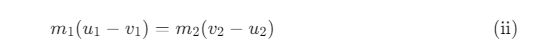
According to the law of conservation of kinetic energy:
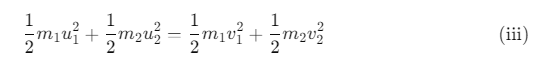
This implies:
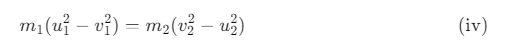
Dividing equation (iv) by equation (ii):

This implies:

Further, from equation (v) we get:
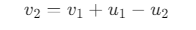
Substituting this value of v2 in equation (i) and rearranging, we get:
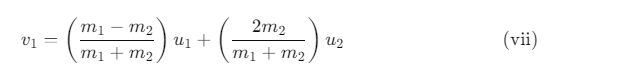
Similarly, we get:
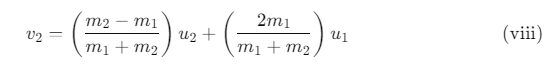
Special cases of Head on Elastic Collision
(i) If projectile and target are of the same mass i.e. m1 = m2
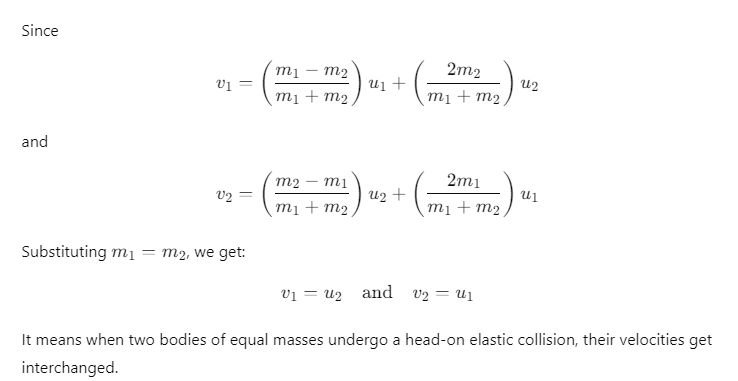
(ii) If a massive projectile collides with a light target, i.e. m1 >> m2
Since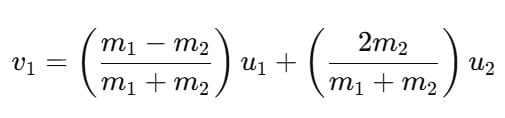
and
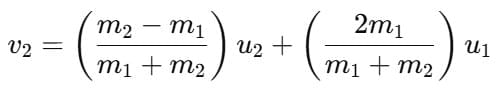
Substituting m2 = 0, we get:
v1 = u1 and v2 = 2u1 − u2
Sub case: u2 = 0, i.e. the target is at rest.
Example: Collision of a truck with a cyclist.

(iii) If a light projectile collides with a very heavy target, i.e. m₁ << m₂:
For the velocities after the collision, we have:
v1 = −u1 + 2u2
v2 = u2
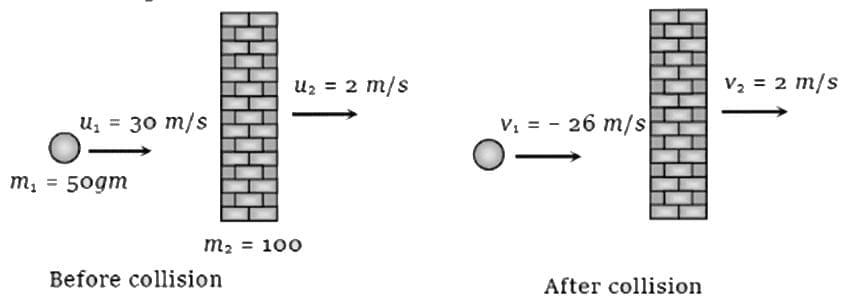
Example: Collision of a ball with a massive wall.
Before collision: The ball of mass m1 = 50 gm is moving with velocity u1 = 30 m/s, and the wall is stationary.
After collision: The ball rebounds with velocity v1 = −26 m/s, and the wall remains stationary with v2 = 2 m/s.
Sub case:
If u2 = 0 (i.e., the target is at rest), then v1 = −u1 and v2 = 0.
This means the ball rebounds with the same speed in the opposite direction when the target is stationary.
Example 3:
Assertion (A): In an elastic collision of two billiard balls, the total kinetic energy is conserved during the short time of collision of the balls (i.e., when they are in contact).
Reason (R): Energy spent against friction does not follow the law of conservation of energy.
(a) Both A and R are true, and R is a correct explanation of A
(b) Both A and R are true, but R is not a correct explanation of A
(c) A is true, but R is false
(d) Both A and R are false
Sol: (d) Both A and R are false
Explanation:
(i) When they are in contact, some part of the kinetic energy may convert into potential energy, so it is not conserved during the short time of collision.
(ii) The law of conservation of energy is always true.
Two-Dimensional or Oblique Collision
If the initial and final velocities of colliding bodies do not lie along the same line, then the collision is called two dimensional or oblique Collision.
In horizontal direction,
m1u1 cos α1 + m2u2 cos α2= m1v1 cos β1 + m2v2 cos β2
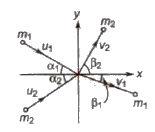
In vertical direction.
m1u1 sin α1 – m2u2 sin α2 = m1u1 sin β1 – m2u2 sin β2
If m1 = m2 and α1 + α2 = 90°
then β1 + β2 = 90°
If a particle A of mass m1 moving along z-axis with a speed u makes an elastic collision with another stationary body B of mass m2
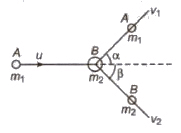
From conservation law of momentum,
m1u = m1v1 cos α + m2v2 cos β
sin β2v2 sin α – m1v1O = m
Example 4 : Three particles A, B, and C of equal mass are moving with the same velocity v along the medians of an equilateral triangle. These particles collide at the center G of the triangle. After the collision, A becomes stationary, B retraces its path with velocity v, then the magnitude and direction of the velocity of C will be:
(a) v and opposite to B
(b) v and in the direction of A
(c)
(d) v and in the direction of B
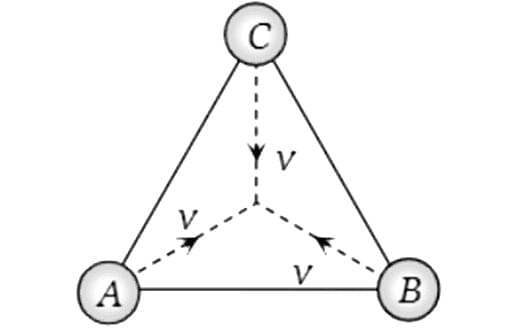
Sol:
From the figure (I), it is clear that before the collision, the initial momentum of the system is zero.
After the collision, A becomes stationary, B retraces its path with velocity v. Let C move with velocity V making an angle θ from the horizontal. As the initial momentum of the system is zero, therefore horizontal and vertical momentum after the collision should also be equal to zero.
From figure (II):
Horizontal momentum: v cosθ + v cos30∘ = 0 ……(i)
Vertical momentum: v sinθ − v sin30∘ = 0 ……(ii)
By solving (i) and (ii), we get θ = −30∘ and V = v, i.e., C will move with velocity v in the direction of B.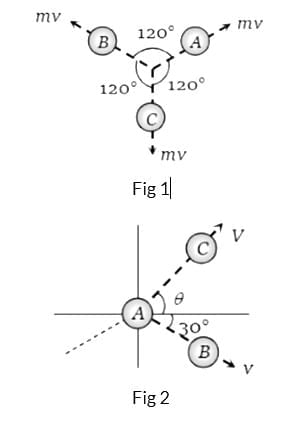
|
96 videos|367 docs|98 tests
|
FAQs on Collisions - Physics Class 11 - NEET
| 1. What are the main types of collisions in physics? |  |
| 2. How do you calculate the momentum before and after a collision? |  |
| 3. What is the difference between elastic and inelastic collisions? |  |
| 4. How does momentum conservation apply to collisions? |  |
| 5. What are real-life examples of collisions? |  |





















