NCERT Exemplar: Kinetic Theory - 2 - NEET PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.1.The container shown in Figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2= 3.0 litre. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium. Ans. V1 = 2.0 litre V2 = 3.0 litre
Ans. V1 = 2.0 litre V2 = 3.0 litre
µ1 = 4.0 moles µ2 = 5.0 moles
P1 = 1.00 atm P2 = 2.00 atm
P1V1 = µ1RT1
P2V2 = µ2 RT2
µ = µ1 + µ2
V = V1 V2
For 1 mole PV = 2/3 E
For µ1 moles 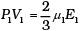
For µ2 moles 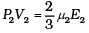
Total energy is 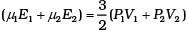
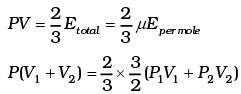
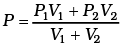
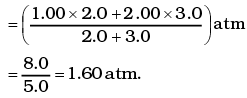
This form of ideal gas law represented by Equation marked becomes very useful for adiabatic changes.
Q.2. A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of (a) average K.E., (b) rms speeds.
Ans. The average K.E will be the same as conditions of temperature and pressure are the same
vrms α 1/√m
∵ mA > mB > mC
vC > vB > vA
Q.3. We have 0.5 g of hydrogen gas in a cubic chamber of size 3 cm kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of 100 atm. Is one justified in assuming the ideal gas law, in the final state?
(Hydrogen molecules can be consider as spheres of radius 1 Å).
Ans. We have 0.25 × 6 × 1023 molecules, each of volume 10-30m3.
Molecular volume = 2.5 × 10-7m3
Supposing Ideal gas law is valid.
Final volume 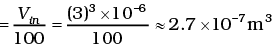
which is about the molecular volume. Hence, intermolecular forces cannot be neglected. Therfore the ideal gas situation does not hold.
Q.4. When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle’s law in this case?
Ans. According to Boyle’s law; at a constant temperature the volume of gas is inversely proportional to pressure i.e. It is valid only for constant mass of gas. But in this case when air is pumped continuously in tyre, so number of moles of air increases. So Boyle’s or gas laws does not valid in this case.
Q.5. A ballon has 5.0 g mole of helium at 7°C. Calculate
(a) the number of atoms of helium in the balloon,
(b) the total internal energy of the system.
Ans. For gas helium n = 5 mole
T = 7 + 273 = 280 K
(a) Number of atoms of he is 5 mole = 5 x 6.023 x 1023 atoms
= 30.115 x 1023 atoms
= 3.0115 x 1024 He atoms.
(b) He atom is mono atomic so degree of freedom is 3 So average kinetic energy
= 3/2 KBT Per molecule
= 3/2 KBT x Number of He Atom
= 3/2 x 1.38 x 10-23 x 280 x 3.0115 x 1024
Total E of 15 mole of He = 1.74 x 104 J
Q.6. Calculate the number of degrees of freedom of molecules of hydrogen in 1 cc of hydrogen gas at NTP.
Ans. Volume occupied by 1 gram mole of gas at NTP = 22400cc
∴ Number of molecules in 1 cc of hydrogen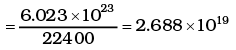
As each diatomic molecule has 5 degrees of freedom, hydrogen being diatomic also has 5 degrees of freedom
∴ Total no of degrees of freedom = 5 × 2.688 × 1019 = 1.344 x 1020
Q.7. An insulated container containing monoatomic gas of molar mass m is moving with a velocity vo. If the container is suddenly stopped, find the change in temperature.
Ans. Loss in K.E of the gas = ΔE = 1/2(mn)v02
where n = no: of moles.
If its temperature changes by ∆T , then
= n(3/2)RΔT
= 1/2mn v02.
∴ ΔT = 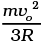
LONG ANSWER TYPE QUESTIONS
Q.1. Explain why
(a) there is no atmosphere on moon.
(b) there is fall in temperature with altitude.
Ans. The moon has small gravitational force and hence the escape velocity is small. As the moon is in the proximity of the Earth as seen from the Sun, the moon has the same amount of heat per unit area as that of the Earth. The air molecules have large range of speeds. Even though the rms speed of the air molecules is smaller than the escape velocity on the moon, a significant number of molecules have speed greater than escape velocity and they escape. Now rest of the molecules arrange the speed distribution for the equilibrium temperature. Again a significant number of molecules escape as their speeds exceed escape speed. Hence, over a long time the moon has lost most of its atmosphere.
At 300 K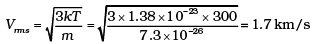
Vesc for moon = 4.6 km/s
(b) As the molecules move higher their potential energy increases and hence kinetic energy decreases and hence temperature reduces.
At greater height more volume is available and gas expands and hence some cooling takes place.
Q.2. Consider an ideal gas with following distribution of speeds.
| Speed (m/s) | % of molecules |
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(i) Calculate Vrms and hence T. (m = 3.0× 10−26 kg)
(ii) If all the molecules with speed 1000 m/s escape from the system, calculate new Vrms and hence T.
Ans. (This problem is designed to give an idea about cooling by evaporation)
(i) 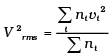
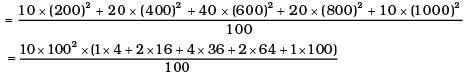
= 1000 × (4 + 32 + 144 +128 + 100) = 408 ×1000 m2/s2
∴ vrms = 639 m/s
= 2.96 ×102K = 296K
(ii) 
vrms = 584 m/s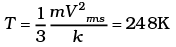
Q.3. Ten small planes are flying at a speed of 150 km/h in total darkness in an air space that is 20 × 20 × 1.5 km3 in volume. You are in one of the planes, flying at random within this space with no way of knowing where the other planes are. On the average about how long a time will elapse between near collision with your plane. Assume for this rough computation that a saftey region around the plane can be approximated by a sphere of radius 10m.
Ans. Planes can be considered as the motion of molecules in confined space. Time of relaxation for mean free path λ is distance between two planes travelled between the collision or just to avoid accident.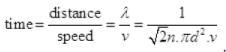
N = number of particles per unit volume V = N/Volume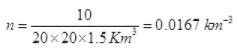
d = 2 x 10 m = 20 m = 20 x 10-3 km, v = 150 Km/hr
∴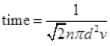
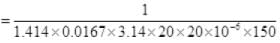
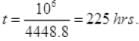
Q.4. A box of 1.00m3 is filled with nitrogen at 1.50 atm at 300K. The box has a hole of an area 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.
Ans. Volume of box = 1m3 =V1
Initial pressure = 1.5 atm = P1
Final pressure = 1.5 – 0.1 = 1.4 atm =P’2
Air pressure out side box = P2 = 1 atm
Initial temperature T1 = 300K
Final temperature T2 = 300K
a = area of hole = 0.01 mm2 = 0.01 x 10-6 m2 = 10-8 m2
initial pressure difference between tyre and atmosphere ΔP = (1.5 - 1)atm
mass of a N2 gas molecule = 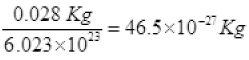
KB = 1.38 x 10-23
Let Pn1 is the initial number of N2 gas molecule per unit volume in time Δt Let vix is the speed of molecules along x axis
Number of molecule colliding in time Δt on a wall of cube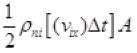
1/2 is multiplied as other 1/2 molecule will strike to opposite wall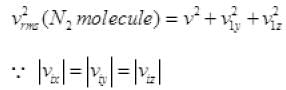
Then 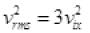
KE of gas molecule = 3/2 KBT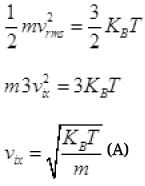
Number of N2 gas molecule striking to a wall in Δt time Outward = 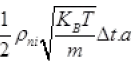 out
out
Temperature inside the box and air are equal to T
The number of air molecule striking to hole in Δt
inward = 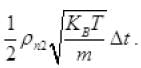 a inward
a inward
ρn2 = density of air molecule
Net number of molecule (going outward)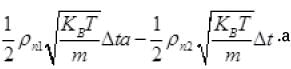
Net number of molecules going out from hole in Δt time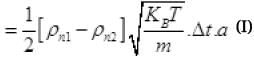
Gas equation 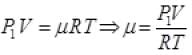
As for box 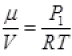 (μ = No. of moles of gas in box)
(μ = No. of moles of gas in box)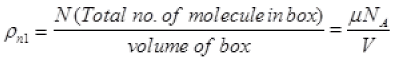
= P1NA/RT Per unit volume
Let after time T pressure reduced by 0.1 and becomes (1.5 - 1) = 1.4 atm P'2
Then final new density of NA molecule ρ'n1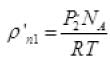 Per unit volume (III)
Per unit volume (III)
Net number of molecules going out from volume V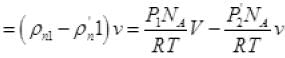
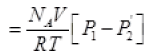 (iv) (from II, III)
(iv) (from II, III)
P2 = final pressure of box
From (I) total number of molecule going out in time τ from hole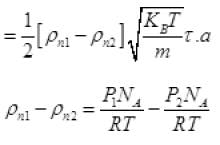
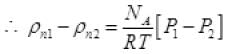 (P2 = Press of air out of box)
(P2 = Press of air out of box)
Net number of molecule going out in τ time from above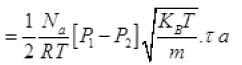
From (V) and IV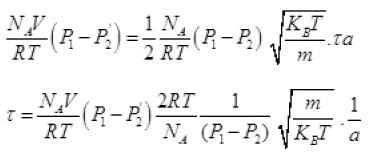
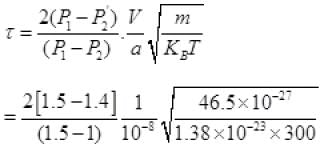
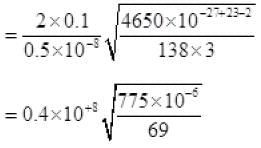
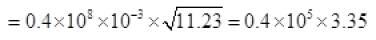
τ = 1.34 x 105 seconds
Q.5. Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density ρ. Assume the velocity is along x-axis and the area of cross-section of the block perpendicular to v0 is A. Show that the drag force on the block is 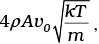 where m is the mass of the gas molecule.
where m is the mass of the gas molecule.
Ans. n = no. of molecules per unit volume
vrms = rms speed of gas molecules
When block is moving with speed vo, relative speed of molecules w.r.t. front face = v + vo
Coming head on, momentum transferred to block per collission
= 2m (v+vo), where m = mass of molecule.
No. of collission in time 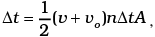 where A = area of cross section of block and factor of 1/2 appears due to particles moving towards block.
where A = area of cross section of block and factor of 1/2 appears due to particles moving towards block.
∴ Momentum transferred in time Δt = m(v + v0)2 nAΔt from front surface
Similarly momentum transferred in time Δt = m(v + v0)2 nAΔt from back surface
∴ Net force (drag force) = mnA[(v + v0) - (v - v0)2] from front
= mnA (4vvo) = (4mnAv)vo
= (4ρAv)vo
We also have 1/2 mv2 = 1/2kT (v - is the velocity along x-axis)
Therefore, 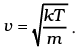
Thus drag 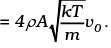
FAQs on NCERT Exemplar: Kinetic Theory - 2 - NEET
| 1. What is the kinetic theory of matter? |  |
| 2. How does the kinetic theory explain the different states of matter? |  |
| 3. What are the assumptions of the kinetic theory? |  |
| 4. How does temperature affect the kinetic energy of particles? |  |
| 5. What is the relationship between pressure and temperature in gases according to the kinetic theory? |  |














