Mechanical Properties of Fluids: Part 1 | Science & Technology for UPSC CSE PDF Download
Fluid Mechanics
- Fluid mechanics deals with the behaviour of fluids at rest and in motion. A fluid is a substance that deforms continuously under the application of a shear (tangential) stress no matter how small the shear stress may be.
- Thus, fluids comprise the liquid and gas (or vapor) phase of the physical forms in which matter exists.
 Fluid
Fluid
Terms Related to Fluids
Density (r):
Mass of unit volume, Called density
Density at a point of liquid described by
density is a positive scalar quantity
SI unit = Kg/m3
CGS unit = gm/cm3
Dimension = [ML-3]
Relative Density:
It is the ratio of density of the given liquid to the density of pure water at 4°C
Relative density or specific gravity is unitless, dimensionless. It is a positive scalar physical Quantity.
Value of R.D. is same in SI and CGS system due to dimensionless/unitless
Specific Gravity:
It is the ratio of the weight of given liquid to the weight of pure water at 4°C
Specific Gravity = =
= Relative density of liquid i.e. than the specific gravity of a liquid is approximately equal to the relative density. For calculation, they can be interchanged
Pressure in a Fluid
- When a fluid (either liquid or gas) is at rest, it exerts a force perpendicular to any surface in contacts with it, such as a container wall or a body immersed in the fluid.
- While the fluid as a whole is at rest, the molecules that make up the fluid are in motion, the force exerted by the fluid is due to molecules colliding with their surroundings.
- If we think of an imaginary surface within the fluid, the fluid on the two sides of the surface exerts equal and opposite forces on the surface, otherwise, the surface would accelerate and the fluid would not remain at rest.
- Consider a small surface of area dA centered on a point on the fluid, the normal force exerted by the fluid on each side is
. The pressure P is defined at that point as the normal force per unit area, i.e.,
- If the pressure is the same at all points of a finite plane surface with area A, then
- where
is the normal force on one side of the surface. The SI unit of pressure is the pascal, where
1 pascal = 1 Pa = 1.0 N/m2 - One unit used principally in meteorology is the Bar which is equal to 105 Pa.
1 Bar = 105 Pa
Atmospheric Pressure (P0)
It is the pressure of the earth's atmosphere. This changes with weather and elevation. Normal atmospheric pressure at sea level (an average value) is 1.013 × 105 Pa. Thus
1 atm = 1.013 × 105 Pa
Note: Fluid pressure acts perpendicular to any surface in the fluid no matter how that surface is oriented. Hence, pressure has no intrinsic direction of its own, its a scalar. By contrast, force is a vector with a definite direction.
Pascal's Law
- According to Pascal's Law, the external static pressure applied to a confined liquid is distributed evenly throughout the liquid in all directions.
- The static pressure acts at right angles to any surface that comes into contact with the fluid.
- Pascal discovered that the pressure at a specific point in a static fluid remains the same across all planes that pass through that point within the fluid.
- Pascal's law is also referred to as Pascal's principle or the principle of transmission of fluid-pressure.
- This law was first articulated by the French mathematician Blaise Pascal in 1653.
Pascal Law Formula
Following is the formula of Pascal law: F = PA
Where,
F is the force applied,
P is the pressure transmitted, and
A is the cross-sectional area.
Example of Pascal's Law
Let's explore how Pascal's law works with an example.
- A pressure of 2000 Pa is applied to a liquid column because of a force on a piston.
- If the piston area is 0.1 m2, we can find the force applied using Pascal's Law formula:
- F = PA
- In this formula:
- P = 2000 Pa = N/m2
- A = 0.1 m2
- By putting the values into the formula, we get:
- F = 200 N
Applications of Pascal's Law
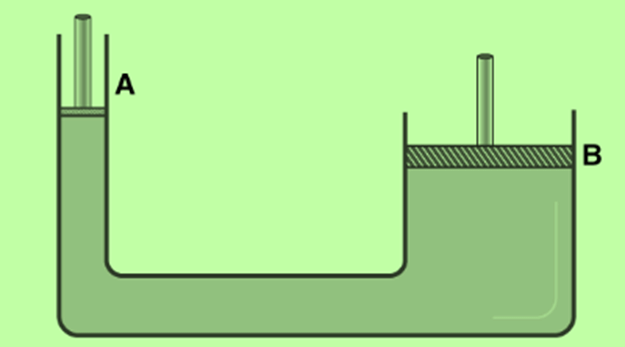
- Hydraulic Lift: The first image in this article shows a basic diagram of a hydraulic lift. This device operates based on the principle of equal pressure transmission in a fluid, as stated by Pascal's Law.
- The lift consists of a narrow cylinder (Cylinder A) connected to a wider cylinder (Cylinder B). Both ends are fitted with airtight pistons.
- These cylinders are filled with an incompressible fluid.
- When pressure is applied to piston A, it is transmitted equally to piston B without losing any fluid. This allows piston B to lift heavy objects, such as large machines or vehicles.
- Other uses of Pascal's Law include:
- Hydraulic Jack
- Hydraulic Press
- Braking Systems in most cars use forced amplification based on this principle.
Pascal's Law Derivation
- Consider a right-angled prismatic triangle located in a liquid with a density of rho.
- Because the prismatic shape is very small, every point within it can be regarded as being at the same level as the surface of the liquid.
- As a result, the pressure T is uniform at all these points.
- The influence of gravity is also consistent across these points due to the small size of the prismatic element.
- This uniformity of pressure and gravitational effect is crucial for understanding the principles of Pascal's Law.

Let ad, bd, and cd represent the area of the faces ABFE, ABDC, and CDFE, respectively.
Let P1, P2, and P3 denote the pressure acting on the faces ABFE, ABDC, and CDFE.
Pressure creates a force that acts perpendicular to the surface.
Let P1 create a force F1 on the surface ABFE.
Let P2 create a force F2 on the surface ABDC.
Let P3 create a force F3 on the surface CDFE.
Therefore, the forces can be expressed as:
- F1 = P1 × area of ABFE = P1ad
- F2 = P2 × area of ABDC = P2bd
- F3 = P3 × area of CDFE = P3cd
Also, 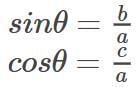
Additionally, the total force on the prism will be zero because the prism is stable.
- The relationships between the forces are:
- F1 sin θ = F2
- F1 cos θ = F3
- From these equations, we find:
- P1 ad b/a = P2 bd (equation 1)
- P1ad c/a = P3 cd (equation 2)
- By solving equations 1 and 2, we conclude that:
- P1 = P2
- P1 = P3
- Thus, it follows that P1 = P2 = P3.
Variation in Pressure with depth
- If the weight of the fluid can be neglected, the pressure in a fluid is the same throughout its volume. But often the fluid's weight is not negligible and under such condition, pressure increases with increasing depth below the surface.
- Let us now derive a general relation between the pressure P at any point in a fluid at rest and the elevation y of that point. We will assume that the density r and the acceleration due to gravity g are the same throughout the fluid. If the fluid is in equilibrium, every volume element is in equilibrium.
- Consider a thin element of fluid with height dy. The bottom and top surfaces each have area A, and they are at elevations y and y + dy above some reference level where y = 0. The weight of the fluid element is
dW = (volume) (density) (g) = (A dy) (r) (g)
or dW = rg A dy - What are the other forces in y-direction of this fluid element? Call the pressure at the bottom surface P, the total y component of upward force is PA. The pressure at the top surface is P dP and the total y-component of downward force on the top surface is (P dP) A. The fluid element is in equilibrium, so the total y-component of force including the weight and the forces at the bottom and top surfaces must be zero.
åFy = 0
PA -(P + dP) A -rgAdy = 0
or...(i)
This equation shows that when y increases, P decreases, i.e., as we move upward in the fluid, pressure decreases.
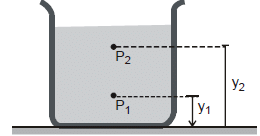
- If P1 and P2 be the pressures at elevations y1 and y2 and if r and g are constant, then integrating Eq.(i), we get
or P2 -P1 = -rg (y2 -y1) ...(ii) - It's often convenient to express Eq. (ii) in terms of the depth below the surface of a fluid. Take point 1 at depth h below the surface of fluid and let P represents pressure at this point. Take point 2 at the surface of the fluid, where the pressure is P0 (subscript zero for zero depth). The depth of point 1 below the surface is,
h = y2 -y1
and Eq. (ii) becomes
P0 -P = -rg (y2 -y1) = -rgh
P = P0 rgh ...(iii)
Thus, pressure increases linearly with depth, if r and g are uniform, A graph between P and h is shown below.
Further, the pressure is the same at any two points at the same level in the fluid. The shape of the container does not matter.
Barometer
It is a device used to measure atmospheric pressure.
In principle, any liquid can be used to fill the barometer, but mercury is the substance of choice because its great density makes possible an instrument of reasonable size.
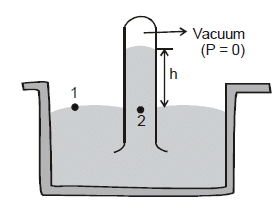
P1 = P2
Here, P1 = atompsheric pressure (P0)
and P2 = 0 + pgh = pgh
Here, p = density of mercury
p0 = pgh
Thus, the mercury barometer reads the atmosphereic pressure (P0) directly from the height of the mercury column.
For example if the height of mercury in a barometer is 760 mm, then atmospheric pressure will be,
P0 = rgh = (13.6 × 103) (9.8) (0.760)= 1.01 × 105 N/m2
 Barometer
Barometer
Force on Side Wall of Vessel
Force on the sidewall of the vessel can not be directly determined as at different depths pressures are different. To find this we consider a strip of width dx at a depth x from the surface of the liquid as shown in figure,
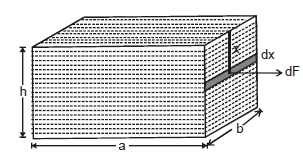
and on this strip the force due to the liquid is given as:
dF = xrg × bdx
This force is acting in the direction normal to the sidewall.
Net force can be evaluated by integrating equation
...(2.4)
Average Pressure on Side Wall
The absolute pressure on the sidewall cannot be evaluated because at different depths on this wall pressure is different. The average pressure on the wall can be given as :
=
...(2.5)
Equation (2.5) shows that the average pressure on side vertical wall is half of the net pressure at the bottom of the vessel.
Torque on the Side Wall due to Fluid Pressure
As shown in figure, due to the force dF, the sidewall experiences a torque about the bottom edge of the side which is given as
= xrgb dx (h -x)
This net torque is
Manometer
It is a device used to measure the pressure of a gas inside a container.
 Manometer
Manometer
The U-shaped tube often contains mercury.
P1 = P2
Here, P1 = pressure of the gas in the container (P)
and P2 = atmospheric pressure (P0) + rgh
P = P0 hrg
This can also be written as
P -P0 = gauge pressure = hrg
Here, r is the density of the liquid used in U - tube
Thus by measuring h we can find absolute (or gauge) pressure in the vessel.
Example 1. Two liquid which do not react chemically are placed in a bent tube as shown in figure. Find out the displacement of the liquid in equilibrium position.
Sol. The pressure at the interface must be same, calculated via either tube. Since both tube all open to the atmosphere, we must have.
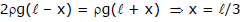
Example 2. Three liquid which do not react chemically are placed in a bent tube as shown in figure (initially) then fluid out the displacement of the liquid in equilibrium position.
Sol. Let us assume that level of liquid having density 3r displaced below by x as shown in figure below.
⇒ 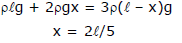
Pressure Distribution in an Accelerated Frame
We've already discussed that when a liquid is filled in a container, generally its free surface remains horizontal as shown in figure (a) as for its equilibrium its free surface must be normal to gravity i.e. horizontal. Due to the same reason we said that pressure at every point of a liquid layer parallel to its free surface remains constant. Similar situation exist when liquid is in an accelerated frame as shown in figure (b). Due to acceleration of container, liquid filled in it experiences a pseudo force relative to container and due to this the free surface of liquid which normal to the gravity now is filled as:
...(2.22)
Now from equilibrium of liquid we can state that pressure at every point in a liquid layer parallel to the free surface (which is not horizontal), remains same for example if we find pressure at a point A in the accelerated container as shown in figure (a) is given as

Where h is the depth of the point A below the free surface of liquid along effective gravity and P0 is the atmospheric pressure acting on free surface of the liquid.
The pressure at point A can also obtained in an another way as shown in figure (b). If l1 and l2 are the vertical and horizontal distances of point A from the surface of liquid then pressure at point A can also be given as
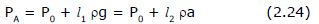
Here l1rg is the pressure at A due to the vertical height of liquid above A and according to Pascal's Law pressure at A is given as
...(2.25)
Here we can write l1 as
or from equation (2.25)
Similarly if we consider the horizontal distance of point A from free surface of liquid, which is l2 then due to pseudo acceleration of container the pressure at point A is given as
...(2.26)
Here l2 is given as
From equation (2.24), we have
Here students should note that while evaluating pressure at point A from vertical direction we haven't mentioned any thing about pseudo acceleration as along vertical length l1, due to pseudo acceleration at every point pressure must be constant similarly in horizontal direction at every point due to gravity pressure remains constant.
Example 3. Figure shows a tube in which liquid is filled at the level. It is now rotated at an angular frequency w about an axis passing through arm A find out pressure difference at the liquid interfaces.
Sol. To solve the problem we take a small mass dm from the axis at `a' distance x in displaced condition.
Net inward force = (P +dP) A -PA
= AdP
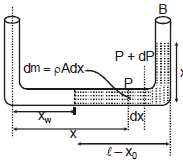
This force is balanced by centripetal force in equilibrium
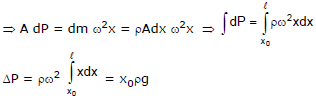
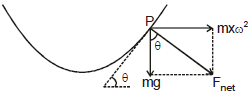
Example 4. A liquid of density r is in a bucket that spins with angular velocity w as shown in figure.

Show that the pressure at a radial distance r from the axis is
where P0 is the atmospheric pressure.
Sol. Consider a fluid particle P of mass m at coordinates
(x, y). From a non-inertial rotating frame of reference two forces are acting on it,
(i) pseudo force (mxw2)
(ii) weight (mg)
in the directions shown in figure.
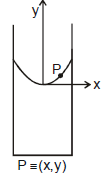
The net force on it should be perpendicular to the free surface (in equilibrium). Hence.
or
This is the equation of the free surface of the liquid, which is a parabola.
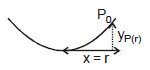
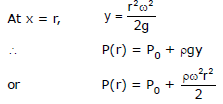
|
90 videos|491 docs|209 tests
|
FAQs on Mechanical Properties of Fluids: Part 1 - Science & Technology for UPSC CSE
| 1. What is atmospheric pressure and how is it measured? |  |
| 2. How does pressure vary with depth in a fluid? |  |
| 3. What is a manometer and how is it used to measure pressure? |  |
| 4. What is the force exerted on the side walls of a vessel containing fluid? |  |
| 5. How does pressure distribution behave in an accelerated frame? |  |

















