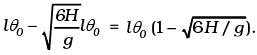NCERT Exemplar: Oscillations - 2 - NEET PDF Download

SHORT ANSWER TYPE QUESTIONS

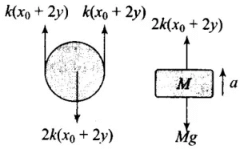
Q.1. Find the time period of mass M when displaced from its equilibrium positon and then released for the system shown in Figure.

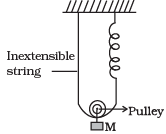
Ans. For observing oscillation, we have to displace the block slightly beyond equilibrium position and find the acceleration due to the restoring force.
Let in the equilibrium position, the spring has  extended by an amount x₀. 
Tension in the spring = kx₀ 
For equilibrium of the mass M, Mg = 2kx₀ 

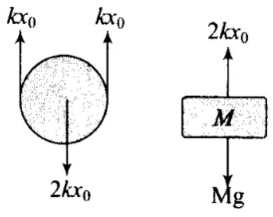
Let the mass be pulled through a distance y and then released. But, string is inextensible, hence the spring alone will contribute the total extension y + y = 2y, to lower the mass down by y from initial equilibrium mean position x₀. So, net extension in the spring (x₀ + 2y). From F.B.D of the block, 
2k (x₀ + 2y) - Mg = Ma
2kx₀ + 4ky - Mg = Ma ⇒ Ma = 4ky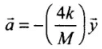

K and M being constant.
∴ a ∝ -x. Hence, motion is SHM
Comparing the above acceleration expression with standard SHM equation a = -ω²x, we get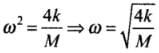


Q.2. Show that the motion of a particle represented by y = sin ω t - cos ω t is simple harmonic with a period of 2π/ω.
Ans. A function will represents S.H.M. if it can be written uniquely in the form of a or a sin (2π/T (t+ϕ))
Now y = sinωt - cosωt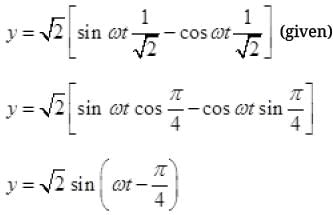

Comparing with standard SHM y = a s sin (2π/T(t+ϕ))
We  get w = 2π/T or T = 2π/ω.

Q.3. Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
Ans. Let us assume that the required displacement where PE is half of the maximum energy of the oscillator be x.
The potential energy of the oscillator at this position,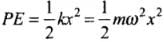
 ...(i)
Maximum energy of the oscillator = Maximum potential energy = Total energy
TE = 1/2 mω²A² ...(ii)
where, A = amplitude of motion
We are given, PE = 1/2 TE
⇒
⇒

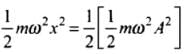
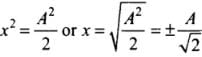
Q.4. A body of mass m is situated in a potential field U(x) = U₀ (1-cos αx) when U₀ and α are constants. Find the time period of small oscillations.
Ans. U = U₀ (1 - cosα x)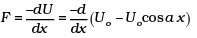

= -U₀ α sin α x
= -U₀ ααx (for small αx, sin αx - αx)
= -U₀α²x
We know that F = -kx
So, k = U₀α²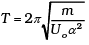


Q.5. A mass of 2 kg is attached to the spring of spring constant 50 Nm^–1. The block is pulled to a distance of 5cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
Ans. x = 5 sin 5t

Q.6. Consider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2° to the right with the vertical, the other pendulum makes an angle of 1° to the left of the vertical. What is the phase difference between the pendulums?
Ans.  θ₁ = θ₀ sin(ωt + δ₁)
θ₂ = θ₀ sin ((ωt + δ₂)
For the first, θ = 2°, ∴ sin (ωt + δ₁) = 1
For the 2nd, θ = -1°, ∴ sin (ωt + δ₂) = -1/2
∴ ωt + δ₁ = 90°, ωt + δ₂ = -30°
∴ δ₁ - δ₂ = 120°

LONG ANSWER TYPE QUESTIONS

Q.1. A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s^-1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
(a) Will there be any change in weight of the body, during the oscillation?
(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
Ans. (a) Weight in weight machine will be due to the normal reaction (N) by platform. Consider the top position of platform, two forces due to weight of person and oscillator acts both downward.

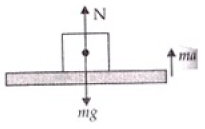
So motion is downward. Let with acceleration a then
ma = mg - N ...(i)
When platform lifts form its lowest position to upward
ma = N - mg ...(ii)
a = ω²A acceleration of oscillator
(i) ∴ Form (i) equation
N = mg - mω²A
Where A is amplitude, ω angular frequency, m mass of oscillator.
ω = 2πv = 2π x 2 = 4π rad/sec.
A = 5 cm = 5 x 10^-2 m, m = 50 kg
N = 50 x  9.8 - 50 x 4π x 4π x 5 x 10^-2
= 50[9.8 - 16π² x 5 x 10^-2]
= 50[9.8 - 80 x 3.14 x 3.14 x 10^-2]
N = 50[9.8 - 7.89] = 50 x 1.91 = 95.50 N
So minimum weight is 95.50 N.
(ii) form (ii) N - mg = ma
For upward motion form lowest point of oscillator.
N = mg + ma = m(a+g)
= m[9.81 + ω²A] a = ω²A
= 50[9.81 + 16π² x 5 x 10^-2]
= 50[9.81 + 7.89] = 50 [ 17.70]
N = 885.00 N
(a) Hence, there is a change in weight of the body during oscillation.
(b) The maximum weight is 885 N, when platform moves from lowest to upward direction.
And the minimum is 95.5 N, when platform moves from highest point to downward direction.

Q.2. A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
Ans. (a) when mass m is held in support by hand the extension in spring will be zero as no deforming force acts on spring.
Let the mass reaches at its new position unit displacement from previous.
Then P.E. of spring or mass = gravitational P.E. lost by man

P.E = mg x
But P.E. due to spring is 1/2 kx²k = ω²A
∴ 1/2 kx² = mg x
x = 2mg/k
Mean position of spring by block will be when let extension is x₀ then
F = +kx₀
F= mg ∴ mg = +kx₀ or x₀ = mg/k ...(ii)
From (i) and (ii)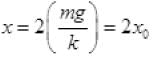

x = 4 cm ∴ 4 = 2x₀
x₀ = 2 cm.
The amplitude of oscillator is the maximum distance from mean position i.e., x - x₀ = 4 - 2 = 2 cm.
(b) Time period T = 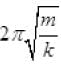 which does not depend on amplitude
2mg/k = x from (i)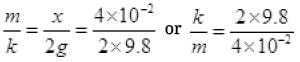



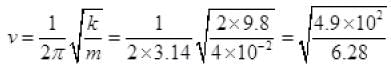
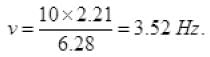
Oscillator will not rise above the positive from where it was released because total extension in spring is 4 cm when released and amplitude is 2 cm. So it oscillates below the released position.

Q.3. A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period.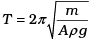

where m is mass of the body and ρ is density of the liquid.
Ans. When log is pressed downward into the liquid then and upward Buoyant force (B.F.) action it which moves the block upward and due to inertia it moves upward from its mean position due to inertia and then again come down due to gravity. So net restoring force  on block = Buoyant force – mg

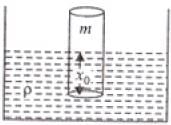
V = volume of liquid displaced by block
Let when floats then
mg = B.F. or mg = V ρg
mg = Ax₀ρg ...(i)
A = area of cross-section
x₀ = Height of block liquid
Let x height again dip in liquid when pressed into water total height of block in water = (x + x₀)
So net restoring force = [A(x+x₀)] ρ.g - mg
F_restoring = A x₀ρg + Axρg - Ax₀ρg
F_restoring = - Axpg
(as Buoyant force is upward and x is downward)
F_restoring = ∝ - x
So motion is SHM here k Aρg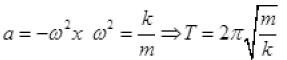

F_restoring = -Apgx
ma = - Apgx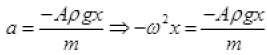


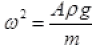
k = Aρg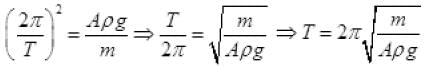


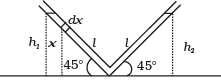
Q.4. One end of a V-tube containing mercury is connected to a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45° each. A small pressure difference is created between two columns when the suction pump is removed. Will the column of mercury in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Find the time period of oscillation.
Ans. Consider the liquid in the length dx . It’s mass is A ρdx at a height x.
PE = A ρdx gx
The PE of the left column

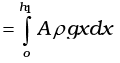
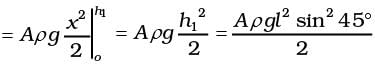
Similarly, P.E. of the right column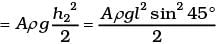
h₁ = h₂ = l sin 45° where l is the length of the liquid in one arm of the tube.
Total P.E. = Aρgh² = Aρgl² sin² 45°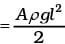
If the change in liquid level along the tube in left side in y, then length of the liquid in left side is l – y and in the right side is l + y.
Total P.E. = Aρg(l – y)² sin² 45° + Aρg(l + y)² sin² 45°
Change in PE = (PE)_f – (PE)_i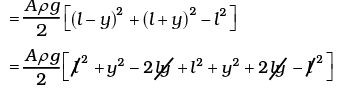

= Aρg [y² + l²]
Change in K.E. = 1/2 Aρ2ly²
Change in total energy = 0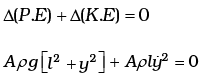

Differentiating both sides w.r.t. time,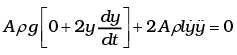

2Aρgy + 2 Aρly = 0
ly + gy = 0
y + g/l (y) = 0
ω² = g/l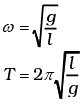


Q.5. A tunnel is dug through the centre of the Earth. Show that a body of mass ‘m’ when dropped from rest from one end of the tunnel will execute simple harmonic motion.
Ans. Acceleration due to gravity at P = g.x/R, where g is the acceleration at the surface.
Force = mgx/R = -k.x, k = mg/R
Motion will be SHM with time period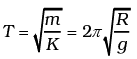

Q.6. A simple pendulum of time period 1 second and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure).  The amplitude is θ₀. The string snaps at θ = θ₀/2. Find the time taken by the bob to hit the ground. Assume θ₀ to be small so that sinθ₀ θ₀ and cosθ₀ l.

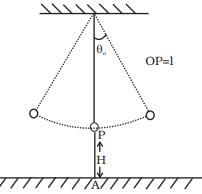
Ans. Assume that t = 0 when θ = θ₀. Then,
θ = θ₀ cos ωt
Given a seconds pendulum ω = 2π
At time t₁, let θ = θ₀/2

∴

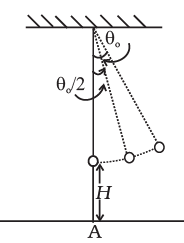
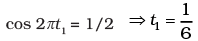
θ = -θ₀2π sin 2πt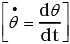  
At t₁ = 1/6
θ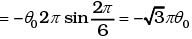
Thus the linear velocity is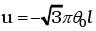
perpendicular to the string.
The vertical component is
u_y = -√3πθ₀lsinθ₀
and the horizontal component is
u_x = -√3πθ₀lcosθ₀
At the time it snaps, the vertical height is
H′ = H + l (1 – cos(θ₀/2))
Let the time required for fall be t, then
H' = u_yt + (1/2)gt² (notice g is also in the negative direction)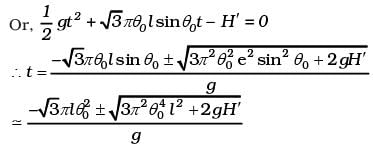

Neglecting terms of order θ²₀ and higher,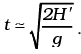

Now H' ≃ H + l (1 – 1) = H ∴ t ≈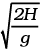
The distance travelled in the x direction is u_xt to the left of where it snapped.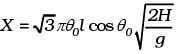

To order of θ₀,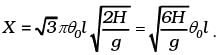

At the time of snapping, the bob was
l sinθ₀≃lθ₀ distance from A.
Thus, the distance from A is