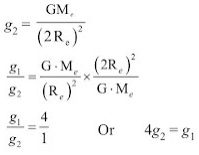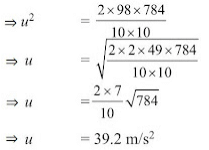Gravitation Summary Class 9 Science Chapter 9
Introduction

- Gravitational Force of Earth: If we release a small stone without pushing it from a height, it accelerates towards earth.
- The stone is when accelerated towards earth, means some force is acting on it. The force which pulls the objects towards the centre of the earth is known as gravitational force of the earth.
- Here, stone also attracts earth. It means every object in universe attracts every other object.
Newton’s Universal Law of Gravitation
- Sir Isaac Newton in 1687 proposed a law about the force of attraction between the two objects in the universe which is known as Newton’s law of gravitation.

According to Universal law of Gravitation
- Every mass in this universe attracts every other mass with a force which is directly proportional to the product of two masses and inversely proportional to the square of the distance between them.
Let masses (M) and (m) of two objects are distance (d) apart, then force of attraction (F) between them
F ∝ M×m
F ∝ 1/d2
F ∝ Mm/d2
F = (GMm)/d2
where,
G is a constant and is known as Gravitational constant.
Value of G = 6.67×10-11 Nm2/kg2
G is called universal gravitational constant. - If unit of F is in Newton, m is in kg, d is in metre, then unit of G can be calculated as :
G = (F×d2)/Mm, therefor unit will be Nm2/kg2
Relation between Newton’s third law of motion and Newton’s law of gravitation
- According to Newton’s third law of motion, “Every object exerts equal and opposite force on other object but in opposite direction.”
- According to Newton’s law of gravitation, “Every mass in the universe attracts the every other mass.”
- In case of freely falling stone and earth, stone is attracted towards earth means earth attracts the stone.
- But according to Newton’s third law of motion, the stone should also attract the earth.
It is true that stone also attracts the earth with the same force F = m × a but due to very less mass of the stone, the acceleration (a) in its velocity is 9.8 m/s2 and acceleration (a) of earth towards stone is 1.65×10-24 m/s2 which is negligible and we cannot feel it.
Importance of universal law of gravitation
- The force that binds us to the earth.
- The motion of moon around the earth.
- The motion of earth around the sun.
- The tides due to moon and the sun.
Free fall of an object and acceleration (g)
- When an object is thrown upward, it reaches certain height, then it starts falling down towards earth. It is because the earth’s gravitational force exerts on it.
- This fall under the influence of earth is called ‘free fall of an object’.
- During this free fall direction do not change but velocity continuously changes which is called acceleration due to gravity. It is denoted by ‘g’.
- Its unit is same as acceleration m/s2.
Gravitational Acceleration and its value at the surface of earth
- The uniform acceleration produced in a freely falling object due to the gravitational force of earth, is called acceleration due to gravity.
- It is represented by ‘g’ and it always acts towards the centre of the earth.
Value of ‘g’ on the surface of earth
- The force acting on an object is F = (GMem)/R2 .... (i)
where,
Me = Mass of earth
m = Mass of an object
R = Radius of earth
If acceleration due to gravity is ‘g’ due to force F then, F = m×g .... (ii)
Equating (i) and (ii), we get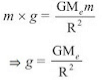
If G = 6.673 x 10-11 Nm2/kg, Me = 6 x 1024 kg, R2 = (6.37 x 106)2
Then,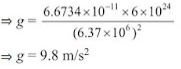
Relationship and difference between ‘G’ and ‘g’
G = Gravitational constant
g = Acceleration due to gravity
g = GM/R2
Difference between G (Gravitational constant) and g (Acceleration due to gravity)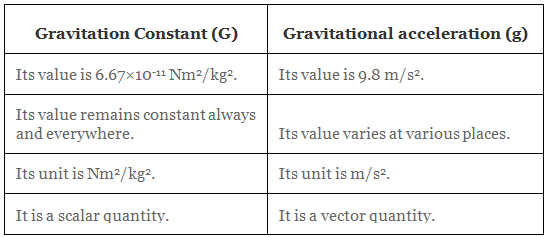
Example: If two stones of 150 gm and 500 gm are dropped from a height, which stone will reach the surface of earth first and why ? Explain your answer.
It was Galileo, who first time demonstrated and depicted that the acceleration of an object falling freely towards earth does not depend on the mass of the object.
It can be verified by universal law of gravitation. Let an object of mass m, is allowed to fall from a distance of R, from the centre of the earth.
Then, the gravitational force, F = (GMem)/R2 (Me = Mass of the earth)
The force acting on the stone is F = m×a
∴ m × a = (GMem)/R2
⇒ a = GMe/R2
So, acceleration in an object falling freely towards earth depends on the mass of earth and height of the object from the centre of the earth.
So, stones of mass 150 gm and 500 gm will reach the earth surface together.
Equation of motion when an object is falling freely towards earth or thrown vertically upwards
Case 1: When an object is falling towards earth with initial velocity (u)
Velocity (v) after t seconds, v = u + ght
Height covered in t seconds, h = ut + ½gt2
Relation between v and u when t is not given: v2 = u2 + 2gh
Case 2: When object is falling from rest position means initial velocity u=0
Velocity (v) after t seconds, v = gt
Height covered in t seconds, h = ½gt2
Relation between v and u when t is not given: v2 = 2gh
Case 3: When an object is thrown vertically upwards with initial velocity u, the gravitational acceleration will be negative (-g)
Velocity (v) after t seconds, v = u − gt
Height covered in t seconds, h = ut − ½gt2
Relation between v and u when t is gven: v2 = u2 − 2gh
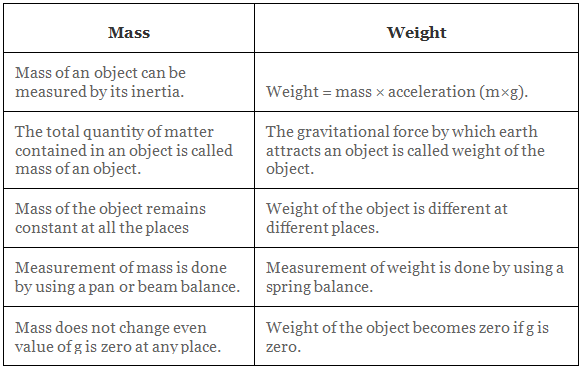
Mass
- The mass of a body is the quantity of matter contained in it. Mass is a scalar quantity which has only magnitude but no direction.
- SI unit of mass is kilogram which is written in short form as kg.
- Mass of a body is constant and does not change from place to place.
- Mass of a body is usually denoted by the small ‘m’.
- Mass of a body cannot be zero.
Weight
- The force with which an object is attracted towards the centre of the earth, is called the weight of the object.
Force = m × a
In case of earth, a = g
∴ F = m× g
But the force of attraction of earth on an object is called its weight (W).
∴ W = m × g - Weight is the force and its SI unit is Newton (N). It depends on ‘g’ and is a vector quantity.
Relation between 1 kg wt and express it into Newton
We know that W = m × g
If mass (m) = 1 kg, g = 9.8 m/s2, then
W = 1 kg × 9.8 m/s2
⇒ 1 kg wt = 9.8 N
- The gravitational force of earth that acts on an object of mass 1 kg is called as 1 kg wt.
Distinguish between Mass and Weight
Factors affecting value of g
- Earth is not a perfect sphere. The radius of earth increases when we go from pole to equator.
- Therefore, we can take g as constant at the surface of earth or closer to it. But, as we move away from earth, we can use equation g = GM/d2 for solving problems.
Example: Calculate the value of ‘g’ at a height of 12800 km from the centre of the earth (radius of earth is 6400 km). Draw its interpretation.
We know that
g1 = (GMe)/(2Re)2
Re = 6400 km
Weight of the object from the centre of earth = 12800 km = 2Re
- The value of gravitational acceleration ‘g’ at a distance of 12800 km from the centre of the earth is ¼.
- The value of gravitational acceleration ‘g’ decreases with increasing height.
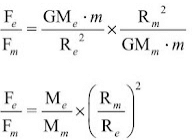
- The weight of an object on moon is one-sixth of the weight on earth.
- Let mass of an object be m, its weight on earth means the force by which earth attracts it towards the centre.
Now, Fe = (GMem)/(Re)2 .... (i)
where,
G = Gravitational constant
Me = Mass of the earth
m = Mass of object
Re = Radius of the earth
- Let mass of an object be m, its weight on earth means the force by which earth attracts it towards the centre.
- Weight of an object on moon(Fm) = (GMmm)/(Rm)2 .... (ii)
where,
Mm = Mass of the moon
Rm = Radius of the moon - Dividing equation (i) by equation (ii), we get
We know that mass of earth is 100 times the mass of the moon.
So, Me = 100 Mm and radius of earth is 4 times the radius of moon.
Re = 4Rm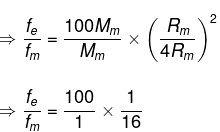
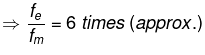
⇒ fe = 6Fm
Thrust and Pressure
- The force acting on an object perpendicular to the surface is called thrust.
- The effect of thrust per unit area is called pressure.
- Pressure (P) = Force/Area = F/A
- SI unit is N/m2 or Nm-2.
- SI unit of pressure is Pascal denoted by ‘Pa’.
- Pressure depends on two factors
(i) Force applied
(ii) Area of surface over which force acts
Examples of Pressure
- The base of high buildings is made wider so that weight of walls act over a large surface area and pressure is less.
- School bags are having broad strap so that the weight of school bags fall over a larger area of the shoulder and produce less pressure and becomes less painful.
- The blades of knives are made sharp so very small surface area and on applying force, it produces large pressure and cuts the object easily.
- All liquids and gases are fluids and they exert pressure in all directions.
Buoyancy
- The upward force experienced by an object when it is immersed into a fluid is called force of buoyancy.
- It acts in upward direction and it depends on the density of the fluid.
- When force of gravitational attraction of the earth on the surface of the object < buoyant force exerted by fluid on the surface of the object, object floats in the fluid.
- When force of gravitational attraction of the earth on the surface of the object > buoyant force exerted by fluid on the surface of the object, the object sinks in the fluid.
- This is the reason, why allpin sinks and boat/ship floats on the surface of water. (Archimedes’ principle)
Density
- The mass per unit volume is called density of an object.
- If M is the mass and V is the volume, then
- Density (d) = Mass(M)/Volume(V)
- SI unit = kg/m3
Archimedes’ Principle
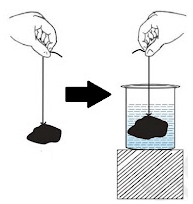
- It states, when a body is immersed fully or partially in a fluid, it experiences a upward force that is equal to the weight of the fluid displaced by it.
Applications of Archimedes’ Principle
- It is used in determining relative density of substances.
- It is used in designing ships and submarines.
- Hydrometers and lactometers are made on this principle.
It is because of this ship made of iron and steel floats in water whereas a small piece of iron sinks in it.
Relative Density
- The ratio of the density of a substance to that of the density of water is called relative density.
- Relative density = Density of a substance/Density of water
- It has no unit as it is a ratio.
Solved Numericals
Example 1: Relative density of gold is 19.3. The density of water is 10 3 kg/m3. What is the density of gold in kg/m3?
Given,
Relative density of gold = 19.3
Density of water = 103 kg/m3
∴ Density of gold = Relative density of gold × Density of water = 19.3 × 103
∵ Density of gold = 19.3 × 103 kg/m3.
Example 2: Mass of 0.025 m 3 of aluminium is 67 kg. Calculate the density of aluminium.
Given,
Mass of aluminium = 67 kg
Volume of aluminium = 0.025 m3
∴ Density = M/V = 67/0.025 = 2680 kg/m3
Example 3: The mass of brick is 2.5 kg and its dimensions are 20 cm×10 cm×5 cm. Find the pressure exerted on the ground when it is placed on the ground with different faces.
Given,
Mass of the brick = 2.5 kg
Dimensions of the brick = 20 cm × 10 cm × 5 cm
∴ Weight of the brick (Thrust/Force)
⇒ F = mg = 2.5 × 9.8 = 24.5 N
- When the surface area 10 cm × 5 cm is in contact with the ground, then
Area = 10 × 5 = 50 cm2
= 50/10000 = 0.005 m2
⇒ P = F/A = 24.5//0.0050 = 4900 N/m2- When the surface area 20 cm×10 cm is in contact with the ground, then
Area = 20 × 10 = 200 cm2
= 20/10000 = 0.02 m2
⇒ P = F/A = 24.5/0.02 = 1225 M/m2
Example 4: A force of 20N acts upon a body whose weight is 9.8N. What is the mass of the body and how much is its acceleration ?
Given,
Force = 20N, Weight W = 9.8N
We know,
W = mg
∴ 9.8 = m × 9.8
⇒ m = 1 kg Ans.
Also,
F = ma
⇒ 20 = 1 × a
⇒ a = 20 m/s2
Example 5: A man weighs 1200N on the earth. What is his mass (take g = 10 m/s2) ? If he was taken to the moon, his weight would be 200N. What is his mass on moon? What is his acceleration due to gravity on moon?
Given,
Weight of man on earth W1 = 1200 N
Weight of man on moon W2 = 200 N
Gravitational acceleration of earth = 10 m/s2
Now,
W = mg
⇒ m = W/g = 120 kg
So, mass on moon will be 120 kg as it is constant everywhere so mass of man on moon = 120 kg.
Now,
W2 = mg2
⇒ 200 = 120 × g2
⇒ g = 200/120 = 10/6 = 5/3 = 1.66 m/s2
Example 6: An object is thrown vertically upwards and reaches a height of 78.4 m. Calculate the velocity at which the object was thrown ? (g = 9.8 m/s2)
Given,
h = 78.4 m
v = 0
g = 9.8 m/s2
Now,
v2 = u2 – 2gh
⇒ u2 – (2×9.8×78.4) = 0
⇒ u2 = 2 × 9.8 × 78.4
Example 7: What is the mass of an object whose weight is 49 Newton?
Given,
Weight of object W = 49N
g = 9.8 m/s2
Now,
W = mg
⇒ m = W/g = 49/9.8 = 5 kg
|
493 videos|387 docs
|
FAQs on Gravitation Summary Class 9 Science Chapter 9
| 1. What is the concept of gravitation in physics? |  |
| 2. What is the role of mass in the gravitational force? |  |
| 3. How does distance affect the gravitational force between two objects? |  |
| 4. How does the concept of gravitational field explain the influence of mass? |  |
| 5. What is the significance of the universal gravitational constant (G) in the concept of gravitation? |  |