NCERT Solutions Class 11 Physics Chapter 11 - Thermodynamics
Q5.1: Choose the correct answer. A thermodynamic state function is a quantity
(i) used to determine heat changes
(ii) whose value is independent of path
(iii) used to determine pressure volume work
(iv) whose value depends on temperature only.
Ans: (ii) whose value is independent of path
Solution: A thermodynamic state function is a quantity whose value is independent of a path.
Functions like P, V, T etc. depend only on the state of a system and not on the path. Hence, alternative (ii) is correct.
Q5.2: For the process to occur under adiabatic conditions, the correct condition is:
(i) ΔT = 0
(ii) Δp = 0
(iii) q = 0
(iv) w = 0
Ans: (iii) q = 0
Solution: A system is said to be under adiabatic conditions if there is no exchange of heat between the system and its surroundings. Hence, under adiabatic conditions, q = 0.
Therefore, alternative (iii) is correct.
Q5.3: The enthalpies of all elements in their standard states are:
(i) unity
(ii) zero
(iii) < 0
(iv) different for each element
Ans: (ii) zero
Solution: The enthalpy of all elements in their standard state is zero.
Therefore, alternative (ii) is correct.
Q5.4: ΔUθ of combustion of methane is -X kJ mol-1 -X . The value of Δ Hθ is
(i) = ΔU θ
(ii) >ΔU θ
(iii) < ΔUθ
(iv) = 0
Ans: (iii) < ΔUθ Q5.5: The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, –890.3 kJ mol–1 –393.5 kJ mol–1, and –285.8 kJ mol–1 respectively. Enthalpy of formation of CH4(g) will be
Q5.5: The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, –890.3 kJ mol–1 –393.5 kJ mol–1, and –285.8 kJ mol–1 respectively. Enthalpy of formation of CH4(g) will be
(i) –74.8 kJ mol–1
(ii) –52.27 kJ mol–1
(iii) +74.8 kJ mol–1
(iv) +52.26 kJ mol–1.
Ans: (i) –74.8 kJ mol–1
Solution: According to the question,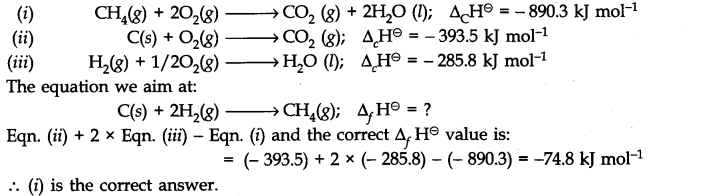 Q5.6: A reaction, A + B → C + D + q is found to have a positive entropy change. The reaction will be
Q5.6: A reaction, A + B → C + D + q is found to have a positive entropy change. The reaction will be
(i) possible at high temperature
(ii) possible only at low temperature
(iii) not possible at any temperature
(iv) possible at any temperature
Ans: (iv) possible at any temperature
Solution: For a reaction to be spontaneous, ΔG should be negative.
ΔG = ΔH – TΔS
According to the question, for the given reaction,
ΔS = positive
ΔH = negative (since heat is evolved)
⇒ ΔG = negative
Therefore, the reaction is spontaneous at any temperature.
Hence, alternative (iv) is correct.
Q5.7: In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy for the process
Ans. According to the first law of thermodynamics,
ΔU = q + W (i)
Where,
ΔU = change in internal energy for a process
q = heat
W = work
Given,
q = + 701 J (Since heat is absorbed)
W = –394 J (Since work is done by the system)
Substituting the values in expression (i), we get
ΔU = 701 J + (–394 J)
ΔU = 307 J
Hence, the change in internal energy for the given process is 307 J.
Q5.8: The reaction of cyanamide, NH2CN(s),with dioxygen was carried out in a bomb calorimeter, and ΔU was found to be –742.7 kJ mol–1at 298 K. Calculate enthalpy change for the reaction at 298 K.
Ans. Enthalpy change for a reaction (ΔH) is given by the expression,
ΔH = ΔU + ΔngRT
Where,
ΔU = change in internal energy
Δng = change in number of moles
For the given reaction,
Δng = ∑ng (products) – ∑ng (reactants)
= (2 – 1.5) moles
Δng = 0.5 moles
And,
ΔU = –742.7 kJ mol–1
T = 298 K
R = 8.314 × 10–3 kJ mol–1 K–1
Substituting the values in the expression of ΔH:
ΔH = (–742.7 kJ mol–1) + (0.5 mol) (298 K) (8.314 × 10–3 kJ mol–1 K–1)
= –742.7 + 1.2
ΔH = –741.5 kJ mol–1
Q5.9: Calculate the number of kJ of heat necessary to raise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 J mol–1 K–1.
Ans: From the expression of heat (q),
q = m. c. ΔT
Where,
c = molar heat capacity
m = mass of substance
ΔT = change in temperature
Substituting the values in the expression of q:
q = (60/27 mol)(24 mol-1 K-1)(20 K)
q = 1066.7 J
q = 1.07 kJ
Q5.10: Calculate the enthalpy change on freezing of 1.0 mol of water at 10.0°C to ice at –10.0°C. ΔfusH = 6.03 kJ mol–1 at 0°C.
Cp[H2O(l)] = 75.3 J mol–1 K–1
Cp[H2O(s)] = 36.8 J mol–1 K–1
Ans: Total enthalpy change involved in the transformation is the sum of the following changes: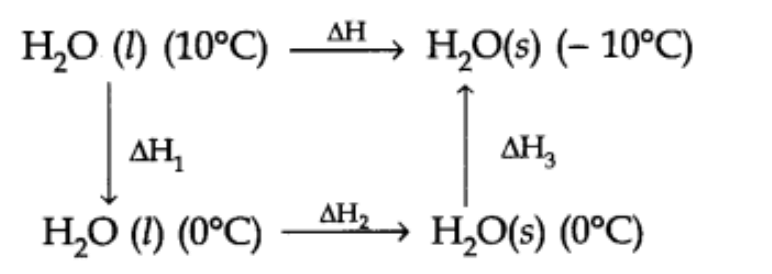 (a) Energy change involved in the transformation of 1 mol of water at 10°C to 1 mol of water at 0°C.
(a) Energy change involved in the transformation of 1 mol of water at 10°C to 1 mol of water at 0°C.
(b) Energy change involved in the transformation of 1 mol of water at 0° to 1 mol of ice at 0°C.
(c) Energy change involved in the transformation of 1 mol of ice at 0°C to 1 mol of ice at –10°C.
Total ΔH = Cp [H2OCl] ΔT + ΔHfreezing + Cp [H2O(s)]ΔT
= (75.3 J mol–1 K–1) (0 – 10)K + (–6.03 × 103 J mol–1) + (36.8 J mol–1 K–1) (–10 – 0)K
= –753 J mol–1 – 6030 J mol–1 – 368 J mol–1
= –7151 J mol–1
= –7.151 kJ mol–1
Hence, the enthalpy change involved in the transformation is –7.151 kJ mol–1.
Note: It is important to note that when any substance transforms from its solid phase to its liquid phase, the change in enthalpy is positive while if the substance is changing its phase from a liquid state to a solid state, then the change in enthalpy is negative. Thus, in this case, the value is considered with a negative sign during the summation of enthalpies.
Q5.11: Enthalpy of combustion of carbon to CO2 is –393.5 kJ mol–1. Calculate the heat released upon formation of 35.2 g of CO2 from carbon and dioxygen gas.
Ans: Formation of CO2 from carbon and dioxygen gas can be represented as:
C(s) + O2(g) → CO2(g) ΔfH = -393.5 kJ mol-1
(1 mole = 44 g)
Heat released on formation of 44 g CO2 = –393.5 kJ mol–1
∴ Heat released on formation of 35.2 g CO2
= (-393.5 kJ mol⁻¹) / (44g) × 35.2 g
= –314.8 kJ mol–1
Q5.12: Enthalpies of formation of CO(g), CO2(g), N2O(g) and N2O4(g) are –110 kJ mol–1, – 393 kJ mol–1, 81 kJ mol–1and 9.7 kJ mol–1 respectively. Find the value of ΔrH for the reaction:
N2O4(g) + 3CO(g)  N2O(g) + 3CO2(g)
N2O(g) + 3CO2(g)
Ans: ΔrH for a reaction is defined as the difference between ΔfH value of products and ΔfH value of reactants.
ΔrH = ∑ΔfH (products) - ∑ΔfH (reactants)
For the given reaction,
N2O4(g) + 3CO(g) → N2O(g) + 3CO2(g)
ΔrH = [{ ΔfH (N2O) + 3ΔfH (CO2) } - { ΔfH (N2O4) + 3ΔfH (CO) }]
Substituting the values of ΔfH for N2O, CO2, N2O4, and CO from the question, we get:
ΔrH = [{81 kJ mol-1 + 3(-393) kJ mol-1} - {9.7 kJmol-1 + 3(-110)kJ mol-1}]
ΔrH = -777.7 kJ mol-1
Hence, the value of ΔrH for the reaction is -777.7 kJ mol-1.
Q5.13: Given
N2(g) + 3H2(g) → 2NH3(g); ΔrHθ = –92.4 kJ mol–1
What is the standard enthalpy of formation of NH3 gas?
Ans: Standard enthalpy of formation of a compound is the change in enthalpy that takes place during the formation of 1 mole of a substance in its standard form from its constituent elements in their standard state.
Re-writing the given equation for 1 mole of NH3(g),
1/2 N₂(g) + 3/2 H₂(g) → NH₃(g)
Therefore, Standard enthalpy of the formation of NH3(g)
= ½ ΔrHθ
= ½ (–92.4 kJ mol–1)
= –46.2 kJ mol–1
Q5.14: Calculate the standard enthalpy of formation of CH3OH(l) from the following data:
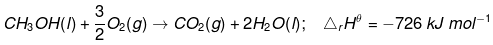
C(g) + O2(g) 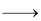 CO2(g) ; ΔcHθ = –393 kJ mol–1
CO2(g) ; ΔcHθ = –393 kJ mol–1
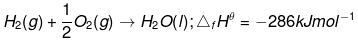
Ans: The reaction that takes place during the formation of CH3OH(l) can be written as:
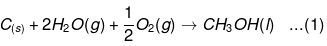
The reaction (1) can be obtained from the given reactions by following the algebraic calculations as:
Equation (ii) + 2 × equation (iii) – equation (i)
ΔfHθ [CH3OH(l)] = ΔcHθ + 2ΔfHθ [H2O(l)] – ΔrHθ
= (–393 kJ mol–1) + 2(–286 kJ mol–1) – (–726 kJ mol–1)
= (–393 – 572 + 726) kJ mol–1
∴ΔfHθ [CH3OH(l)] = –239 kJ mol–1
Q5.15: Calculate the enthalpy change for the process
CCl4(g) → C(g) + 4Cl(g)
and calculate bond enthalpy of C–Cl in CCl4(g).
ΔvapHθ (CCl4) = 30.5 kJ mol–1.
ΔfHθ (CCl4) = –135.5 kJ mol–1.
ΔaHθ (C) = 715.0 kJ mol–1, where ΔaHθ is enthalpy of atomisation
ΔaHθ (Cl2) = 242 kJ mol–1
Ans: The chemical equations implying to the given values of enthalpies are:
(i) CCl4(l) → CCl4(g) ΔvapHθ = 30.5 kJ mol–1
(ii) C(s) → C(g) ΔaHθ = 715.0 kJ mol–1
(iii) Cl2(g) → 2Cl(g) ΔaHθ = 242 kJ mol–1
(iv) C(g) + 4Cl(g) → CCl4(g) ΔfH = –135.5 kJ mol–1
Enthalpy change for the given process CCl4(g) → C(g) + 4Cl(g),can be calculated using the following algebraic calculations as:
Equation (ii) + 2 × Equation (iii) – Equation (i) – Equation (iv)
ΔH = ΔaHθ(C) + 2ΔaHθ (Cl2) – ΔvapHθ – ΔfH
= (715.0 kJ mol–1) + 2(242 kJ mol–1) – (30.5 kJ mol–1) – (–135.5 kJ mol–1)
∴ΔH = 1304 kJ mol–1
Bond enthalpy of C–Cl bond in CCl4 (g)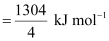
= 326 kJ mol–1
Q5.16: For an isolated system, ΔU = 0, what will be ΔS?
Ans: The change in internal energy (∆U) for an isolated system is zero for it does not exchange any energy with the surroundings. But entropy tends to increase in case of spontaneous reaction. Therefore, ∆S > 0 or positive.
Q5.17: For the reaction at 298 K,
2A + B → C
ΔH = 400 kJ mol–1 and ΔS = 0.2 kJ K–1 mol–1
At what temperature will the reaction become spontaneous considering ΔH and ΔS to be constant over the temperature range?
Ans: From the expression,
ΔG = ΔH – TΔS
Assuming the reaction at equilibrium, ΔT for the reaction would be:
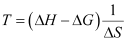
= ΔH/ΔS (ΔG = 0 at equilibrium)
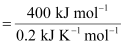
T = 2000 K
For the reaction to be spontaneous, ΔG must be negative. Hence, for the given reaction to be spontaneous, T should be greater than 2000 K.
Q5.18: For the reaction,
2Cl(g) → Cl2(g), what are the signs of ΔH and ΔS ?
Ans: ΔH and ΔS are negative
The given reaction represents the formation of chlorine molecule from chlorine atoms. Here, bond formation is taking place. Therefore, energy is being released. Hence, ΔH is negative.
Also, two moles of atoms have more randomness than one mole of a molecule. Since spontaneity is decreased, ΔS is negative for the given reaction.
Q5.19: For the reaction
2A(g) + B(g) → 2D(g)
ΔUθ = –10.5 kJ and ΔSθ= –44.1 JK–1.
Calculate ΔGθ for the reaction, and predict whether the reaction may occur spontaneously.
Ans: For the given reaction,
2 A(g) + B(g) → 2D(g)
Δng = 2 – (3)
= –1 mole
Substituting the value of ΔUθ in the expression of ΔH:
ΔHθ = ΔUθ + ΔngRT
= (–10.5 kJ) – (–1) (8.314 × 10–3 kJ K–1 mol–1) (298 K)
= –10.5 kJ – 2.48 kJ
ΔHθ = –12.98 kJ
Substituting the values of ΔHθ and ΔSθ in the expression of ΔGθ:
ΔGθ = ΔHθ – TΔSθ
= –12.98 kJ – (298 K) (–44.1 J K–1)
= –12.98 kJ + 13.14 kJ
ΔGθ = + 0.16 kJ
Since ΔGθ for the reaction is positive, the reaction will not occur spontaneously.
Q6.20: The equilibrium constant for a reaction is 10. What will be the value of ΔGθ? R = 8.314 JK–1 mol–1, T = 300 K.
Ans: From the expression,
ΔGθ = –2.303 RT logKeq
ΔGθ for the reaction,
= (2.303) (8.314 JK–1 mol–1) (300 K) log10
= –5744.14 Jmol–1
= –5.744 kJ mol–1
Q6.21: Comment on the thermodynamic stability of NO(g), given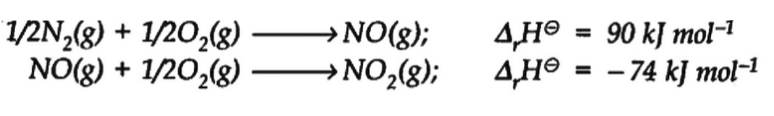 Ans: The positive value of ΔrH indicates that heat is absorbed during the formation of NO(g). This means that NO(g) has higher energy than the reactants (N2 and O2). Hence, NO(g) is unstable.
Ans: The positive value of ΔrH indicates that heat is absorbed during the formation of NO(g). This means that NO(g) has higher energy than the reactants (N2 and O2). Hence, NO(g) is unstable.
The negative value of ΔrH indicates that heat is evolved during the formation of NO2(g) from NO(g) and O2(g). The product, NO2(g) is stabilized with minimum energy.
Hence, unstable NO(g) changes to stable NO2(g).
Q6.22: Calculate the entropy change in surroundings when 1.00 mol of H2O(l) is formed under standard conditions. ΔfHθ = –286 kJ mol–1.
Ans: It is given that 286 kJ mol–1 of heat is evolved in the formation of 1 mol of H2O(l). Thus, an equal amount of heat will be absorbed by the surroundings.
qsurr = +286 kJ mol–1
Entropy change (ΔSsurr) for the surroundings = qsurr/7

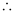 ΔSsurr = 959.73 J mol–1 K–1
ΔSsurr = 959.73 J mol–1 K–1
|
114 videos|263 docs|74 tests
|
FAQs on NCERT Solutions Class 11 Physics Chapter 11 - Thermodynamics
| 1. What is the first law of thermodynamics? |  |
| 2. How is heat different from temperature in thermodynamics? |  |
| 3. What is the significance of the second law of thermodynamics? |  |
| 4. How is work defined in thermodynamics? |  |
| 5. What is the difference between an open, closed, and isolated system in thermodynamics? |  |






















