Vector & Scalar Quantities | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Scalars |

|
| Vectors |

|
| General Points Regarding Vectors |

|
| Scalar or Dot Product of Two Vectors |

|
| Vector or Cross Product of Two Vectors |

|
Different physical quantities can be classified into the following two categories:
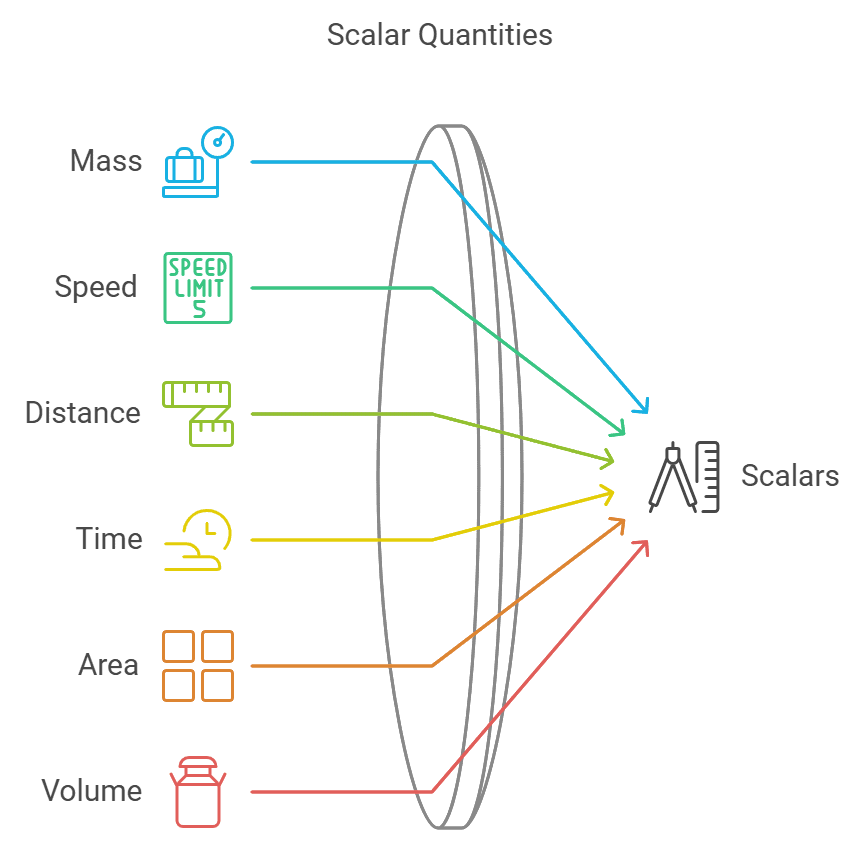
Scalars
Scalar quantity is defined as the physical quantity that has magnitude but no direction.
- It can be represented by a number only. Example: Mass = 4 kg
- The magnitude of mass = 4, Unit of mass = kg
- Scalar quantities can be added, subtracted, and multiplied by simple laws of algebra.
- Examples of Scalar Quantities include mass, speed, distance, time, area, volume, density & temperature.
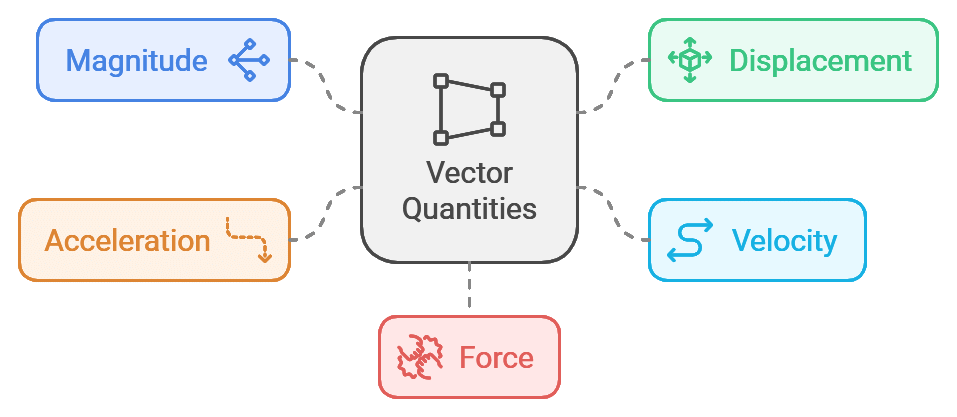
Vectors
A vector quantity is defined as the physical quantity that has both direction as well as magnitude and follows law of vector addition.
 Vectors
Vectors
For example, Speed = 4 m/s (is a scalar), Velocity = 4 m/s toward north (is a vector).
- The magnitude of a vector is the absolute value of a vector and is indicated by |A|.
- Example of Vector quantity: Displacement, velocity, acceleration, force, etc.
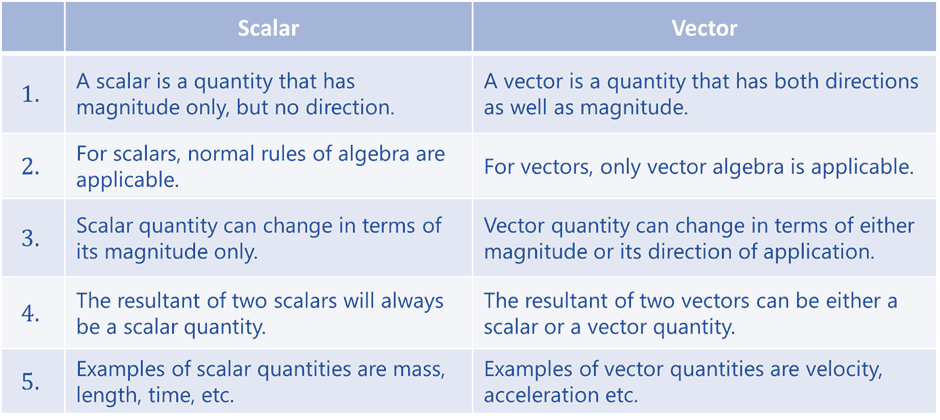
Difference between scalar and vector quantities is mentioned in table below:
Vectors are classified into two types such as :
1. Polar Vectors
Vectors which have a starting point or a point of application are called polar vectors.
Examples are Force, Displacement, etc.
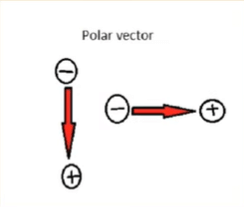 Polar Vectors
Polar Vectors
2. Axial Vectors
Vectors that represent effects of rotation and are directed along the axis of rotation.
Examples of axial vectors include angular velocity, angular momentum, torque, etc.
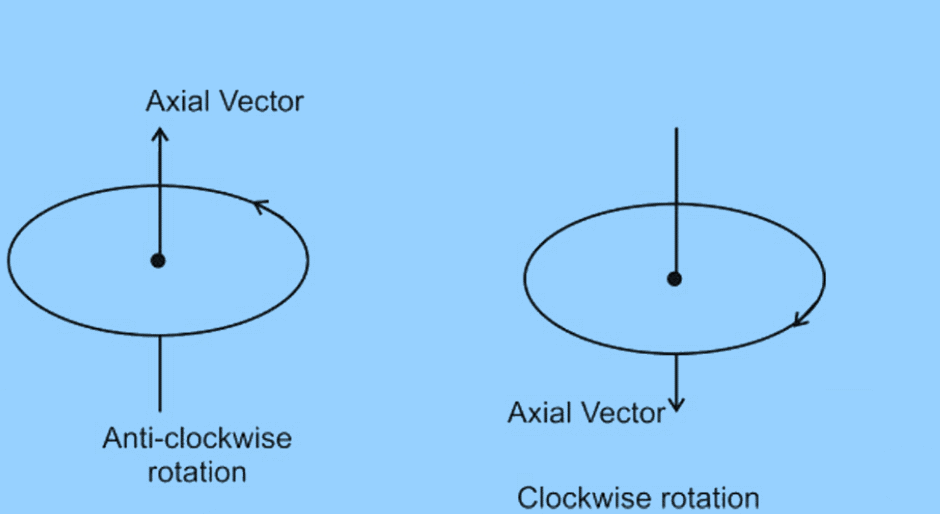 Axial Vectors
Axial Vectors
The direction of an axial vector is determined by the direction of rotation:
- In an anti-clockwise rotation, the axial vector points upwards along the axis of rotation.
- In a clockwise rotation, the axial vector points downwards along the axis of rotation.
- The direction of the axial vector is determined by whether the rotation is anti-clockwise or clockwise.

General Points Regarding Vectors
1. Representation of Vector
- Geometrically, the vector is represented by a line with an arrow indicating the direction of the vector as:
- Mathematically, the vector is represented by
. Sometimes it is represented by the bold letter A.
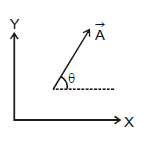
- Thus, the arrow in the above figure represents a vector
in XY-plane making an angle θ with the x-axis.
- Graphical form: A vector is represented by a directed straight line, having the magnitude and direction of the quantity represented by it.
Example: If we want to represent a force of 5 N acting 45° North of East.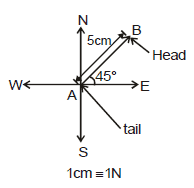
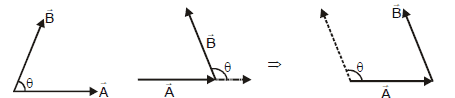
2. The Angle Between Two Vectors (θ)
The angle between two vectors refers to the smaller angle formed between them when they are positioned tail to tail by moving one of the vectors parallel to itself.
3. Unit Vector
A vector having magnitude equal to unity but having a specified direction is called a unit vector.
A unit vector of A is written as 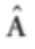 (A cap).
(A cap).
It is expressed as

Q1. 
Sol: 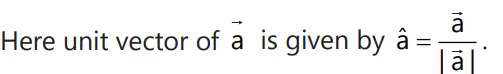
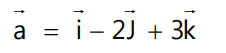
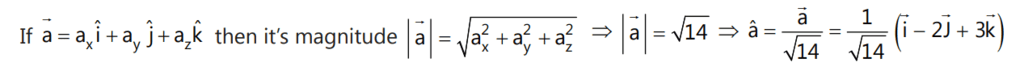
4. Null Vector
A null vector is a vector that has zero magnitude but an undefined or arbitrary direction.
It is also called a zero vector and is represented by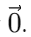 For example, the velocity vector of a stationary object or the acceleration vector of an object moving with uniform velocity are null vectors.
For example, the velocity vector of a stationary object or the acceleration vector of an object moving with uniform velocity are null vectors.
5. Negative of Vector
It implies vectors of the same magnitude but opposite in direction.
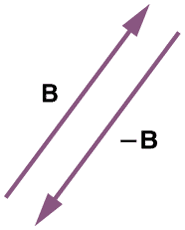 Negative vector
Negative vector
6. Equality of Vectors
Vectors having equal magnitude and same direction are called equal vectors.
7. Collinear Vectors
If any two vectors are collinear, then one can be expressed in terms of the other.
=
(where λ is a constant)
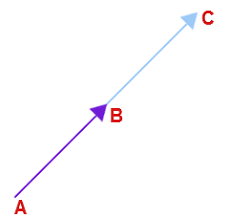 Collinear vector
Collinear vector
8. Co-initial Vector
If two or more vectors start from the same point, then they are called co-initial vectors.
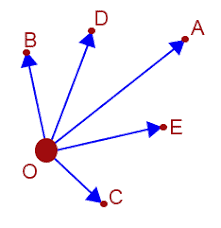
Here A, B, C, D are co-initial vectors.
Q2. 
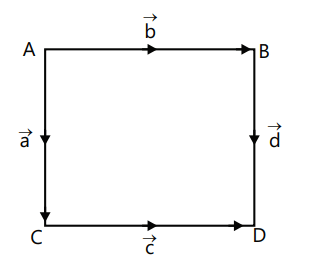
Sol: 
Explanation:

9. Coplanar Vectors
Three (or more) vectors are called coplanar vectors if they lie in the same plane or are parallel to the same plane. Two (free) vectors are always coplanar.
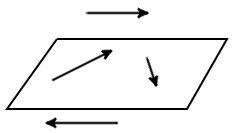 Coplanar VectorsNote: If the frame of reference is translated or rotated the vector does not change (though its components may change).
Coplanar VectorsNote: If the frame of reference is translated or rotated the vector does not change (though its components may change).
10. Orthogonal Unit Vectors
Orthogonal unit vectors are unit vectors that are perpendicular to each other. When two or three unit vectors are at right angles, they are referred to as orthogonal unit vectors.
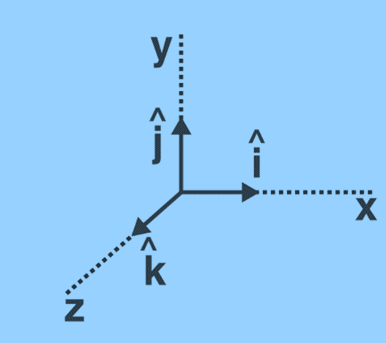 Orthogonal unit vectors
Orthogonal unit vectors

11. Localised Vectors
Localised Vectors are vectors that have a fixed starting point.
For example, consider a vector 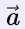 , this vector can be considered as a free vector because it doesn't matter where we draw this vector.
, this vector can be considered as a free vector because it doesn't matter where we draw this vector.
However, the vector 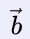 is localised. It has a specific origin (the starting point) and it points towards a certain direction.
is localised. It has a specific origin (the starting point) and it points towards a certain direction.
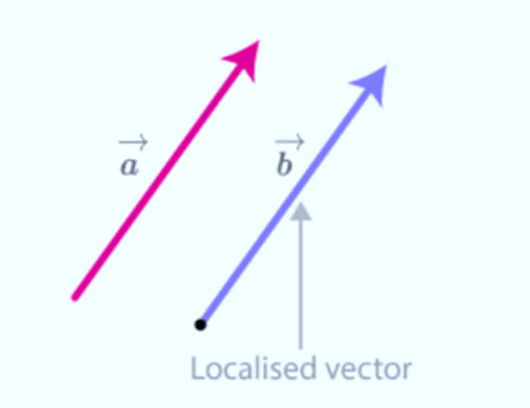 Localised vector
Localised vector
12. Non-localised Vectors
Non-localised Vectors are vectors that do not have a fixed starting point.
For example, the velocity vector of a particle moving along a straight path is considered a non-localised vector. Here, initial point is not fixed.
 Non-localised vector
Non-localised vector
13. Position Vector

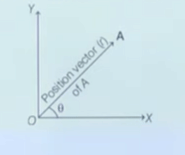
14. Displacement Vector
A displacement vector shows how much and in which direction an object has moved from its initial position to its final position within a certain time.
It is represented by the straight line connecting the starting and ending points, and it does not depend on the actual path taken by the object.


Q3. 
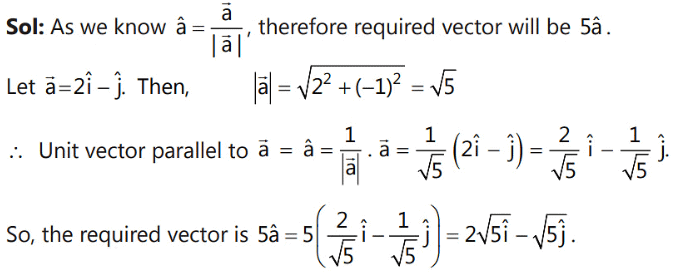
Q4. 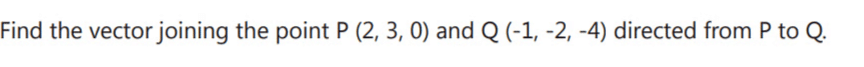

Multiplication of a Vector by a Scalar

Resultant Vector
The resultant vector of two or more vectors is defined as the single vector that has the same effect as all the vectors combined.
There are two main cases:
Case I: When two vectors act in the same direction
- If vectors B are acting in the same direction, the resultant vector R will also be in the same direction as A and B.
- The magnitude of the resultant vector is simply the sum of the magnitudes of A and B, i.e., R=A+B.
Case II: When two vectors act in opposite directions
- If vectors A and B are acting in opposite directions, the resultant vector R will be in the direction of the larger vector.
- The magnitude of the resultant vector will be the absolute difference between the magnitudes of A and R=∣A−B∣.
- If , the direction of R will be along B.
- If , the direction of will be along
Scalar or Dot Product of Two Vectors
The scalar product of two vectors is equal to the product of their magnitudes and the cosine of the smaller angle between them.
It is denoted by .(dot). The scalar or dot product of two vectors is a scalar.
A . B = AB cos θ
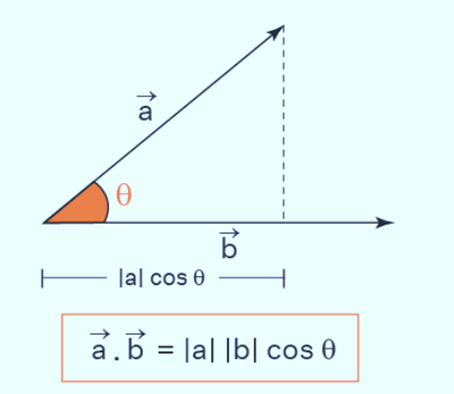
Properties of Scalar Product:
- Scalar product is commutative, i.e.,
A . B= B . A - Scalar product is distributive, i.e.,
A . (B + C) = A . B + A . C - Scalar product of two perpendicular vectors is zero.
A . B = AB cos 90° = 0 - Scalar product of two parallel vectors is equal to the product of their magnitudes, i.e., A . B = AB cos 0° = AB
- Scalar product of a vector with itself is equal to the square of its magnitude, i.e.,
A . A = AA cos 0° = A2 - Scalar product of orthogonal unit vectors is zero and Scalar product in cartesian coordinates is given by AxBx + AyBy + AzBz
Q5. Find the cross product of two vectors a and b if their magnitudes are 5 and 10 respectively. Given that angle between then is 30°.
Sol: 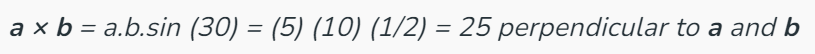
Vector or Cross Product of Two Vectors
The vector product of two vectors is equal to the product of their magnitudes and the sine of the smaller angle between them. It is denoted by X (cross).
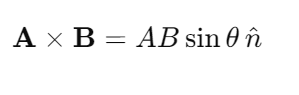
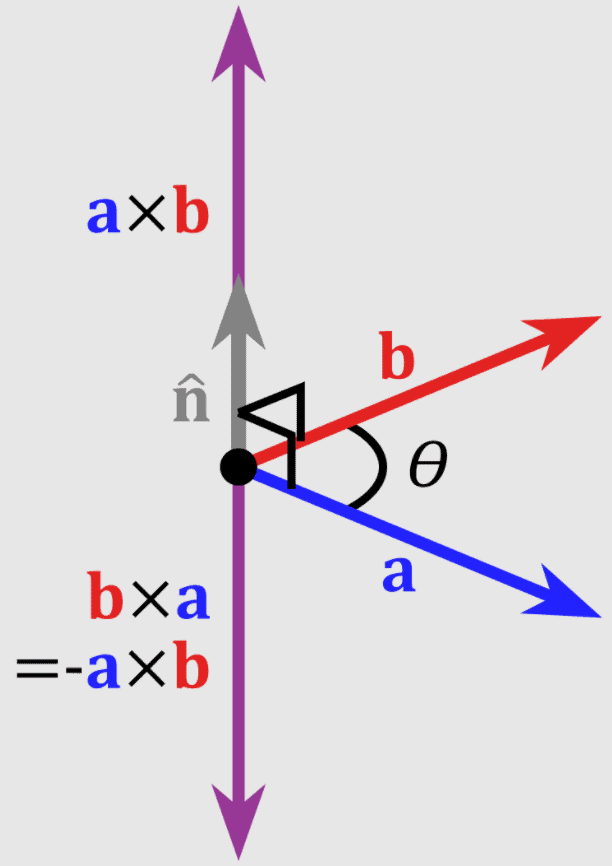 Vector cross product
Vector cross product
- The direction of unit vector n can be obtained from right hand thumb rule.
- If fingers of right hand are curled from A to B through smaller angle between them, then thumb will represent the direction of vector (A X B).
- The vector or cross product of two vectors is also a vector.
Properties of Vector Product:
- Vector product is not commutative, i.e.,
A X B ≠ B X A [ therefore, (A X B) = - (B X A)] - Vector product is distributive, i.e.,
A X (B + C) = A X B + A X C - Vector product of two parallel vectors is zero, i.e.,
A X B = A B sin 0° = 0 - Vector product of any vector with itself is zero.
A X A = A A sin 0° = 0 - On moving in a clockwise direction and taking the cross product of any two pair of the unit vectors we get the third one and in an anticlockwise direction, we get the negative resultant.
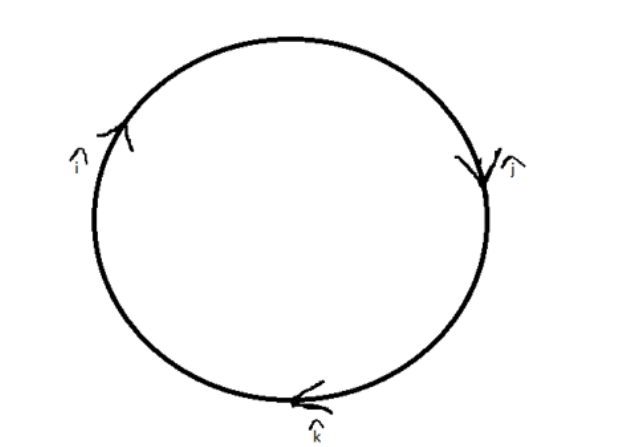
The following results can be established:

Direction of Vector Cross Product
- When C = A X B, the direction of C is at right angles to the plane containing the vectors A and B. The direction is determined by the right hand screw rule, and right hand thumb rule.
- Right Hand Thumb Rule: Curl the fingers of your right hand from A to B. Then, the direction of the erect thumb will point in the direction of A X B.
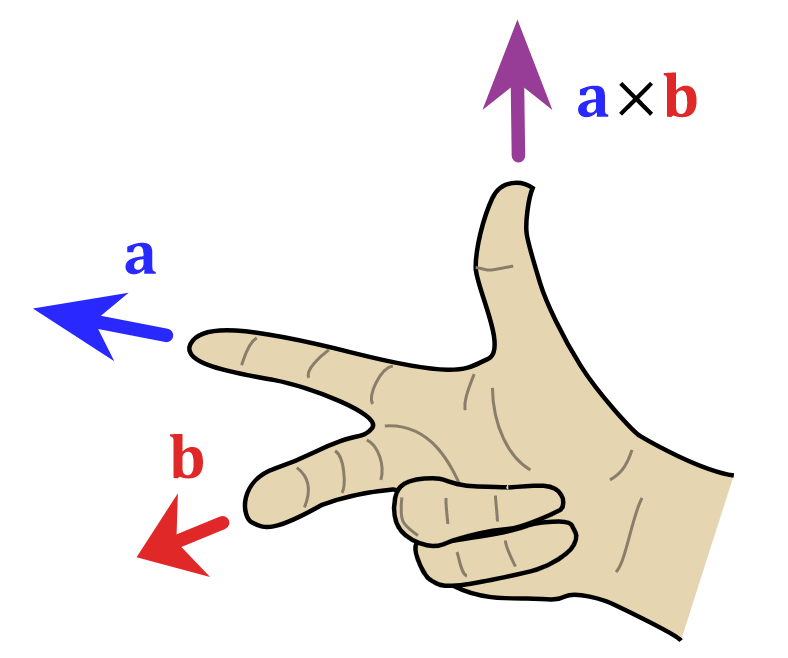 Right Hand Thumb Rule
Right Hand Thumb Rule
- Right Hand Screw Rule: It is also known as Maxwell's Screw Rule, a simple and visual way to determine the direction of a magnetic field or angular motion in relation to a current or rotation.
Explanation: - Imagine holding a screw and turning it with a screwdriver.
- The direction in which you turn the screw (clockwise or counterclockwise) is the direction of rotation.
- The direction in which the screw moves (up or down along the axis) corresponds to the direction of the current or the magnetic field.

Q6. 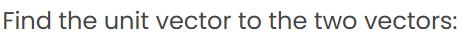
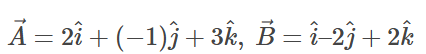
Sol:

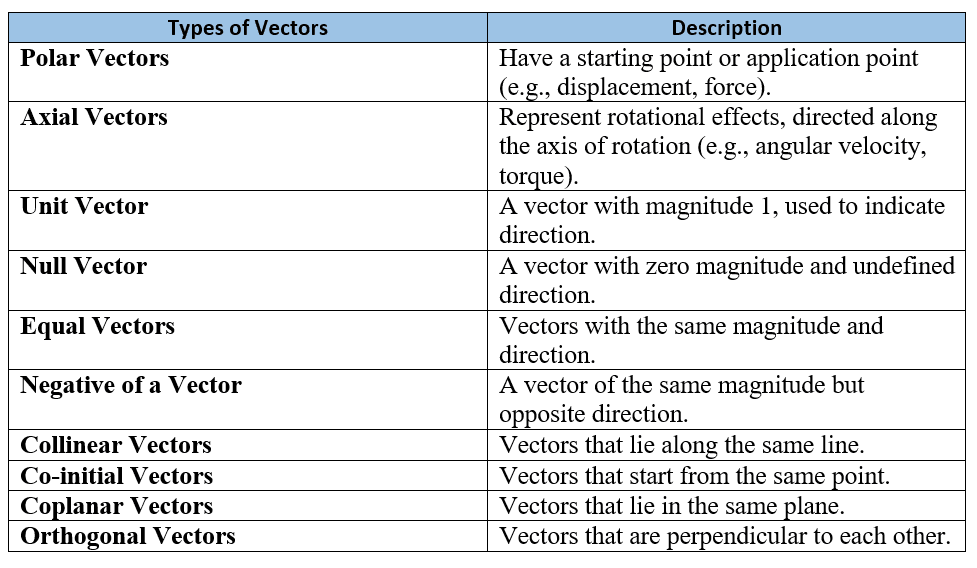
Here is the summarised table of different types of vectors:
|
96 videos|367 docs|98 tests
|
FAQs on Vector & Scalar Quantities - Physics Class 11 - NEET
| 1. What is the difference between scalar and vector quantities? |  |
| 2. How do you calculate the dot product of two vectors? |  |
| 3. What is the significance of the cross product of two vectors? |  |
| 4. Can you give an example of a scalar quantity and a vector quantity? |  |
| 5. What are some common applications of vectors in physics? |  |
















