Previous Year Questions 2025
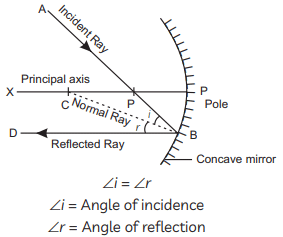
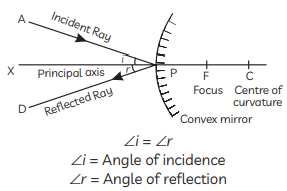
Q1: Mirror 'X' is used to concentrate sunlight in a solar furnace, and Mirror 'Y' is fitted on the side of the vehicle to see the traffic behind the driver. Which of the following statements are true for the two mirrors? (1 Mark)
(i) The image formed by mirror 'X' is real, diminished, and at its focus.
(ii) The image formed by mirror 'Y' is virtual, diminished, and erect.
(iii) The image formed by mirror 'X' is virtual, diminished, and erect.
(iv) The image formed by mirror 'Y' is real, diminished, and at its focus.
(A) (i) and (ii)
(B) (ii) and (iii)
(C) (iii) and (iv)
(D) (i) and (iv)
 View Answer
View Answer 
Ans: (A) (i) and (ii)
- Brief explanation: Mirror X is a concave mirror used to concentrate sunlight — for parallel rays from the Sun it forms a real, highly diminished image at the principal focus. Mirror Y is a convex (rear-view) mirror — it always gives a virtual, diminished, erect image.
Q2: An object is placed at a distance of 60 cm from a concave lens of focal length 30 cm. Use the lens formula to find the position of the image formed in this case. (2 Marks)
 View Answer
View Answer 
Ans:
Use lens formula
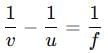
For a concave lens take u =−60 cm (object on left) and f = −30 cm. Substitute:
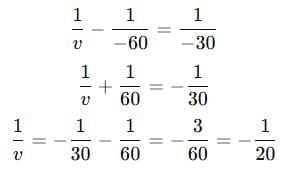
so v = -20 cm
The image is formed at 20 cm on the same side as the object (i.e. v = -20 cm.
Nature: the image is virtual, erect and diminished.
Q3: Draw ray diagrams to show the nature, position, and relative size of the image formed by a convex mirror when the object is placed (i) at infinity and (ii) between infinity and pole P of the mirror. (3 Marks)
 View Answer
View Answer 
Ans:
(i) Object at infinity:
For a convex mirror, when the object is at infinity, incident rays are parallel to the principal axis. After reflection, these rays diverge and appear to come from the focus behind the mirror.
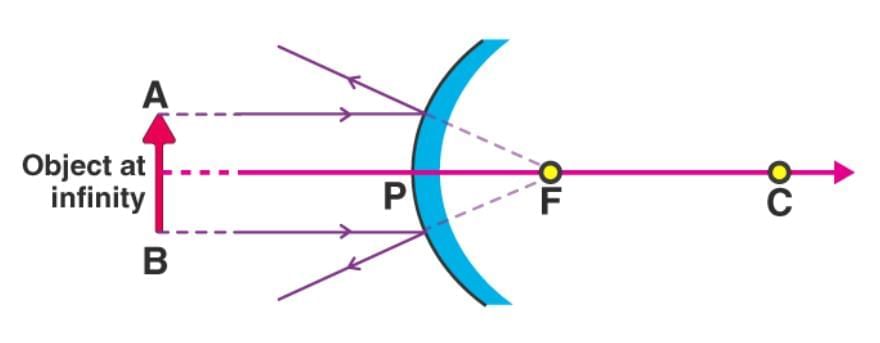
Position: At F (behind the mirror)
Nature: Virtual and erect
Size: Highly diminished (point-like)
(ii) Object between infinity and pole P:
- For any object in front of a convex mirror, the image is always formed between the pole and focus.
Q4: (a) (i) The power of a lens 'X' is -2.5 D. Name the lens and determine its focal length in cm. For which eye defect of vision will an optician prescribe this type of lens as a corrective lens?
(ii) "The value of magnification 'm' for a lens is -2." Using new Cartesian Sign Convention and considering that an object is placed at a distance of 20 cm from the optical centre of this lens, state:
(1) the nature of the image formed;
(2) size of the image compared to the size of the object;
(3) position of the image, and
(4) sign of the height of the image.
(iii) The numerical values of the focal lengths of two lenses A and B are 10 cm and 20 cm respectively. Which one of the two will show a higher degree of convergence/divergence? Give reason to justify your answer. (5 Marks)
OR
(b)
(i) Draw a ray diagram to show the refraction of a ray of light through a rectangular glass slab when it falls obliquely from air into glass.
(ii) State Snell’s law of refraction of light.
(iii) Differentiate between the virtual images formed by a convex lens and a concave lens on the basis of : (I) object distance, and (II) magnification. (5 Marks)
Ans:
(a) (i):
Power P = -2.5 D. From the chapter P = 1/f (with f in metres).
f = 1/P = 1/-2.5 = -0.4 m = -40 cm.
Sign: negative focal length ⇒ concave lens.
Eye defect corrected: Myopia (short-sightedness) — a concave lens diverges incoming rays so the image of distant objects forms at the myopic eye’s far point, enabling clear distant vision.(a) (ii):
Using the new Cartesian sign convention, we take distances measured from the optical centre in the direction of the incident light (from left to right) as positive. Thus, the object placed on the left of the lens is at:u = +20 cmFor a thin lens under this convention, the linear magnification is given bym = v/uso the image distance isv = m·u = (−2) (20 cm) = −40 cm
 View Answer
View Answer 
1. The nature of the image formed:
The negative value of v (i.e. v = −40 cm) indicates that the image is formed on the side opposite to the incident light direction. In this convention, that means the image is real.
The magnification m = −2 is negative, which tells us that the image is inverted relative to the object.
2. Size of the image compared to the size of the object:
The magnitude of the magnification is |m| = 2.
Therefore, the image is twice as large as the object.
3. Position of the Image:
The image is located 40 cm from the optical centre, on the opposite side to the object (to the right of the lens).
4. Sign of the Height of the Image:
Since m = hᵢ / hₒ = −2, if we take the object’s height hₒ as positive (by convention), then the image height hᵢ must be negative. A negative image height indicates that the image is inverted relative to the object.
(a) (iii):
Focal lengths: fA = 10 cm = 0.10 m, fB = 20 cm = 0.20 m.
Power P = 1/f
so
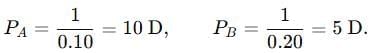
The chapter states a lens with shorter focal length bends rays through larger angles (greater convergence/divergence) and power is the reciprocal of focal length.
So lens A (10 cm) shows the higher degree of convergence/divergence because it has the larger power (10 D vs 5 D).
OR
(b)(i) 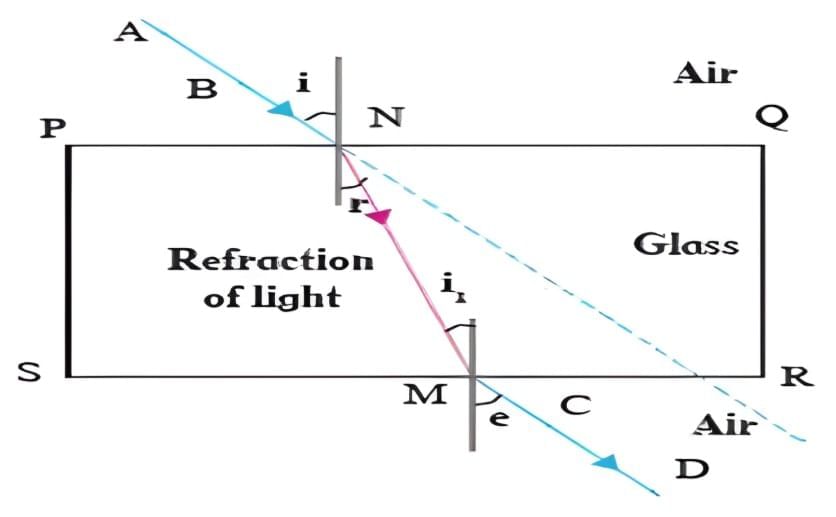
(b) (ii) Snell’s law of refraction
(i) The incident ray, the refracted ray and the normal at the point of incidence all lie in the same plane.
(ii)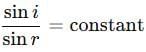 for a given pair of media and light colour. This constant is the refractive index of the second medium with respect to the first (Snell’s law).
for a given pair of media and light colour. This constant is the refractive index of the second medium with respect to the first (Snell’s law).
(b)(iii) Difference between virtual images of a convex lens and a concave lens

Q5: An object is placed at a distance of 30 cm in front of a concave mirror of focal length 20 cm. Use the mirror formula to determine the position of the image formed in this case. (2 Marks)
 View Answer
View Answer 
Ans: The image is formed at 60 cm in front of the mirror
Given:
- Object distance, u = -30 cm (negative due to the new Cartesian sign convention).
- Focal length of concave mirror, f = -20 cm (negative for concave mirror).
- Mirror formula:
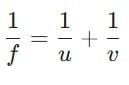
Rearranging for image distance v:
1/v = 1/f - 1/u
Substitute the values:
1/v = 1/(-20) - 1/(-30) = -1/20 + 1/30 = -3/60 + 2/60 = -1/60
v = -60 cm
The negative sign indicates the image is formed in front of the mirror (real image). Thus, the image is at 60 cm in front of the mirror.
Q6: An object is placed at a distance of 10 cm in front of a concave mirror of focal length 15 cm. Use the mirror formula to determine the position of the image formed by this mirror. (2 Marks)
Q7: If the absolute refractive indices of two media X and Y are 6/5 and 4/3 respectively, then the refractive index of Y with respect to X will be: (1 Mark)
(a) 10/9
(b) 9/10
(c) 9/8
(d) 8/9
Q8: An object is placed at a distance of 30 cm from the pole of a concave mirror. If its real and inverted image is formed at 60 cm in front of the mirror, the focal length of the mirror is: (1 Mark)
(a) -15 cm
(b) -20 cm
(c) +20 cm
(d) +15 cm
 View Answer
View Answer 
Ans: (b) -20 cm
Using 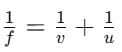
Take u = -30 cm (object to the left) and v = -60 cm (real image in front of mirror, same side as object).
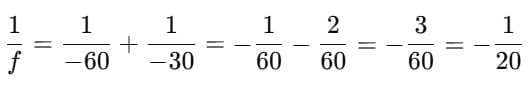
So f = -20 cm.
Q9: A convex lens forms an 8.0 cm long image of a 2.0 cm long object which is kept at a distance of 6.0 cm from the optical centre of the lens. If the object and the image are on the same side of the lens, find (i) the nature of the image, (ii) the position of the image, and (iii) the focal length of the lens. (3 Marks)
 View Answer
View Answer 
Ans:
Given: h = 2.0 cm, h' = 8.0 cm, u = -6.0 cm (object distance taken negative by the New Cartesian sign convention).
Step 1: Magnification: 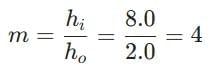
Step 2:
- Object is placed on the same side as the image.- For a convex lens, object distance is usually negative if it is to the left (real object). Here, image is on the same side as object. Since both object and image are on the same side, the image is virtual.
Step 3: Using formula for magnification:
v = −mu
Substitute:
v = −4 × (−6.0) = 24.0 cm
So, the image distance is +24 cm, meaning image is on the opposite side of the lens from the object. This conflicts with the problem statement that both are on the same side.
Since the question says both are on the same side of the lens, and magnification is positive (upright), then for convex lens object is at -6 cm, image should be on the same side (virtual image) with positive magnification.
If we take object distance u=+6 cm (because of sign conventions sometimes vary for virtual object), then and
and
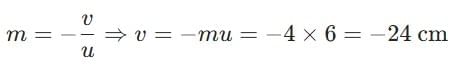 Image distance v =−24 cm indicates image is on the same side as object (virtual image).
Image distance v =−24 cm indicates image is on the same side as object (virtual image).
Step 4:
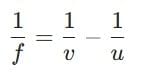
Substitute v=−24 cm and u=6 cm:

Q10: Absolute refractive index of water and glass is 4/3 and 3/2, respectively. If the speed of light in glass is 2 × 10^8 m/s, the speed of light in water is: (1 Mark)
(a) 9/4 m/s
(b) 7/3 m/s
(c) 16/9 m/s
(d) 9/8 m/s
Q11: A convex mirror used for rear view on an automobile has a focal length of 1.5 m. If a 3 m high bus is located at 6.0 m from the mirror, use the mirror formula to determine the position and size of the image of the bus as seen in the mirror. (3 Marks)
 View Answer
View Answer 
Ans: Given: convex mirror, f = +1.5m; object distance u = −6.0m; object height ho = 3m.
Mirror formula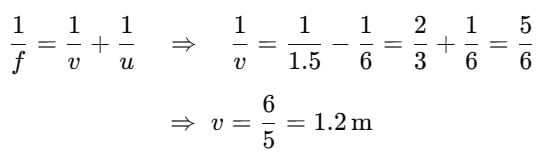
v>0 ⇒ image is behind the mirror (virtual).
Magnification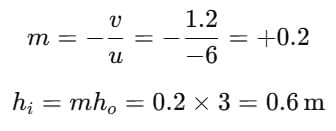
Result: The image is 1.2 m behind the mirror, virtual, erect, and diminished, with height 0.6 m.
Q12: To get an image of magnification -1 on a screen using a lens of focal length 20 cm, the object distance must be: (1 Mark)
(a) Less than 20 cm
(b) 30 cm
(c) 40 cm
(d) 80 cm
 View Answer
View Answer 
Ans: (c) 40 cm
Image on a screen ⇒ real image (thus a convex lens).
For a convex lens, magnification ⇒ v = −u.
Using Lens Formula: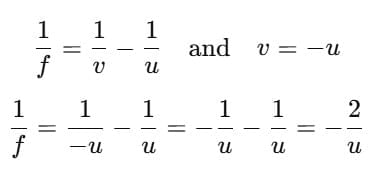
Solve for u: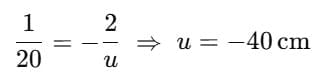 (Sign ‘−’ means the object is placed on the incoming-light side; distance = 40 cm.)
(Sign ‘−’ means the object is placed on the incoming-light side; distance = 40 cm.)
⇒ object is 40 cm from the lens.
Q13: An optical device 'X' is placed obliquely in the path of a narrow parallel beam of light. If the emergent beam gets displaced laterally, the device 'X' is: (1 Mark)
(a) Plane mirror
(b) Convex lens
(c) Glass slab
(d) Glass prism
 View Answer
View Answer 
Ans: (c) Glass slab
When a parallel beam of light passes obliquely through a rectangular glass slab, the emergent ray is parallel to the incident ray but laterally displaced — a characteristic property of a glass slab.
Q14: If we want to obtain a virtual and magnified image of an object by using a concave mirror of focal length 18 cm, where should the object be placed? Use the mirror formula to determine the object distance for an image of magnification +2 produced by this mirror to justify your answer. (3 Marks)
Q15: In order to obtain large images of the teeth of patients, the dentist holds the concave mirror in such a manner that the teeth are positioned: (1 Mark)
(a) at the focus of the mirror
(b) between the pole and the focus of the mirror
(c) between the focus and the centre of curvature of the mirror
(d) at the centre of curvature of the mirror
 View Answer
View Answer 
Ans: (b) between pole and focus of the mirror
When an object is placed between the pole and the focus of a concave mirror, the image formed is virtual, erect, and enlarged, which helps the dentist see a magnified view of the teeth.
Q16: The values of absolute refractive indices of kerosene and water are 1.44 and 1.33, respectively. Compare the two media on the basis of their: (2 Marks)
(a) optical density
(b) mass density
(c) relative speed of propagation of light.
What do you infer on the basis of the above comparisons?
Q17: (A) (a) Observe the following diagram and compare (i) speed of light and (ii) optical density of the three media A, B, and C. Also give justification for your answer of any one of the two cases in terms of refractive indices of A, B, and C.
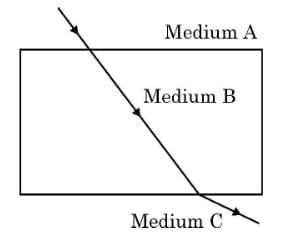 (b) Redraw the path of a ray of light through the three media, if the ray of light starting from medium A falls on the medium B:
(b) Redraw the path of a ray of light through the three media, if the ray of light starting from medium A falls on the medium B:
(i) Obliquely and the optical density of medium B is made more than that of A and C.
(ii) The ray falls normally from medium A to medium B. (5 Marks)
OR
(B) Analyse the following observation table showing variation of image distance (v) with object distance (u) in case of a convex lens and answer the questions that follow without doing any calculations:
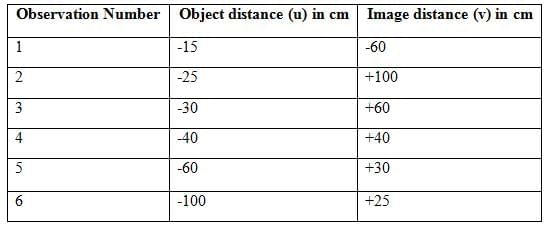
(a) Determine the focal length of the lens. Give reason for your answer.
(b) Find magnification of the image formed in Observation No. 3.
(c) The numerical value of magnifications in cases of observation 1 and 2 is same. List two differences in the images formed in these two cases. (5 Marks)
Ans:
(A)
(a) In this problem, we are comparing the speed of light and optical densities of three media: A, B, and C. The speed of light in a medium is inversely proportional to its optical density. This means that the medium with the highest optical density will have the lowest speed of light.
The refractive index (n) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in the medium (v):
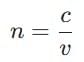
Thus, a higher refractive index indicates a lower speed of light in that medium.
Let’s denote the refractive indices of the three media as follows:
- Refractive index of medium A: 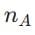
- Refractive index of medium B: 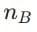
- Refractive index of medium C: 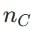
From the problem, if medium B has a higher optical density than A and C, it implies:
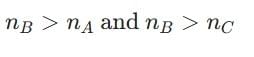 This means that the speed of light in medium B is less than that in A and C:
This means that the speed of light in medium B is less than that in A and C:
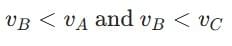
Thus, we can conclude:
Speed of light: Medium B has the lowest speed of light, followed by A, and then C.
Optical densities: Medium B has the highest optical density, followed by A, and then C.
1. Speed of Light Comparison:
- Medium A: vA(higher speed)
- Medium B: vB(lowest speed)
- Medium C: vC (medium speed)
2. Optical Densities Comparison:
- Medium A: lowest optical density
- Medium B: highest optical density
- Medium C: medium optical density
- Speed of Light: 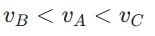
- Optical Densities: 
(b)
(i) When a ray of light travels from medium A to medium B obliquely and medium B has a higher optical density than A, the ray will bend towards the normal upon entering medium B due to the change in speed.
Redraw the path: The ray will enter medium B at an angle less than the angle of incidence in medium A. Let’s denote:
- Angle of incidence in medium A: iA
- Angle of refraction in medium B: rB
Using Snell's law: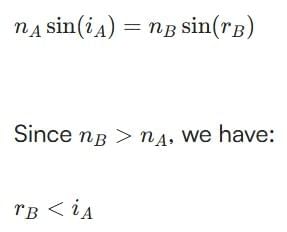
⇒ The ray bends towards the normal when entering medium B obliquely.
(b)
(ii) When the ray of light falls normally from medium A to medium B, it will not bend as the angle of incidence is 0 degrees. The light will continue in a straight line.
Redraw the path: The ray will enter medium B at a right angle (90 degrees) and continue straight without bending.
⇒ The ray continues straight into medium B without bending.
(B)
(a) Focal length: From observation 4, u = -40 cm, v = + 40 cm.
Lens formula: 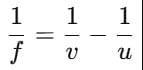
= 1/40 - 1/(-40) = 1/40 + 1/40 = 2/40 = 1/20.f = 20 cm (positive, convex lens).
Reason: The data is consistent with a convex lens of focal length 20 cm, as verified across observations.
(b) Magnification for Observation 3: u = -30 cm, v = +60 cm.
m = v/u = 60/(-30) = -2.
The magnification is -2 (inverted, twice the size).
(c) Differences:
- Observation 1: u = -15 cm, v = -60 cm. m = v/u = -60/(-15) = 4 (positive, virtual, erect image, same side).
- Observation 2: u = -25 cm, v = +100 cm. m = v/u = 100/(-25) = -4 (negative, real, inverted image, opposite side).
Differences:
- Observation 1: Virtual, erect image; Observation 2: Real, inverted image.
- Observation 1: Image on same side as object; Observation 2: Image on opposite side.
Previous Year Questions 2024
Q1: At what distance from a convex lens should an object be placed to get an image of the same size as that of the object on a screen? (2024)
(a) Beyond twice the focal length of the lens.
(b) At the principal focus of the lens.
(c) At twice the focal length of the lens.
(d) Between the optical centre of the lens and its principal focus. View Answer
View Answer 
Ans: (c)
To get an image of the same size as the object using a convex lens, the object should be placed at twice the focal length of the lens. This distance is called "twice the focal length" because at this position, the light rays coming from the object will converge to form an image that is equal in size.
Q2: An object is placed at a distance of 10 cm from a convex mirror of focal length 15 cm. Find the position of the image formed by the mirror. (2024)
 View Answer
View Answer 
Ans:
Given:
- Object distance, (negative, object in front of mirror, Cartesian sign convention).
- Focal length, (positive for convex mirror).
Using the mirror formula:
Substitute:
The image is formed 6 cm behind the convex mirror (positive indicates a virtual image).
Q3: Source-based/case-based questions with 2 to 3 short subparts. Internal choice is provided in one of these sub-parts: (2024)
Study the data given below showing the focal length of three concave mirrors A, B and C and the respective distances of objects placed in front of the mirrors :

(i) In which one of the above cases the mirror will form a diminished image of the object ? Justify your answer.
(ii) List two properties of the image formed in case 2.
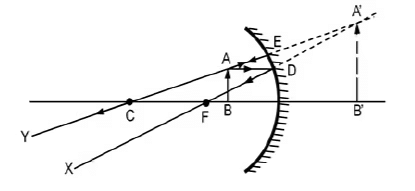
(iii) (A) What is the nature and size of the image formed by mirror C?
Draw ray diagram to justify your answer.
OR
(iii) (B) An object is placed at a distance of 18 cm from the pole of a concave mirror of focal length 12 cm. Find the position of the image formed in this case.
 View Answer
View Answer 
Ans:
i.) Cases:
- Mirror A:
- Mirror B:
- Mirror C:
For a concave mirror, a diminished image is formed when the object is beyond the centre of curvature () or at the centre of curvature ().
- Mirror A: Centre of curvature cm. Since cm, the image is real, inverted, and diminished.
- Mirror B: Centre of curvature cm. Since , the image is real, inverted, and same-sized (considered diminished as it is not magnified).
- Mirror C: cm. The object is between the pole and focus, producing a virtual, erect, and magnified image.
Thus, Mirrors A and B form diminished images.
ii.) For Mirror B: cm.
- The object is at the centre of curvature ( cm).
- Properties:
- Real and inverted: The image forms on the same side as the object and is inverted.
- Same size: The image is the same size as the object, located at the centre of curvature.
OR
(iii) (B) Here ƒ = –12 cm, u = –18 cm, n = ?
Mirror formula:
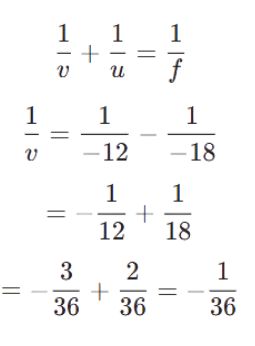 v = -36 cm
v = -36 cm
Q4: (a) State two laws of refraction of light.
OR
(b) Define the term absolute refractive index of a medium. A ray of light enters from vacuum to glass of absolute refractive index 1.5. Find the speed of light in glass. The speed of light in vacuum is 3 x 108 m/s. (2024)
 View Answer
View Answer 
Ans: (a) Laws of Refraction of light :
(i) The incident ray, the refracted ray and the normal to the interface of two transparent media at the point of incidence, all lie in the same plane.
(ii) The ratio of the sine of angle of incidence to the sine of angle of refraction is a constant, for the light of a given colour and for the given pair of media.
OR
(b) Absolute refractive index of a medium is the ratio of speed of light in air/vacuum to the speed of light in the given medium.
Given:
c = 3 × 108 m/s; nm = 1.5; vm = ?
Absolute refractive index of a medium (nm):
nm = speed of light in vacuum (c)speed of light in medium (vm)
nm = cvm
vm = cnm = 2 × 108 m/s
Q5: The Phenomena of light involved in the formation of a rainbow in the sky are (2024)
(a) Refraction, dispersion and reflection
(b) Refraction, dispersion and total internal reflection
(c) Dispersion, scattering and reflection
(d) Dispersion, refraction and internal reflection
 View Answer
View Answer 
Ans: (b)
Refraction:
Light bends when entering a different medium, like when sunlight enters a raindrop.
Dispersion:
Different colors of light bend at slightly different angles within the raindrop, causing them to separate.
Total internal reflection:
Light is trapped inside the raindrop and reflected back out if the angle of incidence is greater than the critical angle.
Q6: Absolute refractive index of glass and water is 3/2 and 4/3 respectively. If the speed of light in glass is 2 x 108 m/s, the speed of light in water is: (2024)
(a) 2.25 × 108 m/s
(b) 52 × 108 m/s
(c) 73 × 108 m/s
(d) 169 × 108 m/s
Q7: (a) The variation of image distance (v) with object distance (u) for a convex lens is given in the following observation table. Analyse it and answer the questions that follow: (2024)
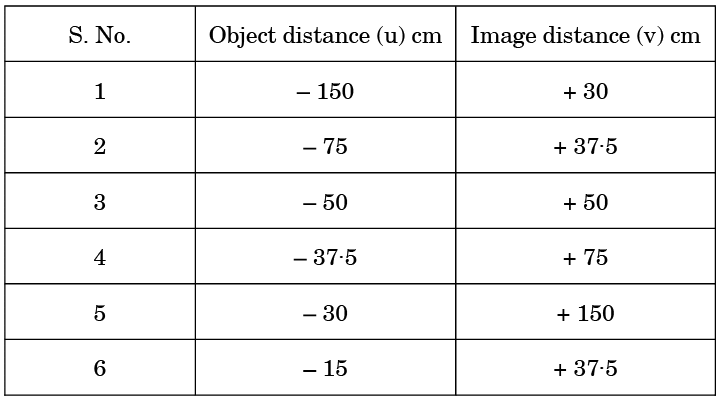
(i) Without calculation, find the focal length of the convex lens. Justify your answer.
(ii) Which observation is not correct ? Why? Draw ray diagram to find the position of the image formed for this position of the object.
(iii) Find the approximate value of magnification for u = - 30 cm.
OR
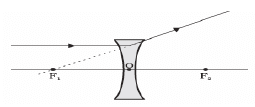
(b) (i) Define principal axis of a lens. Draw a ray diagram to show what happens when a ray of light parallel to the principal axis of a concave lens passes through it.
(ii) The focal length of a concave lens is 20 cm. At what distance from the lens should a 5 cm tall object be placed so that its image is formed at a distance of 15 cm from the lens? Also calculate the size of the image formed.
 View Answer
View Answer 
Ans: (a) (i) S. No. 3, 2f is 50 cm. ∴ 2f = 50 cm, or f = 25 cm.
Justification: Object distance(u) and image distance (v) are same so it implies that object is placed at 2F.
(ii) S. No. 6, is incorrect.
Reason: For u = −15 cm, sign of v must be – ve ( as the image is formed on the same side of the lens as the object)
(iii) Magnification: m = v/u
= +150-30 = - 5 .
OR
(b) (i) Principal axis: It is an imaginary line passing through the two centres of curvatures of a lens.
(ii) f = − 20 cm; h = 5 cm; v = −15 cm
1u = 1v - 1f
or
1u = 1-15 - 1-20
1u = -115 + 120
1u = -460 + 360
1u = -160
u = -60 cm
or u = − 60 cm object is at a distance of 60 cm from the lens
Size of the image(magnification):m = h'h = vu
h' = vu × h = -15-60 × 5 = 1.25 cm
Q8: How will the image formed by a convex lens be affected, if the upper half of the lens is wrapped with black paper? (2024)
(a) The size of the image formed will be one-half of the size of the image due to the complete lens.
(b) The image of the upper half of the object will not be formed.
(c) The brightness of the image will reduce.
(d) The lower half of the inverted image will not be formed.
 View Answer
View Answer 
Ans: (c)
If the upper half of a convex lens is wrapped in black paper, it blocks some light from passing through. As a result, the brightness of the image formed will reduce, but the size and shape of the image will remain the same since the lower half of the lens can still focus the light.
Q9: Case-based/data-based questions with 3 short sub-parts. Internal choice is provided in one of these sub-parts. (2024)
A highly polished surface such as a mirror reflects most of the light falling on it. In our daily life we use two types of mirrors plane and spherical. The reflecting surface of a spherical mirrors may be curved inwards or outwards. In concave mirrors, reflection takes place from the inner surface, while in convex mirrors reflection takes place from the outer surface.
(a) Define the principal axis of a concave mirror.
(b) A ray of light is incident on a concave mirror, parallel to its principal axis. If this ray after reflection from the mirror passes through the principal axis from a point at a distance of 10 cm from the pole of the mirror, find the radius of curvature of the mirror.
(c) (i) An object is placed at a distance of 10 cm from the pole of a convex mirror of focal length 15 cm. Find the position of the image.
OR
(c) (ii) A mirror forms a virtual, erect and diminished image of an object. Identify the type of this mirror. Draw a ray diagram to show the image formation in this case.
 View Answer
View Answer 
Ans: (a) The Principal axis of a concave mirror is an imaginary line that runs through the centre of the mirror, perpendicular to its surface. It is the line along which light rays parallel to it converge after reflection.
(b) Relation between the focal length (f) and the radius of curvature (R):
Given F = 10 cm, therefore R = 20 cm.
Radius of curvature ,R= 20 cm
(c) (i) u = -10 cm, f = +15 cm
1f = 1v + 1u
1v = 1f - 1u = 115 - 1-10
1v = 115 + 110
1v = 16
∴ v = +6 cm
The image is formed at a distance of +6 cm behind the mirror.
OR
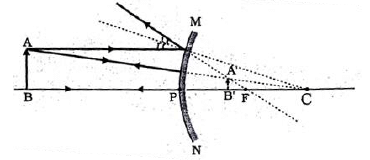
(c) (ii) The mirror that forms a virtual, erect, and diminished image is a convex mirror.
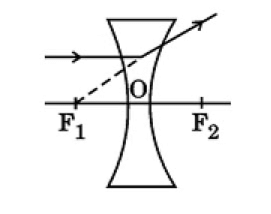
Q10: (a) (i) Draw a ray diagram to show the path of the refracted ray in each of the following cases: (CBSE 2024)
A ray of light incident on a concave lens
(1) parallel to its principal axis, and
(2) is directed towards its principal focus.
(ii) A 4 cm tall object is placed perpendicular to the principal axis of convex lens of focal length 24 cm. The distance of object from the lens is 16 cm. Find the position and size of image formed.
OR
(b) (i) Draw a ray diagram to show the path of the reflected ray in each of the following cases: A ray of light incident on a convex mirror
(1) parallel to its principal axis, and
(2) is directed towards its principal focus
(ii) A 1.5 cm tall candle flame is placed perpendicular to the principal axis of a concave mirror of focal length 12 cm. If the distance of the flame from the pole of the mirror is 18 cm, use mirror formula to determine the position and size of the image formed. (CBSE 2024)
 View Answer
View Answer  Ans: (a) (i)
Ans: (a) (i)
(1) Parallel to its principal axis
 (2) is directed towards its principal focus
(2) is directed towards its principal focus (ii) Given u = –16 cm, f = + 24 cm, h = 4 cm
(ii) Given u = –16 cm, f = + 24 cm, h = 4 cm
Lens formula: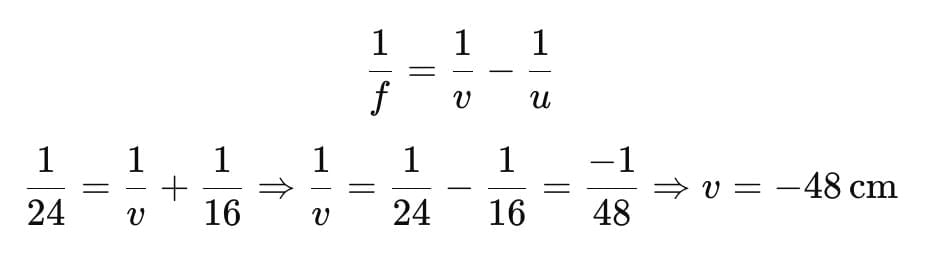
Magnification: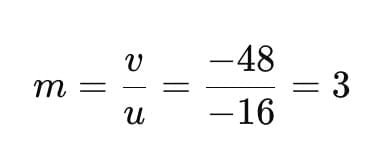
Image height: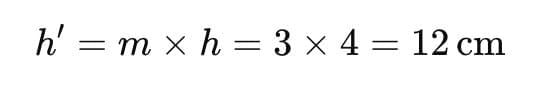
Final Answer:
Position of image: −48cm (on same side as object → virtual and erect)
Size of image: +12cm (3 times taller than the object)
Q11: The color of light for which the refractive index of glass is minimum, is: (CBSE 2024)
(a) Red
(b) Yellow
(c) Green
(d) Violet
 View Answer
View Answer 
Ans: (a)
The refractive index of glass is lowest for red light, meaning that red light travels through glass the fastest compared to other colors. As a result, red light bends the least when it enters the glass, which is why it has the minimum refractive index.
Previous Year Questions 2023
Q1: The magnification produced when an object is placed at a distance of 20 cm from a spherical mirror is +1/2. Where should the object be placed to reduce the magnification to +1/3? (2023)Ans: Initial Setup: View Answer
View Answer 
- Object distance: cm (negative, as the object is in front of the mirror).
- Magnification: (positive, suggesting a virtual, erect image, typical for a convex mirror).
- Magnification formula:
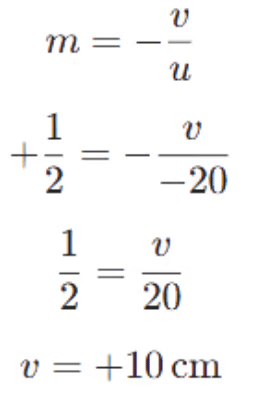 The image is at v=+10cm, virtual and behind the mirror.
The image is at v=+10cm, virtual and behind the mirror.
Find Focal Length:- Use the mirror formula
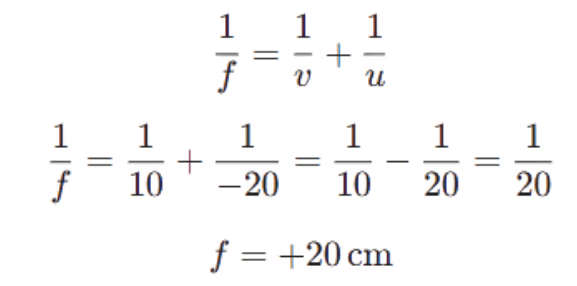 The positive focal length indicates a convex mirror, consistent with the positive magnification.
The positive focal length indicates a convex mirror, consistent with the positive magnification.
Q2: Define the following terms in the context of a diverging mirror: (2023)
(i) Principal focus
(ii) Focal length
Draw a labelled ray diagram to illustrate your answer.
Q3: An object of height 10 cm is placed 25 cm away from the optical centre of a converging lens of focal length 15 cm. Calculate the image distance and height of the image formed. (2023)
Q4: Define power of a lens. The focal length of a lens is -10 cm. Write the nature of the lens and find its power. If an object is placed at a distance of 20 cm from the optical center of this lens, what will be the sign of magnification and nature of image in this case? (2023)
 View Answer
View Answer 
Ans: Power: The ability of a lens to converge or diverge the rays of light is called power of lens. It is the reciprocal of focal length of lens.
P = 1f (cm) = 100f (cm)
Its Sl unit is dioptre.
If f = - 10 cm
P = 100f = -10010 = -10D
So, lens is concave in nature . u = - 20 cm, f = - 10 cm .
As the object placed beyond F image is virtual and thus magnification is +ve.
Q5: The ability of medium to refract light is expressed in terms of its optical density. Optical density has a definite connotation. It is not the same as mass density. On comparing two media, the one with the large refractive index is optically denser medium than the other. The other medium with a lower refractive index is optically rarer. Also the speed of light through a given medium is inversely proportional to its optical density. (2023)
i. Determine the speed of light in diamond if the refractive index of diamond with respect to vacuum is 2.42. Speed of light in vacuum is 3 × 108 m/s.
ii. Refractive indices of glass, water and carbon disulphide are 1.5, 1.33 and 1.62 respectively. If a ray of light is incident in these media at the same angle (say θ), then write the increasing order of the angle of refraction in these media.
iii. (A) The speed of light in glass is 2 × 108 m/s and is water is 2.25 × 108 m/s.
(a) Which one of the two optically denser and why?
(b) A ray of light is incident normally at the water glass interface when it enters a thick glass container filled with water. What will happen to the path of the ray after entering the glass? Give reason.
OR
(B) The absolute refractive indices of glass and water are 4/3 and 3/2, respectively. If the speed of light in glass is 2 × 108 m/s, calculate the speed of light in (i) vacuum (ii) water.
 View Answer
View Answer 
Ans: (i) Refractive index of diamond,
n = Speed of light in vacuumSpeed of light in diamond
n = cv
2.42 = 3 × 108Speed of light in diamond
Speed of light in diamond = 3 × 1082.42
= 1.25 × 108 m/s
(ii) rwater < rglass < rcarbon disulphide
(iii) (A) (a) Since the speed of light is greater in water than in glass, glass is optically denser than water. This demonstrates that glass presents a greater barrier to light transmission than water.
(b) When a ray of light is incident normally at the water-glass interface, it passes straight through without deviation. This happens because the angle of incidence is 0∘, and according to Snell's law, there is no refraction at normal incidence. Only the speed of light decreases in the glass due to its higher refractive index.
OR
(B) Refractive index of glass, ηg = 4/3
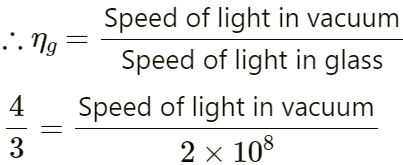
Speed of light in vacuum 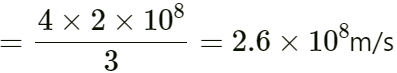
Refractive index of water 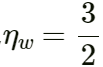
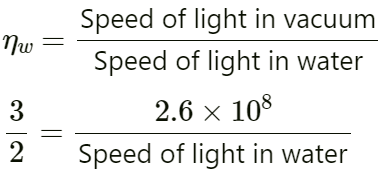
Speed of light in water = 1.73 x 108 m/s
Because the information provided is wrong, ideally the speed of light in vacuum is 3 × 108 m/s and the speed of light in water is 2.25 × 108 m/s.
The correct solution is
Refractive index of glass, ηg = 32
Refractive index of water, ηw = 43
Refractive index of glass, ηg = Speed of light in vacuumSpeed of light in glass
32 = Speed of light in vacuum2 × 108
Speed of light in vacuum = 3 × 2 × 1082 = 3 × 108 m/s
Refractive index of water, ηw = Speed of light in vacuumSpeed of light in water
43 = 3 × 108Speed of light in water
Speed of light in water = 3 × 3 × 1084
Speed of light in water = 2.25 x 108 m/s
Q6: Many optical instruments consists of a number of lenses. They are combined to increase the magnification and sharpness of the image. The net power (P) of the lenses places in contact is given by the algebraic sum of the powers of the individual lenses P1, P2, P3....as
P = P1 + P2 + P3...
This is also termed as the simple additive property of the power of lens, widely used to design lens systems of cameras, microscopes and telescopes. These lens systems can have a combination of convex lenses and also concave lenses. (2023)
(a) What is the nature (convergent/divergent) of the combination of a convex lens of power +4 D and a concave lens of power -2 D?
(b) Calculate the focal length of a lens of power -2.5 D.
(c) Draw a ray diagram to show the nature and position of an image formed by a convex lens of power +0.1 D, when an object is placed at a distance of 20 cm from its optical centre.
OR
(c) How is a virtual image formed by a convex lens different from that formed by a concave lens? Under what conditions do a convex and a concave lens form virtual image?
 View Answer
View Answer 
Ans: (a) Given: P1 = 4 D, P2 = -2 D
P = P1 + P2 = 4D - 2D
So the lens is convergent in nature.
(b) P = -2.5 D
P = 100f (cm) ⇒ −2.5 = 100f (cm) ⇒ f = −40 cm
(c) P = 0.1 D, u = −20 cm
P = 100f (cm) ⇒ 0.1 = 100f ⇒ f = 1000 cm
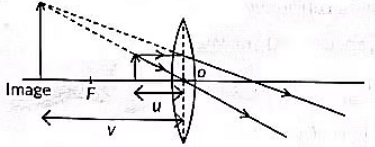
OR
(c) Virtual images formed by convex and concave lenses differ in several ways:
Convex Lens: Forms a virtual image when the object is within the focal length. The image is erect, magnified, and on the same side as the object.
Concave Lens: Always forms a virtual image. The image is erect, diminished, and on the same side as the object.
Q7: Hold a concave mirror in your hand and direct its reflecting surface towards the sun. Direct the light reflected by the mirror on to a white card-board held close to the mirror. Move the card-board back and forth gradually until you find a bright, sharp spot of light on the board. This spot of light is the image of the sun on the sheet of paper; which is also termed as “Principal Focus” of the concave mirror. (CBSE 2023)
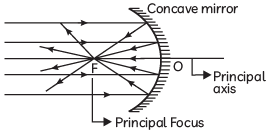
(A) List two applications of concave mirror.
(B) If the distance between the mirror and the principal focus is 15 cm, find the radius of curvature of the mirror.
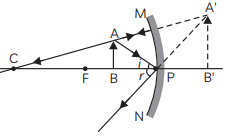
(C) Draw a ray diagram to show the type of image formed when an object is placed between pole and focus of a concave mirror.
(D) An object 10 cm in size is placed at 100 cm in front of a concave mirror. If its image is formed at the same point where the object is located, find:
(i) focal length of the mirror, and
(ii) magnification of the image formed with sign as per Cartesian sign convention.
 View Answer
View Answer 
Ans: (A) Applications of concave mirrors:
(1) Concave mirror is used as a shaving mirror when the face is placed close to it so that it is within its focus and we get an erect and magnified image of the face.
(2) Doctors use concave mirror as a headmirror to concentrate parallel rays of light on its focus which enables them to examine body parts such as eye, throat, etc.
(B) Given, f = 15 cm
We know for a mirror,
R = 2f
R = 2 × 15 cm
R = 30 cm
(C)
(D) (i) We can use the mirror formula to find the focal length of the mirror:
1f = 1v + 1u
where, f is the focal length of the mirror, v is the image distance and u is the object distance. Since the image is formed at the same point as the object, v = u = –100 cm (Distances to the left of the mirror are negative).
Substituting the values, we get:
1f = 1-100 + 1-100
1f = -2100
f = -50 cm
So the focal length of the mirror is –50 cm. (Negative sign indicates that it is a concave mirror).
(ii) The magnification of the image is:
m = - vu
where, m is the magnification of the image.
Substituting the values, we get:
m = - -100-100
m = -1
So the magnification of the image is 1. (Negative sign indicates that the image is real and inverted).
Q8: (A) Complete the following ray diagram to show the formation of image:
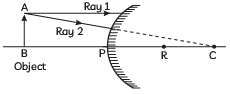
(B) Mention the nature, position and size of the image formed in this case.
(C) State the sign of the image distance in this case using the Cartesian sign convention. (CBSE 2023)
Previous Year Questions 2022
Q1: An optical device forms an erect image of an object placed in front of it. If the size of the image is one half that of the object, the optical device is a (2022)
(a) concave mirror
(b) convex mirror
(c) plane mirror
(d) convex lens.  View Answer
View Answer 
Ans: (b)
Sol: The image formed by a convex mirror is always erect and of smaller in size than object.
Q2: The relation R = 2f is valid (2022)
(a) for concave mirrors but not for convex mirrors
(b) for convex mirrors but not for concave mirrors
(c) neither for concave mirrors nor for convex mirrors
(d) for both concave and convex mirrors.
 View Answer
View Answer 
Ans: (d)
Sol: It is valid for both concave mirrors and convex mirrors.
Q3: In which of the following is a concave mirror used? (2022)
(a) A solar cooker
(b) A rear view mirror in vehicles
(c) A safety mirror in shopping malls
(d) In viewing full size image of distant tall buildings
 View Answer
View Answer 
Ans: (a)
Sol: Concave mirrors are the mirrors best suited ir solar cookers because concave mirrors are convergent mirror and they are reflect sunlight towards a single focal point.
Q4: For the diagram shown, according to the new Cartesian sign convention the magnification of the image formed will have the following specifications : (2022)
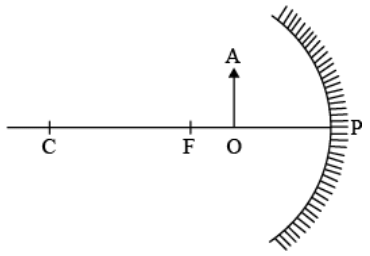
(a) Sign - Positive, Value - Less than 1
(b) Sign - Positive, Value - More than 1
(c) Sign - Negative, Value - Less than 1
(d) Sign - Negative, Value - More than 1
 View Answer
View Answer 
Ans: (b)
Sol: Magnification : Sign-positive, value-more the 1 because the object is placed between the focus and the pole. So, magnified image will be formed on other side of mirror. Hence, magnification of image formed will have i positive sign and value more than one.
Q5: The radius of curvature of a converging mirror is 30 cm. At what distance from the mirror should an object be placed so as to obtain a virtual image? (2022)
(a) Infinity
(b) 30 cm
(c) Between 15 cm and 30 cm
(d) Between 0 cm and 15 cm
 View Answer
View Answer 
Ans: (d)
Radius of curvature of a converging mirror, R = 30 cm
Focal Length, f = 30/2 cm = 15 cm
Thus, virtual image can be obtained from the mirror if an | object is placed between pole and focus, i.e., between 0 i cm and 15 cm.
Q6: Which of the following statements is not true in reference to the diagram shown above? (2022)
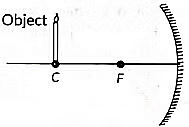 (a) Image formed is real.
(a) Image formed is real.
(b) Image formed is enlarged.
(c) Image is formed at a distance equal to double the focal length.
(d) Image formed is inverted.
 View Answer
View Answer 
Ans: (b)
Sol: Image formed is enlarged is not true. When object is placed at C, image formed is real, inverted and of same size as object.
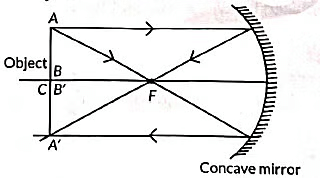
Q7: An object of height 4 cm is kept at a distance of 30 cm from the pole of a diverging mirror. If the focal length of the mirror is 10 cm, the height of the image formed is (2022)
(a) +3.0 cm
(b) +2.5 cm
(c) +1.0 cm
(d) +0.75 cm
 View Answer
View Answer 
Ans: (c)
Sol: Given, height of object (h) = +4 cm
Object distance (u) = -30 cm (object placed left side of the mirror)
Focal length, f = +10 cm
Mirror Formula,
1/f = 1/v + 1/u or v = uf/u - f
v = −30 × 10−30 × 10 or v = 304 = 7.5 cm
Now, Magnification (m) = −vu = h′h ; m = - −152 x 130 x = h′4
or h' = 1 cm
Hence, height of the image formed is 1 cm.
Q8: If a lens and a spherical mirror both have a focal length of -15 cm, then it may be concluded that (2022)
(a) both are concave
(b) the lens is concave and the mirror is convex
(c) the lens is convex and the mirror is concave
(d) both are convex.
 View Answer
View Answer 
Ans: (a)
Sol: As the focal length of a concave mirror and a concave lens is taken as negative, both are concave in nature.
Q9: A student determines the focal length of a device’ A’ by focusing the image of a far off object on a screen placed on the opposite side of the object. The device 'A’ is (2022)
(a) concave lens
(b) concave mirror
(c) convex lens
(d) convex mirror.
 View Answer
View Answer 
Ans: (c)
Sol: If the rays are travelling from far off distance and focused on opposite side of the lens, this is only possible in convex lens.
Q10: When light is incident on a glass slab, the incident ray, refracted ray and the emergent ray are in three media A, B and C. If n1, n2 and n3 are the refractive indices of A, B and C respectively and the emergent ray is parallel to the incident ray, which of the following is true ? (2022)
(a) n1 < n2 < n3
(b) n1 > n2 > n3
(c) n1 < n2 = n3
(d) n1 = n3 < n2
 View Answer
View Answer 
Ans: (d)
Sol: Here, medium A and C is same and 8 is glass. n1 = n3 < n2
Q11: The image of a candle flame formed by a lens is obtained on a screen placed on the other side of the lens. According to new cartesian sign convention, if the image is three times the size of the flame, then the lens is (2022)
(a) concave and magnification is +3
(b) concave and magnification is -3
(c) convex and magnification is -3
(d) convex and magnification is +3.
 View Answer
View Answer 
Ans: (c)
Sol: The image of the candle flame is three times larger than the flame itself, which means the magnification is -3 according to the new Cartesian sign convention, where a negative sign indicates that the image is inverted. Since this type of magnification occurs with a convex lens, the correct answer is that the lens is convex and the magnification is -3.
Q12: The power of a combination of two lenses in contact is +1.0 D. If the focal length of one of the lenses of the combination is +20.0 cm, the focal length of the other lens would be (2022)
(a) -120.0 cm
(b) +80.0 cm
(c) -25.0 cm
(d) -20.0 cm
 View Answer
View Answer 
Ans: (c)
Sol: Given, combined power = +1 D
Focal length of one lens, f1 = 20 cm
Combined focal length, fcombined = 1 m = 100 cm
1f = 1f1 + 1f2 ; 1100 = 120 + 1f2
Solving this equation, we get f2 = -25 cm Focal length of other lens = -25 cm
Q13: Study the diagram given below and identify the type of the lens XX' and the position of the point on the principal axis OO' where the image of the object AB appears to be formed (2022)
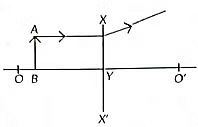
(a) Concave; between O' and Y
(b) Concave : between O and Y
(c) Convex; between O' and Y
(d) Convex; between O and Y
 View Answer
View Answer 
Ans: (b)
Sol: As the ray after passing XX 'is diverging therefore, XX' is concave lens and image is formed between O and Y.
Q14: An object of height 3.0 cm is placed vertically on the principal axis of a convex lens. When the object i distance is -37.5 cm, an image of height -2.0 cm j is formed at a distance of 25.0 cm from the lens. I Next, the same object is placed vertically at 25.0 cm | from the lens. In this situation the image distance v and height h of the image is (according to the new j Cartesian sign convention) (2022)
(a) v = +37.5 cm; h = +4.5 cm
(b) v = -37.5 cm; h = +4.5 cm
(c) v = +37.5 cm; h = - 4.5 cm
(d) v = -37.5 cm; h = -4.5 cm
 View Answer
View Answer 
Ans: (c)
Sol: Given, object height = 3.0 cm
Let object distance is u and image distance is v.
Case-1: u = -37.5 cm and v = 25 cm
h = -2 cm (real and inverted)
From the lens formula, 1f = 1v - 1u = 125 - 1-37.5
f = +15 cm ... (i)
Case2: u = -25 cm, f = +15 cm (from (i))
By lens formula:
1f = 1v - 1u
115 = 1v - 125
v = +37.5 cm
Now, h1 = 3 cm and h = ?
Magnification:
m = vu = hh1
∴ +37.5-25 = h+3
∴ h = -4.5 cm
Q15: An object is placed in front of a concave lens. For all positions of the object the image formed is always (2022)
(a) Real, diminished and inverted
(b) Virtual, diminished and erect
(c) Real, enlarged and erect
(d) Virtual, erect and enlarged.
 View Answer
View Answer 
Ans: (b)
Sol: The image formed by of a concave lens is always virtual, diminished and erect.
Q16: A ray of light starting from air passes through a medium A of refractive index 1.50, enters medium B of refractive index 1.33 and finally enters medium C of refractive index 2.42. If this ray emerges out in air from C, then for which of the following pairs of media the bending of light is least? (2022)
(a) air-A
(b) A-B
(c) B-C
(d) C-air
 View Answer
View Answer 
Ans: (b)
Sol: As refractive index of a medium increases, more bending of light takes place. For A - B, ratio of refractive indices of A and B is least, so least bending of light takes place for this pair of media.

Q17: A ray of light is incident as shown. If A, B and C are three different transparent media, then which among the following options is true for the given diagram? (2022)
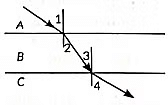
(a) ∠1 > ∠4
(b) ∠1< ∠2
(c) ∠3 = ∠2
(d) ∠3 > ∠4
 View Answer
View Answer 
Ans: (c)
Sol: In A, B and C transparent media, ∠1 > ∠2 as light bends towards the normal and ∠3 < ∠4 as light bends away from the normal. ∠3 = ∠2 , because of alternate angles between two normals.
Q18: In the diagram shown above n1, n2 and n3 are refractive indices of the media 1, 2 and 3 respectively. Which one of the following is true in this case. (2022)
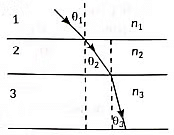
(a) n1 = n2
(b) n1 > n2
(c) n2 > n3
(d) n3 > n1
 View Answer
View Answer 
Ans: (d)
Sol:
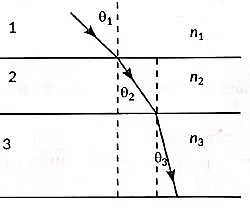
In medium 2, the light ray bends towards the normal, so n2 > n1.
Similarly, in medium 3, the light ray bends more towards the normal which indicate that refractive index of medium 3 is greater than medium 2. So, n3 > n1
Q19: The refractive index of medium A is 1.5 and that of medium B is 1.33. If the speed of light in air is 3 x 108 m/s, what is the speed of light in medium A and B respectively? (2022)
(a) 2 x 108 m/s and 1.33 x 1 08 m/s
(b) 1.33 x 108 m/s and 2 x 108 m/s
(c) 2.25 x 108 m/s and 2 x 108 m/s
(d) 2 x 108 m/s and 2.25 x 108 m/s
 View Answer
View Answer 
Ans: (d)
Sol: Given, refractive index of medium A, μA = 1.5
Refractive index of medium B, μB = 1.33
Speed of light in air, c = 3 x 108 m/s
μ = Speed of light in vacuum (c)Speed of light in medium (v)
For medium A:
μA = cvA ⇒ 1.5 = 3 × 108vA m/s
vA = 2 × 108 m/s
For medium B:
μB = cvB ⇒ 1.33 = 3 × 108vB m/s
VB = 2.25 x 108 m/s
Hence, speed of light in medium A is 2 x 108 m/s and in medium B is 2.25 x 108 m/s.
Q20: A student wants to obtain magnified image of an object AB as on a Screen. Which one of the following arrangements shows the correct position of AB for him/her to be successful? (2022)
(a) 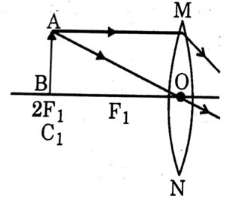
(b) 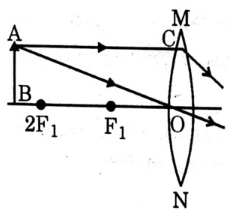
(c) 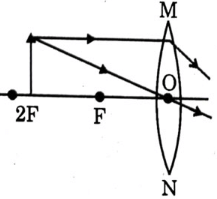
(d) 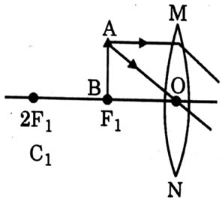
 View Answer
View Answer 
Ans: (c)
Sol: To get real & magnified image, object should be kept either between 2F and F or at F. If it is kept at F, image will form at infinity which cannot be taken on screen, so object should be kept between 2F and F.
Q21: The following diagram shows the use of an optical device to perform an experiment of light. As per the arrangement shown, the optical device is likely to be a (2022)
(a) concave mirror
(b) concave lens
(c) convex mirror
(d) convex lens
 View Answer
View Answer 
Ans: (b)
Sol: As per the arrangement, an optical device to perform an experiment of light is likely to be a concave lens.
Q22: If a lens can converge the sun rays at a point 20 cm j away from its optical centre, the power of this lens is (2022)
(a) +2D
(b) -2D
(c) +5D
(d) -5D
 View Answer
View Answer 
Ans: (c)
Sol: Converging point, f = 20 cm
Power P = ?
As we know that,
Power of lens = 1focal length (in m) = 1f (in m)
P = 10020 ⇒ P = +5 D
Hence, power of convex lens is +5 D.
Q23: A converging lens forms a three-times magnified image of an object, which can be taken on a screen. If the focal length of the lens is 30 cm, then the distance of the object from the lens is (2022)
(a) -55 cm
(b) -50 cm
(c) -45 cm
(d) -40 cm
 View Answer
View Answer 
Ans: (d)
Sol: –40 cm
Reason — Given, convex lens as converging lens
f = 30 cm
From formula,
m = v/u
-3 = v/u [-ve sign as real and inverted image is formed.]
v = -3u
Using formula,
1/f = 1/v - 1/u
We get,
130 = 1-3u - 1u
130 = -1 - 33u = -43u
3u = -4 × 30
u = -1203 = -40 cm
Hence, distance of the object from the lens = -40 cm.
Previous Year Questions 2021
Q1: The refractive index of glass is 1.50. What is the meaning of this statement? (2021) View Answer
View Answer 
Ans: It gives us the idea about the speed of light in the air and in the glass. It means that speed of light is 1.5 time more in air than the speed of light in the glass.
Q2: A ray of light starting from air passes through medium A of refractive index 1.50, enters medium B of refractive index 1.33 and finally enters medium C of refractive index 2.42. If this ray emerges out in air from C, then for which of the following pairs of media the bending of light is least?
(a) air-A
(b) A-B
(c) B-C
(d) C-air (CBSE Term-1 2021)
 View Answer
View Answer 
Ans: (b)
The bending of light depends on the difference in refractive indices between two media. The smaller the difference in refractive indices, the less the light will bend when passing from one medium to another.
For each pair of media:
- Air-A: The difference in refractive indices is |1.00 - 1.50| = 0.50.
- A-B: The difference in refractive indices is |1.50 - 1.33| = 0.17.
- B-C: The difference in refractive indices is |1.33 - 2.42| = 1.09.
- C-Air: The difference in refractive indices is |2.42 - 1.00| = 1.42.
The smallest difference is between A and B, which has a refractive index difference of 0.17. Therefore, the bending of light will be least when it passes between A and B.
Thus, the correct answer is (b) A-B.
Q3: A converging lens forms three times magnified image of an object, which can be taken on a screen. If the focal length of the lens is 30 cm, then the distance of the object from the lens is:
(a) –55 cm
(b) –50 cm
(c) –45 cm
(d) –40 cm (CBSE Term-1 2021)
 View Answer
View Answer 
Ans: (d)
Given:
The lens forms a real, three times magnified image (m = -3 because the image is real and inverted).
Focal length f = 30cm.
For a lens, the magnification m is given by: m = vu
where v is the image distance and u is the object distance. Since m = −3:
vu = -3 ⇒ v = -3u
Using the lens formula:
1f = 1v - 1u
Substitute f = 30cm and v = −3u:
130 = 1-3u - 1u
Simplify this equation:
130 = -1 - 33u = -43u
Now, solve for u:
u = -4 × 303 = -40 cm
Therefore, the distance of the object from the lens is –40 cm.
Q4: An object of height 4 cm is kept at a distance of 30 cm from the pole of a diverging mirror. If the focal length of the mirror is 10 cm, the height of the image formed is:
(a) +3.0 cm
(b) +2.5 cm
(c) +1.0 cm
(d) +0.75 cm (CBSE Term-1 2021)
 View Answer
View Answer 
Ans: (c)
Given:
Height of the object, h = 4cm
Object distance from the mirror, u = −30cm (distance is negative for mirrors according to the sign convention)
Focal length of the diverging (concave) mirror, f = −10cm
We need to find the height of the image h′.
1f = 1v + 1u
Substitute the given values into the formula:
1-10 = 1v + 1-30
Simplify the equation:
1v = -330 + 130 = -230 = -115
Therefore:
v = -15 cm
Calculating the magnification (m):
m = hiho = vu
Substitute the known values:
m = -15-30 = 12
Also, To find the height the value of hi
Using the magnification formula:
m = hiho
Substitute the values of m and ho:
12 = hi4
Solve for hi:
hi = 12 × 4 = 2 cm
So, the height of the image formed is 2 cm.
Previous Year Questions 2020
Q1: Define pole of a spherical mirror. (2020)
 View Answer
View Answer 
Ans: The pole of a spherical mirror define the geometrical center of the spherical surface of the mirror. It is the center of reflecting surface of spherical mirror and lies on the surface of spherical mirror.
Q2: The refractive index of a medium 'x' with respect to a medium 'y' is 2/3 and the refractive index of medium 'y' with respect to medium 'z' is 4/3. Find the refractive index of medium 'z' with respect to medium 'x'. If the speed of light in medium 'x' is 3 x 108 m s-1, calculate the speed of light in medium 'y. (2020)
 View Answer
View Answer 
Ans: Given, refractive index of medium x with respect to y, vμx = 23
Refractive index of medium y with respect to z, zμy = 43
∴ Refractive index of medium x with respect to z, zμx = vμx x zμy = 23 × 43 = 89
∴ Refractive index of medium z with respect to x, xμz = 1zμz = 98
Now, speed of light in x = 3 × 108 m/s
Speed of light in y, vy = ?
yμx = Speed of light in xSpeed of light in y
⇒ vy = 23 × 3 × 108 = 2 × 108 m/s
Q3: Study the ray diagram given below and answer the questions that follow: (2020)
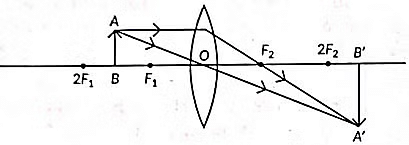 (a) Is the type of lens used converging or diverging?
(a) Is the type of lens used converging or diverging?
(b) List three characteristics of the image formed.
(c) In which position of the object will the magnification be - 1?
 View Answer
View Answer 
Ans: (a) We have used a converging lens.
(b) The characteristics of the image formed:
(i) It is real.
(ii) It is inverted
(iii) It is enlarged.
(c) We get the magnification of object, m = - 1 at the position 2F1.
Q4: Rishi went to a palmist to show his palm. The palmist used a special lens for this purpose. (2020)
(i) State the nature of the lens and reason for its use.
(ii) Where should the palmist place/hold the lens so as to have a real and magnified image of an object?
(iii) If the focal length of this lens is 10 cm, the lens is held at a distance of 5 cm from the palm, use lens formula to find the position and size of the image. (2020)
 View Answer
View Answer 
Ans: (i) The lens used here is a convex lens and it is used as a magnifying glass because at close range, i.e., when the object is placed between optical centre and principal focus it forms an enlarged, virtual and erect image of the object.
(ii) When this lens is placed such that the object is between the centre of curvature and the principal focus, the palmist obtain a real and magnified image.
(iii) Given, focal length, f = 10 cm and u = -5 cm
According to lens formula,
1f = 1v − 1u or 1f = 1u + 1v
= 110 + 1−5 = −5 + 10−50
∴ v = −505 = −10 cm
Thus, the image will be formed at 10 cm on the same side of the palm and the size of the image will be enlarged.
Q5: Draw ray diagram in each of the following cases to show what happens after reflection to the incident ray when:
(A) it is parallel to the principal axis and falling on a convex mirror.
(B) it is falling on a concave mirror while passing through its principal focus.
(C) it is coming oblique to the principal axis and falling on the pole of a convex mirror. (CBSE 2020)
 View Answer
View Answer 
Ans: (A) An incident ray parallel to the principal axis, after reflection appear to diverge from the principal focus, in the case of a convex mirror
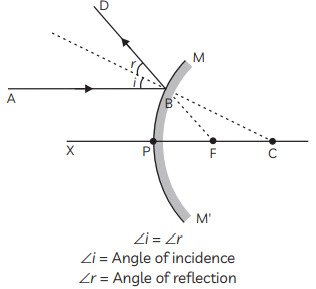
A straight line XP is principal axis. AB is incident ray which is parallel to principal axis XP of a convex mirror MM’. The ray of light gets reflected at point B on the mirror and goes in the direction BD and it appears to be coming from the focus F of convex mirror. According to the laws of reflection, ∠i = ∠r. Therefore, the incident and reflected rays make equal angles with the normal.
(B) An incident ray passing through the principal focus of a concave mirror, after reflection, will emerge parallel to the principal axis
(C) An incident ray coming obliquely to the principal axis towards a point (Pole of the mirror) on the convex mirror is reflected obliquely.
Q6: (A) A person suffering from myopia (nearsightedness) was advised to wear corrective lens of power – 2.5 D. A spherical lens of same focal length was taken in the laboratory. At what distance should a student place an object from this lens so that it forms an image at a distance of 10 cm from the lens?
(B) Draw a ray diagram to show the position and nature of the image formed in the above case. (CBSE 2020)
 View Answer
View Answer 
Ans: (A)
P = −2.5 D
f = ?
P = 1f
f = 1P = 1−2.5 D
f = −0.4 m = −40 cm
f = −40 cm
v = −10 cm
u = ?
1f = 1v − 1u
1u = 1v − 1f
1u = 1−10 − 1−40
= −110 + 140 = −4 + 140
= −340
u = −403 cm
= -13.33 cm
The object should be placed – 13.33 cm from the lens for the formation of an image at a distance of 10 cm from the lens.
(B)
Q7: Draw a ray diagram in each of the following cases to show the formation of image, when the object is placed:
(A) between optical centre and principal focus of a convex lens.
(B) anywhere in front of a concave lens.
(C) at 2F of a convex lens.
State the signs and values of magnifications in the above mentioned cases (A) and (B). (CBSE 2020)
 View Answer
View Answer 
Ans: (A) When an object is placed in front of the lens between optical centre and principal focus of a convex lens, the image is formed beyond 2F1 (on the same side of the object).
AB is the object and A’B’ is the image. The image formed is enlarged, virtual and erect. So the value of magnification will be greater than 1 and its sign will be positive.
(B) When an object a placed anywhere infront of a concave lens. When we place an object between infinity and optical centre (O) of the concave lens, the image will be formed between focus (F1) and optical centre (O) on the same side of the lens.
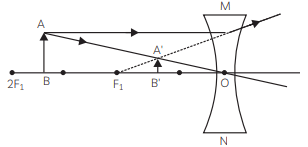
AB is the object and A’B’ is the image. The image formed is diminished, virtual and erect. So the sign of magnification is positive (+) and the magnification will be less than 1.
(C) When the object is placed at 2F1 of convex lens, the image is formed at 2F2 on the other side of the lens.
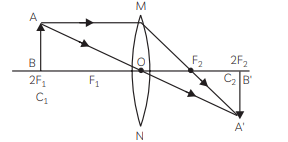 The image formed is real, inverted and of the same size.
The image formed is real, inverted and of the same size.
Previous Year Questions 2019
Q1: How far should an object be placed from a convex lens of focal length 20 cm to obtain its real image at a distance of 30 cm from the lens? Determine the height of the image if the object is 4 cm tall. (2019) View Answer
View Answer 
Ans: Focal length of convex lens (f) = 20 cm
Real image formed at a distance, (v) = 30 cm
Height of image (h1) = 4 cm
Let the object distance be u.
Lens formula,
1v − 1u = 1f ⇒ 130 − 1u = 120
u = −60 cm
From,
m = vu = 30−60 = −12
m = h'h = −12
h' = −12 × 4
h' = −2 cm
Hence, height of image of object is -2 cm.
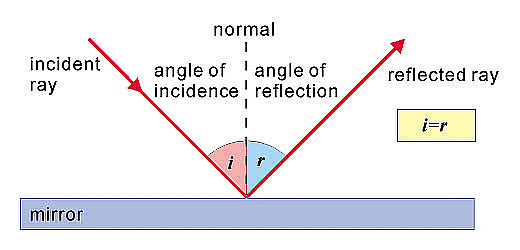
Q2: State laws of reflection of light. List four characteristics of the image formed by a plane mirror. (2019)
 View Answer
View Answer 
Ans: The laws of reflection of light state that:
- The incident ray, the reflected ray and the normal to the surface at the point of incidence all lie in the same plane.
- The angle of incidence (i) is always equal to the angle of reflection (∠r) i.e. ∠i = ∠r
Characteristics of the image formed by a plane mirror
- Image formed in a plane mirror is virtual and erect.
- It is the same size as the object.
- The image formed is laterally inverted.
- The image formed is at same distance behind the mirror as object is in front of mirror.
Q3: A student, holding a mirror in his hand, directed the reflecting surface of the mirror towards the sun. He then directed the reflected light on to a sheet of paper held close to the mirror. (2019)
(a) What should he do to burn the paper?
(b) Which type of mirror does he use?
(c) Will he be able to determine the approximate value of focal length of this mirror from this activity ? Give reason and draw ray diagram to justify your answer in this case.
 View Answer
View Answer 
Ans:
(a) The student should adjust the distance between the mirror and the paper so that solar rays are sharply focussed on the paper.
(b) The mirror is a concave mirror.
(c) The student can find the approximate focal length by measuring the distance between the paper and the mirror.
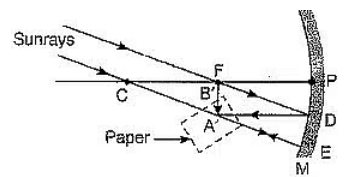
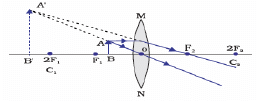
As shown in Fig. 10.29, parallel rays from the sun are focussed on the paper at point A' in focal plane of mirror such that PB' = f.
Q4: A real image, 2/3 rd of the size of an object, is formed by a convex lens when the object is at a distance of 12 cm from it. Find the focal length of the lens. (2019)
 View Answer
View Answer 
Ans: Here distance of the object from the lens u = - 12 cm and magnification of real image m = -2/3
As per relation m = v/u, we have v = mu =(-2/3) x (-12) = + 8 cm
So as per lens formula 1v - 1u = 1f
We have 1f = 1(+8) - 1(-12) = 18 + 112 = 524
Hence, f = 245 = 4.8 cm
Q5: Draw a ray diagram to show refraction through a rectangular glass slab. How is the emergent ray related to incident ray ? What is its lateral displacement ? (2019)
 View Answer
View Answer 
Ans: A ray diagram showing refraction through a rectangular glass slab has been shown in adjoining Fig.
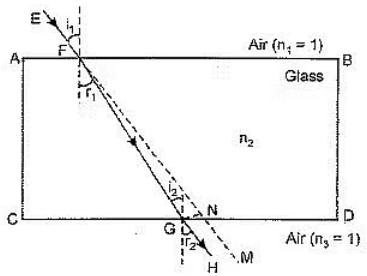
The emergent ray GH is exactly parallel to the incident ray EFNM. It means that ∠r2 = ∠i1.
However, the emergent ray is laterally (side ways) displaced as compared to the original path of light ray. In ray diagram, the lateral displacement is GN. Its value increases on increasing the width of glass slab.
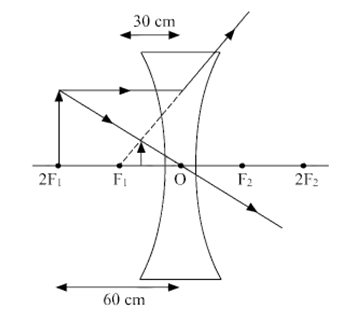
Q6: An object is placed at a distance of 60 cm from a concave lens of focal length 30 cm. (2019)
(i) Use the lens formula to find the distance of the image from the lens.
(ii) List four characteristics of the image (nature, position, size, erect/inverted) formed by the lens in this case.
(iii) Draw a ray diagram to justify your answer of the part (ii).
 View Answer
View Answer 
Ans: We have, (i) Object distance, u= —60 cm Focal length of the concave lens, f= —30 cm Using lens formula,
So as per lens formula 1v - 1u = 1f
We have 1v = 1(-60) = 1(-30)
Next, 1v = -130 - 160
Then, 1v = -360
Thus, v = -20 cm
The image will be formed at a distance of 20 cm in front of the lens.
(ii) Nature of the image is virtual. The position of the image is between F1 and optical center 0. Size of the image is diminished. The image is Erect.
(iii)
Q7: (a) List four characteristics of the image formed by a convex lens when an object is placed between its optical centre and principal focus.
(b) Size of the image of an object by a concave lens of focal length 20 cm is observed to be reduced to 1/3 rd of its size. Find the distance of the object from the lens. (2019)
 View Answer
View Answer 
Ans: (a) When an object is placed between the optical centre and principal focus of a convex lens, the image formed is virtual, erect and enlarged. Moreover, the image is formed on the same side of lens behind the object.
(b) Here magnification of given concave lens m = 1/3 and focal length of lens f = - 20 cm
As per relation m = v/u for a lens, we get
+13 = vu ⇒ vu = + u3
Therefore, as per sign convention followed, both u and v are -ve.
Using lens formula 1v - 1u = 1f, we have
1( -u/3 ) - 1( -u/20 ) ⇒ -3u + 1u = -120 ⇒ -2u = -120
Therefore, u = 40 cm
So the object is placed at a distance of 40 cm from the lens.
Previous Year Questions 2018
Q1: State the laws of refraction of light. Explain the term ‘absolute refractive index of a medium’ and write an expression to relate it with the speed of light in vacuum. (2018)  View Answer
View Answer 
Ans: Laws of refraction:
a. The incident ray, refracted ray and normal to the point of incidence all lie in the same plane.
b. The ratio of sin of incident angle to sin of angle of refraction for a given pair of medium is constant.
Sin iSin r = Constant
Absolute refractive index of a medium is the ratio of speed of light in air or vacuum to speed of light in the medium.
Absolute refractive index
= Speed of light in air/vacuumSpeed of light in Medium
Q2: What is meant by power of a lens? Write its SI unit. A student uses a lens of focal length 40 cm and another of -20 cm. Write the nature and power of each lens. (2018)
 View Answer
View Answer 
Ans: Power of lens is the ability of a lens to converge or diverge light rays passing through it. It is the reciprocal of the focal length. S.I. Unit: The Unit of power of a lens is Dioptre (D)
P = 1f(D)
Power of first lens: Focal length = +40 cm. Focal length is positive, hence it is a convex lens.
P1 = 100f(cm) = 10040 cm = +2.5 D
Power of second lens:
Focal length = -20 cm. Its focal length is negative, hence it is a concave lens.
f2 = -20100 m = -15 m
P2 = 1f2 = -5D
Q3: An object of height 4.0 cm is placed at a distance of 30 cm from the optical centre ‘O’ of a convex lens of focal length 20 cm. Draw a ray diagram to find the position and size of the image formed. Mark optical centre ‘O’ and principal focus ‘F’ on the diagram. Also find the approximate ratio of size of the image to the size of the object. (2018)
 View Answer
View Answer 
Ans: Ray diagram: Position of O and F
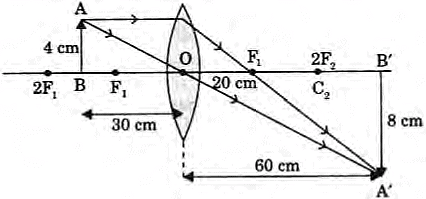
1f = 1v - 1u ⇒ 120 = 1v - 1(-30)
1v = 120 - 130 ⇒ 1v = 360 - 260
Thus, v = 60 cm
m = hiho = vu ⇒ hi4 = 60(-30)
hi = - 8 cm
Ratio = hi/ho is approximately 2:1Previous Year Questions 2017
Q1: If the image formed by a mirror for all positions of the object placed in front of it is always erect and diminished, what type of mirror is it ? Draw a ray diagram to justify your answer. Where and why do we generally use this type of mirror? (2017)
Q2: An object 4 cm in height, is placed at 15 cm in front of a concave mirror of focal length 10 cm. At what distance from the mirror should a screen be placed to obtain a sharp image of the object. Calculate the height of the image. (2017)
 View Answer
View Answer 
Ans: Here distance of object u = - 15 cm, height of object h = +4 cm and the focal length of concave mirror f = - 10 cm.
As per mirror formula 1v + 1u = 1f
We have 1v = 1(-10) = 1(-15) = 130 ⇒ u = -30 cm.
Thus, a screen is placed in front of the mirror at a distance of 30 cm from it.
Hence, magnification m = hiho = -vu
Thus, h = -vu × h = (-30)(-15) × 4 = -8 cm.
Thus, the image is an inverted image of height 8 cm.
Q3: An object is placed at a distance of 15 cm from a concave lens of focal length 30 cm. List four characteristics (nature, position, etc.) of the image formed by the lens. (2017)
 View Answer
View Answer 
Ans: Here, object distance, u = -15 cm
Using lens formula,
1f = 1v - 1u
1-30 = 1v - 1-15
1v = 1-30 - 115
Thus, v = -10 cm
Magnification, m = u/v = -10/-15 = +23
Four characteristics of the image formed by the concave lens are :
(i) Image formed is virtual
(ii) Image is erect
(iii) Image is formed on the same side of the lens as the object
(iv) Image is smaller than the object
Q4: Give any two applications of a concave and convex mirror. (2017)
 View Answer
View Answer 
Ans: (i) Concave mirrors:
- Concave mirrors are used while applying make–up or shaving, as they provide a magnified image.
- They are used in torches, search lights, and head lights as they direct the light to a long distance.
(ii) Convex mirrors:
- Convex mirrors are used in vehicles as rearview mirrors because they give an upright image and provide a wider field of view as they are curved outwards.
- They are found in the hallways of various buildings including hospitals, hotels, schools, and stores. They are usually mounted on a wall or ceiling where hallways make sharp turns.
Q5: Define power of a lens. (2017)
 View Answer
View Answer 
Ans: Power is the ability of lens to converge or diverge the ray of light is called power of lens. It is equal to the reciprocal of focal length, i.e. P = 1/f
Q6: The magnification of an image formed by a lens is -1. If the distance of the image from the optical centre of the lens is 25 cm, where is the object placed? Find the nature and focal length of the lens. If the object is displaced 15 cm towards the optical centre of the lens, where would the image be formed? Draw a ray diagram to justify your answer. (2017)
 View Answer
View Answer 
Ans: Magnification,
Image distance,
Calculate Object Position:
For a real image,
Magnification formula:
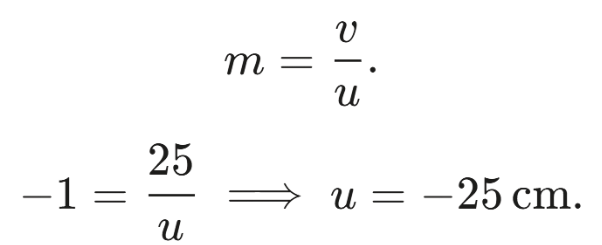 So, the object is placed at
So, the object is placed at
v=+25cm indicates a real image (right of lens), u is negative (object left of lens).Calculate Focal Length
Using the lens formula:
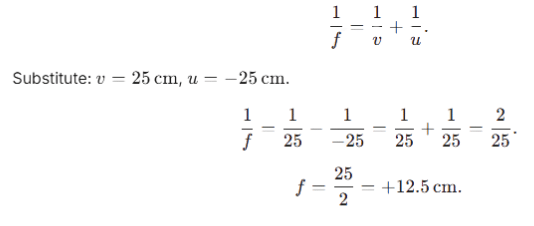 The positive focal length indicates the lens is convex with a focal length of New Image Position After Displacement
The positive focal length indicates the lens is convex with a focal length of New Image Position After Displacement
If the object is shifted 15cm towards the optical centre, the new object distance is:
Q7: If the image formed by a lens for all positions of an object placed in front of it is always erect and diminished, what is the nature of this lens? Draw a ray diagram to justify your answer. If the numerical value of the power of this lens is 10 D, what is its focal length in the Cartesian system? (2017)
Q8: Define the term magnification as referred to spherical mirrors. If a concave mirror forms a real image 40 cm from the mirror, when the object is placed at a distance of 20 cm from its pole, find the focal length of the mirror. [Delhi 2017 C]
 View Answer
View Answer 
Ans: Magnification of spherical mirror (m): It is equal to the ratio of size (height) o f the image to the size (height) of the object. Thus,
m = Size of Image (h2)/Size of Object (h1)
Given: For concave mirror u = - 20 cm,v = - 40 cm,
Using mirror equation,
1/f = 1/v + 1/u
or
1/f = 1/-40 + 1/-20
= -(1/40 + 1/20)
= -3/40
⇒ f = - 40/3
Q9: State Snell's law of refraction of light. Express it mathematically. Write the relationship between absolute efractive index of a medium and speed of light in vacuum. [AI 2017 C]
 View Answer
View Answer 
Ans: Snell’s law: The ratio of sine of angle of incidence (i.e. sin i) to the sine of angle of refraction (i.e. sin r) is always constant for the light of given colour and for the given pair of media.
Mathematically, sin i/ sin r = constant = n21
The constant n21 is called refractive index of the second medium with respect to the first medium.
Absolute refractive index of the medium is given by nm = Speed of light in vacuum (c)/ Speed of light in medium (v) = c/v
Q10: (a) What is the minimum number of rays required for locating the image formed by a concave mirror for an object? Draw a ray diagram to show the formation of a virtual image by a concave mirror.
(b) The linear magnification produced by a spherical mirror is +3. Analyze this value and state the (i) type of mirror and (ii) position of the object with respect to the pole of the mirror. Draw ray diagram to show the formation of image in this cased
(c) An object is placed at a distance of 30 cm in front of a convex mirror of focal length 15 cm. Write four characteristics of the image formed by the mirror. (2017)
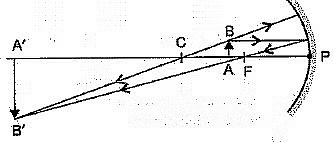
Q11: (a) To construct a ray diagram we use two rays which are so chosen that it is easy to know their directions after reflection from the mirror. List two such rays and state the path of these rays after reflection in case of concave mirrors. Use these two rays and draw ray diagram to locate the image of an object placed between pole and focus of a concave mirror.
(b) A concave mirror produces three times magnified image on a screen. If the object is placed 20 cm in front of the mirror, how far is the screen from the object? (2017)
 View Answer
View Answer 
Ans: (a) Rays which are chosen to construct a ray diagram for reflection are: A ray parallel to the principal axis and A ray passing through the centre of curvature of a concave mirror.
Path of these light rays after reflection:
(i) It will pass through the principal focus of a concave mirror
(ii) It gets reflected back along the same path. When an object is placed between the pole and the principal focus of a concave mirror, a virtual, erect and enlarged image is formed behind the concave mirror as shown in the figure.
(b) m=−3,
u=−20 cm u = -20 \, \text{cm} cm ,
v=? v = ?
Image Position
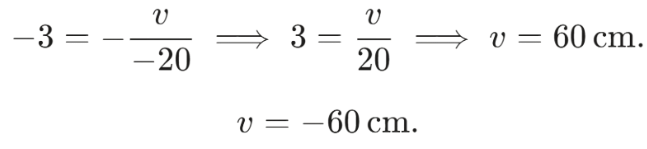
Distance Between Screen and Object
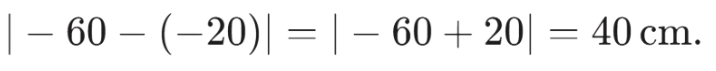
Answer:
Distance = 40 cm 40 \, \text{cm} cm.
Q12: Analyse the following observation table showing variation of image-distance (v) with object-distance (u) in case of a convex lens and answer the questions that follow without doing any calculations: (2017)
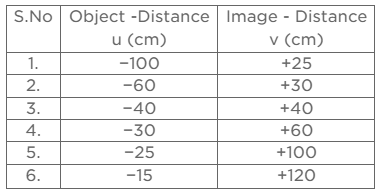 (a) What is the focal length of the convex lens? Give reason to justify your answer.
(a) What is the focal length of the convex lens? Give reason to justify your answer.
(b) Write the serial number of the observation which is not correct. On what basis have you arrived at this conclusion?
(c) Select an appropriate scale and draw a ray diagram for the observation at S.No. 2. Also find the approximate value of magnification.
Q13: (a) If the image formed by a mirror for all positions of the object placed in front of it is always diminished, erect and virtual, state the type of the mirror and also draw a ray diagram to justify your answer. Write one use such mirrors are put to and why?
(b) Define the radius of curvature of spherical mirrors. Find the nature and focal length of a spherical mirror whose radius of curvature is +24 cm. (2017)
 View Answer
View Answer 
Ans: (a) Convex (diverging) mirror
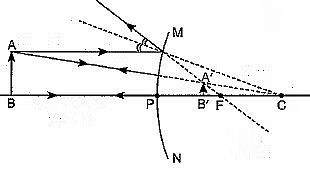
Reason: (i) It always produces a virtual and erect image.
(ii) The size of image formed is smaller than the object.
Therefore, it enables the driver to see a wide field view of the traffic behind the vehicle in a small mirror.
(b) Radius of Curvature: The separation between the pole and the centre of curvature or the radius of the hollow sphere, of which the mirror is a part, is called radius of curvature (R), i.e., PC = R.
Since focal length of the mirror is +24 cm. It indicates that nature of the given spherical mirror is convex/diverging mirror.
As R = 2f = 24 cm
Therefore, f = +12 cm
Q14: (a) Draw labelled ray diagrams for each of the following cases to show the position, nature and size of the image formed by a convex lens when the object is placed. (2017)
(i) between its optical center (O) and principal focus (F)
(ii) between F and 2 F
(b) How will the nature and size of the image formed in the above two cases, (i) and (ii) change, if the convex lens is replaced by a concave lens of same focal length?
Q15: State the laws that are followed when light is reflected by spherical mirrors. Draw a ray diagram to show the formation of image of an object placed in front of a convex mirror. List two characteristics of the image formed. Briefly explain one use of convex mirrors. (2017)
 View Answer
View Answer 
Ans: Laws of reflection
(i) The incident ray, reflected ray and normal to the reflecting surface at the incident point all lie in the same plane.
(ii) The angle of reflection is equal to the angle of incidence.
Characterstics of the Image:
(1) The convex mirror always form virtual and erect images.
(2) The size of the image is always lesser than the object.
Use of convex mirror-
This mirror is used in vechiles mirror to see the nearer object to vechicle.
Q16: A student carries out the experiment of tracing the path of a ray of light through a rectangular glass slab for two different values of angle of incidence ∠i = 30º and ∠i = 45°. In the two cases the student is likely to observe the set of values of angle of refraction and angle of emergence as:
(a) ∠r =30º, ∠e = 20º and ∠r = 45º, ∠e = 28º
(b) ∠r =30º, ∠e = 30º and ∠r = 45º, ∠e = 45º
(c) ∠r =20º, ∠e = 30º and ∠r = 28º, ∠e = 45º
(d) ∠r =20º, ∠e = 20º and ∠r = 28º, ∠e = 28º (CBSE 2017)
 View Answer
View Answer 
Ans: (c)
In an experiment involving a rectangular glass slab, when light passes through it, the angle of incidence (∠i) and angle of emergence (∠e) are equal. However, the angle of refraction (∠r) inside the glass slab is different due to the change in the medium's refractive index.
For two different angles of incidence (∠i = 30°∠i = 30° and ∠i = 45°∠i = 45°):
- When ∠i = 30°, the angle of refraction ∠r will be smaller due to the denser medium, resulting in ∠r ≈ 20°∠r ≈ 20°. As the ray emerges from the glass, the angle of emergence ∠e will be equal to the angle of incidence, so ∠e = 30°.
- When ∠i = 45°∠i = 45°, the angle of refraction ∠r will be approximately 28°. Again, the angle of emergence ∠e will match the angle of incidence, so ∠e = 45°∠e = 45°.
Therefore, the correct set of values is (c) ∠r = 20º, ∠e = 30º and ∠r = 28º, ∠e = 45º.
Previous Year Questions 2016
Q1: What is a prism? (2016)  View Answer
View Answer 
Ans: A prism is an optical device with two triangular bases along with three rectangular lateral surfaces commonly inclined at an angle of 60°.
Q2: Define the term reflection. (2016)
 View Answer
View Answer 
Ans: The bouncing back of a ray of light in the same medium after striking on a surface of an object.
Q3: The nature, size and position of image of an object produced by a lens or mirror are as shown below. Identify the lens/ mirror (X) used in each case and draw the corresponding complete ray diagram, (size of the object about half of the image). (2016)
Q4: (a) Calculate the distance at which an object should be placed in front of a convex lens of focal length 10 cm to obtain a virtual image of double its size.
(b) In the above given case, find the magnification, if image formed is real. Express it in terms of relation between v and u (2016)
 View Answer
View Answer 
Ans: Given f = + 10 cm, u = ?
For virtual image
m = + 2
As
m = v/u or v/u = 2
v = 2u ...(1)
1/v = 1/u = 1/f ...(2)
Substituting (1) in (2)
12u - 1u = 110
12u = 110
u = -5 cm
For real image, f = 10 cm, m = -2
vu = -2, v = -2u
1v - 1u = 1f
1(-2u) - 1u = 110
-3/2u = 1/10 or u = -15 cm
Q5: One half of a convex lens is covered with a black paper. (2016)
a. Show the formation of image of an object placed at 2Fp of such covered lens with the help of ray diagram. Mention the position and nature of image.
b. Draw the ray diagram for same object at same position in front of the same lens, but now uncovered. Will there be any difference in the image obtained in the two cases? Give reason for your answer.
Q6: State the relation between object distance, image distance and focal length of a concave or convex mirror. A concave mirror produces two times magnified real image of an object at 10 cm from it. Find the position of the image. (2016)
 View Answer
View Answer 
Ans: For concave or convex mirrors the relation between u, v and f is given by
mirror formula,
1v - 1u = 1f
m = - 2
u = - 10 cm
m = - v/u = - 2 or v = 2u = -20 cm
v = - 20 cm
Q7: (A) One-half of a convex lens is covered with a black paper. Will this lens produce a complete image of the object? Verify your answer experimentally. Explain your observations.
(B) Name the lens which can be used as a magnifying glass. (CBSE 2016)
 View Answer
View Answer 
Ans: (A) Yes, even when one half of the convex lens is covered with a black paper, the complete image of the object will be formed. When the upper half of the lens is covered: In this situation, rays of light coming from the object will be refracted by the lower half of the lens as shown in fig (a). These rays meet at the other side of the lens to form the image of the given object. When the lower half of the lens is covered: In this situation, rays of light coming from the object will be refracted by the upper half of the lens. These rays meet at the other side of the lens to form the image of the given object, as shown in the figure (b). We will get a sharp image but the brightness of the image will be less now.
Ray diagram:
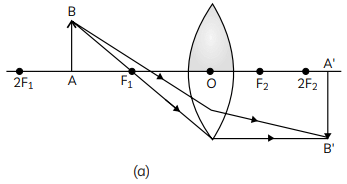
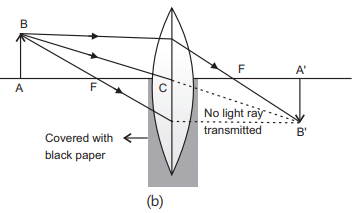
(B) Convex lens can be used as a magnifying glass.
Q8: Suppose you have three concave mirrors A, B and C of focal lengths 10 cm, 15 cm and 20 cm. For each concave mirror you perform the experiment of image formation for three values of object distance of 10 cm, 20 cm and 30 cm. Giving reason answer the following:
(A) For the three object distances, identify the mirror/mirrors which will form an image of magnification –1.
(B) Out of the three mirrors identify the mirror which would be preferred to be used for shaving purposes/makeup.
(C) For the mirror B draw ray diagram for image formation for object distances 10 cm and 20 cm. (CBSE 2016)
 View Answer
View Answer 
Ans: (A) A real, inverted and same size image as that of object, formed by the concave mirror, will form an image of magnification –1. It is possible only when the object is placed at C (R = 2f). Hence, for the object distances of 20 cm and 30 cm, concave mirrors ‘A’ and ‘B’ will form the real, inverted and same size images as that of the object. Therefore, the mirrors ‘A’ and ‘B’ will form an image of magnification –1.
(B) Concave mirror of focal length 20 cm will be preferred to be used for shaving purpose or makeup. This is because when we bring our face within its focal length it forms a virtual, erect and enlarged image of our face.
(C) Ray diagram for image formation by mirror ‘B’
(i) For object distance 10 cm.
(ii) For object distance 20 cm.
Previous Year Questions 2015
Q1: What is the magnification of the images formed by plane mirrors and why? (2015)  View Answer
View Answer 
Ans: Magnification of images formed by plane mirrors is unity because for plane mirrors, the size of the image formed is equal to that of the object.
Q2: What is meant by power of a lens? (2015)
 View Answer
View Answer 
Ans: Power is the degree of convergence or divergence of light rays achieved by a lens.
It is defined as the reciprocal of its focal length. i.e, P = 1/f
Q3: Name the mirror that is used by a dentist in examining teeth. (2015)
 View Answer
View Answer 
Ans: Dentist uses a concave mirror to see large images of the teeth of patients.
Q4: What is lateral displacement of a light ray passing through a glass slab? (2015)
 View Answer
View Answer 
Ans: The shifting of the light ray sideways (though in the direction of original ray) on emergence from a rectangular glass slab is called “lateral displacement”.
Q5: Define power of a lens and write its SI unit. (2015)
 View Answer
View Answer 
Ans: Reciprocal of focal length of a lens, expressed in meter, is called the power of that lens.
Its SI unit is 1 dioptre (1 D), where 1 D = 1 m-1.
Q6: Name the lens which can be used as a magnifying glass. (2015)
 View Answer
View Answer 
Ans: A convex lens can be used as a magnifying glass so as to form magnified image of a tiny object placed near it.
Q7: Which type of lens has a negative power? (2015)
 View Answer
View Answer 
Ans: A concave (diverging) lens has a negative power.
Q8: What is the difference between virtual image of an object formed by a convex lens and that formed by a concave lens? (2015)
 View Answer
View Answer 
Ans: 'Virtual image formed by a convex lens is always magnified but that formed by a concave lens is diminished one.
Q9: During its passage from one medium to another, where does a light ray change its path? (2015)
 View Answer
View Answer 
Ans: During its passage from one medium to another a light ray changes its path at the boundary face separating the two media.
Q10: The power of a lens is + 5 D. Find its focal length in metres. (2015)
Q11: What are the units of power of a lens? (2015)
 View Answer
View Answer 
Ans: If the focal length is measured in metre then the unit of power of a lens is dioptre.
Q12: If the image formed by a mirror for all positions of the object placed in front of it is always erect and diminished, what type of mirror is it? Draw a ray diagram to justify your answer. Where and why do we generally use this type of mirror? (2015)
Q13: Name the type of mirror used in the following: (2015)
a. Solar furnace
b. Side/rear - view mirror of a vehicle.
Draw a labelled ray diagram to show the formation of image in each of the above two cases.
Which of these mirrors could also form a magnified and virtual image of an object? Illustrate with the help of a ray diagram.
Previous Year Questions 2014
Q1: Write down four important characteristics of image formed by a plane mirror. (2014)  View Answer
View Answer 
Ans: The characteristics of an image formed by a plane mirror are:
- The image is virtual.
- The image is erect.
- The image is laterally inverted.
- The size of the image is equal to that of the object.
Q2: Describe a spherical mirror. (2014)
Q3: Define the following terms in relation to concave spherical mirror: (2014)
(a) Pole
(b) Centre of curvature
(c) Radius of curvature
(d) Principal axis
(e) Principal focus
(f) Aperture
(g) Focal length
 View Answer
View Answer 
Ans: (a) The mid point of mirror is known as pole.
(b) The centre of curvature of a spherical mirror is the centre of that sphere of which mirror is a part,
(c) The distance between pole and centre of curvature is called radius of curvature of the mirror.
(d) The straight line joining the pole and centre of curvature is called principal axis.
(e) The point on the principal axis through which parallel rays to the principal axis passes or appear to pass after reflection.
(f) The diameter of the mirror or size of the mirror is called aperture.
(g) The distance between focus and pole of a mirror is the focal length of the mirror.
Q4: With the help of ray diagram show that angle of incidence is equal to the angle of reflection when a ray is incident on the concave/convex mirror. (2014)
Q5: A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of image and magnification. Describe what happens to the image as the needle is moved farther from the mirror. (2014)
Previous Year Questions 2013
Q1: The path of a ray of light coming from air passing through a rectangular glass slab is traced by four students shown as A, B, C and D in the figures. Which one of these is correct?
(a) 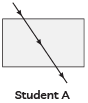
(b) 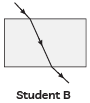
(c) 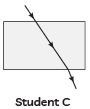
(d) 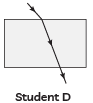 (CBSE 2013, 11)
(CBSE 2013, 11)
 View Answer
View Answer 
Ans: (b)
When light passes through a rectangular glass slab from air, it bends towards the normal upon entering the glass due to refraction. Inside the glass slab, the ray travels in a straight line parallel to the initial direction but displaced laterally. Upon exiting the glass slab into air, it bends away from the normal and emerges parallel to the original incident ray.
In the diagrams:
- Student B shows the correct path of the light ray with lateral displacement and emergence parallel to the incident ray.
- The other diagrams do not show the correct behavior of refraction through a rectangular glass slab.
Thus, the correct answer is (b) Student B.




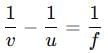
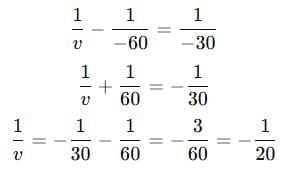


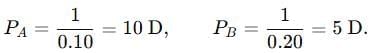

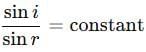 for a given pair of media and light colour. This constant is the refractive index of the second medium with respect to the first (Snell’s law).
for a given pair of media and light colour. This constant is the refractive index of the second medium with respect to the first (Snell’s law).
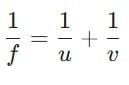
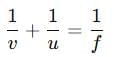 For a concave mirror take u = -10 cm (object to the left) and f = -15 cm. Substitute:
For a concave mirror take u = -10 cm (object to the left) and f = -15 cm. Substitute: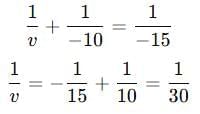 so, v = +30 cm.
so, v = +30 cm.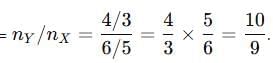
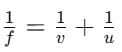
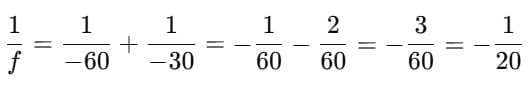
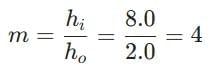
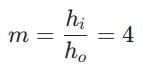 and
and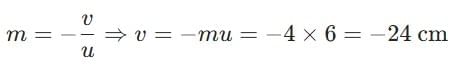
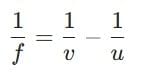

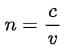
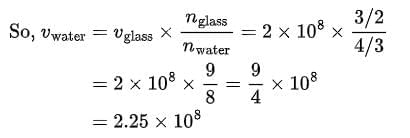
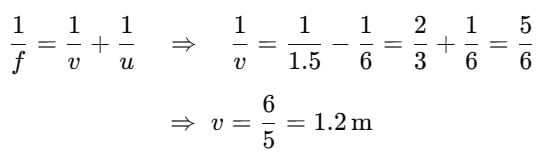
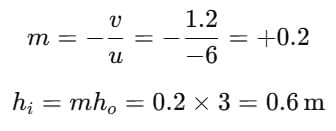
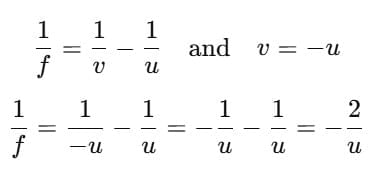
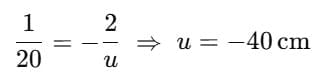 (Sign ‘−’ means the object is placed on the incoming-light side; distance = 40 cm.)
(Sign ‘−’ means the object is placed on the incoming-light side; distance = 40 cm.)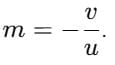
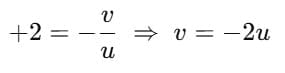 Mirror formula:
Mirror formula: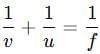
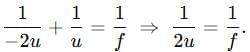

 (b) Redraw the path of a ray of light through the three media, if the ray of light starting from medium A falls on the medium B:
(b) Redraw the path of a ray of light through the three media, if the ray of light starting from medium A falls on the medium B:
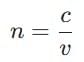
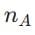
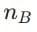
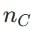
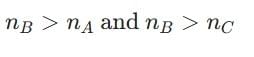
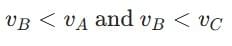
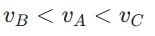

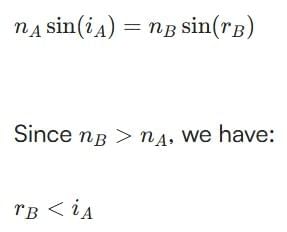
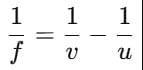


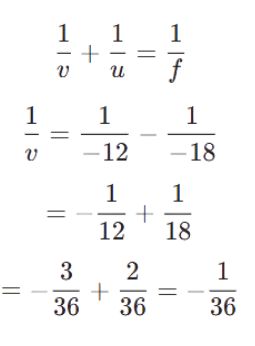 v = -36 cm
v = -36 cm




 (2) is directed towards its principal focus
(2) is directed towards its principal focus (ii) Given u = –16 cm, f = + 24 cm, h = 4 cm
(ii) Given u = –16 cm, f = + 24 cm, h = 4 cm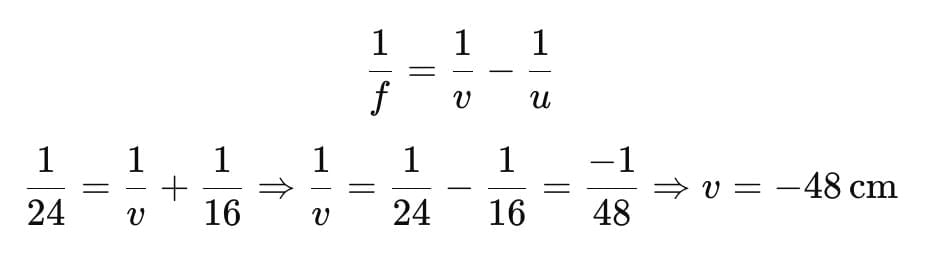
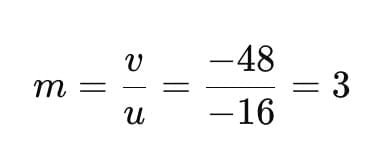
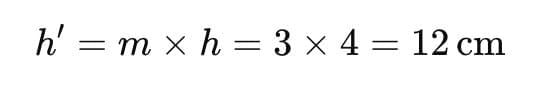
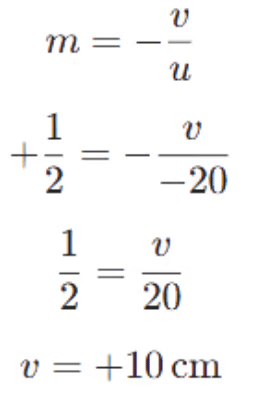 The image is at
The image is at 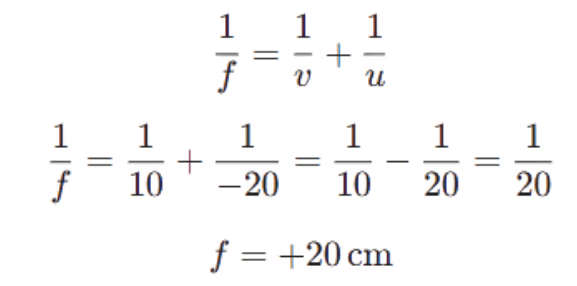 The positive focal length indicates a convex mirror, consistent with the positive magnification.
The positive focal length indicates a convex mirror, consistent with the positive magnification.
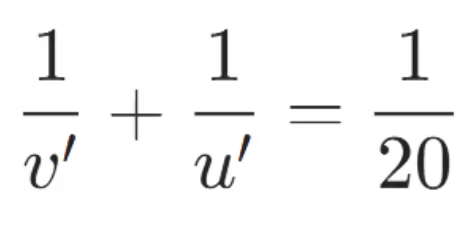
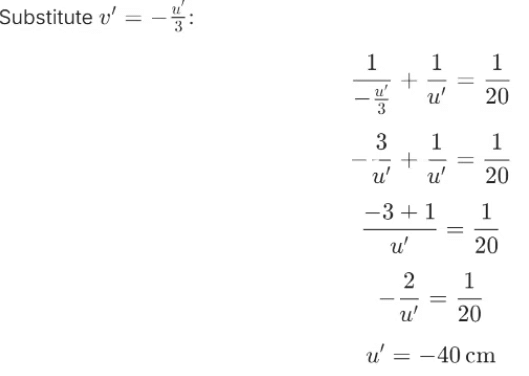
 The magnification is +1/3, as required.
The magnification is +1/3, as required.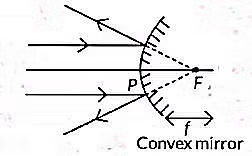

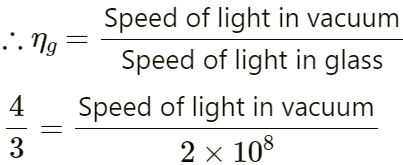
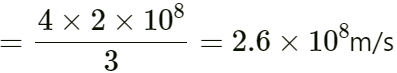
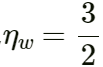
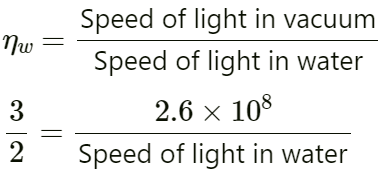




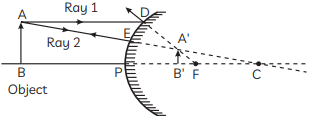 (B) The image of object obtained in the convex mirror is erect and diminished. This is because a convex mirror always forms a virtual, erect and diminished image of an object.
(B) The image of object obtained in the convex mirror is erect and diminished. This is because a convex mirror always forms a virtual, erect and diminished image of an object. 
 (a) Image formed is real.
(a) Image formed is real.










 (a) Is the type of lens used converging or diverging?
(a) Is the type of lens used converging or diverging? 





 The image formed is real, inverted and of the same size.
The image formed is real, inverted and of the same size.




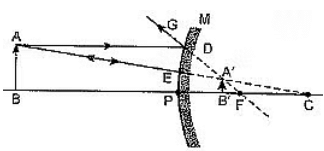
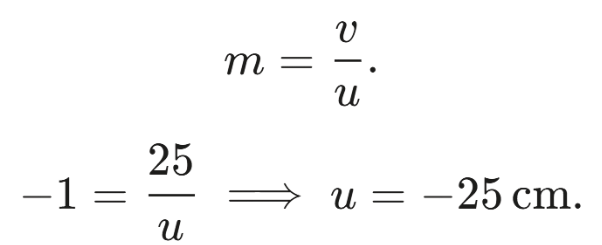 So, the object is placed at
So, the object is placed at 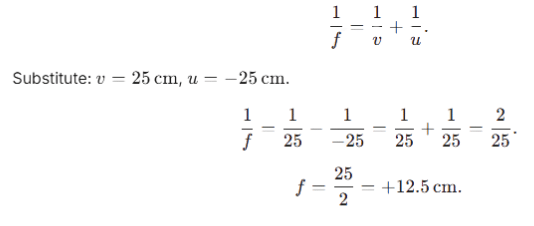 The positive focal length indicates the lens is convex with a focal length of New Image Position After Displacement
The positive focal length indicates the lens is convex with a focal length of New Image Position After Displacement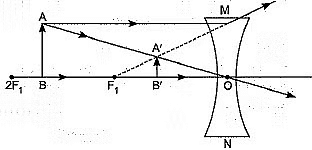
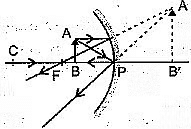
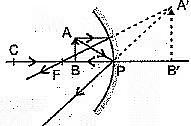 (c) The four characteristics of the image formed by the convex mirror are virtual, erect, diminished and laterally inverted.
(c) The four characteristics of the image formed by the convex mirror are virtual, erect, diminished and laterally inverted.
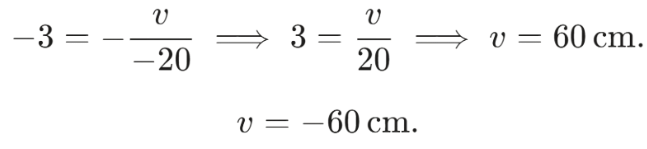
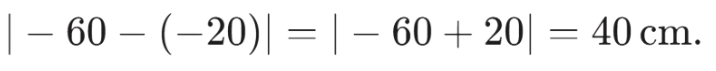
 (a) What is the focal length of the convex lens? Give reason to justify your answer.
(a) What is the focal length of the convex lens? Give reason to justify your answer. 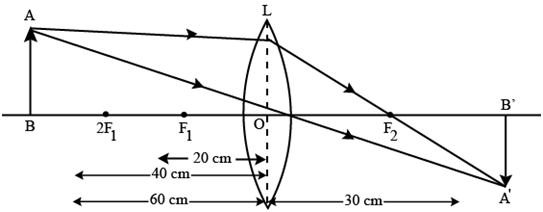

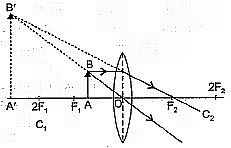
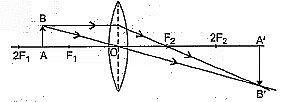


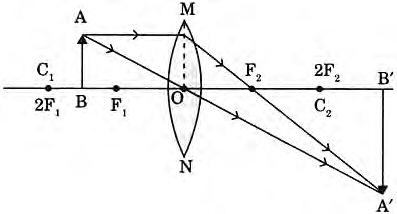
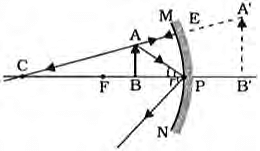
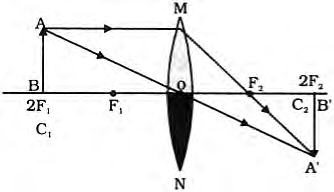




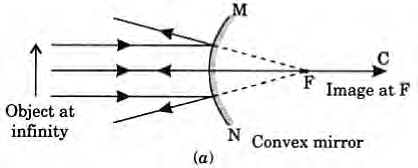
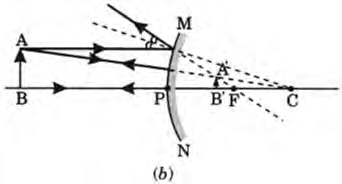
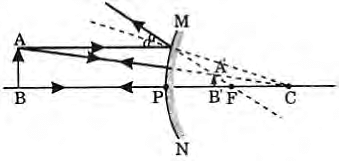
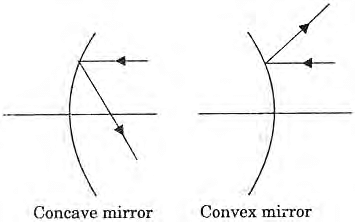
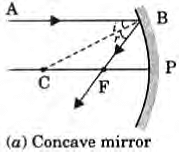
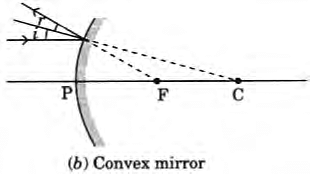




 (CBSE 2013, 11)
(CBSE 2013, 11)




















