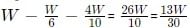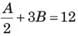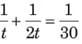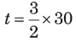Time & Work CAT Previous Year Questions with Answer PDF
From 2015 to 2024, the CAT exam included questions on quantitative reasoning, focusing on time and work problem-solving skills. The 2023 exam also featured quantitative reasoning questions, continuing the trend of testing analytical abilities through work-related problems, while earlier years like 2022, 2021, 2019, 2018, 2017, 2016, and 2015 similarly incorporated such challenges.
2024
Q1: Renu would take 15 days working 4 hours per day to complete a certain task whereas Seema would take 8 days working 5 hours per day to complete the same task. They decide to work together to complete this task. Seema agrees to work for double the number of hours per day as Renu, while Renu agrees to work for double the number of days as Seema. If Renu works 2 hours per day, then the number of days Seema will work, is
Ans: 6
Sol: Let Renu and Seema do r and s
units of work daily.ATQ,
r × 15 × 4 = s × 8 × 5
r / s = 2 / 3
Let the total number of work be 120 units.
So, Renu’s one day’s work = 2 units
Seema’s one day’s work = 3 units
Now, according to new agreement:
Renu works 2 hours a day for 2d while Seema works 4 hours a day for d days.
So,
2 × 2 × 2d + 3 × 4 × d = 120
20d = 120
d = 6 days
Hence, Seema works for 6 days.
Q2: Amal and Vimal together can complete a task in 150 days, while Vimal and Sunil together can complete the same task in 100 days. Amal starts working on the task and works for 75 days, then Vimal takes over and works for 135 days. Finally, Sunil takes over and completes the remaining task in 45 days. If Amal had started the task alone and worked on all days, Vimal had worked on every second day, and Sunil had worked on every third day, then the number of days required to complete the task would have been
Ans: 139
Sol: Let the work done by Amal, Vimal and Sunil be x, y and z, respectively.
Let the total work be w
Now, according to the question,
150x + 150y = w ...(1)
100y + 100z = w ...(2)
75x + 135y + 45z = w ...(3)
Adding (1) and (2), we get,
150x + 250y + 100z = 2w ...(4)
Multiplying (3) with 2 we get: 150x + 270y + 100z = 2w ...(5)
Subtracting (5) from (4), we get 10z = 20y or simply z = 2y
Using this in (2), we get w = 300y, and using w = 300y in (1), we get x = y
So, the work done by Amal, Vimal and S equals y, y, and 2y units per day.
In 6 days, Amal will work for 6 days, doing 6y units of work.
Vimal will work for 3 days, doing 3y units of work.
Sunil will work for 2 days, doing 4y units of work.
So, in one 6-day cycle, 13y units of work will be done.
Dividing the total work (300y) by 13y, we can see that the total of 23 cycles with 299V units of work will be done.
These 23 cycles will be 23 x 6 = 138 days
The remaining 1 unit of work will be done in the next day.
So, a total of 139 days will be required.
Hence, 139 is the required answer.
Q3: Sam can complete a job in 20 days when working alone. Mohit is twice as fast as Sam and thrice as fast as Ayna in the same job. They undertake a job with an arrangement where Sam and Mohit work together on the first day, Sam and Ayna on the second day, Mohit and Ayna on the third day, and this three-day pattern is repeated till the work gets completed. Then, the fraction of total work done by Sam is
(a) 1/5
(b) 3/10
(c) 1/20
(d) 3/20
Ans: b
Sol: Let's take the total work as any multiple of 20. Let the total work be 60 unit
Efficiency of Sam = 60/20 = 3 unit/d
Eff of Mohit = 6 unit/day
Eff of Ananya = 2 unit/day
for first day Sam + Mohit do work, so total unit of work done in first day = 9 unit
for second day Sam + Ananya, unit of work done in second day = 5 unit
for third day Mohit + Ananya, unit of work done in third day = 8 unit
This pattern is repeated, then in 6 days total 44 units of work will be done and chance of Sam will come 4 times in these 6 days so the work done by Sam in these 6 days = 4 x 3 = 12
After 44 units 16 units are left
Now first Sam + Mohit will work = 9 unit
and then Sam + Ananya will work = 5 unit
and then rest of work will be done Mohit and Ananya. AS we need only Sam' work fraction so we will consider that only
So Sam will do 12 + 3 + 3 = 18 unit of work till completion of job
So fraction of Sam's work = 18/60 = 3/10
2023
Q1: The amount of job that Amal, Sunil and Kamal can individually do in a day, are in harmonic progression. Kamal takes twice as much time as Amal to do the same amount of job. If Amal and Sunil work for 4 days and 9 days, respectively, Kamal needs to work for 16 days to finish the remaining job. Then the number of days Sunil will take to finish the job working alone, is [2023]
Ans: 27
Sol: “The amount of job that Amal, Sunil and Kamal can individually do in a day, are in harmonic progression.” This implies that the amount of time taken individually by Amal, Sunil and Kamal to finish a job are in A.P.
“Kamal takes twice as much time as Amal to do the same amount of job.” Since the amount of time taken individually by Amal, Sunil and Kamal to finish a job are in A.P, this simply means that Sunil Should take 1.5 times the time as Amal to do the same amount of job.
So, to do the same amount of job individually, the times taken by Amal, Sunil and Kamal will be in the ratio, 1 : 1.5 : 2 or 2 : 3 : 4
Amal, Sunil and Kamal worked for 4, 9 and 16 days respectively to finish the job.
Sunil does in 3 days what Amal does in 2 days.
Therefore, Sunil does in 6 days what Amal does in 4 days.
Sunil does in 3 days what Kamal does in 4 days.
Therefore, Sunil does in 12 days what Kamal does in 16 days.
So, to finish the entire job on his own, Sunil would require, 6 + 9 + 12 = 27 days.
Q2: Rahul, Rakshita and Gurmeet, working together, would have taken more than 7 days to finish a job. On the other hand, Rahul and Gurmeet, working together would have taken less than 15 days to finish the job. However, they all worked together for 6 days, followed by Rakshita, who worked alone for 3 more days to finish the job. If Rakshita had worked alone on the job then the number of days she would have taken to finish the job, cannot be [2023]
(a) 20
(b) 17
(c) 16
(d) 21
Ans: (d)
Sol: Let the work done byRahul, Rakshita, and Gurmeet be a, b, and c units per day, respectively, and the total units of work are W.
Hence, we can say that 7(a + b + c) < W (Rahul, Rakshita, and Gurmeet, working together, would have taken more than 7 days to finish a job).
Similarly, we can say that 15(a + c) > W (Rahul and Gurmeet, working together would have taken less than 15 days to finish the job)
Now, comparing these two inequalities, we get: 7(a + b + c) < W < 15(a + c)
It is also known thatthey all worked together for 6 days, followed by Rakshita, who worked alone for 3 more days to finish the job.
Therefore, the total units of work done is: W = 6(a + b + c) + 3b
Hence, we can say that7(a + b + c) <6(a + b + c) + 3b< 15(a + c)
Therefore, (a + b + c) < 3b ⇒ a + c < 2b, and 9b < 9(a + c) => b < a + c
⇒ a + b + c < 3b => 7(a + b + c) < 21b , and 15b < 15(a + c)
Hence, The number of days required for b must be in between 15 and 21 (both exclusive).
Hence, the correct option is D
2022
Q1: Working alone, the times taken by Anu, Tanu and Manu to complete any job are in the ratio 5 : 8 : 10. They accept a job which they can finish in 4 days if they all work together for 8 hours per day. However, Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day. Then, the number of hours that Manu will take to complete the remaining job working alone is [2022]
Ans: 6
Sol: Let the time taken by Anu, Tanu and Manu be 5x, 8x and 10x hours.
Total work = LCM(5x, 8x, 10x) = 40x
Anu can complete 8 units in one hour
Tanu can complete 5 units in one hour
Manu can complete 4 units in one hour
It is given, three of them together can complete in 32 hours.
32(8 + 5 + 4) = 40x
X = 68/5
It is given,
Anu and Tanu work together for the first 6 days, working 6 hours 40 minutes per day, i.e. 36 + 4 = 40 hours
40(8 + 5) + y(4) = 40x
4y = 24
y = 6
Manu alone will complete the remaining work in 6 hours.
Q2: Bob can finish a job in 40 days, if he works alone. Alex is twice as fast as Bob and thrice as fast as Cole in the same job. Suppose Alex and Bob work together on the first day, Bob and Cole work together on the second day, Cole and Alex work together on the third day, and then, they continue the work by repeating this three - day roster, with Alex and Bob working together on the fourth day, and so on. Then, the total number of days Alex would have worked when the job gets finished, is [2022]
Ans: 11
Sol: Let the efficiency of Bob be 3 units/day. So, Alex's efficiency will be 6 units/day, and Cole's will be 2 units/day.
Since Bob can finish the job in 40 days, the total work will be 40*3 = 120 units.
Since Alex and Bob work on the first day, the total work done = 3 + 6 = 9 units.
Similarly, for days 2 and 3, it will be 5 and 8 units, respectively.
Thus, in the first 3 days, the total work done = 9 + 5 + 8 = 22 units.
The work done in the first 15 days = 22*5 = 110 units.
Thus, the work will be finished on the 17th day(since 9 + 5 = 14 units are greater than the remaining work).
Since Alex works on two days of every 3 days, he will work for 10 days out of the first 15 days.
Then he will also work on the 16th day.
The total number of days = 11.
Q3: A group of N people worked on a project. They finished 35% of the project by working 7 hours a day for 10 days. Thereafter, 10 people left the group and the remaining people finished the rest of the project in 14 days by working 10 hours a day. Then the value of N is
(a) 150
(b) 36
(c) 23
(d) 140
Ans: d
Let each man do 1 unit work per hour.
70N units is 35% work.
So, 140N units is 70% work and 140(N-10) is 100-35 = 65% work
So, 1400 units is 70-65 = 5% work
1400x7 units is 35% work = 70N
=> N = 140
2021
Q1: Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is [2021]
Ans: 32
Sol: Let the total work be 48 units. Let Amar do 'm' work, Akbar do 'k' work, and Anthony do 'n' units of work in a month.
Amar and Akbar complete the project in 12 months. Hence, in a month they do 48/12 = 4 units of work.
m + k = 4.
Similarly, k+n = 3, and m+n = 2.
Solving the three equations, we get m = 3/2, k = 5/2, n = 1/2
Here, Amar works neither the fastest not the slowest, and he does 1.5 units of work in a month. Hence, to complete the work, he would take 48/1.5 = 32months.
Q2: Anu, Vinu and Manu can complete a work alone in 15 days, 12 days and 20 days, respectively. Vinu works everyday. Anu works only on alternate days starting from the first day while Manu works only on alternate days starting from the second day. Then, the number of days needed to complete the work is [2021]
(a) 5
(b) 8
(c) 6
(d) 7
Ans: (d)
Sol: Let the total amount of work be 60 units.
Then Anu, Vinu, and Manu do 4, 5, and 3 units of work per day respectively.
On the 1st day, Anu and Vinu work. Work done on the 1st day = 9 units
On the 2nd day, Manu and Vinu work. Work done on the 2nd day = 8 units
This cycle goes on. And in 6 days, the work completed is 9 + 8 + 9 + 8 + 9 + 8 = 51 units.
On the 7th day, again Anu and Vinu work and complete the remaining 9 units of work. Thus, the number of days taken is 7 days.
Q3: Anil can paint a house in 60 days while Bimal can paint it in 84 days. Anil starts painting and after 10 days, Bimal and Charu join him. Together, they complete the painting in 14 more days. If they are paid a total of ₹ 21000 for the job, then the share of Charu, in INR, proportionate to the work done by him, is [2021]
(a) 9000
(b) 9200
(c) 9100
(d) 9150
Ans: (c)
Sol: Let Entire work be W
Now Anil worked for 24 days ( 10 days alone and 14 days with bimal and charu both )
Bimal worked for 14 days and Charu worked for 14 days .
Now Anil Completes W in 60 days
so in 24 days he completed 0.4W
Bimal completes W in 84 Days
So in 14 Days Bimal completes = W/6
Therefore work done by charu =
Therefore proportion of Charu = 13/30 x 21000 = 9100
Q4: One day, Rahul started a work at 9 AM and Gautam joined him two hours later. They then worked together and completed the work at 5 PM the same day. If both had started at 9 AM and worked together, the work would have been completed 30 minutes earlier. Working alone, the time Rahul would have taken, in hours, to complete the work is [2021]
(a) 11.5
(b) 10
(c) 12.5
(d) 12
Ans: (b)
Sol: Let Rahul work at a units/hr and Gautam at b units/hour
Now as per the condition :
8a + 6b =7.5a + 7.5b
so we get 0.5a = 1.5b
or a = 3b
Therefore total work = 8a + 6b = 8a + 2a = 10a
Now Rahul alone takes 10a/10 = 10 hours.
Q5: Anil can paint a house in 12 days while Barun can paint it in 16 days. Anil, Barun, and Chandu undertake to paint the house for ₹ 24000 and the three of them together complete the painting in 6 days. If Chandu is paid in proportion to the work done by him, then the amount in INR received by him is [2021]
Ans: 3000
Sol: Now Anil Paints in 12 Days
Barun paints in 16 Days
Now together Arun , Barun and Chandu painted in 6 Days
Now let total work be W
Now each worked for 6 days
So Anil's work = 0.5W
Barun's work = 6W / 16 = 3W/8
Therefore Charu's work =W/2 - 3W/8 = W/8
Therefore proportion of charu = 24000/8 = 3,000
2019
Q1: At their usual efficiency levels, A and B together finish a task in 12 days. If A had worked half as efficiently as she usually does, and B had worked thrice as efficiently as he usually does, the task would have been completed in 9 days. How many days would A take to finish the task if she works alone at her usual efficiency? [2019]
(a) 18
(b) 36
(c) 24
(d) 12
Ans: (a)
Sol:Let Total work be 108 days
At normal efficiency work is done in 12 days
Let A' s day work = A & B' s day work = B
► A + B = 9 &
► A + B = 9…(1)
► A + 6B = 24…(2)
Solving (1) & (2), A = 6 B = 3
At usual efficiency A will do the work in 108 / 6 =18 days.
Q2: Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job, If Bimal has done 10% of the job, then in how many days was the job done? [2019]
(a) 14
(b) 15
(c) 13
(d) 12
Ans: (c)
Sol: Let total work be 40 units
Anil's day work = 2 unit
Sunil's 1 day work = 1 unit
For the first 3 days work done = 6 unit
Work done by Bimal = 4 unit
Work done by A and S during this time = 30 unit
Days = 30 / 3 = 10 days
Total days = 10 + 3 = 13 days
2018
Q1: A tank is fitted with pipes, some filling it and the rest draining it. All filling pipes fill at the same rate, and all draining pipes drain at the same rate. The empty tank gets completely filled in 6 hours when 6 filling and 5 draining pipes are on, but this time becomes 60 hours when 5 filling and 6 draining pipes are on. In how many hours will the empty tank get completely filled when one draining and two filling pipes are on? [2018]
(a) 10 hrs
(b) 12 hrs
(c) 16 hrs
(d) 18 hrs
Ans: (a)
Sol: Let the rate of each filling pipe be 'f ' litres/hr and the rate of each draining pipes be 'd' litres/hr
As per the first condition given in the question, Capacity of tank will be = (6f - 5d ) x 6 …(i)
And as per the second condition given in the question, Capacity of tank will be = (5f - 6d ) x 60 …(ii)
Since the capacity of tank is same in both the cases, on equating (i) and (ii), we have
► (6f - 5d) x 6 = (5f - 6d) x 60
► or, 6f - 5d = 50f - 60d
► or, 44f = 55d
► or, 4f = 5d
Therefore, f = 1.25d , putting this value in eq. (i),
Capacity of the tank = (6f - 5d ) x 6 = (7.5d - 5d) x 6 = 15d
When 2 filling and 1 draining pipes work simultaneously, the effective rate of filling the tank = (2f - d ),
Now putting f =1.25d in this eq. we have
Effective rate = (2.5d - d ) = 1.5d
Therefore time required to fill the empty tank = 15d / 1.5d = 10 hours.
Q2: Humans and robots can both perform a job but at different efficiencies. Fifteen humans and five robots working together take thirty days to finish the job, whereas five humans and fifteen robots working together take sixty days to finish it. How many days will fifteen humans working together (without any robot) take to finish it? [2018]
(a) 36
(b) 32
(c) 45
(d) 40
Ans: (b)
Sol: Let the efficiency of humans be 'E' and the efficiency of robots be ' R'.
In the first case
Total work done = (15E + 5R) x 30 …(i)
In the second case,
Total work done = (5E + 15R) x 60 …(ii)
Since same work is finished in both the cases, so by equating (i) and (ii), we have :
► (15E + 5R) x 30 = (5E + 15R) x 60
► (15E + 5R) = (5E + 15R) x 2
► or, 15E + 5R = 10E + 30R
► or, 5E = 25R
► or, E = 5R
Putting this value of E in (I), we have
Total work = (15E + 5R) x 30 = (15E + R) x 30 = 480E
Time taken by 15 humans = 480E / 15E days = 32 days.
Q3: When they work alone, B needs 25% more time to finish a job than A does. The two finish the job in 13 days in the following manner : A works alone till half the job is done, then A and B work together for four days, and finally B works alone to complete the remaining 5% of the job. In how many days can B alone finish the entire job? [2018]
(a) 20
(b) 16
(c) 22
(d) 18
Ans: (a)
Sol: Let the work completed by A in a day be 'a' units and that by B be 'b' units.
As per question :A alone works till half the work is completed. Thus, 50% of work is done and rest 50% needs to be completed.
Afterwards, A and B work together for 4 days and B works alone to complete the remaining 5% of the work. This means A and B in 4 days can complete 45% of the work.
Now suppose that the total amount of work to be done is 100 units.
► So, 4 a + 4b = 45 …(i)
Because B needs 25% more time than A to finish a job.
► So, 1.25 x b = a …(ii)
Substituting value of a from (ii) in (i), we get
► 5b + 4b = 45
► or, 9b = 45
► or, b = 5 units/day
Hence, B alone can finish the job in 100 / 5 = 20 days.
Q4: A tank is emptied everyday at a fixed time point, Immediately thereafter, either pump A or pump B or both start working until the tank is full. On Monday, A alone completed filling the tank at 8 pm. On Tuesday, B alone completed filling the tank at 6 pm. On Wednesday, A alone worked till 5 pm, and then B worked alone from 5 pm to 7 pm, to fill the tank. At what time was the tank filled on Thursday if both pumps were used simultaneously all along? [2018]
(a) 4 : 36 pm
(b) 4 : 12 pm
(c) 4 : 24 pm
(d) 4 : 48 pm
Ans: (c)
Sol: Let the tank be emptied everyday at 'T' pm. Let 'a' litres/hr' and 'b' litres/hr be the amount of water filled by pump A and pump B, respectively.
As per question, on Monday, A alone completed filling the tank at 8 pm. Therefore, the pump A worked for (8 - T ) hours.
So, the volume of the tank = a x (8 - T) litres.
Similarly, on Tuesday, B alone completed filling the tank at 6 pm.
Therefore, the pump B worked for (6 - T) hours.
Hence, the volume of the tank = b x (6 - T) litres.
On Wednesday, A alone worked till 5 pm. and then B worked alone from 5 pm to 7 pm, to fill the tank.
This means pump A worked for (5 - T) hours and pump B worked for rest of the 2 hours. Hence, the volume of the tank = a x (5 - t) + (2 x b) litres.
We can say that a x (8 - T) = b x (6 - T) = a x (5 - T) + 2b …(i)
or, a x (8 - T) = a x (5 - T) + 2b
or, 3a = 2b…(ii)
Again from (i) a x (8 - T) = b x (6 - T)
From (ii) we know that 3a = 2b
So, a x (8 -T) = (3a / 2) x (6 - T)
or, T = 2
Thus, the tank gets emptied at 2 pm daily.
A alone fills the tank at 8pm, thus, A takes 6 hours and pump B alone fills the tank at 6pm thus B takes 4 hours.
Hence, working together, both can fill the tank in (6 x 4 ) / (6 + 4 ) = 2.4 hours or 2 hours and 24 minutes.
Q5: A water tank has inlets of two types A and B. All inlets of type A when open, bring in water at the same rate. All inlets of type B, when open, bring in water at the same rate. The empty tank is completely filled in 30 minutes if 10 inlets of type A and 45 inlets of type B are open, and in 1 hour if 8 inlets of type A and 18 inlets of type B are open. In how many minutes will the empty tank get completely filled if 7 inlets of type A and 27 inlets of type B are open? [2018]
(a) 46 mins
(b) 48 mins
(c) 50 mins
(d) 52 mins
Ans: (b)
Sol: Let the rate at which each inlet of type A brings water be 'a' litres per minute and from B 'b' litres per minute.
Then, as per question 30 x (10a + 45b)
= 60 x (8a + 18b)
or, 300a + 450b = 480a + 1080b
or, 180a = 630b
or, 6a = 9b, Thus, a : b = 3 : 2 or b = (2 / 3)a …(i)
Total capacity of tank = 30 x (10a + 45b) = 30[10a + 45 x (2 / 3)a ] = 1200a
When 7 inlets of type A and 27 inlets of type B are open, the total efficiency
= 7a + 27b
= 7a + 27 x (2 / 3) a = 25a
So, time taken = capacity of tank/total efficiency = 1200a / 25a = 48 minutes
Hence, 48 min is the correct answer.
Q6: Ramesh and Ganesh can together complete a work in 16 days. After seven days of working together, Ramesh got sick and his efficiency fell by 30%. As a result, they completed the work in 17 days instead of 16 days. If Ganesh had worked alone after Ramesh got sick, in how many days would he have completed the remaining work? [2018]
(a) 13.5
(b) 11
(c) 12
(d) 14.5
Ans: (a)
Sol: Let the efficiency of Ramesh be R units per day and that of Ganesh be G units per day.
As per question 16 (R + G) = 17G + 7R + (R - 0.3R) x 10
16R + 16G = 17G + 7R + 7R
So, G = 2R, So total efficiency when both work together = R + G = R + 2R = 3R
Hence, total work = 16 x 3R = 48R
In second case, where Ramesh got sick after 7 days
Work left after 7 days = 48R - 7 (3R) = 27R
Time Ganesh would take to complete this work alone = 27R / 2R = 13.5 days.
2017
Q1: A person can complete a job in 120 days. He works alone on Day 1. On Day 2, he is joined by another person who also can complete the job in exactly 120 days. On Day 3, they are joined by another person of equal efficiency. Like this, everyday a new person with the same efficiency joins the work. How many days are required to complete the job? [2017]
(a) 15 days
(b) 16 days
(c) 17 days
(d) 19 days
Ans: (a)
Sol: Let the rate of work of a person by Y units/day.
Hence, the total work = 120Y.
Given : On first day, only one person works, on the second day two people work and so on.
Hence, the work done on day 1, day 2,… will be Y ,2Y ,3Y …respectively.
Let the total number of days required to complete the work is n.
Thus sum should be equal to 120Y.
So, Y + 2Y + 3Y +…+ nY = 120Y
or, 120Y = Y x n (n +1) / 2
or, n2 + n - 240 = 0 or (n - 15)(n + 16) = 0
So, n = 15 or n = -16
But, n = 15 is the only positive value.
Hence, it will take 15 days to complete the work.
Q2: A tank has an inlet pipe and an outlet pipe. If the outlet pipe is closed, then the inlet pipe fills the empty tank in 8 hours. If the outlet pipe is open, then the inlet pipe fills the empty tank in 10 hours. If only the outlet pipe is open, then in how many hours the full tank becomes half-full? [2017]
(a) 20
(b) 30
(c) 40
(d) 45
Ans: (a)
Sol: Let the time taken by the outlet pipe to empty the tank fully when only outlet pipe is open = T hours.
Then, as per question [(1 / 8) - (1 / T )] = 1 /10
or, 1 / T = 1 / 8 - 1 /10 = 1 / 40,
therefore the outlet pipe can empty the tank fully in 40 hours.
Hence, time taken by the outlet pipe to make the tank half-full = 40 / 2 = 20 hours.
Q3: Amal can complete a job in 10 days and Bimal can complete it in 8 days. Amal, Bimal and Kamal together complete the job in 4 days and are paid a total amount of Rs. 1000 as remuneration. If this amount is shared by them in proportion to their work, then Kamal's share, in rupees, is [2017]
(a) 100
(b) 200
(c) 300
(d) 400
Ans: (a)
Sol: Amal, Bimal and Kamla can together complete the job in 4 days.
Amal's contribution in 1 day =1 / 10 and Bimal's contribution = 1 / 8.
So Kamal's contribution = 1 / 4 - (1 / 8 + 1 / 10) = 1 / 40
Ratio of their work
= 1 / 10 : 1 / 8 : 1 / 40 = 4 : 5 : 1
So, amount of share for Kamal = 1000 x 1 /10 = ₹ 100
Q4: A person can complete a job in 120 days. He works alone on Day 1. On Day 2, he is joined by another person who also can complete the job in exactly 120 days. On Day 3, they are joined by another person of equal efficiency. Like this, everyday a new person with the same efficiency joins the work. How many days are required to complete the job? [2017]
(a) 15 days
(b) 17 days
(c) 16 days
(d) 18 days
Ans: (a)
Sol: Let the rate of work of a person by Y units/day.
Hence, the total work = 120Y .
Given : On first day, only one person works, on the second day two people work and so on.
Hence, the work done on day 1, day 2,… will be Y ,2Y ,3Y …respectively.
Let the total number of days required to complete the work is n.
Thus sum should be equal to 120Y.
So, Y + 2Y + 3Y +…+ nY = 120Y
or, 120Y = Y x n (n - 1) / 2
or, n2 + n - 240 = 0 or (n - 15)(n + 16) = 0
So, n = 15 or n = -16
But, n = 15 is the only positive value.
Hence, it will take 15 days to complete the work.
Q5: Four two-way pipes, A,B,C and D can either fill an empty tank or drain the full tank in 4, 10, 12 and 20 minutes, respectively. All four pipes were opened simultaneously when the tank is empty. Under which of the following conditions, the tank would be half filled after 30 minutes? [2017]
(a) Pipe A filled and pipes, B,C and D drained
(b) Pipe A drained and pipes B,C and D filled
(c) Pipes A and D drained and pipes B and C filled
(d) Pipes A and D filled and pipes B and C drained
Ans: (a)
Sol: Let the capacity of the tank
► = LCM (4 ,10,12,20) = 60
So, work done by A, B, C =15, 6, 5, 3 respectively.
Option 1 : Work Done in a minute
►= 15 - 6 - 5 - 3 = 1
So, after 30 minutes, the tank will be half filled.
2016
Q1: A water tank has M inlet pipes and N outlet pipes. An inlet pipe can fill the tank in 8 hours while an outlet pipe can empty the full tank in 12 hours. If all pipes are left open simultaneously, it takes 6 hours to fill the empty tank. What is the relationship between M and N? [2016]
(a) M : N = 1 : 1
(b) M : N = 2 : 1
(c) M : N = 2 : 3
(d) M : N = 3 : 2
(e) None of the above
Ans: (a)
Sol: As per question, M inlet pipes can fill the M / 8th part of the tank in 1 hour and N outlet pipes can empty N / 12th part of the tank in 1 hour.
If all pipes are left open, in 1 hour, the tank will be filled = M / 8 - N /12 = 1 / 6 (as the tank will take 6 hours to fill).
Then, 6 M - 4 N = 8, or, M = (8 + 4 N ) / 6.
There will be infinite number of solutions ( N = 1,4 ,7,10,13,16 ...) but none of the above ratios are correct.
For example, above equation is solvable when M = 2,N = 1 or M = 4, N = 4.
But the ratios 2 : 1 (i.e., M = 2,N = 1 ) or 1 : 1 ( M = 4, N = 4 ) are not correct because the solution of the above equation will not be an integer for values like M = 4 ,N = 2 or M = 6, N = 6.
Q2: In the marketing management course of an MBA programme, you and your roommate can complete an assignment in 30 days. If you are twice as efficient as your roommate, the time required by each to complete the assignment individually is [2016]
(a) 45 days and 90 days
(b) 30 days and 60 days
(c) 40 days and 120 days
(d) 45 days and 135 days
Ans: (a)
Sol: Let your efficiency of doing some work be t days, then the efficiency of your roommate is 2t days.
So, we have,
t = 45 days thus, 2t = 90 days
2015
Q1: Three pipes are connected to an inverted cone, with its base at the top. Two inlet pipes, A and B, are connected to the top of the cone and can fill the empty cone in 8 hours and 12 hours, respectively. The outlet pipe C, connected to the bottom, can empty a filled cone in 4 hours. When the cone is completely filled with water, all three pipes are opened. Two of the three pipes remain open for 20 hours continuously and the third pipe remains open for a lesser time. As a result, the height of the water inside the cone comes down to 50%. Which of the following options would be possible? [2015]
(a) Pipe A was open for 19 hours
(b) Pipe A was open for 19 hours 30 minutes
(c) Pipe B was open for 19 hours 30 minutes
(d) Pipe C was open for 19 hours 50 minutes
(e) The situation is not possible
Ans: (c)
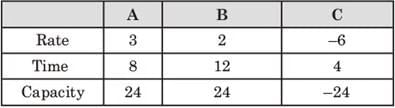
Sol: The two inlet A and B and one outlet pipe C, fill or empty the tank as per rates tabulated below :
Given : Two of the pipes are kept open for 20 hours and the third pipe C for a lesser period.
The tank is initially full and finally (volume = (1 / 3) x π x r2h) the water level drops to 1 / 2 and so the volume will become (1 / 3) x π x (r / 2)2 x h / 2 = 1 / 8 {(1 / 3) x π x r2h )}, i.e., 1 / 8th of the original volume.
This means 7 / 8th volume of water must have drained out.
From the table above, we can see that net rate of emptying the tank = 3 + 2 - 6 = 1 liter per hr.
So, to drain the full tank out, when all the pipes are open, it will take 24 hrs.
So, to drain 7 / 8th tank = 7 x 24 / 8 = 21 hrs.
Since, the 7 / 8th water drained out in 20 hrs only, so one of the two inlet pipes must have opened for lesser time. Assuming that if all the three pipes were open for all 20 hrs, we can see that 1 extra unit was required to be drained or the water was not filled by closing one of the inlet pipes a little early.
From the table, we can see that pipe B if opened for 1 / 2 hrs less, will fill the water by 1 litre less.
So, B works for 19.5 hrs only.
Q2: A tank is connected with both inlet pipes and outlet pipes. Individually, an inlet pipe can fill the tank in 7 hours and an outlet pipe can empty it in 5 hours. If all the pipes are kept open, it takes exactly 7 hours for a completely filled-in tank to empty. If the total number of pipes connected to the tank is 11, how many of these are inlet pipes? [2015]
(a) 2
(b) 4
(c) 5
(d) 6
Ans: (d)
Sol: Let there be i and o inlet and outlet pipes respectively.
∴ i + o = 11…(i)
Assume that the capacity of the tank is 35 units.
So, inlet pipe fills 5 units and the outlet pipes empties 7 units of the tank in one hour.
The completely filled tank empties in 7 hours.
∴ 7o - 5i = 5…(ii)
So, now we solve the equations, and get i and o and i = 6.
Q3: Three carpenters P,Q and R are entrusted with office furniture work. P can do a job in 42 days. If Q is 26% more efficient than P, and R is 50% more efficient than Q, then Q and R together can finish the job in approximately: [2015]
(a) 11 days
(b) 13 days
(c) 15 days
(d) 17 days
Ans: (b)
Sol: Let P do x units of work in one day.
∴ so, total work = 42x
So, Q and R do 1.26x and (1.26 x 1.5 =)1.89x units of work in one day, respectively.
∴ Total work done by Q and R in one day = 1.26x + 1.89x = 3.15x
So, Q and R can finish the work in (42x / 3.15x ≈) 13 days.
|
167 videos|229 docs|95 tests
|
FAQs on Time & Work CAT Previous Year Questions with Answer PDF
| 1. How to solve time and work problems quickly? |  |
| 2. What is the formula for calculating work done? |  |
| 3. How to solve time and work problems involving multiple people working together? |  |
| 4. How to approach time and work problems with different work rates? |  |
| 5. Can time and work problems be solved using algebraic equations? |  |