Types of Matrices | Mathematics (Maths) Class 12 - JEE PDF Download
Matrix Types: Overview
The different types of matrices are:

Types of Matrices: Explanations
Row Matrix
A matrix having only one row is called a row matrix. Thus A = [aij]mxn is a row matrix if m = 1. So, a row matrix can be represented as A = [aij]1×n. It is called so because it has only one row and the order of a row matrix will hence be 1 × n. For example, A = [1 2 4 5] is row matrix of order 1 x 4. Another example of the row matrix is P = [ -4 -21 -17 ] which is of the order 1 × 3.
Column Matrix
A matrix having only one column is called a column matrix. Thus, A = [aij]mxn is a column matrix if n = 1. Thus, the value of for a column matrix will be 1. Hence, the order is m × 1.
An example of a column matrix is: 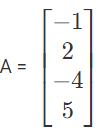 is column matrix of order 4 x 1.
is column matrix of order 4 x 1.
Just like the row matrices had only one row, column matrices have only one column. Thus, the value of for a column matrix will be 1. Hence, the order is m × 1. The general form of a column matrix is given by A = [aij]m×1. Other examples of a column matrix include: 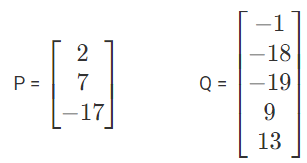
In the above example , P and Q are 3 ×1 and 5 × 1 order matrices respectively.
Zero or Null Matrix
If in a matrix all the elements are zero then it is called a zero matrix and it is generally denoted by 0. Thus, A =
[aij]mxn is a zero-matrix if aij = 0 for all i and j; E.g. 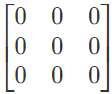 is a zero matrix of order 2 x 3.
is a zero matrix of order 2 x 3. 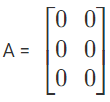
is a 3 x 2 null matrix & B = 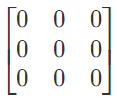 is 3 x 3 null matrix.
is 3 x 3 null matrix.
Singleton Matrix
If in a matrix there is only element then it is called singleton matrix. Thus, A = [aij]mxn is a singleton matrix if m = n = 1. E.g. [2], [3], [a], [] are singleton matrices.
Horizontal Matrix
A matrix of order m x n is a horizontal matrix if n > m; E.g.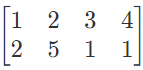
Vertical Matrix
A matrix of order m x n is a vertical matrix if m > n; E.g. 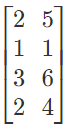
Square Matrix
If the number of rows and the number of columns in a matrix are equal, then it is called a square matrix.
Thus, A = [aij]mxn is a square matrix if m = n; E.g. 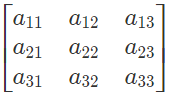
is a square matrix of order 3 × 3.
The sum of the diagonal elements in a square matrix A is called the trace of matrix A, and which is denoted by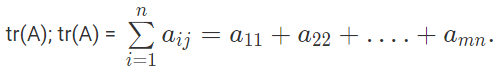
Another example of a square matrix is: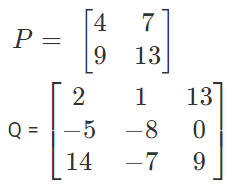
The order of P and Q is 2 × 2 and 3 × 3 respectively.
Diagonal Matrix
If all the elements, except the principal diagonal, in a square matrix, are zero, it is called a diagonal matrix. Thus, a square matrix A = [aij] is a diagonal matrix if aij = 0,when i ≠ j; E.g. 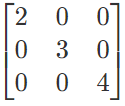
is a diagonal matrix of order 3 x 3, which can also be denoted by diagonal [2 3 4]. The special thing is, all the non-diagonal elements of this matrix are zero. That means only the diagonal has non-zero elements. There are two important things to note here which are
(i) A diagonal matrix is always a square matrix
(ii) The diagonal elements are characterized by this general form: aij where i = j. This means that a matrix can have only one diagonal.
Few more example of diagonal matrix are:
P = [9]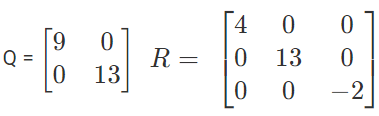
In the above examples, P, Q, and R are diagonal matrices with order 1 × 1, 2 × 2 and 3 × 3 respectively. When all the diagonal elements of a diagonal matrix are the same, it goes by a different name- scalar matrix which is discussed below.
Scalar Matrix
If all the elements in the diagonal of a diagonal matrix are equal, it is called a scalar matrix. Thus, a square matrix A = [aij]mx is a scalar matrix if aij =  where k is a constant.
where k is a constant. 
is a scalar Matrix.
More examples of scalar matrix are: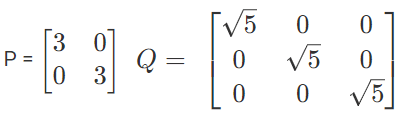
Now, what if all the diagonal elements are equal to 1? That will still be a scalar matrix and obviously a diagonal matrix. It has got a special name which is known as the identity matrix.
Unit Matrix or Identity Matrix
If all the elements of a principal diagonal in a diagonal matrix are 1, then it is called a unit matrix. A unit matrix of order n is denoted by In. Thus, a square matrix A = [aij]m×n is an identity matrix if 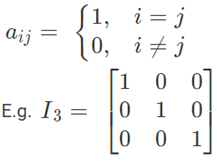
Conclusions:
- All identity matrices are scalar matrices
- All scalar matrices are diagonal matrices
- All diagonal matrices are square matrices
It should be noted that the converse of the above statements is not true for any of the cases.
Equal Matrices
Equal matrices are those matrices which are equal in terms of their elements. The conditions for matrix equality are discussed below.
Equality of Matrices Conditions
Two matrices A and B are said to be equal if they are of the same order and their corresponding elements are equal, i.e. Two matrices A = [aij]m×n and B = [bij]r×s are equal if:
(a) m = r i.e. the number of rows in A = the number of rows in B.
(b) n = s, i.e. the number of columns in A = the number of columns in B
(c) aij = bij, for i = 1, 2, ….., m and j = 1, 2, ….., n, i.e. the corresponding elements are equal;
For example, Matrices 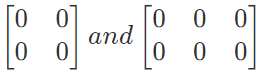 are not equal because their orders are not the same.
are not equal because their orders are not the same.
But, If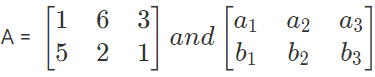 are equal matrices then,
are equal matrices then,
a1 = 1, a2 = 6, a3 = 3, b1 = 5, b2 = 2, b3 = 1.
Triangular Matrix
A square matrix is said to be a triangular matrix if the elements above or below the principal diagonal are zero. There are two types:
Upper Triangular Matrix
A square matrix [aij] is called an upper triangular matrix, if aij = 0, when i > j.  is an upper uriangular matrix of order 3 x 3.
is an upper uriangular matrix of order 3 x 3.
Lower Triangular Matrix
A square matrix is called a lower triangular matrix, if aij = 0 when i < j. 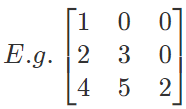 is a lower triangular matrix of order 3 x 3.
is a lower triangular matrix of order 3 x 3.
Singular Matrix and Non-Singular Matrix
Matrix A is said to be a singular matrix if its determinant |A| = 0, otherwise a non-singular matrix, i.e. If for det |A| = 0, it is singular matrix and for det |A| ≠ 0, it is non-singular.
Symmetric and Skew Symmetric Matrices
- Symmetric matrix: A square matrix A = [aij] is called a symmetric matrix if aij = aji, for all i,j values;
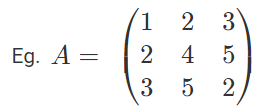 is symmetric, because a12 = 2 = a21, a31 = 3 = a13 etc.
is symmetric, because a12 = 2 = a21, a31 = 3 = a13 etc.
Note: A is symmetric if A’ = A (where ‘A’ is the transpose of matrix)
- Skew-Symmetric Matrix: A square matrix A = [aij] is a skew-symmetric matrix if aij = aji, for all values of i,j. [putting j = i] aii = 0
Thus, in a skew-symmetric matrix all diagonal elements are zero; E.g.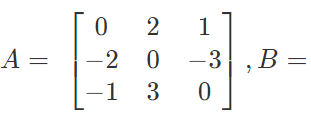
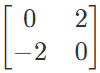
are skew-symmetric matrices.
Note: A square matrix A is a skew-symmetric matrix A’ = -A.
Some important Conclusions on Symmetric and Skew-Symmetric Matrices:
- If A is any square matrix, then A + A’ is a symmetric matrix and A – A’ is a skew-symmetric matrix.
- Every square matrix can be uniquely expressed as the sum of a symmetric matrix and a skew-symmetric matrix. A = 1/2 (A + A') + 1/2 (A - A') = 1/2 (B + C), where B is symmetric and C is a skew symmetric matrix.
- If a and B are symmetric matrices, then AB is symmetric AB = BA, i.e. A & B commute.
- The matrix B’AB is symmetric or skew-symmetric in correspondence if A is symmetric or skew-symmetric.
- All positive integral powers of a symmetric matrix are symmetric.
- Positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
Hermitian and Skew-Hermitian Matrices
A square matrix A = [aij] is said to be a Hermitian matrix if aij 
 are Hermitian matrices
are Hermitian matrices
Important Notes:
- If A is a Hermitian matrix then
 thus every diagonal element of a Hermitian Matrix must be real.
thus every diagonal element of a Hermitian Matrix must be real. - If a Hermitian matrix over the set of real numbers is actually a real symmetric matrix; and A a square matrix,
A = [aij] is said to be a skew-Hermitian if 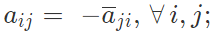 i.e. Aθ = – A;
i.e. Aθ = – A; 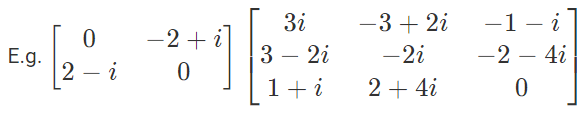
are skew-Hermitin matrices.
- If A is a skew-Hermitian matrix then =\frac{1}{2}(A+A’)+\frac{1}{2}(A-A’)=\frac{1}{2}(B+C),
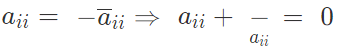
i.e. aii must be purely imaginary or zero.
- A skew-Hermitian matrix over the set of real numbers is actually is a real skew-symmetric matrix.
Special Matrices
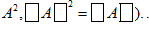
(a) Idempotent Matrix: A square matrix is idempotent, provided A2 = A. For an idempotent matrix 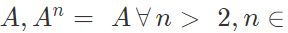
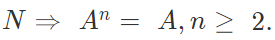
For an idempotent matrix A, det A = 0 or x.
(b) Nilpotent Matrix: A nilpotent matrix is said to be nilpotent of index p, (p ∈ N), if Ap = O, Ap - 1 ≠ O, i.e. if p is the least positive integer for which Ap = O, then A is said to be nilpotent of index p.
(c) Periodic Matrix:
A square matrix which satisfies the relation Ak + 1 = A, for some positive integer K, then A is periodic with period K, i.e. if K is the least positive integer for which Ak + 1 = A, nd A is said to be periodic with period K. If K =1 then A is called idempotent.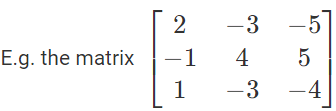
has the period 1.
Notes:
(i) Period of a square null matrix is not defined.
(ii) Period of an idempotent matrix is 1.
(d) Involutary Matrix:
If A2 = I, the matrix is said to be an involutary matrix. An involutary matrix its own inverse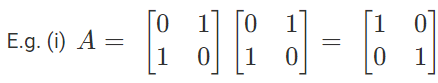
|
223 videos|377 docs|167 tests
|
FAQs on Types of Matrices - Mathematics (Maths) Class 12 - JEE
| 1. What is a matrix? |  |
| 2. What are the different types of matrices? |  |
| 3. What is the significance of a square matrix? |  |
| 4. How is an identity matrix useful in matrix operations? |  |
| 5. How can symmetric matrices be utilized in real-world applications? |  |





















