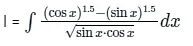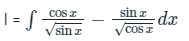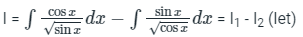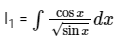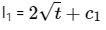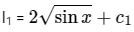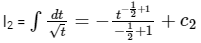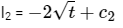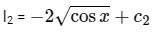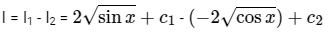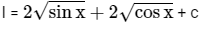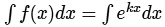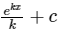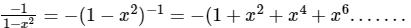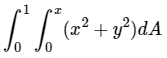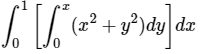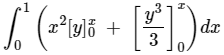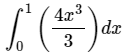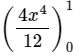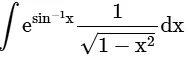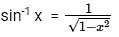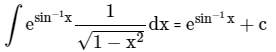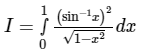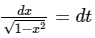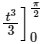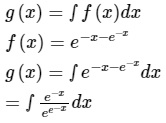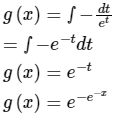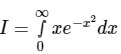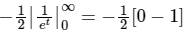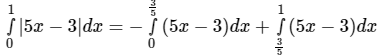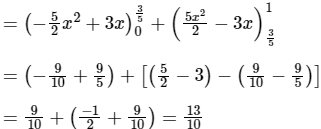JEE Advanced (Single Correct Type): Indefinite Integral | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q.1. What is 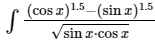 equal to?
(a)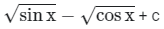
(b)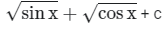
(c)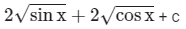
(d)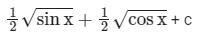

Correct Answer is option (c)
Given,

⇒
⇒
Computing I₁,

Put sin x = t → cos x dx = dt
⇒
⇒
⇒
Similarly,

Put cos x = t → - sin x dx = dt
⇒
⇒
⇒
Putting these value in I,
⇒
⇒
∴ The correct answer is option (C).

Q.2. If (x) = e^kx; then find the indefinite integral of f (x)?
(a)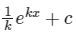
(b) e^x + c
(c) -e^-x + c
(d)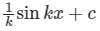

Correct Answer is option (a)
Integration of e^kx
Integrating f (x) = e^kx with respect to dx.

=
where 'c' is the constant,

Q.3. 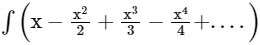dx is equal to
(a)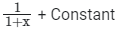
(b)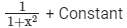
(c)
(d)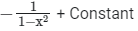

Correct Answer is option (c)
The Given Question is Wrong, Marks are allotted to all.
Given that,

option 1-

option 2-

option 3-

option 4-

Q.4. The value of 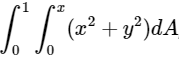, where dA indicate small area in xy-plane, is
(a) 1/2 sq. units
(b) 1/3 sq. units
(c) -1/2 sq. units
(d) -1/3 sq. units

Correct Answer is option (b)
Given:






= 1/3

Q.5. Evaluate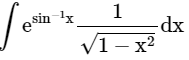
(a) e^sinx + c
(b) 2e^sin-1x + c
(c) e^sin-1x + c
(d) e^sin-1x + 2c

Correct Answer is option (c)
Given Integral

Let,  as we know the derivative of
Now the equation reduces to
 ⇒ we know ∫e^xdx = e^x + c  
∴ ∫ etdt = et + c, as t = sin-1 x our equation becomes e^sin-1x  + c 
∴

Q.6. Consider the following definite integral: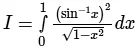

The value of the integral is
(a) π³/24
(b) π³/12
(c) π³/48
(d) π³/64

Correct Answer is option (a)

Put sin^-1 x = t 

=
=
= π³/24

Q.7. Let x be a continuous variable defined over the interval (-∞, ∞) and  . The integral g(x)=∫f(x)dx  is equal to 
(a)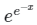
(b)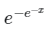
(c)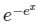
(d) e^-x

Correct Answer is option (b)

Substitude e^-x = t 
-e^-x dx = dt 

Q.8.  =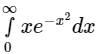
(a) 1/3
(b) 1/2
(c) -1/2
(d) -1/3

Correct Answer is option (b)

Let, t = x² ⇒ dt = 2xdx ⇒ xdx = dt/2 

=
I = 1/2

Q.9. The value of 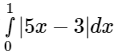 is
(a) -1/2
(b) 13/10
(c) 1/2
(d) 28/10

Correct Answer is option (b)
For Integration with modulus, first we have to find the point where the sign of the value of the function gets change.
Given:

f(x) = 5x - 3 = 0
x = 3/5
∴ from 0 to 3/5 the function is negative and 3/5 to 1 the function is positive.

Q.10. 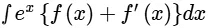 is equal to
(a)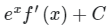
(b)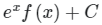
(c)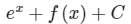
(d) None of these

Correct Answer is option (b)
Let,
I = ∫ex{f(x)  +f′(x)}dx
= ∫ex f(x)dx + ∫ex f′(x)dx + C
By solving through integration by parts, we get
= {ex f(x) − ∫f′(x)ex dx} + ∫ex f′(x)dx + C
= f(x).ex + C
where C is constant