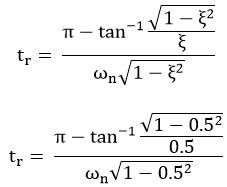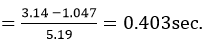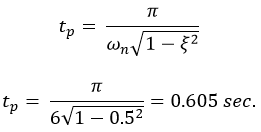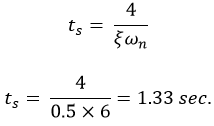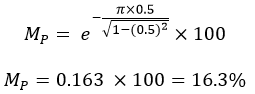Time Response of Second Order System | Control Systems - Electrical Engineering (EE) PDF Download
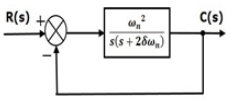
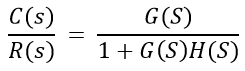
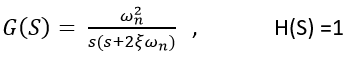
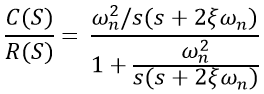
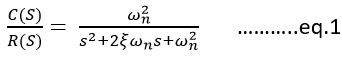
In the above transfer function, the power of 's' is two in the denominator. That is why the above transfer function is of a second order, and the system is said to be the second order system.
Time response of second order system with unit step
From equation 1
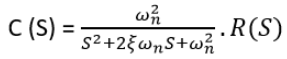
For unit step the input is
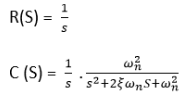
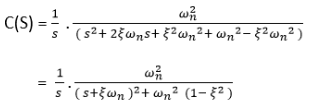
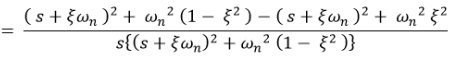
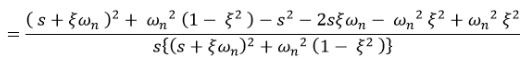

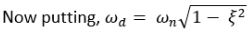
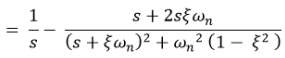
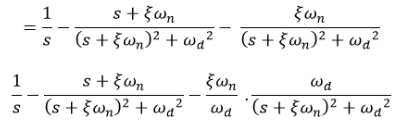
Now taking the inverse Laplace of above equation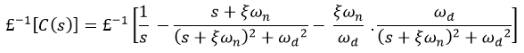
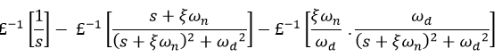
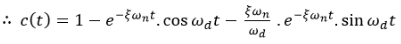
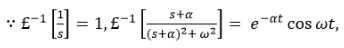
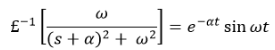
This equation can also be written as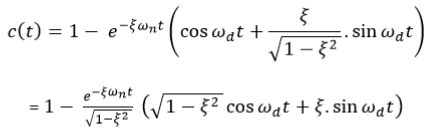
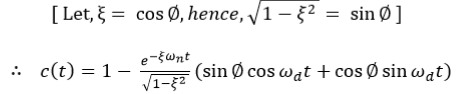
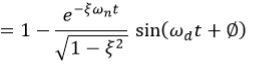
The error signal is given by e(t) = r(t) - c(t), and hence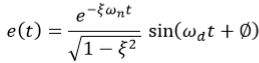
Transient response specification of second order system
The performance of the control system are expressed in terms of transient response to a unit step input because it is easy to generate initial condition basically are zero.
Following are the common transient response characteristics:
- Delay Time.
- Rise Time.
- Peak Time.
- Maximum Peak.
- Settling Time.
- Steady State error.
- Delay Time
The time required for the response to reach 50% of the final value in the first time is called the delay time.
Rise Time
The time required for response to rising from 10% to 90% of final value, for an overdamped system and 0 to 100% for an underdamped system is called the rise time of the system.
Peak Time
The time required for the response to reach the 1st peak of the time response or 1st peak overshoot is called the Peak time.
Maximum overshoot
The difference between the peak of 1st time and steady output is called the maximum overshoot. It is defined by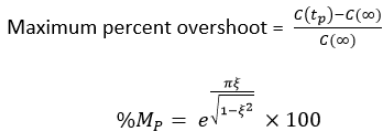
Settling Time (ts)
The time that is required for the response to reach and stay within the specified range (2% to 5%) of its final value is called the settling time.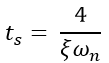
Steady State Error (ess)
The difference between actual output and desired output as time't' tends to infinity is called the steady state error of the system.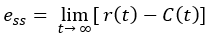
Example
When a second-order system is subjected to a unit step input, the values of ξ = 0.5 and ωn = 6 rad/sec. Determine the rise time, peak time, settling time and peak overshoot.
Given-
ξ = 0.5 ω n = 6 rad/sec
Peak Time:
Settling Time:Maximum overshoot:
|
53 videos|107 docs|40 tests
|
FAQs on Time Response of Second Order System - Control Systems - Electrical Engineering (EE)
| 1. What is a second order system? |  |
| 2. How is the time response of a second order system defined? |  |
| 3. What are the characteristics of the time response of a second order system? |  |
| 4. How is the damping ratio of a second order system related to its time response? |  |
| 5. What are the applications of second order systems in real life? |  |