JEE Exam > JEE Notes > Study Plan for JEE > 3 Days Timetable: Vectors (2025)
3 Days Timetable: Vectors (2025) | Study Plan for JEE PDF Download
Vectors are not just another topic in Physics—they are the foundation of Mechanics, Electromagnetism, and even Modern Physics. Without a strong grasp of vectors, solving force equations, understanding angular momentum, and analyzing electromagnetic fields becomes significantly more challenging. This is why JEE aspirants must master vectors to build a solid conceptual base for the rest of Physics.
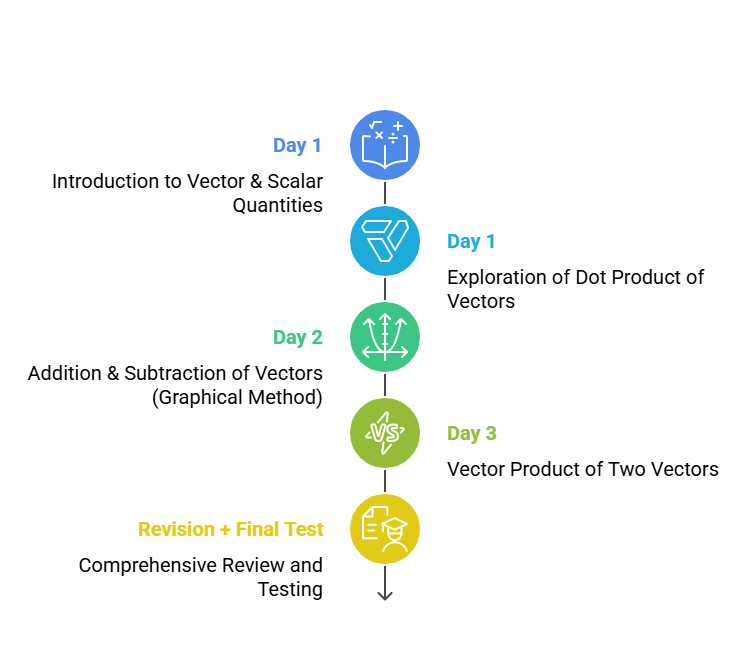3 Day Study Plan
Importance of Vectors in Physics
On average, 15-20% of Mechanics problems require direct application of vector operations.
Graphical vector problems (addition, subtraction, parallelogram law) frequently appear in JEE Mains.
Vector dot & cross products are widely tested in JEE Advanced, especially in Torque, Angular Momentum, and Work-Energy Theorem problems.
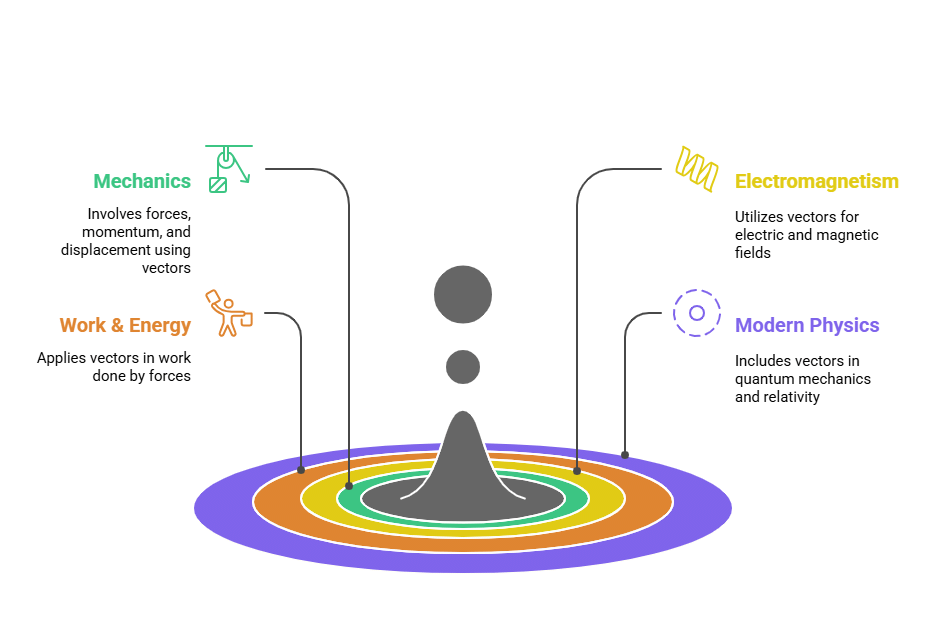Vectors in Physics
Day 1: Vector & Scalar Quantities, Dot Product of Vectors
- You can start by reading the chapter notes on Vector & Scalar Quantities available on EduRev.
- After that, watch video tutorials & read chapter notes on Dot Product of Vectors for a deeper understanding.
- Now, you are ready to apply & practice and solve NCERT Back Exercises and try problems from HC Verma & DC Pandey.
Challenge yourself: Can you explain Dot Product in 2 mins to a friend?
Day 2: Addition & Subtraction of Vectors (Graphical Method)
- Start your day with reading the chapter notes on Addition & Subtraction of Vectors using the graphical method, available on EduRev.
- Additionally, you can watch video on above topic.
Play: Can you explain vector addition in a minute!
Day 3: Vector Product of Two Vectors
- You can start by reading the chapter notes on Vector Product of Two Vectors available on EduRev.
- Then, can watch video tutorials to understand the concept thoroughly.
- Start solving practice problems from DC Pandey, HC Verma, and Irodov on this topic.
Revision + Final Test
- First, revise notes, and then go through the Flashcards.
- Then, try to solve Solved Examples of vectors & Previous Year JEE Questions Doc available on EduRev.
- After that, try to attempt the tests available topicwise such as cross product of two vectors, scalar product etc. and also full chapter test available on EduRev.
Here are some links for practice:
Practice Materials:
Additional Resources:
- How to prepare for JEE Mains and advanced
- How to Prepare for JEE Physics
- Basic Mathematics for Physics
Good luck with your preparation!
The document 3 Days Timetable: Vectors (2025) | Study Plan for JEE is a part of the JEE Course Study Plan for JEE.
All you need of JEE at this link: JEE
FAQs on 3 Days Timetable: Vectors (2025) - Study Plan for JEE
| 1. What are vector and scalar quantities, and how do they differ? |  |
Ans.Vector quantities have both magnitude and direction (e.g., velocity, force), while scalar quantities have only magnitude (e.g., mass, temperature). Understanding this distinction is crucial in physics as it affects how we perform calculations and analyze physical situations.
| 2. How do you calculate the dot product of two vectors, and what does it represent? | |
Ans.The dot product of two vectors A and B is calculated as A·B = |A| |B| cos(θ), where θ is the angle between the two vectors. The dot product represents the extent to which two vectors act in the same direction and is useful in determining work done when a force acts along a displacement.
| 3. What is the graphical method for adding and subtracting vectors? | |
Ans.The graphical method involves drawing vectors to scale on a graph, using arrows to represent direction and length for magnitude. To add vectors, place the tail of the second vector at the head of the first and draw the resultant vector from the tail of the first to the head of the second. For subtraction, reverse the direction of the vector to be subtracted and then add it as above.
| 4. What is the vector product of two vectors, and when is it used? | |
Ans.The vector product, or cross product, of two vectors A and B is given by A × B = |A| |B| sin(θ) n, where θ is the angle between the vectors and n is the unit vector perpendicular to the plane containing A and B. It is used primarily in physics to find quantities such as torque and angular momentum, which depend on direction.
| 5. How can I prepare effectively for the vectors section in the JEE exam? | |
Ans.Effective preparation for the vectors section in the JEE exam includes mastering the fundamental concepts of vector and scalar quantities, practicing problems on dot and cross products, and applying graphical methods for vector addition and subtraction. Regular revision and taking mock tests can also enhance problem-solving speed and accuracy.
Related Exams
About this Document
1.7K Views
4.71/5
Rating
May 19, 2025
Last updated
Document Description: 3 Days Timetable: Vectors (2025) for JEE 2025 is part of Study Plan for JEE preparation.
The notes and questions for 3 Days Timetable: Vectors (2025) have been prepared according to the JEE exam syllabus. Information about 3 Days Timetable: Vectors (2025) covers topics
like Importance of Vectors in Physics, Day 1: Vector & Scalar Quantities, Dot Product of Vectors, Day 2: Addition & Subtraction of Vectors (Graphical Method), Day 3: Vector Product of Two Vectors, Revision + Final Test and 3 Days Timetable: Vectors (2025) Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for 3 Days Timetable: Vectors (2025).
Introduction of 3 Days Timetable: Vectors (2025) in English is available as part of our Study Plan for JEE
for JEE & 3 Days Timetable: Vectors (2025) in Hindi for Study Plan for JEE course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: 3 Days Timetable: Vectors (2025) | Study Plan for JEE
Description
Full syllabus notes, lecture & questions for 3 Days Timetable: Vectors (2025) | Study Plan for JEE - JEE | Plus excerises question with solution to help you revise complete syllabus for Study Plan for JEE | Best notes, free PDF download
Information about 3 Days Timetable: Vectors (2025)
In this doc you can find the meaning of 3 Days Timetable: Vectors (2025) defined & explained in the simplest way possible. Besides explaining types of
3 Days Timetable: Vectors (2025) theory, EduRev gives you an ample number of questions to practice 3 Days Timetable: Vectors (2025) tests, examples and also practice JEE
tests
Related Searches
study material
,past year papers
,shortcuts and tricks
,3 Days Timetable: Vectors (2025) | Study Plan for JEE
,mock tests for examination
,practice quizzes
,Objective type Questions
,3 Days Timetable: Vectors (2025) | Study Plan for JEE
,Previous Year Questions with Solutions
,Sample Paper
,video lectures
,Viva Questions
,3 Days Timetable: Vectors (2025) | Study Plan for JEE
,Summary
,Important questions
,Extra Questions
,Exam
,Semester Notes
,ppt
,MCQs
,Free
;
Additional Information about 3 Days Timetable: Vectors (2025) for JEE Preparation
3 Days Timetable: Vectors (2025) Free PDF Download
The 3 Days Timetable: Vectors (2025) is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the 3 Days Timetable: Vectors (2025) now and kickstart your journey towards success in the JEE exam.
Importance of 3 Days Timetable: Vectors (2025)
The importance of 3 Days Timetable: Vectors (2025) cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
3 Days Timetable: Vectors (2025) Notes
3 Days Timetable: Vectors (2025) Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to 3 Days Timetable: Vectors (2025).
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, 3 Days Timetable: Vectors (2025) Notes on EduRev are your ultimate resource for success.
3 Days Timetable: Vectors (2025) JEE Questions
The "3 Days Timetable: Vectors (2025) JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study 3 Days Timetable: Vectors (2025) on the App
Students of JEE can study 3 Days Timetable: Vectors (2025) alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the 3 Days Timetable: Vectors (2025),
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of 3 Days Timetable: Vectors (2025) is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup