Bank Exams Exam > Bank Exams Notes > Quantitative Aptitude/संख्यात्मक योग्यता > चतुर्भुज: अवलोकन और उदाहरण
चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams PDF Download
कोई चार बिंदु जो एक ही रेखा पर नहीं होते, एक चतुर्भुज बनाते हैं; यह आकृति अपने रूप के अनुसार विभिन्न नामों से जानी जाती है। एक चतुर्भुज एक सपाट भूगणितीय आकृति है जिसमें चार भुजाएँ और चार कोने होते हैं। चतुर्भुजों को समझना SSC, रेल, AAI और शैक्षणिक परीक्षण जैसे विभिन्न परीक्षाओं के लिए आवश्यक है। एक चतुर्भुज में समांतर चतुर्भुज, आयत, वर्ग, समचतुर्भुज, ट्रेपेजियम और पतंग जैसी आकृतियाँ शामिल हैं, जिनकी अपनी विशेषताएँ और सूत्र होते हैं। ये भूगणितीय अवधारणाएँ प्रतियोगी परीक्षाओं और शैक्षणिक अध्ययन के लिए महत्वपूर्ण हैं।चतुर्भुज भूगणित में, चतुर्भुज एक आकृति है जिसमें चार भुजाएँ, चार कोण, और चार शीर्ष होते हैं। इसे चार बिंदुओं को जोड़कर बनाया जाता है जहाँ कोई तीन बिंदु एक सीधी रेखा में नहीं होते। कई प्रकार के चतुर्भुज मौजूद हैं, जिनमें वर्ग, आयत, समांतर चतुर्भुज, समचतुर्भुज, ट्रेपेजियम, और पतंग शामिल हैं। हम आगे के अनुभागों में प्रत्येक प्रकार का अन्वेषण करेंगे।चतुर्भुजों के प्रकार चतुर्भुज शब्द लैटिन शब्द से आया है, जहाँ Quadra का अर्थ है चार और Latus का अर्थ है भुजाएँ। एक चतुर्भुज में चार भुजाएँ हो सकती हैं जो समान या भिन्न हो सकती हैं। चतुर्भुजों के उदाहरणों में आयत, वर्ग, ट्रेपेज़ॉइड, और पतंग शामिल हैं, जो सामान्यतः चार भुजाओं की संरचना प्रदर्शित करते हैं। विभिन्न प्रकार के चतुर्भुजों के बारे में नीचे विस्तार से वर्णन किया गया है:
- समांतर चतुर्भुज
परिभाषा: एक चतुर्भुज जिसमें दो जोड़े विपरीत भुजाएँ समानांतर और लंबाई में समान होती हैं।
विशेषताएँ:
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत भुजाएँ लंबाई में समान हैं (AB = CD, BC = AD)।
- विकर्ण एक-दूसरे को परिभाजित करते हैं।
- किसी भी दो निकटवर्ती कोणों का योग 180 डिग्री है (∠A + ∠B = 180°, ∠B + ∠C = 180°, आदि)।
- आयत
परिभाषा: एक समांतर चतुर्भुज जहाँ प्रत्येक कोण 90 डिग्री मापता है।
विशेषताएँ:
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत भुजाएँ लंबाई में समान हैं (AB = CD, BC = AD)।
- सभी कोण 90 डिग्री के बराबर हैं (∠A = ∠B = ∠C = ∠D = 90°)।
- विकर्ण एक-दूसरे को परिभाजित करते हैं और लंबाई में समान होते हैं।
- वर्ग
परिभाषा: एक समांतर चतुर्भुज जिसमें सभी भुजाएँ समान और प्रत्येक कोण 90 डिग्री मापता है।
विशेषताएँ:
- सभी भुजाएँ लंबाई में समान हैं (AB = BC = CD = DA)।
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- सभी कोण 90 डिग्री के बराबर हैं (∠A = ∠B = ∠C = ∠D = 90°)।
- विकर्ण एक-दूसरे को दाहिने कोणों पर काटते हैं और लंबाई में समान होते हैं।
- समचतुर्भुज
परिभाषा: एक समांतर चतुर्भुज जिसमें सभी भुजाएँ समान होती हैं और विकर्ण एक-दूसरे को दाहिने कोणों पर काटते हैं।
विशेषताएँ:
- सभी भुजाएँ लंबाई में समान हैं (AB = BC = CD = DA)।
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत कोण समान होते हैं।
- विकर्ण एक-दूसरे को लंबवत रूप से परिभाजित करते हैं।
- ट्रेपेजियम
परिभाषा: एक चतुर्भुज जिसमें केवल एक जोड़ी विपरीत भुजाएँ समानांतर होती हैं।
विशेषताएँ:
- केवल एक जोड़ी विपरीत भुजाएँ समानांतर हैं (AB || CD)।
- गैर-समानांतर भुजाएँ ट्रेपेजियम के पैर कहलाती हैं।
- विकर्ण समान अनुपात में एक-दूसरे को परिभाजित नहीं करते हैं।
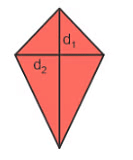
- पतंग
परिभाषा: एक चतुर्भुज जिसमें दो जोड़े निकटवर्ती भुजाएँ समान लंबाई में होती हैं।
विशेषताएँ:
- दो जोड़े निकटवर्ती भुजाएँ समान हैं (AB = AD, BC = CD)।
- विकर्ण दाहिने कोण पर मिलते हैं।
- एक विकर्ण दूसरे को परिभाजित करता है।
- चतुर्भुज का परिमाप
परिमाप का अर्थ है किसी सपाट आकृति के किनारे के चारों ओर की कुल दूरी।
चार भुजाओं वाली आकृति (चतुर्भुज) में, परिमाप सभी चार भुजाओं की लंबाई का योग होता है।
विभिन्न प्रकार के चतुर्भुजों के अलग-अलग परिमाप होते हैं।
नोट: परिमाप 2D आकृति, जैसे वर्ग या आयत के किनारे के चारों ओर की कुल दूरी है।
- चतुर्भुज का क्षेत्रफल
चार भुजाओं वाली आकृति का क्षेत्रफल कुल स्थान है जो यह घेरती है। यहाँ विभिन्न आकृतियों के लिए क्षेत्रफल के सूत्र हैं:
- वर्ग: सभी भुजाएँ समान हैं। क्षेत्रफल = भुजा × भुजा
- समांतर चतुर्भुज: विपरीत भुजाएँ समानांतर हैं। क्षेत्रफल = आधार × ऊँचाई
- आयत: विपरीत भुजाएँ समान और सभी कोण 90 डिग्री हैं। क्षेत्रफल = लंबाई × चौड़ाई
- समचतुर्भुज: सभी भुजाएँ समान हैं, विपरीत कोण समान हैं। क्षेत्रफल = (विकर्ण1 × विकर्ण2) / 2
- ट्रेपेजियम: एक जोड़ी समानांतर भुजाएँ। क्षेत्रफल = 0.5 × (समानांतर भुजाओं का योग) × ऊँचाई
- पतंग: दो जोड़े निकटवर्ती भुजाएँ समान हैं। क्षेत्रफल = 0.5 × (विकर्ण1 × विकर्ण2)
- समांतर चतुर्भुज: विपरीत भुजाएँ एक-दूसरे के समानांतर होती हैं और कोणों का योग 180 डिग्री होता है।
- आयत: सभी कोण 90 डिग्री के बराबर हैं और कोणों का योग 180 डिग्री होता है।
- वर्ग: सभी भुजाएँ समान लंबाई की होती हैं और सभी कोण 90 डिग्री के बराबर होते हैं।
- समचतुर्भुज: सभी भुजाएँ समान लंबाई की होती हैं और कोणों का योग 180 डिग्री होता है।
- ट्रेपेजियम: केवल एक जोड़ी भुजाएँ समानांतर होती हैं।
- चतुर्भुजों की चार भुजाएँ होती हैं।
- चतुर्भुजों के चार शीर्ष होते हैं।
- चतुर्भुजों के दो विकर्ण होते हैं।
- सभी आंतरिक कोणों का योग 360 डिग्री होता है।
- उदाहरण 1: चार भुजाओं वाली आकृति का परिमाप ज्ञात करें जिनकी लंबाई 6 सेमी, 7 सेमी, 8 सेमी और 13 सेमी है।
समाधान: दी गई जानकारी के अनुसार, चार भुजाओं की लंबाई 6 सेमी, 7 सेमी, 8 सेमी, और 13 सेमी है।
ज्ञात है कि परिमाप सभी चार भुजाओं की लंबाई का योग होगा।
P(परिमाप) = 6 सेमी + 7 सेमी + 8 सेमी + 13 सेमी = 34 सेमी
- उदाहरण 2: यदि एक पतंग के दो विकर्णों की लंबाई 22 सेमी और 6 सेमी है, तो उसका क्षेत्रफल क्या होगा?
समाधान: पतंग का क्षेत्रफल = 1/2 × विकर्ण1 × विकर्ण2 = 1/2 × 22 × 6
इसलिए, पतंग का क्षेत्रफल = 66 वर्ग मीटर।
- उदाहरण 3: उस समांतर चतुर्भुज का परिमाप ज्ञात करें जिसकी विपरीत भुजाएँ 13 सेमी और 6 सेमी हैं।
समाधान: समांतर चतुर्भुज के गुण के अनुसार, विपरीत भुजाएँ समान लंबाई की होती हैं।
परिमाप = 13 सेमी + 6 सेमी + 13 सेमी + 6 सेमी = 38 सेमी
- उदाहरण 4: एक आयत का आधार ज्ञात करें जिसका क्षेत्रफल 72 वर्ग इकाइयाँ है और ऊँचाई 8 इकाइयाँ है।
दी गई जानकारी: क्षेत्रफल = 72 वर्ग इकाइयाँ
ऊँचाई = 8 इकाइयाँ
आयत का क्षेत्रफल = आधार × ऊँचाई
72 = आधार × 8
आधार = 72/8 = 9 इकाइयाँ
चतुर्भुज के प्रकार
चतुर्भुज (Quadrilateral) शब्द लैटिन के एक शब्द से उत्पन्न हुआ है, जहाँ Quadra का अर्थ चार और Latus का अर्थ भुजाएँ हैं। एक चतुर्भुज के चार भुजाएँ हो सकती हैं जो समान या भिन्न हो सकती हैं। चतुर्भुज के उदाहरणों में आयत (rectangle), वर्ग (square), ट्रेपेजियम (trapezoid), और पतंग (kite) शामिल हैं, जो आमतौर पर चार भुजाओं की संरचना दिखाते हैं। चतुर्भुज के विभिन्न प्रकार निम्नलिखित हैं:
- पैरालेलोग्राम
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत भुजाएँ समान लंबाई की हैं (AB = CD, BC = AD)।
- आड़ा रेखाएँ एक-दूसरे को बिसेक्ट करती हैं।
- किसी भी दो सन्निकट कोणों का योग 180 डिग्री है (∠A + ∠B = 180°, ∠B + ∠C = 180°, आदि)।
- आयत
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत भुजाएँ समान लंबाई की हैं (AB = CD, BC = AD)।
- सभी कोण 90 डिग्री के बराबर हैं (∠A = ∠B = ∠C = ∠D = 90°)।
- आड़ा रेखाएँ एक-दूसरे को बिसेक्ट करती हैं और समान लंबाई की होती हैं।
- वर्ग
- सभी भुजाएँ समान लंबाई की हैं (AB = BC = CD = DA)।
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- सभी कोण 90 डिग्री के बराबर हैं (∠A = ∠B = ∠C = ∠D = 90°)।
- आड़ा रेखाएँ एक-दूसरे को बिसेक्ट करती हैं और समान लंबाई की होती हैं।
- रंबस
- सभी भुजाएँ समान लंबाई की हैं (AB = BC = CD = DA)।
- विपरीत भुजाएँ समानांतर हैं (AB || CD, BC || AD)।
- विपरीत कोण समान हैं।
- आड़ा रेखाएँ एक-दूसरे को लंबवत बिसेक्ट करती हैं।
- ट्रेपेजियम
- केवल एक जोड़ी विपरीत भुजाएँ समानांतर हैं (AB || CD)।
- गैर-समानांतर भुजाएँ ट्रेपेजियम के पैर कहलाती हैं।
- आड़ा रेखाएँ समान अनुपात में एक-दूसरे को बिसेक्ट नहीं करती हैं।
- पतंग
- दो जोड़े सन्निकट भुजाएँ समान हैं (AB = AD, BC = CD)।
- आड़ा रेखाएँ 90 डिग्री पर एक-दूसरे को मिलती हैं।
- एक आड़ा रेखा दूसरी को बिसेक्ट करती है।
परिभाषा: एक चतुर्भुज जिसमें दो जोड़े विपरीत भुजाएँ समानांतर और समान लंबाई की होती हैं।
परिभाषा: एक पैरालेलोग्राम जिसमें प्रत्येक कोण 90 डिग्री होता है।
परिभाषा: एक पैरालेलोग्राम जिसमें सभी भुजाएँ समान और प्रत्येक कोण 90 डिग्री का होता है।
परिभाषा: एक पैरालेलोग्राम जिसमें सभी भुजाएँ समान होती हैं, और आड़ा रेखाएँ एक-दूसरे को 90 डिग्री पर बिसेक्ट करती हैं।
परिभाषा: एक चतुर्भुज जिसमें केवल एक जोड़ी विपरीत भुजाएँ समानांतर होती हैं।
परिभाषा: एक चतुर्भुज जिसमें दो जोड़े सन्निकट भुजाएँ समान लंबाई की होती हैं।
चतुर्भुज का सूत्र
चतुर्भुज सूत्र
पैरालेलोग्राम: 2 × (समीपवर्ती भुजाओं की लंबाई का योग)। 2 × (आधार भुजा) 2 × (समीपवर्ती भुजाओं की लंबाई का योग)। 2 × (आधार भुजा)- 2 × (समीपवर्ती भुजाओं की लंबाई का योग)। 2 × (आधार भुजा)
- 2 × (आधार भुजा)
- 2 × (L B) = 2 × (लंबाई × चौड़ाई)
- 2 × (a a) = 4a (भुजा की लंबाई का 4 गुना)
- 2 × (भुजा की लंबाई 1 × भुजा की लंबाई 2)
- 2 (x y) (जहां, x और y समीपवर्ती जोड़े को दर्शाते हैं)
चौकोर आकृति का क्षेत्रफल
एक चौकोर आकृति का क्षेत्रफल उस कुल स्थान का माप है जो यह占 करती है। विभिन्न आकृतियों के लिए क्षेत्रफल के सूत्र निम्नलिखित हैं:
- वर्ग: सभी भुजाएँ समान होती हैं। क्षेत्रफल = भुजा × भुजा
- समांतर चतुर्भुज: विपरीत भुजाएँ समानांतर होती हैं। क्षेत्रफल = आधार × ऊँचाई
- आयत: विपरीत भुजाएँ समान होती हैं और सभी कोण 90 डिग्री होते हैं। क्षेत्रफल = लंबाई × चौड़ाई
- रोमबस: सभी भुजाएँ समान होती हैं, विपरीत कोण समान होते हैं। क्षेत्रफल = (तिर्यक1 × तिर्यक2) / 2
- ट्रैपेजियम: एक जोड़ी समानांतर भुजाएँ होती हैं। क्षेत्रफल = 0.5 × (समानांतर भुजाओं का योग) × ऊँचाई
- पतंग: दो जोड़े समीपस्थ भुजाएँ समान होती हैं। क्षेत्रफल = 0.5 × (तिर्यक1 × तिर्यक2)
आकृति | क्षेत्रफल
- समांतर चतुर्भुज: b × h (आधार × ऊँचाई)
- आयत: लंबाई × चौड़ाई ( L × B)
- वर्ग: a² (भुजा की लम्बाई का वर्ग)
- रोमबस: 1/2 × d1 × d2 (जहाँ दो तिर्यक की लम्बाई d1 और d2 है)
- ट्रैपेजियम: 1/2 × (समानांतर भुजाओं की लम्बाई का योग) × h (जहाँ, 'h' ऊँचाई का प्रतिनिधित्व करता है)
- पतंग: 1/2 × तिर्यक1 × तिर्यक2
चौकोर आकृतियों के भुजाएँ और कोण
समांतर चतुर्भुज, आयत, वर्ग, रोमबस, और ट्रैपेजियम के भुजाएँ और कोणों पर महत्वपूर्ण तथ्य जानें।
- विपरीत भुजाएँ एक-दूसरे के समानांतर होती हैं और कोने से कोने तक की रेखाएँ उन्हें दो भागों में काटती हैं।
- कोणों के माप अलग-अलग होते हैं, लेकिन विपरीत कोण समान होते हैं।
आकृति | भुजाएँ | कोण
- समांतर चतुर्भुज: विपरीत भुजाएँ समानांतर होती हैं और कोने से कोने तक की रेखाएँ उन्हें दो भागों में काटती हैं। विपरीत कोण समान होते हैं।
- आयत: विपरीत भुजाएँ समान और समानांतर होती हैं। सभी कोण समान होते हैं।
- वर्ग: सभी भुजाएँ समान लम्बाई की होती हैं। विपरीत भुजाएँ समानांतर होती हैं।
- रोमबस: चारों भुजाएँ समान होती हैं। विपरीत भुजाएँ समानांतर होती हैं।
- ट्रैपेजियम: सभी भुजाएँ अलग-अलग लम्बाई की होती हैं, जिसमें एक जोड़ी भुजाएँ समानांतर होती हैं।
चौकोर आकृतियों के गुण
चौकोर आकृतियों के सामान्य गुण:
- चौकोर आकृतियों में चार भुजाएँ होती हैं।
- चौकोर आकृतियों में चार शीर्ष होते हैं।
- चौकोर आकृतियों में दो तिर्यक होते हैं।
- सभी आंतरिक कोणों का योग 360 डिग्री होता है।
 |
Download the notes
चतुर्भुज: अवलोकन और उदाहरण
|
Download as PDF |
Download as PDF
प्रत्येक प्रकार के चौकोर आकृति के गुण
आकृति | गुण
- वर्ग: वर्ग की सभी भुजाएँ समान होती हैं। सभी आंतरिक कोण 90 डिग्री होते हैं।
- आयत: विपरीत भुजाएँ समान और समानांतर होती हैं। सभी आंतरिक कोण 90 डिग्री होते हैं।
- रोमबस: चारों भुजाएँ समान होती हैं। विपरीत कोण समान होते हैं।
- समांतर चतुर्भुज: विपरीत भुजाएँ समान और समानांतर होती हैं।
- ट्रैपेजियम: केवल एक जोड़ी विपरीत भुजाएँ समानांतर होती हैं।
- पतंग: समीपस्थ भुजाएँ समान होती हैं।
 |
Take a Practice Test
Test yourself on topics from Bank Exams exam
|
Practice Now |
Practice Now
चौकोर आकृतियों पर हल किए गए उदाहरण
एक बहुकोण एक सपाट आकृति होती है जिसमें कई भुजाएँ होती हैं। उदाहरण के लिए, तीन भुजाओं वाली आकृति को 3-गोन कहा जाता है, और चार भुजाओं वाली आकृति को 4-गोन कहा जाता है। यह लेख चौकोर आकृतियों पर केंद्रित है, जो चार भुजाओं वाले बहुकोण होते हैं। चौकोर आकृति के सभी आंतरिक कोणों का योग 360 डिग्री होता है।
यहाँ कुछ हल किए गए उदाहरण दिए गए हैं:
- उदाहरण 1: चार भुजाओं वाली आकृति का परिधि ज्ञात करें जिसकी भुजाएँ 6 सेमी, 7 सेमी, 8 सेमी और 13 सेमी हैं।
समाधान: दी गई भुजाओं की माप: 6 सेमी, 7 सेमी, 8 सेमी, और 13 सेमी।
परिधि = 6 + 7 + 8 + 13 = 34 सेमी। - उदाहरण 2: यदि एक पतंग के दो तिर्यक 22 सेमी और 6 सेमी लंबाई के हैं, तो उसका क्षेत्रफल ज्ञात करें।
समाधान: पतंग का क्षेत्रफल = 1/2 × तिर्यक1 × तिर्यक2 = 1/2 × 22 × 6 = 66 वर्ग सेमी। - उदाहरण 3: उस समांतर चतुर्भुज का परिधि ज्ञात करें जिसकी विपरीत भुजाएँ 13 सेमी और 6 सेमी हैं।
समाधान: समांतर चतुर्भुज की भुजाओं की पहचान के अनुसार, परिधि = 13 + 6 + 13 + 6 = 38 सेमी। - उदाहरण 4: एक आयत का आधार ज्ञात करें जिसका क्षेत्रफल 72 वर्ग यूनिट है और ऊँचाई 8 यूनिट है।
समाधान: दी गई जानकारी: क्षेत्रफल = 72 वर्ग यूनिट, ऊँचाई = 8 यूनिट।
आयत का क्षेत्रफल = आधार × ऊँचाई = 72 = आधार × 8, आधार = 72/8 = 9 यूनिट।
The document चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams is a part of the Bank Exams Course Quantitative Aptitude/संख्यात्मक योग्यता.
All you need of Bank Exams at this link: Bank Exams
|
171 docs|185 tests
|
Related Exams
About this Document
Mar 29, 2025
Last updated
Document Description: चतुर्भुज: अवलोकन और उदाहरण for Bank Exams 2025 is part of Quantitative Aptitude/संख्यात्मक योग्यता preparation.
The notes and questions for चतुर्भुज: अवलोकन और उदाहरण have been prepared according to the Bank Exams exam syllabus. Information about चतुर्भुज: अवलोकन और उदाहरण covers topics
like चतुर्भुज के प्रकार, चतुर्भुज सूत्र, चौकोर आकृति का क्षेत्रफल, चौकोर आकृतियों के भुजाएँ और कोण, चौकोर आकृतियों के गुण, प्रत्येक प्रकार के चौकोर आकृति के गुण, चौकोर आकृतियों पर हल किए गए उदाहरण and चतुर्भुज: अवलोकन और उदाहरण Example, for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for चतुर्भुज: अवलोकन और उदाहरण.
Introduction of चतुर्भुज: अवलोकन और उदाहरण in English is available as part of our Quantitative Aptitude/संख्यात्मक योग्यता
for Bank Exams & चतुर्भुज: अवलोकन और उदाहरण in Hindi for Quantitative Aptitude/संख्यात्मक योग्यता course.
Download more important topics related with notes, lectures and mock test series for Bank Exams
Exam by signing up for free. Bank Exams: चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
Description
Full syllabus notes, lecture & questions for चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams - Bank Exams | Plus excerises question with solution to help you revise complete syllabus for Quantitative Aptitude/संख्यात्मक योग्यता | Best notes, free PDF download
Information about चतुर्भुज: अवलोकन और उदाहरण
In this doc you can find the meaning of चतुर्भुज: अवलोकन और उदाहरण defined & explained in the simplest way possible. Besides explaining types of
चतुर्भुज: अवलोकन और उदाहरण theory, EduRev gives you an ample number of questions to practice चतुर्भुज: अवलोकन और उदाहरण tests, examples and also practice Bank Exams
tests
Related Searches
Summary
,ppt
,Exam
,shortcuts and tricks
,MCQs
,mock tests for examination
,Semester Notes
,चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,past year papers
,Viva Questions
,practice quizzes
,चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,Previous Year Questions with Solutions
,Sample Paper
,study material
,Extra Questions
,चतुर्भुज: अवलोकन और उदाहरण | Quantitative Aptitude/संख्यात्मक योग्यता - Bank Exams
,Free
,video lectures
,Important questions
,Objective type Questions
;
Additional Information about चतुर्भुज: अवलोकन और उदाहरण for Bank Exams Preparation
चतुर्भुज: अवलोकन और उदाहरण Free PDF Download
The चतुर्भुज: अवलोकन और उदाहरण is an invaluable resource that delves deep into the core of the Bank Exams exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the चतुर्भुज: अवलोकन और उदाहरण now and kickstart your journey towards success in the Bank Exams exam.
Importance of चतुर्भुज: अवलोकन और उदाहरण
The importance of चतुर्भुज: अवलोकन और उदाहरण cannot be overstated, especially for Bank Exams aspirants.
This document holds the key to success in the Bank Exams exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
चतुर्भुज: अवलोकन और उदाहरण Notes
चतुर्भुज: अवलोकन और उदाहरण Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to चतुर्भुज: अवलोकन और उदाहरण.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, चतुर्भुज: अवलोकन और उदाहरण Notes on EduRev are your ultimate resource for success.
चतुर्भुज: अवलोकन और उदाहरण Bank Exams Questions
The "चतुर्भुज: अवलोकन और उदाहरण Bank Exams Questions" guide is a valuable resource for all aspiring students preparing for the
Bank Exams exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study चतुर्भुज: अवलोकन और उदाहरण on the App
Students of Bank Exams can study चतुर्भुज: अवलोकन और उदाहरण alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the चतुर्भुज: अवलोकन और उदाहरण,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of चतुर्भुज: अवलोकन और उदाहरण is prepared as per the latest Bank Exams syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily