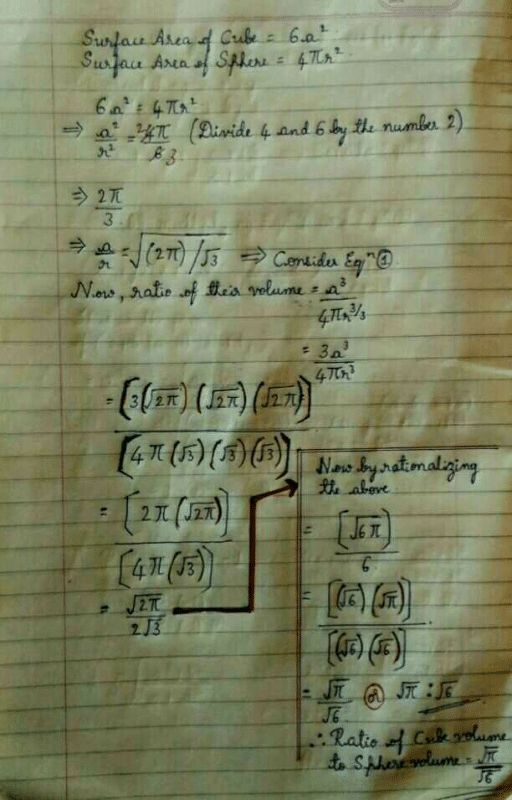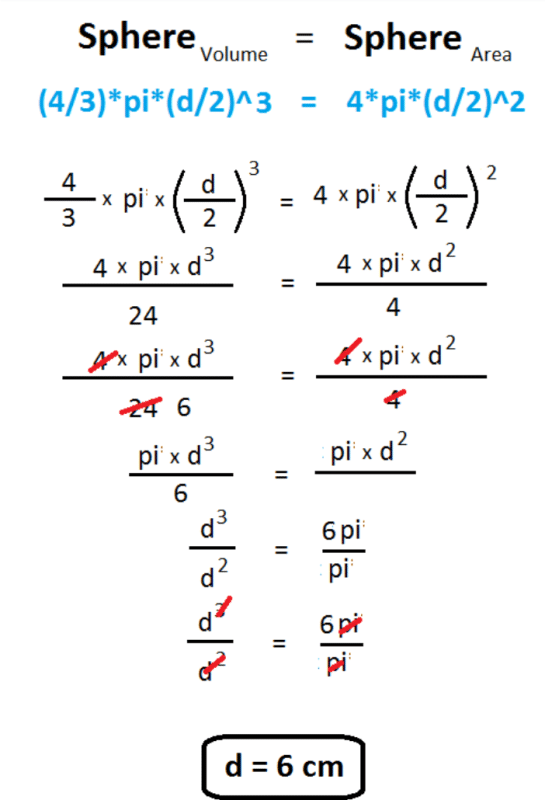All Exams >
Class 10 >
Weekly Tests for Class 10 Preparation >
All Questions
All questions of December Week 4 for Class 10 Exam
Conventional direction of electric current is from- a)Lower potential to higher potential
- b)Higher resistance to lower resistance
- c)Positive to negative terminal
- d)Negative to positive terminal
Correct answer is 'C'. Can you explain this answer?
Conventional direction of electric current is from
a)
Lower potential to higher potential
b)
Higher resistance to lower resistance
c)
Positive to negative terminal
d)
Negative to positive terminal
|
|
C K Academy answered |
The current in the wire is due to the drifting of electrons inside a wire in a direction opposite to the flow of electrons. During their drifting they collide with their atoms vibrating about their mean position and lose some of kinetic energy to the vibrating atoms.
The electrons are negatively charged particles and so, the electrons move towards the positively charged terminal from the negatively charged terminal.
Hence, the statement is true as the conventional direction of flow of current is from positive terminal to negative terminal of the cell.
The electrons are negatively charged particles and so, the electrons move towards the positively charged terminal from the negatively charged terminal.
Hence, the statement is true as the conventional direction of flow of current is from positive terminal to negative terminal of the cell.
Can you explain the answer of this question below:How much work is done, when 1 coulomb of charge moves against a potential difference of 1 volt?
- A:
1 joule
- B:
2 joule
- C:
0.5 joule
- D:
1.5 joule
The answer is a.
How much work is done, when 1 coulomb of charge moves against a potential difference of 1 volt?
1 joule
2 joule
0.5 joule
1.5 joule
|
|
Arun Yadav answered |
Charge moved, Q = 1 C
Potential difference, V = 1V
Therefore,
Work done, W = QV
= 1 C x 1 V
= 1 joule.
A bulb draws a current of 0.20 A for 15 minutes. What is the amount of electric charge that flows through it ?
- a)180 C
- b)182 C
- c)200 C
- d)300 C
Correct answer is option 'A'. Can you explain this answer?
A bulb draws a current of 0.20 A for 15 minutes. What is the amount of electric charge that flows through it ?
a)
180 C
b)
182 C
c)
200 C
d)
300 C
|
|
Rajiv Gupta answered |
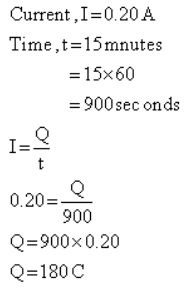
The amount of electric charge that flows through the bulb =180 C.
The opposing capacity of materials against the current flow is- a)Conductance
- b)Inductance
- c)Susceptance
- d)Resistance
Correct answer is option 'D'. Can you explain this answer?
The opposing capacity of materials against the current flow is
a)
Conductance
b)
Inductance
c)
Susceptance
d)
Resistance
|
|
Rahul Kapoor answered |
The electrical resistance of an electrical conductor is a measure of the difficulty to pass an electric current through that conductor.
Resistance in a conductor can be defined as the opposition offered to the flow of electrons. For a conductor of uniform cross-sectional area resistance is directly proportional to the length of the conductor and inversely proportional to the cross-sectional area of the conductor.
A container is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 24 cm and the total height of the container is 16 cm. Its capacity is- a)5390.60 cm3
- b)5100 cm3
- c)5400 cm3
- d)5425.92 cm3
Correct answer is option 'D'. Can you explain this answer?
A container is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter of the sphere is 24 cm and the total height of the container is 16 cm. Its capacity is
a)
5390.60 cm3
b)
5100 cm3
c)
5400 cm3
d)
5425.92 cm3
|
|
Meghana shah answered |
To find the capacity of the container, we need to calculate the volume of the hemispherical bowl and the volume of the cylinder separately, and then add them together.
Given:
Diameter of the sphere = 24 cm
Total height of the container = 16 cm
**Calculating the Volume of the Hemispherical Bowl:**
The radius of the sphere (r) can be calculated by dividing the diameter by 2.
r = 24 cm / 2 = 12 cm
The volume of a hemisphere is given by the formula:
V_hemisphere = (2/3) * π * r^3
Substituting the value of r, we get:
V_hemisphere = (2/3) * π * 12^3
Calculating this value, we find:
V_hemisphere ≈ 3617.92 cm^3
**Calculating the Volume of the Cylinder:**
The height of the cylinder can be calculated by subtracting the radius of the sphere from the total height of the container.
Height of the cylinder = Total height of the container - Radius of the sphere
Height of the cylinder = 16 cm - 12 cm = 4 cm
The radius of the cylinder is the same as the radius of the sphere, which is 12 cm.
The volume of a cylinder is given by the formula:
V_cylinder = π * r^2 * h
Substituting the values of r and h, we get:
V_cylinder = π * 12^2 * 4
Calculating this value, we find:
V_cylinder ≈ 1809.28 cm^3
**Calculating the Total Capacity:**
The total capacity of the container is the sum of the volume of the hemisphere and the volume of the cylinder.
Total capacity = V_hemisphere + V_cylinder
Total capacity ≈ 3617.92 cm^3 + 1809.28 cm^3
Calculating this value, we find:
Total capacity ≈ 5427.20 cm^3
Rounding off to two decimal places, we get:
Total capacity ≈ 5425.92 cm^3
Therefore, the correct answer is option D) 5425.92 cm^3.
Given:
Diameter of the sphere = 24 cm
Total height of the container = 16 cm
**Calculating the Volume of the Hemispherical Bowl:**
The radius of the sphere (r) can be calculated by dividing the diameter by 2.
r = 24 cm / 2 = 12 cm
The volume of a hemisphere is given by the formula:
V_hemisphere = (2/3) * π * r^3
Substituting the value of r, we get:
V_hemisphere = (2/3) * π * 12^3
Calculating this value, we find:
V_hemisphere ≈ 3617.92 cm^3
**Calculating the Volume of the Cylinder:**
The height of the cylinder can be calculated by subtracting the radius of the sphere from the total height of the container.
Height of the cylinder = Total height of the container - Radius of the sphere
Height of the cylinder = 16 cm - 12 cm = 4 cm
The radius of the cylinder is the same as the radius of the sphere, which is 12 cm.
The volume of a cylinder is given by the formula:
V_cylinder = π * r^2 * h
Substituting the values of r and h, we get:
V_cylinder = π * 12^2 * 4
Calculating this value, we find:
V_cylinder ≈ 1809.28 cm^3
**Calculating the Total Capacity:**
The total capacity of the container is the sum of the volume of the hemisphere and the volume of the cylinder.
Total capacity = V_hemisphere + V_cylinder
Total capacity ≈ 3617.92 cm^3 + 1809.28 cm^3
Calculating this value, we find:
Total capacity ≈ 5427.20 cm^3
Rounding off to two decimal places, we get:
Total capacity ≈ 5425.92 cm^3
Therefore, the correct answer is option D) 5425.92 cm^3.
A cone and a cylinder have their heights in the ratio 4: 5 and their diameters are in the ratio 3: 2. The ratio of their volumes will be- a)6: 7
- b)4: 3
- c)3: 5
- d)5: 3
Correct answer is option 'C'. Can you explain this answer?
A cone and a cylinder have their heights in the ratio 4: 5 and their diameters are in the ratio 3: 2. The ratio of their volumes will be
a)
6: 7
b)
4: 3
c)
3: 5
d)
5: 3
|
|
Ananya Das answered |
Height of cone =4x
Height of cylinder=5x
Diameter of cone=3y
Diameter of cylinder=2y
Volume of cone=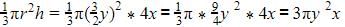 Volume of cylinder= πr2h=y2*5x
Volume of cylinder= πr2h=y2*5x
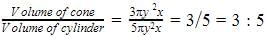
Height of cylinder=5x
Diameter of cone=3y
Diameter of cylinder=2y
Volume of cone=
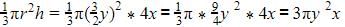 Volume of cylinder= πr2h=y2*5x
Volume of cylinder= πr2h=y2*5x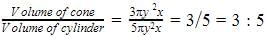
The symbol used for representing Independent sources- a)Diamond
- b)Square
- c)Circle
- d)Triangle
Correct answer is option 'C'. Can you explain this answer?
The symbol used for representing Independent sources
a)
Diamond
b)
Square
c)
Circle
d)
Triangle
|
|
Amit Sharma answered |
Independent sources are represented by circle
Dependent sources are represented by Diamond.
Dependent sources are represented by Diamond.
A cylinder, a cone and a hemisphere are of equal base and have the same height. The ratio of their volumes is
- a)4: 5: 7
- b)3: 2: 1
- c)1: 2:3
- d)3: 1: 2
Correct answer is option 'D'. Can you explain this answer?
A cylinder, a cone and a hemisphere are of equal base and have the same height. The ratio of their volumes is
a)
4: 5: 7
b)
3: 2: 1
c)
1: 2:3
d)
3: 1: 2

|
Abhishek Kumar Pandey answered |
According to me, Option D is not the right answer.....
option B is the right answer.
I am sorry because I couldn't able to attach the solution...
solution:
let r be the radius and h be the height.
so, ratio of volume of cylinder,cone& hemisphere=
πr²h: 1/3πr²h:2/3πr³
(since h=r)
=> πr³:1/3πr³:2/3πr³
=>1:1/3:2/3
=>3:1:2
your explanation.
A cylinder, a cone and a hemisphere have equal base and height. Find the ratio of their volumes- a)1:1:1
- b)2:3:1
- c)3 :1 :2
- d)1:2:3
Correct answer is option 'C'. Can you explain this answer?
A cylinder, a cone and a hemisphere have equal base and height. Find the ratio of their volumes
a)
1:1:1
b)
2:3:1
c)
3 :1 :2
d)
1:2:3
|
|
Nandini jain answered |
**Given**
- A cylinder, a cone, and a hemisphere have equal base and height.
**To Find**
- The ratio of their volumes.
**Solution**
Let's assume the height and base radius of each shape to be 'h' and 'r', respectively.
**Volume of a Cylinder**
The volume of a cylinder is given by the formula:
Vcylinder = πr^2h
**Volume of a Cone**
The volume of a cone is given by the formula:
Vcone = (1/3)πr^2h
**Volume of a Hemisphere**
The volume of a hemisphere is given by the formula:
Vhemisphere = (2/3)πr^3
**Given Conditions**
- The base radius and height of the cylinder, cone, and hemisphere are equal.
- So, r = h for all three shapes.
**Substituting Values**
Substituting r = h in the volume formulas for each shape, we get:
Vcylinder = πr^2h = πh^2h = πh^3
Vcone = (1/3)πr^2h = (1/3)πh^2h = (1/3)πh^3
Vhemisphere = (2/3)πr^3 = (2/3)πh^3
**Comparing Volumes**
The ratio of the volumes of the cylinder, cone, and hemisphere can be found by dividing each volume by the volume of the cylinder (since the cylinder has the largest volume):
Ratio = (Vcylinder : Vcone : Vhemisphere) / Vcylinder
= (πh^3 : (1/3)πh^3 : (2/3)πh^3) / πh^3
= 1 : (1/3) : (2/3)
= 3 : 1 : 2
Therefore, the ratio of their volumes is 3 : 1 : 2. The correct answer is option 'C'.
- A cylinder, a cone, and a hemisphere have equal base and height.
**To Find**
- The ratio of their volumes.
**Solution**
Let's assume the height and base radius of each shape to be 'h' and 'r', respectively.
**Volume of a Cylinder**
The volume of a cylinder is given by the formula:
Vcylinder = πr^2h
**Volume of a Cone**
The volume of a cone is given by the formula:
Vcone = (1/3)πr^2h
**Volume of a Hemisphere**
The volume of a hemisphere is given by the formula:
Vhemisphere = (2/3)πr^3
**Given Conditions**
- The base radius and height of the cylinder, cone, and hemisphere are equal.
- So, r = h for all three shapes.
**Substituting Values**
Substituting r = h in the volume formulas for each shape, we get:
Vcylinder = πr^2h = πh^2h = πh^3
Vcone = (1/3)πr^2h = (1/3)πh^2h = (1/3)πh^3
Vhemisphere = (2/3)πr^3 = (2/3)πh^3
**Comparing Volumes**
The ratio of the volumes of the cylinder, cone, and hemisphere can be found by dividing each volume by the volume of the cylinder (since the cylinder has the largest volume):
Ratio = (Vcylinder : Vcone : Vhemisphere) / Vcylinder
= (πh^3 : (1/3)πh^3 : (2/3)πh^3) / πh^3
= 1 : (1/3) : (2/3)
= 3 : 1 : 2
Therefore, the ratio of their volumes is 3 : 1 : 2. The correct answer is option 'C'.
What is one reason why the World Bank’s per capita income criterion for classifying countries has limitations?- a)It includes only economic factors.
- b)It does not account for income distribution.
- c)It considers environmental factors.
- d)It measures non-monetary aspects.
Correct answer is option 'B'. Can you explain this answer?
a)
It includes only economic factors.
b)
It does not account for income distribution.
c)
It considers environmental factors.
d)
It measures non-monetary aspects.

|
Kamna Science Academy answered |
The World Bank’s per capita income criterion has limitations because it does not account for income distribution. This means it may overlook significant disparities in income within a country, which can affect the overall well-being of its population despite a high average income.
Difficult Level
Difficult Level
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the a hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of the water left in the tub.- a)200 cm3
- b)600 cm3
- c)550 cm3
- d)616 cm3
Correct answer is option 'D'. Can you explain this answer?
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the a hemisphere is 3.5 cm and height of cone outside the hemisphere is 5 cm, find the volume of the water left in the tub.
a)
200 cm3
b)
600 cm3
c)
550 cm3
d)
616 cm3
|
|
Rajeev Chavan answered |
Given:
Radius of cylindrical tub, r = 5 cm
Length of cylindrical tub, l = 9.8 cm
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
To find: Volume of the water left in the tub
Approach:
First, we find the total volume of the cylindrical tub.
Then, we find the volume of the solid (cone mounted on a hemisphere) that is immersed in the tub.
Finally, we subtract the volume of the solid from the total volume of the tub to get the volume of the water left in the tub.
Calculation:
1. Volume of the cylindrical tub
Given,
Radius of the cylindrical tub, r = 5 cm
Length of the cylindrical tub, l = 9.8 cm
The formula for the volume of a cylinder is:
V_cylinder = πr^2l
Substituting the given values, we get:
V_cylinder = π(5)^2(9.8) = 245π cm^3
2. Volume of the solid (cone mounted on a hemisphere)
Given,
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
The solid consists of a cone mounted on a hemisphere. We can find the volume of the solid by adding the volumes of the cone and the hemisphere.
The formula for the volume of a cone is:
V_cone = 1/3πr^2h
Substituting the given values, we get:
V_cone = 1/3π(3.5)^2(5) = 61.25π/3 cm^3
The formula for the volume of a hemisphere is:
V_hemisphere = 2/3πR^3
Substituting the given values, we get:
V_hemisphere = 2/3π(3.5)^3 = 42.875π/3 cm^3
Therefore, the volume of the solid is:
V_solid = V_cone + V_hemisphere = 61.25π/3 + 42.875π/3 = 104.125π/3 cm^3
3. Volume of the water left in the tub
The volume of the water left in the tub is the total volume of the cylindrical tub minus the volume of the solid that is immersed in the tub.
V_water = V_cylinder - V_solid
V_water = 245π - 104.125π/3
V_water = 735/3π - 104.125/3π
V_water = (735 - 104.125)/3π
V_water = 216.875/3π cm^3
V_water = 216.875/3 × 3.14
V_water = 616.06 cm^3
Therefore, the volume of the water left in the tub is 616.06 cm^3 (approximately).
Hence, the correct option is (d) 616 cm^3.
Radius of cylindrical tub, r = 5 cm
Length of cylindrical tub, l = 9.8 cm
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
To find: Volume of the water left in the tub
Approach:
First, we find the total volume of the cylindrical tub.
Then, we find the volume of the solid (cone mounted on a hemisphere) that is immersed in the tub.
Finally, we subtract the volume of the solid from the total volume of the tub to get the volume of the water left in the tub.
Calculation:
1. Volume of the cylindrical tub
Given,
Radius of the cylindrical tub, r = 5 cm
Length of the cylindrical tub, l = 9.8 cm
The formula for the volume of a cylinder is:
V_cylinder = πr^2l
Substituting the given values, we get:
V_cylinder = π(5)^2(9.8) = 245π cm^3
2. Volume of the solid (cone mounted on a hemisphere)
Given,
Radius of hemisphere, R = 3.5 cm
Height of cone outside the hemisphere, h = 5 cm
The solid consists of a cone mounted on a hemisphere. We can find the volume of the solid by adding the volumes of the cone and the hemisphere.
The formula for the volume of a cone is:
V_cone = 1/3πr^2h
Substituting the given values, we get:
V_cone = 1/3π(3.5)^2(5) = 61.25π/3 cm^3
The formula for the volume of a hemisphere is:
V_hemisphere = 2/3πR^3
Substituting the given values, we get:
V_hemisphere = 2/3π(3.5)^3 = 42.875π/3 cm^3
Therefore, the volume of the solid is:
V_solid = V_cone + V_hemisphere = 61.25π/3 + 42.875π/3 = 104.125π/3 cm^3
3. Volume of the water left in the tub
The volume of the water left in the tub is the total volume of the cylindrical tub minus the volume of the solid that is immersed in the tub.
V_water = V_cylinder - V_solid
V_water = 245π - 104.125π/3
V_water = 735/3π - 104.125/3π
V_water = (735 - 104.125)/3π
V_water = 216.875/3π cm^3
V_water = 216.875/3 × 3.14
V_water = 616.06 cm^3
Therefore, the volume of the water left in the tub is 616.06 cm^3 (approximately).
Hence, the correct option is (d) 616 cm^3.
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm and the heights of the cylindrical and conical portions are 12 cm and 7 cm respectively. The approximate volume of the toy will be- a)250 cm3
- b)200 cm3
- c)300 cm3
- d)218 cm3
Correct answer is option 'D'. Can you explain this answer?
A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm and the heights of the cylindrical and conical portions are 12 cm and 7 cm respectively. The approximate volume of the toy will be
a)
250 cm3
b)
200 cm3
c)
300 cm3
d)
218 cm3
|
|
Cat Warior answered |
D
A cylindrical vessel of diameter 42 cm and height 40 cm contains water up to a depth of 16 cm. Now a solid iron cylinder, with diameter 14 cm and height 32 cm is placed upright in the cylindrical vessel. The volume of the water required to just submerge the solid cylinder will be- a)17, 248 cm3
- b)14, 000 cm3
- c)15, 600 cm3
- d)16, 045 cm3
Correct answer is option 'A'. Can you explain this answer?
A cylindrical vessel of diameter 42 cm and height 40 cm contains water up to a depth of 16 cm. Now a solid iron cylinder, with diameter 14 cm and height 32 cm is placed upright in the cylindrical vessel. The volume of the water required to just submerge the solid cylinder will be
a)
17, 248 cm3
b)
14, 000 cm3
c)
15, 600 cm3
d)
16, 045 cm3

|
Tanishka Gupta answered |

How does the use of averages sometimes mask disparities within a population?- a)By averaging out individual variations and not reflecting income distribution.
- b)By including only economic data without considering social aspects.
- c)By focusing solely on historical data.
- d)By comparing multiple countries without normalization.
Correct answer is option 'A'. Can you explain this answer?
a)
By averaging out individual variations and not reflecting income distribution.
b)
By including only economic data without considering social aspects.
c)
By focusing solely on historical data.
d)
By comparing multiple countries without normalization.
|
|
Rahul agarwal answered |
Understanding Averages in Populations
The use of averages can often obscure the reality of disparities within a population. Here's a deeper look at how this occurs:
Averaging Out Individual Variations
- Averages provide a single value that represents a group, making it easy to understand overall trends.
- However, this single figure can mask significant variations among individuals. For example, in income distribution:
- If a small number of individuals earn extremely high incomes, they can elevate the average income significantly.
- Meanwhile, a larger group may earn much lower incomes, but their struggles are hidden when looking solely at the average.
Not Reflecting Income Distribution
- Averages do not indicate how income is distributed across a population.
- When wealth is concentrated in the hands of a few, the average income can give a false impression of financial health for the entire population.
Example of Disparities
- Consider a situation where:
- Five people earn $30,000, and one person earns $1,000,000.
- The average income is $170,000, which suggests a wealthy population, but in reality, the majority are struggling.
Conclusion
- Relying on averages can lead to misleading conclusions about the well-being of a population.
- Understanding the distribution of data and considering individual variations is crucial for a more accurate representation of societal conditions.
By focusing on averages alone, we risk overlooking the true experiences and challenges faced by many individuals within a group.
The use of averages can often obscure the reality of disparities within a population. Here's a deeper look at how this occurs:
Averaging Out Individual Variations
- Averages provide a single value that represents a group, making it easy to understand overall trends.
- However, this single figure can mask significant variations among individuals. For example, in income distribution:
- If a small number of individuals earn extremely high incomes, they can elevate the average income significantly.
- Meanwhile, a larger group may earn much lower incomes, but their struggles are hidden when looking solely at the average.
Not Reflecting Income Distribution
- Averages do not indicate how income is distributed across a population.
- When wealth is concentrated in the hands of a few, the average income can give a false impression of financial health for the entire population.
Example of Disparities
- Consider a situation where:
- Five people earn $30,000, and one person earns $1,000,000.
- The average income is $170,000, which suggests a wealthy population, but in reality, the majority are struggling.
Conclusion
- Relying on averages can lead to misleading conclusions about the well-being of a population.
- Understanding the distribution of data and considering individual variations is crucial for a more accurate representation of societal conditions.
By focusing on averages alone, we risk overlooking the true experiences and challenges faced by many individuals within a group.
In the context of human development, why might a country with a lower per capita income rank higher in terms of human development index (HDI)?- a)Due to high income inequality.
- b)Due to better healthcare and education.
- c)Due to lower average wages.
- d)Due to higher inflation rates.
Correct answer is option 'B'. Can you explain this answer?
a)
Due to high income inequality.
b)
Due to better healthcare and education.
c)
Due to lower average wages.
d)
Due to higher inflation rates.

|
Nk Classes answered |
A country with a lower per capita income might rank higher in terms of the human development index (HDI) due to better healthcare and education. HDI considers various factors such as life expectancy, education level, and health, which might be better in countries with lower per capita income but effective social policies.
Which of the following is a limitation of using per capita income as the sole measure of development?- a)It does not measure GDP growth.
- b)It ignores differences in cost of living and income inequality.
- c)It includes non-economic factors.
- d)It only considers employment rates.
Correct answer is option 'B'. Can you explain this answer?
a)
It does not measure GDP growth.
b)
It ignores differences in cost of living and income inequality.
c)
It includes non-economic factors.
d)
It only considers employment rates.

|
Gowri Mehta answered |
Limitation of Per Capita Income as a Measure of Development
Per capita income is often used as an indicator of a country's economic performance and overall development. However, relying solely on this measure has significant limitations, particularly regarding its ability to provide a comprehensive view of development.
Ignoring Cost of Living
- Per capita income does not account for variations in the cost of living across different regions.
- A higher income in one region may not translate to better living standards if the cost of goods and services is also high.
Overlooking Income Inequality
- This measure averages income across a population, which can mask disparities.
- A small percentage of the population may earn exceptionally high incomes, skewing the average and making it seem like the economy is doing well, even if the majority are living in poverty.
Exclusion of Non-Economic Factors
- Per capita income fails to consider qualitative aspects of development, such as education, healthcare, and environmental sustainability.
- These factors are crucial for a more holistic understanding of an individual's quality of life.
Employment Rates and Economic Structure
- While employment rates are important, per capita income does not specifically measure this aspect, which can be critical in assessing economic health and job opportunities.
In summary, while per capita income provides useful insights into economic performance, it is essential to consider other indicators to gain a complete picture of development, including cost of living, income distribution, and social well-being.
Per capita income is often used as an indicator of a country's economic performance and overall development. However, relying solely on this measure has significant limitations, particularly regarding its ability to provide a comprehensive view of development.
Ignoring Cost of Living
- Per capita income does not account for variations in the cost of living across different regions.
- A higher income in one region may not translate to better living standards if the cost of goods and services is also high.
Overlooking Income Inequality
- This measure averages income across a population, which can mask disparities.
- A small percentage of the population may earn exceptionally high incomes, skewing the average and making it seem like the economy is doing well, even if the majority are living in poverty.
Exclusion of Non-Economic Factors
- Per capita income fails to consider qualitative aspects of development, such as education, healthcare, and environmental sustainability.
- These factors are crucial for a more holistic understanding of an individual's quality of life.
Employment Rates and Economic Structure
- While employment rates are important, per capita income does not specifically measure this aspect, which can be critical in assessing economic health and job opportunities.
In summary, while per capita income provides useful insights into economic performance, it is essential to consider other indicators to gain a complete picture of development, including cost of living, income distribution, and social well-being.
Which aspect of human development is not directly reflected by per capita income?- a)Literacy rate
- b)Health status
- c)Environmental sustainability
- d)Economic output
Correct answer is option 'C'. Can you explain this answer?
a)
Literacy rate
b)
Health status
c)
Environmental sustainability
d)
Economic output
|
|
Nitish menon answered |
Understanding Per Capita Income
Per capita income is a widely used economic indicator that reflects the average income earned per person in a given area, typically a country. While it provides insight into the economic conditions of a population, it does not encompass all aspects of human development.
Aspects Not Reflected by Per Capita Income
- Literacy Rate: This measures the percentage of people who can read and write. High literacy rates contribute to a more informed and skilled workforce, essential for sustainable economic growth.
- Health Status: This includes life expectancy, access to healthcare, and overall well-being. A higher per capita income does not guarantee good health outcomes, as it does not account for the distribution of wealth or the quality of healthcare services.
- Environmental Sustainability: This is the focus of our explanation. Environmental sustainability refers to practices that do not deplete natural resources and ensure ecological balance. High per capita income can sometimes lead to increased consumption and waste, harming the environment. For instance, industrial growth may boost income but also lead to pollution and resource depletion, reflecting a lack of sustainable practices.
- Economic Output: This pertains to the total production of goods and services in an economy. It is related to per capita income but does not provide a complete picture of individual well-being or social equity.
Conclusion
In summary, while per capita income is a useful measure of economic prosperity, it fails to capture critical elements of human development, particularly environmental sustainability. Sustainable development requires a balance between economic growth and the preservation of ecological resources.
Per capita income is a widely used economic indicator that reflects the average income earned per person in a given area, typically a country. While it provides insight into the economic conditions of a population, it does not encompass all aspects of human development.
Aspects Not Reflected by Per Capita Income
- Literacy Rate: This measures the percentage of people who can read and write. High literacy rates contribute to a more informed and skilled workforce, essential for sustainable economic growth.
- Health Status: This includes life expectancy, access to healthcare, and overall well-being. A higher per capita income does not guarantee good health outcomes, as it does not account for the distribution of wealth or the quality of healthcare services.
- Environmental Sustainability: This is the focus of our explanation. Environmental sustainability refers to practices that do not deplete natural resources and ensure ecological balance. High per capita income can sometimes lead to increased consumption and waste, harming the environment. For instance, industrial growth may boost income but also lead to pollution and resource depletion, reflecting a lack of sustainable practices.
- Economic Output: This pertains to the total production of goods and services in an economy. It is related to per capita income but does not provide a complete picture of individual well-being or social equity.
Conclusion
In summary, while per capita income is a useful measure of economic prosperity, it fails to capture critical elements of human development, particularly environmental sustainability. Sustainable development requires a balance between economic growth and the preservation of ecological resources.
Conventional direction of electric current is from- a)Lower potential to higher potential
- b)Higher resistance to lower resistance
- c)Positive to negative terminal
- d)Negative to positive terminal
Correct answer is option 'C'. Can you explain this answer?
Conventional direction of electric current is from
a)
Lower potential to higher potential
b)
Higher resistance to lower resistance
c)
Positive to negative terminal
d)
Negative to positive terminal
|
|
Rahul Kapoor answered |
Conventional current flows out of the positive terminal of the voltage source, flows though the load or circuit elements and returns to negative terminal of the voltage source. Inside the voltage source, it flows from negative to positive terminal, and again flows our of the positive terminal.
In voltage sources, current always flow out of the positive terminal and enters into negative terminal after travelling through load / circuit elements. In load and circuit elements (other than voltage / current sources), voltage drop has positive polarity where the current enters and negative, where the current flows out.
A cylinder whose height is two thirds of its diameter has the same volume as a sphere of radius 4 cm. The radius of the base of the cylinder will be- a)4 cm
- b)2 cm
- c)5 cm
- d)8 cm
Correct answer is option 'A'. Can you explain this answer?
A cylinder whose height is two thirds of its diameter has the same volume as a sphere of radius 4 cm. The radius of the base of the cylinder will be
a)
4 cm
b)
2 cm
c)
5 cm
d)
8 cm
|
|
Animesh shah answered |
To solve this problem, we can use the formulas for the volume of a cylinder and the volume of a sphere. Let's break down the solution into steps:
Given information:
- The height of the cylinder is two-thirds of its diameter
- The volume of the cylinder is equal to the volume of a sphere with a radius of 4 cm
Step 1: Calculate the volume of the sphere
The formula for the volume of a sphere is V = (4/3)πr^3, where r is the radius. Since the radius of the sphere is given as 4 cm, we can substitute this value into the formula:
V_sphere = (4/3)π(4^3)
V_sphere = (4/3)π(64)
V_sphere = (4/3)(3.14)(64)
V_sphere ≈ 268.08 cm^3
Step 2: Set up the equation for the volume of the cylinder
The formula for the volume of a cylinder is V = πr^2h, where r is the radius and h is the height. We are given that the height of the cylinder is two-thirds of its diameter. Since the diameter is twice the radius, we can write the height as h = (2/3)(2r) = (4/3)r. Substituting these values into the formula, we get:
V_cylinder = πr^2(4/3)r
V_cylinder = (4/3)πr^3
Step 3: Equate the volumes of the cylinder and the sphere
Since the volume of the cylinder is equal to the volume of the sphere, we can set up the equation:
(4/3)πr^3 = 268.08
Dividing both sides by (4/3)π, we get:
r^3 = 268.08 / (4/3)π
r^3 = 201.06 / π
Taking the cube root of both sides, we find:
r = (201.06/π)^(1/3)
r ≈ 4 cm
Therefore, the radius of the base of the cylinder is approximately 4 cm, which corresponds to option A.
Given information:
- The height of the cylinder is two-thirds of its diameter
- The volume of the cylinder is equal to the volume of a sphere with a radius of 4 cm
Step 1: Calculate the volume of the sphere
The formula for the volume of a sphere is V = (4/3)πr^3, where r is the radius. Since the radius of the sphere is given as 4 cm, we can substitute this value into the formula:
V_sphere = (4/3)π(4^3)
V_sphere = (4/3)π(64)
V_sphere = (4/3)(3.14)(64)
V_sphere ≈ 268.08 cm^3
Step 2: Set up the equation for the volume of the cylinder
The formula for the volume of a cylinder is V = πr^2h, where r is the radius and h is the height. We are given that the height of the cylinder is two-thirds of its diameter. Since the diameter is twice the radius, we can write the height as h = (2/3)(2r) = (4/3)r. Substituting these values into the formula, we get:
V_cylinder = πr^2(4/3)r
V_cylinder = (4/3)πr^3
Step 3: Equate the volumes of the cylinder and the sphere
Since the volume of the cylinder is equal to the volume of the sphere, we can set up the equation:
(4/3)πr^3 = 268.08
Dividing both sides by (4/3)π, we get:
r^3 = 268.08 / (4/3)π
r^3 = 201.06 / π
Taking the cube root of both sides, we find:
r = (201.06/π)^(1/3)
r ≈ 4 cm
Therefore, the radius of the base of the cylinder is approximately 4 cm, which corresponds to option A.
Volume of a hollow right circular cylinder is- a)πr2h (R2 + r2)
- b)πr2h (R2 – r2)
- c)πrh (R2 – r2)
- d)πh (R2 – r2)
Correct answer is option 'D'. Can you explain this answer?
Volume of a hollow right circular cylinder is
a)
πr2h (R2 + r2)
b)
πr2h (R2 – r2)
c)
πrh (R2 – r2)
d)
πh (R2 – r2)
|
|
Ritu gupta answered |
Πr²h - πr₁²h
where r is the outer radius, r₁ is the inner radius, and h is the height of the cylinder.
where r is the outer radius, r₁ is the inner radius, and h is the height of the cylinder.
The radii of two right circular cylinders are in the ratio 2: 3 and their heights are in the ratio 5: 4. The ratio of their volumes will be- a)4: 3
- b)6: 7
- c)5: 9
- d)2: 3
Correct answer is option 'C'. Can you explain this answer?
The radii of two right circular cylinders are in the ratio 2: 3 and their heights are in the ratio 5: 4. The ratio of their volumes will be
a)
4: 3
b)
6: 7
c)
5: 9
d)
2: 3
|
|
Naveen Gupta answered |
Ratio of Radii:
Let the radii of the two cylinders be 2x and 3x.
Ratio of Heights:
Let the heights of the two cylinders be 5y and 4y.
Volume of a Cylinder:
The volume of a cylinder is given by the formula V = πr²h, where r is the radius and h is the height.
Finding the Volumes:
The volume of the first cylinder with radius 2x and height 5y is V₁ = π(2x)²(5y) = 20πx²y.
The volume of the second cylinder with radius 3x and height 4y is V₂ = π(3x)²(4y) = 36πx²y.
Ratio of Volumes:
The ratio of the volumes of the two cylinders is given by V₁ : V₂.
Substituting the values, we get V₁ : V₂ = 20πx²y : 36πx²y.
Simplifying, we get V₁ : V₂ = 5x²y : 9x²y.
Dividing both sides by x²y, we get V₁ : V₂ = 5 : 9.
Therefore, the ratio of the volumes of the two cylinders is 5 : 9, which corresponds to option C.
Let the radii of the two cylinders be 2x and 3x.
Ratio of Heights:
Let the heights of the two cylinders be 5y and 4y.
Volume of a Cylinder:
The volume of a cylinder is given by the formula V = πr²h, where r is the radius and h is the height.
Finding the Volumes:
The volume of the first cylinder with radius 2x and height 5y is V₁ = π(2x)²(5y) = 20πx²y.
The volume of the second cylinder with radius 3x and height 4y is V₂ = π(3x)²(4y) = 36πx²y.
Ratio of Volumes:
The ratio of the volumes of the two cylinders is given by V₁ : V₂.
Substituting the values, we get V₁ : V₂ = 20πx²y : 36πx²y.
Simplifying, we get V₁ : V₂ = 5x²y : 9x²y.
Dividing both sides by x²y, we get V₁ : V₂ = 5 : 9.
Therefore, the ratio of the volumes of the two cylinders is 5 : 9, which corresponds to option C.
Chapter doubts & questions for December Week 4 - Weekly Tests for Class 10 Preparation 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of December Week 4 - Weekly Tests for Class 10 Preparation in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup