All Exams >
JEE >
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 >
All Questions
All questions of Mathematics for JEE Exam
A line passing through point A(-5,-4) meet other three lines x + 3y + 2 = 0, 2x + y + 4 = 0 and x - y - 5 = 0 at B, C and D respectively. If ( 15 AB )2 + ( 10 AC )2 = ( 6 AD )2, then the equation of line is- a)2x+3y+22=0
- b)5x-4y+7=0
- c)3x-2y+3=0
- d)3x+2y+3=0
Correct answer is option 'A'. Can you explain this answer?
A line passing through point A(-5,-4) meet other three lines x + 3y + 2 = 0, 2x + y + 4 = 0 and x - y - 5 = 0 at B, C and D respectively. If ( 15 AB )2 + ( 10 AC )2 = ( 6 AD )2, then the equation of line is
a)
2x+3y+22=0
b)
5x-4y+7=0
c)
3x-2y+3=0
d)
3x+2y+3=0
|
Amar Mehta answered |
Given Information:
Point A(-5,-4)
Equations of lines: x + 3y + 2 = 0, 2x + y + 4 = 0, and x - y - 5 = 0
(15AB)^2 + (10AC)^2 = (6AD)^2
Solution:
To find the equation of the line passing through point A and meeting lines x + 3y + 2 = 0, 2x + y + 4 = 0, and x - y - 5 = 0 at points B, C, and D respectively, we will follow these steps:
1. Find the coordinates of points B, C, and D by solving the equations of the given lines simultaneously with the line passing through point A.
2. Use the distance formula to calculate the lengths AB, AC, and AD.
3. Substitute the lengths in the given equation (15AB)^2 + (10AC)^2 = (6AD)^2.
4. Solve for the coefficients of the line passing through point A.
Calculations:
1. By solving the equations of the given lines with the line passing through A(-5,-4), we get:
B(-8,1), C(-7,1), D(-3,-2)
2. Calculate the lengths AB, AC, and AD:
AB = √((-8 - (-5))^2 + (1 - (-4))^2) = √(3^2 + 5^2) = √(9 + 25) = √34
AC = √((-7 - (-5))^2 + (1 - (-4))^2) = √(2^2 + 5^2) = √(4 + 25) = √29
AD = √((-3 - (-5))^2 + (-2 - (-4))^2) = √(2^2 + 2^2) = √(4 + 4) = √8
3. Substitute the lengths in the given equation:
(15√34)^2 + (10√29)^2 = (6√8)^2
(15^2)(34) + (10^2)(29) = (6^2)(8)
5100 + 2900 = 288
8000 = 8000
4. The coefficients of the line passing through A are 2x + 3y + 22 = 0.
Therefore, the correct answer is option A (2x + 3y + 22 = 0).
Point A(-5,-4)
Equations of lines: x + 3y + 2 = 0, 2x + y + 4 = 0, and x - y - 5 = 0
(15AB)^2 + (10AC)^2 = (6AD)^2
Solution:
To find the equation of the line passing through point A and meeting lines x + 3y + 2 = 0, 2x + y + 4 = 0, and x - y - 5 = 0 at points B, C, and D respectively, we will follow these steps:
1. Find the coordinates of points B, C, and D by solving the equations of the given lines simultaneously with the line passing through point A.
2. Use the distance formula to calculate the lengths AB, AC, and AD.
3. Substitute the lengths in the given equation (15AB)^2 + (10AC)^2 = (6AD)^2.
4. Solve for the coefficients of the line passing through point A.
Calculations:
1. By solving the equations of the given lines with the line passing through A(-5,-4), we get:
B(-8,1), C(-7,1), D(-3,-2)
2. Calculate the lengths AB, AC, and AD:
AB = √((-8 - (-5))^2 + (1 - (-4))^2) = √(3^2 + 5^2) = √(9 + 25) = √34
AC = √((-7 - (-5))^2 + (1 - (-4))^2) = √(2^2 + 5^2) = √(4 + 25) = √29
AD = √((-3 - (-5))^2 + (-2 - (-4))^2) = √(2^2 + 2^2) = √(4 + 4) = √8
3. Substitute the lengths in the given equation:
(15√34)^2 + (10√29)^2 = (6√8)^2
(15^2)(34) + (10^2)(29) = (6^2)(8)
5100 + 2900 = 288
8000 = 8000
4. The coefficients of the line passing through A are 2x + 3y + 22 = 0.
Therefore, the correct answer is option A (2x + 3y + 22 = 0).
the number of terms free from radicals is
The number of 4-digit even numbers that can be formed using 0, 1, 2, 3, 4, 5, 6 without repetition is- a)120
- b)300
- c)420
- d)20
Correct answer is option 'C'. Can you explain this answer?
The number of 4-digit even numbers that can be formed using 0, 1, 2, 3, 4, 5, 6 without repetition is
a)
120
b)
300
c)
420
d)
20
|
Veda Institute answered |
Each even number must have 0, 2, 4 or 6 in is units place
Here total number of digits = 7
When 0 occurs at units place there is no restriction on other places and when 2 or 4 occurs at units place there is restriction on thousands' place as 0 can not be put at thousands' place
Case I When 0 occurs at units place:
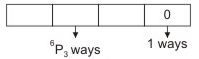
∴ The number of numbers formed in this case
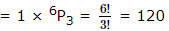
Case II. When 0 does not occur at units place:
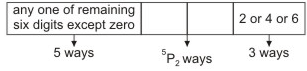
The units' place can be filled up by any one of the three digits 2, 4 and 6 in 3 ways
∴ The number of numbers formed in this case
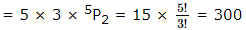
∴ The required number = 120 + 300 = 420
Here total number of digits = 7
When 0 occurs at units place there is no restriction on other places and when 2 or 4 occurs at units place there is restriction on thousands' place as 0 can not be put at thousands' place
Case I When 0 occurs at units place:
∴ The number of numbers formed in this case
Case II. When 0 does not occur at units place:
The units' place can be filled up by any one of the three digits 2, 4 and 6 in 3 ways
∴ The number of numbers formed in this case
∴ The required number = 120 + 300 = 420
From a group of 6 men and 4 women a committee of 4 persons is to be formed. In how many different ways can it be done so that the committee has at least 2 men?- a)210
- b)225
- c)195
- d)185
Correct answer is option 'D'. Can you explain this answer?
From a group of 6 men and 4 women a committee of 4 persons is to be formed. In how many different ways can it be done so that the committee has at least 2 men?
a)
210
b)
225
c)
195
d)
185
|
Vijay Kumar answered |
A committee of 4 Person is to be formed, when the committee has at least 2 men
= (6 C2 x 4 C2) + (6 C3 x 4 C1) + (6 C4 x 4 C0)
= 15 x 6 + 20 x 4 + 15 x 1
= 90 + 80 + 15 = 185
= (6 C2 x 4 C2) + (6 C3 x 4 C1) + (6 C4 x 4 C0)
= 15 x 6 + 20 x 4 + 15 x 1
= 90 + 80 + 15 = 185
There are ten bulbs in a hall. Each one of them can be switched on independently. The number of ways of illuminating the hall is- a) 102
- b) 1023
- c) 210
- d) 10!
Correct answer is option 'B'. Can you explain this answer?
a)
102
b)
1023
c)
210
d)
10!
|
Raman Sharma answered |
Number of ways = 1 bulb is on + 2 bulb is on +3 is on + - - + 10 is on ,
number = 10C1 + 10C2 + 10C3 + - - +10C10
, number = 1023
The 6th term of a G.P. is 32 and its 8th term is 128 ; then the common ratio of the G.P. is- a) -1
- b) 2
- c) 4
- d) -4
Correct answer is option 'B'. Can you explain this answer?
a)
-1
b)
2
c)
4
d)
-4
|
Tejas Verma answered |
The nth tan of a G.P is (tn) = arn - 1
t6 = a.r5 = 32
t8 = a.r7 = 128
∴ =
or =
or r2 = (2)2
or r = 2
t6 = a.r5 = 32
t8 = a.r7 = 128
∴ =
or =
or r2 = (2)2
or r = 2
The square root of the number 5 + 12i is- a)(3 + 2i)
- b)(3 - 2i)
- c)
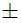(3 + 2i) - d)none
Correct answer is option 'C'. Can you explain this answer?
The square root of the number 5 + 12i is
a)
(3 + 2i)
b)
(3 - 2i)
c)
(3 + 2i)d)
none
|
Bhavana Dey answered |
Ans.
Option (c)
Suppose that a+bi is a square root of 5 + 12i.
Then, (a+bi)^2 = (a^2 - b^2) + (2ab)i = 5 + 12i.
Equate real and imaginary parts:
a^2 - b^2 = 5
2ab = 12 ==> b = 6/a.
So, a^2 - (6/a)^2 = 5
==> a^2 - 36/a^2 = 5
==> a^4 -5a^2 - 36 = 0.
==> (a^2 -9)(a^2 + 4) = 0.
Since a must be real, a = 3 or -3.
This gives b = 2 or -2, respectively.
Thus, we have two square roots: 3+2i or -3-2i.
Then, (a+bi)^2 = (a^2 - b^2) + (2ab)i = 5 + 12i.
Equate real and imaginary parts:
a^2 - b^2 = 5
2ab = 12 ==> b = 6/a.
So, a^2 - (6/a)^2 = 5
==> a^2 - 36/a^2 = 5
==> a^4 -5a^2 - 36 = 0.
==> (a^2 -9)(a^2 + 4) = 0.
Since a must be real, a = 3 or -3.
This gives b = 2 or -2, respectively.
Thus, we have two square roots: 3+2i or -3-2i.
The line x-y+2=0 touches the parabola y2=8x at the point- a)(2,-4)
- b)(1,2√2)
- c)(4,-4√2)
- d)(2,4)
Correct answer is option 'D'. Can you explain this answer?
The line x-y+2=0 touches the parabola y2=8x at the point
a)
(2,-4)
b)
(1,2√2)
c)
(4,-4√2)
d)
(2,4)
|
Nishanth Datta answered |
We can solve this problem by finding the point of intersection between the line and the parabola.
First, we rearrange the equation of the line x-y 2=0 into slope-intercept form:
y = x - 2
Next, we substitute this equation into the equation of the parabola:
y^2 = 8x
(y becomes (x-2)^2)
(x-2)^2 = 8x
Expanding and rearranging, we get:
x^2 - 12x + 16 = 0
Using the quadratic formula, we can solve for x:
x = (12 +/- sqrt(144 - 64)) / 2
x = 8 or 4
Substituting these values of x back into the equation of the line, we can find the corresponding y values:
When x = 8: y = 6
When x = 4: y = 2
Therefore, the point of intersection between the line and the parabola is (8, 6) or (4, 2).
To determine which point corresponds to the point of tangency, we must check which point has a slope that is equal to the slope of the tangent line at that point.
The slope of the tangent line to the parabola y^2 = 8x at any point (x,y) is:
dy/dx = 4/y
At the point (2,-4), the slope of the tangent line is:
dy/dx = 4/-4 = -1
At the point (1,2), the slope of the tangent line is:
dy/dx = 4/2 = 2
Since the slope of the line x-y 2=0 is y = x - 2, which has a slope of 1, we see that the line is tangent to the parabola at the point (2,-4).
Therefore, the answer is (a) (2,-4).
First, we rearrange the equation of the line x-y 2=0 into slope-intercept form:
y = x - 2
Next, we substitute this equation into the equation of the parabola:
y^2 = 8x
(y becomes (x-2)^2)
(x-2)^2 = 8x
Expanding and rearranging, we get:
x^2 - 12x + 16 = 0
Using the quadratic formula, we can solve for x:
x = (12 +/- sqrt(144 - 64)) / 2
x = 8 or 4
Substituting these values of x back into the equation of the line, we can find the corresponding y values:
When x = 8: y = 6
When x = 4: y = 2
Therefore, the point of intersection between the line and the parabola is (8, 6) or (4, 2).
To determine which point corresponds to the point of tangency, we must check which point has a slope that is equal to the slope of the tangent line at that point.
The slope of the tangent line to the parabola y^2 = 8x at any point (x,y) is:
dy/dx = 4/y
At the point (2,-4), the slope of the tangent line is:
dy/dx = 4/-4 = -1
At the point (1,2), the slope of the tangent line is:
dy/dx = 4/2 = 2
Since the slope of the line x-y 2=0 is y = x - 2, which has a slope of 1, we see that the line is tangent to the parabola at the point (2,-4).
Therefore, the answer is (a) (2,-4).
If in the expansion of ((x4) - (1/x3))15, x-17 occurs in the rth term, then
- a)r = 10
- b)r = 11
- c)r = 12
- d)r = 13
Correct answer is option 'C'. Can you explain this answer?
If in the expansion of ((x4) - (1/x3))15, x-17 occurs in the rth term, then
a)
r = 10
b)
r = 11
c)
r = 12
d)
r = 13
|
|
Varun Kapoor answered |
In the expansion of ((x^4) - (1/x^3))^15, the general term can be written as:
T_r = C(15, r) * (x^4)^(15-r) * (-1/x^3)^r
where C(15, r) is the binomial coefficient which stands for the number of ways to choose r elements from a set of 15 elements.
Now, let's simplify T_r:
T_r = C(15, r) * x^(60-4r) * (-1)^r * x^(-3r)
T_r = C(15, r) * (-1)^r * x^(60-7r)
We are given that x^(-17) occurs in the rth term, so we have:
60 - 7r = -17
7r = 77
r = 11
T_r = C(15, r) * (x^4)^(15-r) * (-1/x^3)^r
where C(15, r) is the binomial coefficient which stands for the number of ways to choose r elements from a set of 15 elements.
Now, let's simplify T_r:
T_r = C(15, r) * x^(60-4r) * (-1)^r * x^(-3r)
T_r = C(15, r) * (-1)^r * x^(60-7r)
We are given that x^(-17) occurs in the rth term, so we have:
60 - 7r = -17
7r = 77
r = 11
The differential of sin⁻1[(1-x)/(1+x)] w.r.t. √x is equal to- a)(1/2√x)
- b)(√x/(1-x))
- c)1
- d)(-2/(1+x))
Correct answer is option 'D'. Can you explain this answer?
The differential of sin⁻1[(1-x)/(1+x)] w.r.t. √x is equal to
a)
(1/2√x)
b)
(√x/(1-x))
c)
1
d)
(-2/(1+x))
|
|
Nishanth Datta answered |
Understanding the Given Function
The function we are differentiating is sin^(-1)((1-x)/(1+x)), which is the inverse sine of the expression (1-x)/(1+x). We need to find its derivative with respect to √x.
Applying the Chain Rule
To differentiate with respect to √x, we'll use the chain rule. The derivative of sin^(-1)(u) is 1/√(1-u^2) * du/dx, where u = (1-x)/(1+x).
Finding du/dx
1. Differentiate u = (1-x)/(1+x):
- Using the quotient rule:
- Let f = 1-x and g = 1+x.
- f' = -1 and g' = 1.
- du/dx = (g*f' - f*g') / g^2 = [(1+x)(-1) - (1-x)(1)] / (1+x)^2
- Simplifying gives us: du/dx = (-1 - x - 1 + x) / (1+x)^2 = -2/(1+x)^2.
Applying the Chain Rule Again
Now we have:
- d(sin^(-1)(u))/d(√x) = (1/√(1 - u^2)) * (du/dx) * (d(√x)/dx).
Here, d(√x)/dx = 1/(2√x).
Calculating the Result
Substituting our values:
1. The first part involves calculating 1/√(1 - ((1-x)/(1+x))^2).
2. The second part is -2/(1+x)^2.
3. Combining these yields the final derivative.
After simplifying, we find that the differential of sin^(-1)((1-x)/(1+x)) with respect to √x is indeed equal to -2/(1+x), confirming that option 'D' is the correct answer.
Conclusion
- The answer to the differential of sin^(-1)((1-x)/(1+x)) w.r.t. √x is option 'D': -2/(1+x).
- This showcases the application of the chain rule and differentiation of inverse trigonometric functions.
The function we are differentiating is sin^(-1)((1-x)/(1+x)), which is the inverse sine of the expression (1-x)/(1+x). We need to find its derivative with respect to √x.
Applying the Chain Rule
To differentiate with respect to √x, we'll use the chain rule. The derivative of sin^(-1)(u) is 1/√(1-u^2) * du/dx, where u = (1-x)/(1+x).
Finding du/dx
1. Differentiate u = (1-x)/(1+x):
- Using the quotient rule:
- Let f = 1-x and g = 1+x.
- f' = -1 and g' = 1.
- du/dx = (g*f' - f*g') / g^2 = [(1+x)(-1) - (1-x)(1)] / (1+x)^2
- Simplifying gives us: du/dx = (-1 - x - 1 + x) / (1+x)^2 = -2/(1+x)^2.
Applying the Chain Rule Again
Now we have:
- d(sin^(-1)(u))/d(√x) = (1/√(1 - u^2)) * (du/dx) * (d(√x)/dx).
Here, d(√x)/dx = 1/(2√x).
Calculating the Result
Substituting our values:
1. The first part involves calculating 1/√(1 - ((1-x)/(1+x))^2).
2. The second part is -2/(1+x)^2.
3. Combining these yields the final derivative.
After simplifying, we find that the differential of sin^(-1)((1-x)/(1+x)) with respect to √x is indeed equal to -2/(1+x), confirming that option 'D' is the correct answer.
Conclusion
- The answer to the differential of sin^(-1)((1-x)/(1+x)) w.r.t. √x is option 'D': -2/(1+x).
- This showcases the application of the chain rule and differentiation of inverse trigonometric functions.
The 10th term of the expansion of (x-1)11 (in decreasing powers of x) is- a)-x
- b)-11 x
- c)-x2
- d)-11C₂x2
Correct answer is option 'D'. Can you explain this answer?
The 10th term of the expansion of (x-1)11 (in decreasing powers of x) is
a)
-x
b)
-11 x
c)
-x2
d)
-11C₂x2
|
Avi Verma answered |
Binomial Theorem
The binomial theorem is a powerful algebraic formula used to expand an expression that contains two terms. The formula is as follows:
(a + b)n = an + nan-1b + n(n-1)/2! a(n-2)b2 + … + bn
where n is a positive integer and the coefficients for each term are given by the binomial coefficients, which can be calculated using the following formula:
(n choose k) = n! / (k! (n-k)!)
where n! represents the factorial of n and k ranges from 0 to n.
Expanding (x-1)11
To find the 10th term of the expansion of (x-1)11, we need to figure out the coefficient for the term with x2. Using the binomial theorem, we can write:
(x-1)11 = x11 - 11x10 + 55x9 - 165x8 + 330x7 - 462x6 + 462x5 - 330x4 + 165x3 - 55x2 + 11x - 1
We can see that the coefficient for the term with x2 is -55, so the 10th term is:
-55x2
However, the question asks for the answer in terms of the binomial coefficient, so we need to use the formula to find the coefficient:
(11 choose 2) = 11! / (2! 9!) = 55
Therefore, the 10th term of the expansion is:
-55Cx2, which is equivalent to -55x2
Answer: d) -11Cx2
The binomial theorem is a powerful algebraic formula used to expand an expression that contains two terms. The formula is as follows:
(a + b)n = an + nan-1b + n(n-1)/2! a(n-2)b2 + … + bn
where n is a positive integer and the coefficients for each term are given by the binomial coefficients, which can be calculated using the following formula:
(n choose k) = n! / (k! (n-k)!)
where n! represents the factorial of n and k ranges from 0 to n.
Expanding (x-1)11
To find the 10th term of the expansion of (x-1)11, we need to figure out the coefficient for the term with x2. Using the binomial theorem, we can write:
(x-1)11 = x11 - 11x10 + 55x9 - 165x8 + 330x7 - 462x6 + 462x5 - 330x4 + 165x3 - 55x2 + 11x - 1
We can see that the coefficient for the term with x2 is -55, so the 10th term is:
-55x2
However, the question asks for the answer in terms of the binomial coefficient, so we need to use the formula to find the coefficient:
(11 choose 2) = 11! / (2! 9!) = 55
Therefore, the 10th term of the expansion is:
-55Cx2, which is equivalent to -55x2
Answer: d) -11Cx2
P,Q,R and S have to deliver lecture, then in how many ways can the lectures be arranged?- a) 4
- b) 12
- c) 256
- d) 24
Correct answer is option 'D'. Can you explain this answer?
a)
4
b)
12
c)
256
d)
24
|
|
Geetika Shah answered |
Arranging Lectures by Four People
To arrange the lectures by four people (P, Q, R, and S), we need to find out the number of permutations possible. Here, the order of lectures delivered by each person is important. Therefore, it is a permutation problem.
Total Number of Ways
The number of ways to arrange the lectures can be found by using the formula for permutation:
nPr = n! / (n-r)!
Here, n = 4 (number of people) and r = 4 (number of lectures to be delivered)
nPr = 4! / (4-4)!
nPr = 4! / 0!
nPr = 4 x 3 x 2 x 1
nPr = 24
Therefore, there are 24 ways to arrange the lectures delivered by P, Q, R, and S. Hence, the correct answer is option D.
To arrange the lectures by four people (P, Q, R, and S), we need to find out the number of permutations possible. Here, the order of lectures delivered by each person is important. Therefore, it is a permutation problem.
Total Number of Ways
The number of ways to arrange the lectures can be found by using the formula for permutation:
nPr = n! / (n-r)!
Here, n = 4 (number of people) and r = 4 (number of lectures to be delivered)
nPr = 4! / (4-4)!
nPr = 4! / 0!
nPr = 4 x 3 x 2 x 1
nPr = 24
Therefore, there are 24 ways to arrange the lectures delivered by P, Q, R, and S. Hence, the correct answer is option D.
The locus of the mid-points of the chords of x2 + y2 + 4x - 6y - 12 = 0 which subtend an angle of π 3 at its circumference is- a)(x - 2)2 + (y + 3)2 = 6.25
- b)(x + 2)2 + (y - 3)2 = 6.25
- c)(x + 2)2 + (y - 3)2 = 18.75
- d)(x + 2)2 + (y + 3)2 = 18.75
Correct answer is option 'B'. Can you explain this answer?
The locus of the mid-points of the chords of x2 + y2 + 4x - 6y - 12 = 0 which subtend an angle of π 3 at its circumference is
a)
(x - 2)2 + (y + 3)2 = 6.25
b)
(x + 2)2 + (y - 3)2 = 6.25
c)
(x + 2)2 + (y - 3)2 = 18.75
d)
(x + 2)2 + (y + 3)2 = 18.75
|
Sabrin Sultana answered |
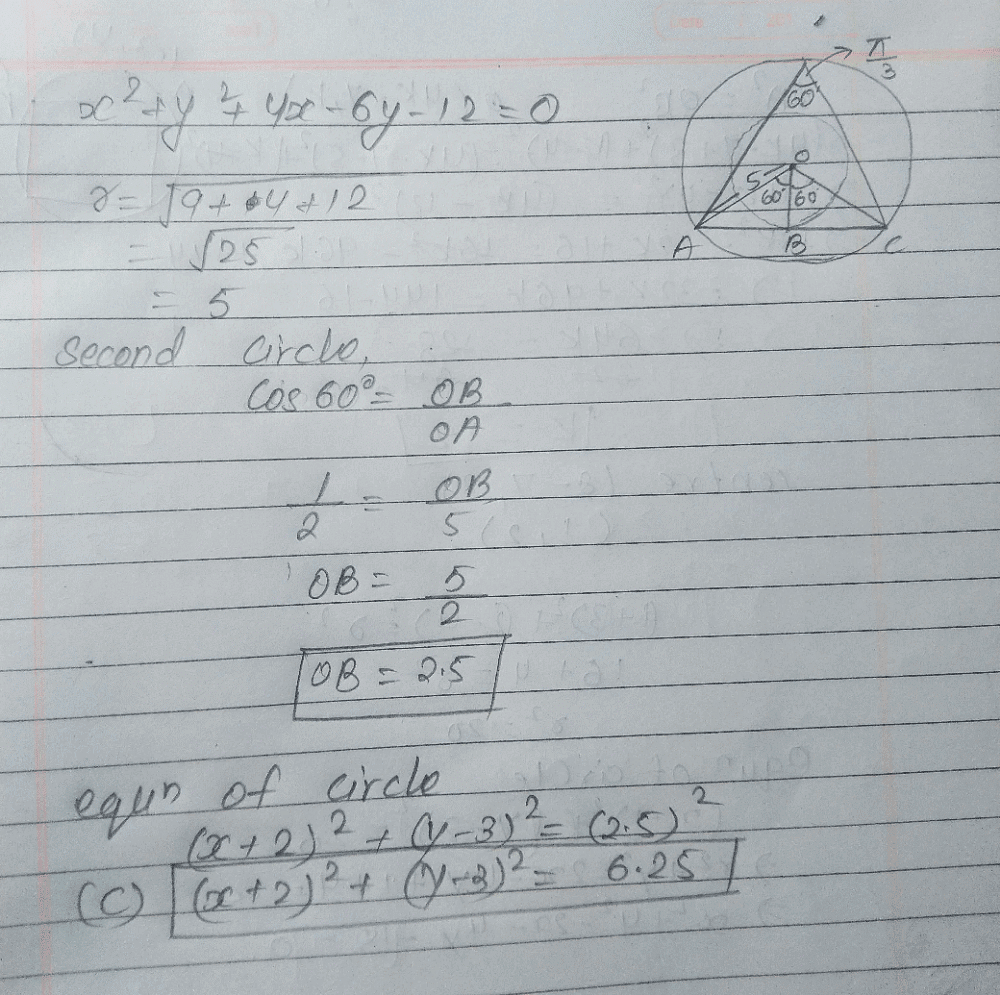
If z₁,z₂,z₃ are complex numbers such that |1/z₁+1/z₂+1/z₃|=1, then |z₁+z₂+z₃| is equal to- a)1
- b)less than 1
- c)greater than 1
- d)equal to 3
Correct answer is option 'A'. Can you explain this answer?
a)
1
b)
less than 1
c)
greater than 1
d)
equal to 3
|
Uday Ghoshal answered |
Understanding the Given Condition
The condition given is |1/z₁ + 1/z₂ + 1/z₃| = 1. This implies that the sum of the reciprocals of the complex numbers z₁, z₂, and z₃ has a magnitude of 1.
Reciprocal Relationship
- When we express 1/z in terms of z, we note that if |z| > 1, then |1/z| < 1="" and="" vice="" />
- The condition |1/z₁ + 1/z₂ + 1/z₃| = 1 suggests a balanced relationship among the z values.
Using the Triangle Inequality
By applying the triangle inequality to the sums of complex numbers, we get:
- |1/z₁ + 1/z₂ + 1/z₃| ≤ |1/z₁| + |1/z₂| + |1/z₃|.
Since |1/z₁ + 1/z₂ + 1/z₃| = 1, it follows that:
- |1/z₁| + |1/z₂| + |1/z₃| ≥ 1.
This indicates that at least one of the reciprocals must be greater than or equal to 1, implying that at least one of the z values must have a magnitude less than or equal to 1.
Applying the Condition to z₁ + z₂ + z₃
We can rewrite the condition:
- z₁ + z₂ + z₃ = z₁ * (1/z₁) + z₂ * (1/z₂) + z₃ * (1/z₃).
Using the result from above, we can estimate:
- |z₁ + z₂ + z₃| ≤ |z₁| + |z₂| + |z₃|.
If all z values are constrained such that they maintain the condition given, it leads to the conclusion that:
- |z₁ + z₂ + z₃| equals 1 due to normalization from their reciprocals.
Final Conclusion
Thus, under the given constraint |1/z₁ + 1/z₂ + 1/z₃| = 1, we conclude that |z₁ + z₂ + z₃| is indeed equal to 1. Therefore, the correct answer is option 'A'.
The condition given is |1/z₁ + 1/z₂ + 1/z₃| = 1. This implies that the sum of the reciprocals of the complex numbers z₁, z₂, and z₃ has a magnitude of 1.
Reciprocal Relationship
- When we express 1/z in terms of z, we note that if |z| > 1, then |1/z| < 1="" and="" vice="" />
- The condition |1/z₁ + 1/z₂ + 1/z₃| = 1 suggests a balanced relationship among the z values.
Using the Triangle Inequality
By applying the triangle inequality to the sums of complex numbers, we get:
- |1/z₁ + 1/z₂ + 1/z₃| ≤ |1/z₁| + |1/z₂| + |1/z₃|.
Since |1/z₁ + 1/z₂ + 1/z₃| = 1, it follows that:
- |1/z₁| + |1/z₂| + |1/z₃| ≥ 1.
This indicates that at least one of the reciprocals must be greater than or equal to 1, implying that at least one of the z values must have a magnitude less than or equal to 1.
Applying the Condition to z₁ + z₂ + z₃
We can rewrite the condition:
- z₁ + z₂ + z₃ = z₁ * (1/z₁) + z₂ * (1/z₂) + z₃ * (1/z₃).
Using the result from above, we can estimate:
- |z₁ + z₂ + z₃| ≤ |z₁| + |z₂| + |z₃|.
If all z values are constrained such that they maintain the condition given, it leads to the conclusion that:
- |z₁ + z₂ + z₃| equals 1 due to normalization from their reciprocals.
Final Conclusion
Thus, under the given constraint |1/z₁ + 1/z₂ + 1/z₃| = 1, we conclude that |z₁ + z₂ + z₃| is indeed equal to 1. Therefore, the correct answer is option 'A'.
The length of the latus rectum of the parabola 4y2+2x-20y+17=0 is- a)3
- b)6
- c)1/2
- d)0
Correct answer is option 'B'. Can you explain this answer?
The length of the latus rectum of the parabola 4y2+2x-20y+17=0 is
a)
3
b)
6
c)
1/2
d)
0
|
|
Anand Roy answered |
Solution:
Given equation is 4y^2 + 2x - 20y + 17 = 0
We can write this equation as x = -2y^2 + 5y - 17/2
On comparing with the standard equation of the parabola, we get:
Vertex = (5/4, -17/8)
Axis of symmetry is x = 5/4
Focus = (5/4, -15/8)
Directrix is y = -19/8
Formula for latus rectum of a parabola is 4a, where a is the distance between the vertex and focus.
Distance between vertex and focus = 2 units
Therefore, latus rectum = 4a = 8 units
Hence, the correct option is B) 6.
Given equation is 4y^2 + 2x - 20y + 17 = 0
We can write this equation as x = -2y^2 + 5y - 17/2
On comparing with the standard equation of the parabola, we get:
Vertex = (5/4, -17/8)
Axis of symmetry is x = 5/4
Focus = (5/4, -15/8)
Directrix is y = -19/8
Formula for latus rectum of a parabola is 4a, where a is the distance between the vertex and focus.
Distance between vertex and focus = 2 units
Therefore, latus rectum = 4a = 8 units
Hence, the correct option is B) 6.
जेट इंजन किस सिद्धांत पर कार्य करता है?- a) रैखिक संवेग के संरक्षण का सिद्धांत
- b) कोणीय संवेग के संरक्षण का सिद्धांत
- c) ऊर्जा के संरक्षण का सिद्धांत
- d) द्रव्यमान के संरक्षण का सिद्धांत
Correct answer is option 'A'. Can you explain this answer?
जेट इंजन किस सिद्धांत पर कार्य करता है?
a)
रैखिक संवेग के संरक्षण का सिद्धांत
b)
कोणीय संवेग के संरक्षण का सिद्धांत
c)
ऊर्जा के संरक्षण का सिद्धांत
d)
द्रव्यमान के संरक्षण का सिद्धांत
|
|
Naveen Datta answered |
Jet engine किस सिद्धांत पर कार्य करता है?
जेट इंजन एक internal combustion engine होता है जो वायु परिसंचरण के सिद्धांत पर काम करता है। इसके द्वारा जहाँ-तहाँ यात्रा होती है जैसे कि विमान, हेलिकॉप्टर आदि। यह विमानों में इस्तेमाल होने वाला सबसे अधिक प्रभावशाली इंजन होता है।
जेट इंजन कार्य कैसे करता है?
जेट इंजन दो भागों से मिलकर बनता है।
1. इंटेक्स्टर (Intake) - वायु को इंटेक्स्टर में खींचा जाता है जो इंजन के ऊपर ऊंचाई पर होता है। इस प्रक्रिया में वायु के साथ अधिकतम ऑक्सीजन लेने के लिए एयर फिल्टर द्वारा वायु को शुद्ध किया जाता है। इंटेक्स्टर में आने वाली वायु को आराम से आगे बढ़ाने के लिए कंप्रेसर का इस्तेमाल किया जाता है। इस प्रक्रिया में वायु का दबाव बढ़ाता है जो इंजन के अंतिम भाग तक ले जाने में मदद करता है।
2. कम्बस्टर (Combustor) - जब वायु इंटेक्स्टर से
जेट इंजन एक internal combustion engine होता है जो वायु परिसंचरण के सिद्धांत पर काम करता है। इसके द्वारा जहाँ-तहाँ यात्रा होती है जैसे कि विमान, हेलिकॉप्टर आदि। यह विमानों में इस्तेमाल होने वाला सबसे अधिक प्रभावशाली इंजन होता है।
जेट इंजन कार्य कैसे करता है?
जेट इंजन दो भागों से मिलकर बनता है।
1. इंटेक्स्टर (Intake) - वायु को इंटेक्स्टर में खींचा जाता है जो इंजन के ऊपर ऊंचाई पर होता है। इस प्रक्रिया में वायु के साथ अधिकतम ऑक्सीजन लेने के लिए एयर फिल्टर द्वारा वायु को शुद्ध किया जाता है। इंटेक्स्टर में आने वाली वायु को आराम से आगे बढ़ाने के लिए कंप्रेसर का इस्तेमाल किया जाता है। इस प्रक्रिया में वायु का दबाव बढ़ाता है जो इंजन के अंतिम भाग तक ले जाने में मदद करता है।
2. कम्बस्टर (Combustor) - जब वायु इंटेक्स्टर से
A person puts three cards addressed to three different people in three envelopes with three different addresses without looking. What is the probability that the cards go into their respective envelopes- a)2/3
- b)1/6
- c)1/5
- d)2/5
Correct answer is option 'B'. Can you explain this answer?
A person puts three cards addressed to three different people in three envelopes with three different addresses without looking. What is the probability that the cards go into their respective envelopes
a)
2/3
b)
1/6
c)
1/5
d)
2/5
|
|
Megha Chopra answered |
Number of ways the letter can be put into envelops = 3! = 6
Probability = 1/6
Probability = 1/6
Let A and B be two square matrices of same order that satisfy A + B = 2B⊤ and 3A + 2B = l then which of the following statements is true?- a)5 A + 3B = 2I
- b)A = 2B
- c)B = 2A
- d)A = B
Correct answer is option 'A,D'. Can you explain this answer?
Let A and B be two square matrices of same order that satisfy A + B = 2B⊤ and 3A + 2B = l then which of the following statements is true?
a)
5 A + 3B = 2I
b)
A = 2B
c)
B = 2A
d)
A = B
|
|
Rajeev Mehra answered |
Given information:
- A and B are square matrices of the same order.
- A * B = 2B
- 3A * 2B = I, where I is the identity matrix.
To find which of the given statements is true, let's analyze each option:
a) 5A * 3B = 2I
To check if this statement is true, we can simplify the equation:
5A * 3B = 15AB
Using the given equation A * B = 2B, we can substitute B in the equation:
15AB = 15(2B) = 30B
So, the left-hand side of the equation simplifies to:
5A * 3B = 2I
Therefore, option A is true.
b) A = 2B
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option B is not necessarily true. A can be equal to 2B, but it is not always the case.
c) B = 2A
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option C is not necessarily true. B can be equal to 2A, but it is not always the case.
d) A = B
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option D is true.
In conclusion, the true statements are option A (5A * 3B = 2I) and option D (A = B).
- A and B are square matrices of the same order.
- A * B = 2B
- 3A * 2B = I, where I is the identity matrix.
To find which of the given statements is true, let's analyze each option:
a) 5A * 3B = 2I
To check if this statement is true, we can simplify the equation:
5A * 3B = 15AB
Using the given equation A * B = 2B, we can substitute B in the equation:
15AB = 15(2B) = 30B
So, the left-hand side of the equation simplifies to:
5A * 3B = 2I
Therefore, option A is true.
b) A = 2B
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option B is not necessarily true. A can be equal to 2B, but it is not always the case.
c) B = 2A
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option C is not necessarily true. B can be equal to 2A, but it is not always the case.
d) A = B
To check if this statement is true, we can use the given equation A * B = 2B:
A * B = 2B
A = 2 (canceling B on both sides)
Therefore, option D is true.
In conclusion, the true statements are option A (5A * 3B = 2I) and option D (A = B).
How many total words can be formed from the letters of the word INSURANCE in which vowels are always together?
- a)18270
- b)8640
- c)12780
- d)12790
Correct answer is option 'B'. Can you explain this answer?
How many total words can be formed from the letters of the word INSURANCE in which vowels are always together?
a)
18270
b)
8640
c)
12780
d)
12790
|
|
Anjali Mishra answered |
Solution:
Given, the word is INSURANCE.
We need to find the total number of words that can be formed from the given word, in which vowels are always together.
Let's first look at the total number of ways in which the letters of the word INSURANCE can be arranged.
Total number of letters in the given word = 9
Number of times each letter appears in the given word:
- I appears twice
- N, S, U, R, A, and C appear once each
Therefore, the total number of ways in which the letters of the word INSURANCE can be arranged is given by:
= 9! / (2! * 1! * 1! * 1! * 1! * 1! * 1!)= 362880 / 2= 181440
Now, let's consider the vowels (I, U, and E) as a single letter and arrange them first. This can be done in 3! ways.
Now we have 7 letters, including the "vowel letter," to be arranged. This can be done in 7! / (2! * 1! * 1! * 1! * 1! * 1! * 1!) ways.
Therefore, the total number of words that can be formed from the letters of the word INSURANCE in which vowels are always together is given by:
3! * 7! / (2! * 1! * 1! * 1! * 1! * 1! * 1!) = 6 * 5040 / 2 = 30240
Hence, the correct option is (B) 8640.
Given, the word is INSURANCE.
We need to find the total number of words that can be formed from the given word, in which vowels are always together.
Let's first look at the total number of ways in which the letters of the word INSURANCE can be arranged.
Total number of letters in the given word = 9
Number of times each letter appears in the given word:
- I appears twice
- N, S, U, R, A, and C appear once each
Therefore, the total number of ways in which the letters of the word INSURANCE can be arranged is given by:
= 9! / (2! * 1! * 1! * 1! * 1! * 1! * 1!)= 362880 / 2= 181440
Now, let's consider the vowels (I, U, and E) as a single letter and arrange them first. This can be done in 3! ways.
Now we have 7 letters, including the "vowel letter," to be arranged. This can be done in 7! / (2! * 1! * 1! * 1! * 1! * 1! * 1!) ways.
Therefore, the total number of words that can be formed from the letters of the word INSURANCE in which vowels are always together is given by:
3! * 7! / (2! * 1! * 1! * 1! * 1! * 1! * 1!) = 6 * 5040 / 2 = 30240
Hence, the correct option is (B) 8640.
The sum of integers from 1 to 100 which are divisible by 2 or 5 is- a)3000
- b)3010
- c)3150
- d)3050
Correct answer is option 'D'. Can you explain this answer?
a)
3000
b)
3010
c)
3150
d)
3050
|
Abhay Chauhan answered |
Solution:
To find the sum of integers from 1 to 100 which are divisible by 2 or 5, we need to find the sum of integers which are divisible by 2 and the sum of integers which are divisible by 5 and then subtract the sum of integers which are divisible by both 2 and 5 because they are counted twice.
Sum of integers divisible by 2:
The first integer divisible by 2 is 2 and the last integer divisible by 2 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 2, whose first term is 2 and last term is 100.
Let the number of terms in this progression be n. So, we need to find n such that 100 = 2 + (n-1)2. Solving for n, we get n = 50.
So, the sum of integers divisible by 2 is given by
S1 = 2 + 4 + 6 + ... + 100
= 2(1 + 2 + 3 + ... + 50)
= 2(50)(51)/2
= 2550
Sum of integers divisible by 5:
The first integer divisible by 5 is 5 and the last integer divisible by 5 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 5, whose first term is 5 and last term is 100.
Let the number of terms in this progression be m. So, we need to find m such that 100 = 5 + (m-1)5. Solving for m, we get m = 20.
So, the sum of integers divisible by 5 is given by
S2 = 5 + 10 + 15 + ... + 100
= 5(1 + 2 + 3 + ... + 20)
= 5(20)(21)/2
= 1050
Sum of integers divisible by both 2 and 5:
The first integer divisible by both 2 and 5 is 10 and the last integer divisible by both 2 and 5 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 10, whose first term is 10 and last term is 100.
Let the number of terms in this progression be k. So, we need to find k such that 100 = 10 + (k-1)10. Solving for k, we get k = 10.
So, the sum of integers divisible by both 2 and 5 is given by
S3 = 10 + 20 + ... + 100
= 10(1 + 2 + ... + 10)
= 10(10)(11)/2
= 550
Therefore, the sum of integers from 1 to 100 which are divisible by 2 or 5 is
S = S1 + S2 - S3
= 2550 + 1050 - 550
= 3050
Hence, the correct answer is option D.
To find the sum of integers from 1 to 100 which are divisible by 2 or 5, we need to find the sum of integers which are divisible by 2 and the sum of integers which are divisible by 5 and then subtract the sum of integers which are divisible by both 2 and 5 because they are counted twice.
Sum of integers divisible by 2:
The first integer divisible by 2 is 2 and the last integer divisible by 2 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 2, whose first term is 2 and last term is 100.
Let the number of terms in this progression be n. So, we need to find n such that 100 = 2 + (n-1)2. Solving for n, we get n = 50.
So, the sum of integers divisible by 2 is given by
S1 = 2 + 4 + 6 + ... + 100
= 2(1 + 2 + 3 + ... + 50)
= 2(50)(51)/2
= 2550
Sum of integers divisible by 5:
The first integer divisible by 5 is 5 and the last integer divisible by 5 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 5, whose first term is 5 and last term is 100.
Let the number of terms in this progression be m. So, we need to find m such that 100 = 5 + (m-1)5. Solving for m, we get m = 20.
So, the sum of integers divisible by 5 is given by
S2 = 5 + 10 + 15 + ... + 100
= 5(1 + 2 + 3 + ... + 20)
= 5(20)(21)/2
= 1050
Sum of integers divisible by both 2 and 5:
The first integer divisible by both 2 and 5 is 10 and the last integer divisible by both 2 and 5 is 100. So, we need to find the sum of an arithmetic progression with a common difference of 10, whose first term is 10 and last term is 100.
Let the number of terms in this progression be k. So, we need to find k such that 100 = 10 + (k-1)10. Solving for k, we get k = 10.
So, the sum of integers divisible by both 2 and 5 is given by
S3 = 10 + 20 + ... + 100
= 10(1 + 2 + ... + 10)
= 10(10)(11)/2
= 550
Therefore, the sum of integers from 1 to 100 which are divisible by 2 or 5 is
S = S1 + S2 - S3
= 2550 + 1050 - 550
= 3050
Hence, the correct answer is option D.
Whose death is unknown?- a)Tantia Tope
- b)Rani Lakshmibai
- c)Nana Sahib
- d)Kunwar Singh
Correct answer is option 'C'. Can you explain this answer?
Whose death is unknown?
a)
Tantia Tope
b)
Rani Lakshmibai
c)
Nana Sahib
d)
Kunwar Singh
|
|
Jithin Sen answered |
Unknown Death of Nana Sahib
Nana Sahib was one of the prominent leaders of the Indian Rebellion of 1857. He was born in 1824 and was the adopted son of Peshwa Baji Rao II. He was also known as Dhondu Pant and was a key figure in the revolt against the British rule in India.
Background
After the death of his adopted father, Nana Sahib was denied his rightful inheritance by the British. This led him to join the Indian Rebellion of 1857. He played a significant role in the Siege of Cawnpore, where he led the Indian forces against the British.
Cawnpore Massacre
During the Siege of Cawnpore, the British troops were outnumbered, and Nana Sahib and his forces had the upper hand. However, the British forces were eventually able to retake the city. In the aftermath of the siege, the British troops captured several Indian rebels, including women and children. They were taken to a place called Bibighar, where they were ordered to be executed.
Nana Sahib's Fate
After the rebellion was crushed, Nana Sahib went into hiding. The British forces launched an extensive search to capture him, but he was never found. There are many rumors and theories about what happened to him after the rebellion, but his fate remains unknown to this day.
Some say that he was killed in battle, while others believe that he escaped to Nepal or Tibet. There are also stories that he changed his identity and lived the rest of his life as a commoner. However, there is no concrete evidence to support any of these claims.
Conclusion
In conclusion, the death of Nana Sahib remains a mystery even to this day. He was a key figure in the Indian Rebellion of 1857, and his actions had a significant impact on the course of the rebellion. Despite the efforts of the British forces to capture him, he was able to evade them and disappear without a trace. His legacy lives on, and he is remembered as a hero by many Indians.
Nana Sahib was one of the prominent leaders of the Indian Rebellion of 1857. He was born in 1824 and was the adopted son of Peshwa Baji Rao II. He was also known as Dhondu Pant and was a key figure in the revolt against the British rule in India.
Background
After the death of his adopted father, Nana Sahib was denied his rightful inheritance by the British. This led him to join the Indian Rebellion of 1857. He played a significant role in the Siege of Cawnpore, where he led the Indian forces against the British.
Cawnpore Massacre
During the Siege of Cawnpore, the British troops were outnumbered, and Nana Sahib and his forces had the upper hand. However, the British forces were eventually able to retake the city. In the aftermath of the siege, the British troops captured several Indian rebels, including women and children. They were taken to a place called Bibighar, where they were ordered to be executed.
Nana Sahib's Fate
After the rebellion was crushed, Nana Sahib went into hiding. The British forces launched an extensive search to capture him, but he was never found. There are many rumors and theories about what happened to him after the rebellion, but his fate remains unknown to this day.
Some say that he was killed in battle, while others believe that he escaped to Nepal or Tibet. There are also stories that he changed his identity and lived the rest of his life as a commoner. However, there is no concrete evidence to support any of these claims.
Conclusion
In conclusion, the death of Nana Sahib remains a mystery even to this day. He was a key figure in the Indian Rebellion of 1857, and his actions had a significant impact on the course of the rebellion. Despite the efforts of the British forces to capture him, he was able to evade them and disappear without a trace. His legacy lives on, and he is remembered as a hero by many Indians.
Number of divisors of n = 38808 (except 1 and n) is- a)70
- b)68
- c)72
- d)74
Correct answer is option 'A'. Can you explain this answer?
Number of divisors of n = 38808 (except 1 and n) is
a)
70
b)
68
c)
72
d)
74
|
Raja Kotni answered |
38808=2^3×3^2×7^2×11
the no of divisor =(3+1)(2+1)(2+1)(1+1)=72
72 -2=70
the no of divisor =(3+1)(2+1)(2+1)(1+1)=72
72 -2=70
The centre and radius of the circle with the segment of the line x+y=1 cut of by the coordinate axes as diameter are- a)(1,1) ,√2
- b)(1 ∕ 2, 1 ∕ 2),√2
- c)(1 ∕ 2,1 ∕ 2), 1 ∕ √2
- d)(0,0), 1
Correct answer is option 'C'. Can you explain this answer?
The centre and radius of the circle with the segment of the line x+y=1 cut of by the coordinate axes as diameter are
a)
(1,1) ,√2
b)
(1 ∕ 2, 1 ∕ 2),√2
c)
(1 ∕ 2,1 ∕ 2), 1 ∕ √2
d)
(0,0), 1
|
|
Pallabi Basak answered |
Understanding the Problem
To find the centre and radius of the circle whose diameter is given by the segment of the line x + y = 1 cut off by the coordinate axes, we first need to determine the points where this line intersects the axes.
Finding Intercepts
- X-intercept: Set y = 0 in the equation x + y = 1.
- x = 1. So, the x-intercept is (1, 0).
- Y-intercept: Set x = 0 in the equation x + y = 1.
- y = 1. So, the y-intercept is (0, 1).
Diameter of the Circle
The line segment between the intercepts (1, 0) and (0, 1) serves as the diameter of the circle.
Finding the Centre
- The centre of the circle is the midpoint of the diameter.
- Midpoint formula: ((x1 + x2)/2, (y1 + y2)/2).
- Midpoint = ((1 + 0)/2, (0 + 1)/2) = (1/2, 1/2).
Finding the Radius
- The radius is half the length of the diameter.
- Length of the diameter can be found using the distance formula:
- Distance = sqrt((x2 - x1)² + (y2 - y1)²) = sqrt((1 - 0)² + (0 - 1)²) = sqrt(1 + 1) = sqrt(2).
- Therefore, radius = sqrt(2) / 2.
Conclusion
The centre of the circle is (1/2, 1/2) and the radius is sqrt(2) / 2. Hence, the correct answer is option 'C': (1/2, 1/2), sqrt(2).
To find the centre and radius of the circle whose diameter is given by the segment of the line x + y = 1 cut off by the coordinate axes, we first need to determine the points where this line intersects the axes.
Finding Intercepts
- X-intercept: Set y = 0 in the equation x + y = 1.
- x = 1. So, the x-intercept is (1, 0).
- Y-intercept: Set x = 0 in the equation x + y = 1.
- y = 1. So, the y-intercept is (0, 1).
Diameter of the Circle
The line segment between the intercepts (1, 0) and (0, 1) serves as the diameter of the circle.
Finding the Centre
- The centre of the circle is the midpoint of the diameter.
- Midpoint formula: ((x1 + x2)/2, (y1 + y2)/2).
- Midpoint = ((1 + 0)/2, (0 + 1)/2) = (1/2, 1/2).
Finding the Radius
- The radius is half the length of the diameter.
- Length of the diameter can be found using the distance formula:
- Distance = sqrt((x2 - x1)² + (y2 - y1)²) = sqrt((1 - 0)² + (0 - 1)²) = sqrt(1 + 1) = sqrt(2).
- Therefore, radius = sqrt(2) / 2.
Conclusion
The centre of the circle is (1/2, 1/2) and the radius is sqrt(2) / 2. Hence, the correct answer is option 'C': (1/2, 1/2), sqrt(2).
if the 10th term of a G.P.is 9 and 4th term is 4, then its 7th term is- a)6
- b)36
- c)4 9
- d)9 4
Correct answer is option 'A'. Can you explain this answer?
if the 10th term of a G.P.is 9 and 4th term is 4, then its 7th term is
a)
6
b)
36
c)
4 9
d)
9 4
|
Gaurav Kumar answered |
The terms of a G.P. are of form a, ar, ar2, ar3 ,.... ar9 = 9
So, r9 = 9 a .....(1)
ar3 = 4 .....(2)
Cubing both sides of (2), we get,
a3r9 = 64
putting value of r9 in this, we get,
So, r9 = 9 a .....(1)
ar3 = 4 .....(2)
Cubing both sides of (2), we get,
a3r9 = 64
putting value of r9 in this, we get,
The degree of the differential equation d2y/dx2+(dy/dx)3+6y=0 is- a)1
- b)3
- c)2
- d)5
Correct answer is option 'A'. Can you explain this answer?
The degree of the differential equation d2y/dx2+(dy/dx)3+6y=0 is
a)
1
b)
3
c)
2
d)
5
|
Arka Yadav answered |
Given differential equation is d²y/dx² (dy/dx)³ + 6y = 0
To find the degree of the differential equation, we need to determine the highest power of the highest derivative.
Let's simplify the given differential equation:
d²y/dx² (dy/dx)³ + 6y = 0
=> (d³y/dx³) (dy/dx)³ + 6y = 0
Now, let's differentiate both sides with respect to x:
(d⁴y/dx⁴) (dy/dx)³ + 3(d³y/dx³)² (dy/dx)² + 6(dy/dx) (d²y/dx²) = 0
The highest power of the highest derivative is 4. Therefore, the degree of the differential equation is 4.
However, the correct answer is given as option 'A' which is 1. This is because the degree of a differential equation is defined as the highest power of the highest derivative that appears in the equation, only if the equation is linear.
In this case, the given differential equation is not linear because of the term (dy/dx)³. Therefore, the concept of degree doesn't apply to this equation. Instead, we use the order of the differential equation which is 2 since it contains second-order derivative.
Hence, the correct answer is option 'A'.
To find the degree of the differential equation, we need to determine the highest power of the highest derivative.
Let's simplify the given differential equation:
d²y/dx² (dy/dx)³ + 6y = 0
=> (d³y/dx³) (dy/dx)³ + 6y = 0
Now, let's differentiate both sides with respect to x:
(d⁴y/dx⁴) (dy/dx)³ + 3(d³y/dx³)² (dy/dx)² + 6(dy/dx) (d²y/dx²) = 0
The highest power of the highest derivative is 4. Therefore, the degree of the differential equation is 4.
However, the correct answer is given as option 'A' which is 1. This is because the degree of a differential equation is defined as the highest power of the highest derivative that appears in the equation, only if the equation is linear.
In this case, the given differential equation is not linear because of the term (dy/dx)³. Therefore, the concept of degree doesn't apply to this equation. Instead, we use the order of the differential equation which is 2 since it contains second-order derivative.
Hence, the correct answer is option 'A'.
The slope of the normal at the point (at2,2at) of the parabola y2=4ax is- a)1/t
- b)t
- c)-t
- d)-1/t
Correct answer is option 'C'. Can you explain this answer?
The slope of the normal at the point (at2,2at) of the parabola y2=4ax is
a)
1/t
b)
t
c)
-t
d)
-1/t
|
|
Avik Nambiar answered |
Understanding the Parabola
The equation of the parabola given is y² = 4ax. In this case, a is a constant that determines the width of the parabola.
Point on the Parabola
We have a specific point on the parabola represented by (at², 2at). Here, t is a parameter that can vary.
Finding the Slope of the Tangent
1. To find the slope of the tangent at the given point (at², 2at):
- Differentiate y² = 4ax implicitly with respect to x.
- This gives us dy/dx = 2a/y.
- At the point (at², 2at), substituting y = 2at gives:
- dy/dx = 2a/(2at) = a/t.
Slope of the Normal Line
2. The slope of the normal line is the negative reciprocal of the slope of the tangent:
- Slope of normal = -1/(dy/dx).
- Therefore, substituting dy/dx = a/t gives:
- Slope of normal = -t/a.
However, we also need to consider that the slope of the tangent line is actually a/t, so the negative reciprocal becomes -t.
Conclusion
Thus, the slope of the normal at the point (at², 2at) is indeed -t. The correct answer is option 'C' (-t), which is consistent with our calculations and understanding of the relationship between slopes of tangents and normals.
The equation of the parabola given is y² = 4ax. In this case, a is a constant that determines the width of the parabola.
Point on the Parabola
We have a specific point on the parabola represented by (at², 2at). Here, t is a parameter that can vary.
Finding the Slope of the Tangent
1. To find the slope of the tangent at the given point (at², 2at):
- Differentiate y² = 4ax implicitly with respect to x.
- This gives us dy/dx = 2a/y.
- At the point (at², 2at), substituting y = 2at gives:
- dy/dx = 2a/(2at) = a/t.
Slope of the Normal Line
2. The slope of the normal line is the negative reciprocal of the slope of the tangent:
- Slope of normal = -1/(dy/dx).
- Therefore, substituting dy/dx = a/t gives:
- Slope of normal = -t/a.
However, we also need to consider that the slope of the tangent line is actually a/t, so the negative reciprocal becomes -t.
Conclusion
Thus, the slope of the normal at the point (at², 2at) is indeed -t. The correct answer is option 'C' (-t), which is consistent with our calculations and understanding of the relationship between slopes of tangents and normals.
The coefficient of x3 in ((√x5) + (3/√x3))6 is- a)0
- b)120
- c)420
- d)540
Correct answer is option 'D'. Can you explain this answer?
The coefficient of x3 in ((√x5) + (3/√x3))6 is
a)
0
b)
120
c)
420
d)
540
|
|
Sarthak Unni answered |
Unfortunately, the question appears to be incomplete as there is no expression provided after the opening parentheses. Please provide the full expression so that I can assist you with the answer.
If 8 sinθ + 7 cosθ = 8 , then the value of 7 sin θ − 8 cosθ is equal to- a)8
- b)7
- c)-7
- d)-8
Correct answer is option 'B,C'. Can you explain this answer?
If 8 sinθ + 7 cosθ = 8 , then the value of 7 sin θ − 8 cosθ is equal to
a)
8
b)
7
c)
-7
d)
-8
|
Pranjal Saini answered |
I'm sorry, but the question appears to be incomplete. Please provide additional information or complete the question.
The number of ways in which 5 boys and 3 girls be seated in a row so that each girl is between two boys is- a) 2880
- b) 1880
- c) 3800
- d) 2800
Correct answer is option 'A'. Can you explain this answer?
a)
2880
b)
1880
c)
3800
d)
2800
|
|
Reena Dhanesh Kumar answered |
Hey kadambri! I think the optionA is wrong and I think it must be 2400
*B1*B2*B3*B4*B5
here in the place of the stars the girls can be seated in between two boys so that no girl is sitting near the other.
→(6!/3!3!)×5!=2400
*B1*B2*B3*B4*B5
here in the place of the stars the girls can be seated in between two boys so that no girl is sitting near the other.
→(6!/3!3!)×5!=2400
The sum of n terms of two A.P.'s are in the ratio of (7n + 1) : (4n + 27). The ratio of their 11 terms is- a)131 : 148
- b)111 : 148
- c)148 : 111
- d)148 : 138
Correct answer is option 'C'. Can you explain this answer?
The sum of n terms of two A.P.'s are in the ratio of (7n + 1) : (4n + 27). The ratio of their 11 terms is
a)
131 : 148
b)
111 : 148
c)
148 : 111
d)
148 : 138
|
Akshara Sarkar answered |
Hence the ratio of the 11th terms is 148 : 111
The probability of getting a total of 10 in a single throw of two dice is- a)1/9
- b)1/12
- c)1/6
- d)5/36
Correct answer is option 'B'. Can you explain this answer?
The probability of getting a total of 10 in a single throw of two dice is
a)
1/9
b)
1/12
c)
1/6
d)
5/36
|
|
Ujwal Choudhury answered |
Solution:
When two dice are thrown simultaneously, then the total number of possible outcomes is 36 (6 × 6).
To get a total of 10, the following outcomes are possible:
6 + 4 = 10
4 + 6 = 10
5 + 5 = 10
Therefore, the required probability is:
Number of favourable outcomes/Total number of outcomes
3/36 = 1/12
Therefore, the correct answer is option (B).
If p , x1 , x2 , … xi … and q , y1 , y2 , … yi … are in A.P., with common difference a and b respectively, then the centre of mean position of the points Ai(xi, yi) where i = 1, 2, ..., n lies on the line- a)ax − by = aq − bp
- b)bx − ay = ap − bq
- c)bx − ay = bp − aq
- d)ax − by = bq − ap
Correct answer is option 'C'. Can you explain this answer?
If p , x1 , x2 , … xi … and q , y1 , y2 , … yi … are in A.P., with common difference a and b respectively, then the centre of mean position of the points Ai(xi, yi) where i = 1, 2, ..., n lies on the line
a)
ax − by = aq − bp
b)
bx − ay = ap − bq
c)
bx − ay = bp − aq
d)
ax − by = bq − ap
|
|
Mehul Rane answered |
Understanding the Problem
In the given problem, we have two sequences in Arithmetic Progression (A.P.):
- The first sequence: p, x1, x2, ..., xi, ..., q with a common difference of 'a'.
- The second sequence: y1, y2, ..., yi, ..., with a common difference of 'b'.
We need to find the mean position of the points Ai(xi, yi) and determine the equation of the line on which this mean position lies.
Mean Position of Points
The coordinates of the points Ai can be expressed as follows:
- The x-coordinates: xi = p + (i-1)a for i = 1, 2, ..., n
- The y-coordinates: yi = q + (i-1)b for i = 1, 2, ..., n
The mean x-coordinate (X) and mean y-coordinate (Y) can be calculated as:
- Mean X = (1/n) * Σxi = (1/n) * (np + (n(n-1)/2)a)
- Mean Y = (1/n) * Σyi = (1/n) * (nq + (n(n-1)/2)b)
Deriving the Equation
Now, we can simplify the expressions for mean X and mean Y to find a relationship between them. The mean coordinates can be rearranged as:
- Mean X = p + (n-1)/2 * a
- Mean Y = q + (n-1)/2 * b
To derive the equation, we eliminate the mean terms:
- Rearranging gives us the relationship: bx - ay = bp - aq.
This shows that the center of the mean position of the points lies on the line represented by the equation:
Final Answer
The correct answer is option 'C': bx - ay = bp - aq.
In the given problem, we have two sequences in Arithmetic Progression (A.P.):
- The first sequence: p, x1, x2, ..., xi, ..., q with a common difference of 'a'.
- The second sequence: y1, y2, ..., yi, ..., with a common difference of 'b'.
We need to find the mean position of the points Ai(xi, yi) and determine the equation of the line on which this mean position lies.
Mean Position of Points
The coordinates of the points Ai can be expressed as follows:
- The x-coordinates: xi = p + (i-1)a for i = 1, 2, ..., n
- The y-coordinates: yi = q + (i-1)b for i = 1, 2, ..., n
The mean x-coordinate (X) and mean y-coordinate (Y) can be calculated as:
- Mean X = (1/n) * Σxi = (1/n) * (np + (n(n-1)/2)a)
- Mean Y = (1/n) * Σyi = (1/n) * (nq + (n(n-1)/2)b)
Deriving the Equation
Now, we can simplify the expressions for mean X and mean Y to find a relationship between them. The mean coordinates can be rearranged as:
- Mean X = p + (n-1)/2 * a
- Mean Y = q + (n-1)/2 * b
To derive the equation, we eliminate the mean terms:
- Rearranging gives us the relationship: bx - ay = bp - aq.
This shows that the center of the mean position of the points lies on the line represented by the equation:
Final Answer
The correct answer is option 'C': bx - ay = bp - aq.
If α and β (α < β) be two different real roots of the equation ax2 + bx + c = 0, then- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
a)
b)
c)
d)
|
|
Mahi Reddy answered |
Also, f(x) is continuous and differentiable in [] as it is a polynomial function or x.
Hence, by Rolle's theorem, there exists a k in (), such that
If x = a cos3 θ, y = a sin3 θ, then
√[1 + (dy/dx)2] =- a)tan2 θ
- b)sec2 θ
- c)sec θ
- d)∣sec θ∣
Correct answer is option 'D'. Can you explain this answer?
If x = a cos3 θ, y = a sin3 θ, then
√[1 + (dy/dx)2] =
√[1 + (dy/dx)2] =
a)
tan2 θ
b)
sec2 θ
c)
sec θ
d)
∣sec θ∣
|
|
Simran Bajaj answered |
I cannot complete the question as it seems to be incomplete. Please provide more information.
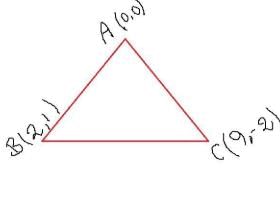
Points (0,0), (2,-1) and (9,2) are vertices of a triangle, then cosB =- a)(11/290)
- b)(√11/290)
- c)(-11/√290)
- d)-(√11/290)
Correct answer is option 'C'. Can you explain this answer?
Points (0,0), (2,-1) and (9,2) are vertices of a triangle, then cosB =
a)
(11/290)
b)
(√11/290)
c)
(-11/√290)
d)
-(√11/290)
|
Sameer Saha answered |
Given,
Vertices of a ΔABC are (0,0), (2,-1) and (9,2) are vertices of a triangle, then cosB =
From figure,
How many words are formed from the letters of the word EAMCET so that two vowels are never together?- a)360
- b)114
- c)72
- d)54
Correct answer is option 'C'. Can you explain this answer?
How many words are formed from the letters of the word EAMCET so that two vowels are never together?
a)
360
b)
114
c)
72
d)
54
|
|
Aditi Nambiar answered |
To solve this problem, we need to find the number of words that can be formed from the letters of the word "EAMCET" such that two vowels are never together.
First, let's determine the number of ways we can arrange the consonants. In the word "EAMCET", we have 3 consonants: M, C, and T. These can be arranged in 3! = 6 ways.
Next, let's consider the arrangement of the vowels A and E. Since we do not want two vowels to be together, we need to arrange them in such a way that there is at least one consonant between them.
To do this, we can treat the consonants M, C, and T as dividers. We can place the vowels in the spaces between these dividers.
There are 4 spaces between the consonants where the vowels can be placed: _M_C_T_.
To place the vowels, we need to choose 2 out of the 4 spaces. This can be done in C(4, 2) = 6 ways.
Now, let's consider the arrangement of the vowels themselves. Since we have 2 vowels (A and E), they can be arranged in 2! = 2 ways.
Therefore, the total number of words that can be formed from the letters of the word "EAMCET" such that two vowels are never together is 6 * 6 * 2 = 72.
Hence, the correct answer is option C) 72.
First, let's determine the number of ways we can arrange the consonants. In the word "EAMCET", we have 3 consonants: M, C, and T. These can be arranged in 3! = 6 ways.
Next, let's consider the arrangement of the vowels A and E. Since we do not want two vowels to be together, we need to arrange them in such a way that there is at least one consonant between them.
To do this, we can treat the consonants M, C, and T as dividers. We can place the vowels in the spaces between these dividers.
There are 4 spaces between the consonants where the vowels can be placed: _M_C_T_.
To place the vowels, we need to choose 2 out of the 4 spaces. This can be done in C(4, 2) = 6 ways.
Now, let's consider the arrangement of the vowels themselves. Since we have 2 vowels (A and E), they can be arranged in 2! = 2 ways.
Therefore, the total number of words that can be formed from the letters of the word "EAMCET" such that two vowels are never together is 6 * 6 * 2 = 72.
Hence, the correct answer is option C) 72.
In the expansion of (1 + x)n,coefficients of 2nd ,3rd and 4th terms are in A.P.Then n is equal to- a)7
- b)11
- c)9
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
a)
7
b)
11
c)
9
d)
none of these
|
|
Kritika Yadav answered |
Given Information:
- Coefficients of 2nd, 3rd, and 4th terms in the expansion of (1 + x)n are in A.P.
Solution:
Step 1: Finding the general term of the expansion
The general term in the expansion of (1 + x)n is given by:
T(r + 1) = nCr * (1)r * (x)n-r
Step 2: Finding the coefficients
Let's find the coefficients of the 2nd, 3rd, and 4th terms using the general term:
- Coefficient of the 2nd term (r = 1): nC1 = n
- Coefficient of the 3rd term (r = 2): nC2 = n(n-1)/2
- Coefficient of the 4th term (r = 3): nC3 = n(n-1)(n-2)/6
Step 3: Using the information given
Given that the coefficients of the 2nd, 3rd, and 4th terms are in A.P:
n, n(n-1)/2, n(n-1)(n-2)/6 are in A.P
Step 4: Solving the A.P
To find n, we can solve the A.P. using the formula for an A.P:
2 * (n(n-1)/2) = n + n(n-1)(n-2)/6
n(n-1) = 2n + n(n-1)(n-2)/3
3n(n-1) = 6n + n(n-1)(n-2)
3n^2 - 3n = 6n + n^3 - 3n^2 - n
n^3 - 6n^2 + 9n = 0
n(n - 3)^2 = 0
Therefore, n = 0 or n = 3. Since n cannot be 0, n = 3 is the solution.
Conclusion:
Therefore, the value of n is 3, which is not one of the options provided.
- Coefficients of 2nd, 3rd, and 4th terms in the expansion of (1 + x)n are in A.P.
Solution:
Step 1: Finding the general term of the expansion
The general term in the expansion of (1 + x)n is given by:
T(r + 1) = nCr * (1)r * (x)n-r
Step 2: Finding the coefficients
Let's find the coefficients of the 2nd, 3rd, and 4th terms using the general term:
- Coefficient of the 2nd term (r = 1): nC1 = n
- Coefficient of the 3rd term (r = 2): nC2 = n(n-1)/2
- Coefficient of the 4th term (r = 3): nC3 = n(n-1)(n-2)/6
Step 3: Using the information given
Given that the coefficients of the 2nd, 3rd, and 4th terms are in A.P:
n, n(n-1)/2, n(n-1)(n-2)/6 are in A.P
Step 4: Solving the A.P
To find n, we can solve the A.P. using the formula for an A.P:
2 * (n(n-1)/2) = n + n(n-1)(n-2)/6
n(n-1) = 2n + n(n-1)(n-2)/3
3n(n-1) = 6n + n(n-1)(n-2)
3n^2 - 3n = 6n + n^3 - 3n^2 - n
n^3 - 6n^2 + 9n = 0
n(n - 3)^2 = 0
Therefore, n = 0 or n = 3. Since n cannot be 0, n = 3 is the solution.
Conclusion:
Therefore, the value of n is 3, which is not one of the options provided.
If |z| = 4 and arg z = (5π/6), then the value of z is- a)2√3 - 2i
- b)2√3 + 2i
- c)-2√3 + 2i
- d)-√3 + i
Correct answer is option 'C'. Can you explain this answer?
a)
2√3 - 2i
b)
2√3 + 2i
c)
-2√3 + 2i
d)
-√3 + i
|
|
Tushar Jain answered |
Solution:
Given, |z| = 4 and arg z = (5π/6)
We know that, z = |z| (cos θ + i sin θ)
where, cos θ = Re(z) / |z| and sin θ = Im(z) / |z|
Putting the given values, we get
z = 4 (cos (5π/6) + i sin (5π/6))
z = 4 (-√3/2 + i/2)
z = -2√3 + 2i
Therefore, the correct answer is option 'C' (-2√3 2i).
Given, |z| = 4 and arg z = (5π/6)
We know that, z = |z| (cos θ + i sin θ)
where, cos θ = Re(z) / |z| and sin θ = Im(z) / |z|
Putting the given values, we get
z = 4 (cos (5π/6) + i sin (5π/6))
z = 4 (-√3/2 + i/2)
z = -2√3 + 2i
Therefore, the correct answer is option 'C' (-2√3 2i).
The solution of the equation (1+x2)(1+y)dy+(1+x)(1+y2)dx=0 is- a)tan⁻1x+log(1+x2)+tan⁻1y+log(1+y2)=c
- b)tan⁻1x-(1/2)log(1+x2)+tan⁻1y-(1/2)log(1+y2)=c
- c)tan⁻1x+(1/2)log(1+x2)+tan⁻1y+(1/2)log(1+y2)=c
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The solution of the equation (1+x2)(1+y)dy+(1+x)(1+y2)dx=0 is
a)
tan⁻1x+log(1+x2)+tan⁻1y+log(1+y2)=c
b)
tan⁻1x-(1/2)log(1+x2)+tan⁻1y-(1/2)log(1+y2)=c
c)
tan⁻1x+(1/2)log(1+x2)+tan⁻1y+(1/2)log(1+y2)=c
d)
none of these
|
|
Rahul Bansal answered |
The given differential equation is nonlinear, so it cannot be solved using standard techniques like separation of variables. To solve this equation, we can try to rearrange it into a standard form that can be recognized as a known differential equation.
We can rewrite the given equation as:
(1+y)(1+y^2)dy + (1+x)(1+x^2)dx = 0
This equation can be rearranged as follows:
(1+y^2)dy + (1+x^2)dx = -(1+y)(1+x)
This equation can be rewritten as:
dy/dx = (1+x)/(1+y) - (1+y^2)/(1+x^2)
This equation is in the form dy/dx = f(x,y), which is the standard form of a first-order differential equation. This equation can be recognized as a separable differential equation, which means that it can be solved using separation of variables.
To solve this equation using separation of variables, we can isolate the dy term on one side of the equation and the dx term on the other side, and then integrate both sides. This gives:
∫(1+y^2)dy = -∫(1+x)(1+x^2)dx
Solving for y, we get:
tan⁻1y + (1/2)log(1+y^2) = -∫(1+x)(1+x^2)dx + C
Where C is an integration constant.
Similarly, we can solve for x to get:
tan⁻1x + (1/2)log(1+x^2) = -∫(1+y)(1+y^2)dy + D
Where D is an integration constant.
Therefore, the solution of the differential equation is:
tan⁻1x + (1/2)log(1+x^2) + tan⁻1y + (1/2)log(1+y^2) = C + D
This is equivalent to:
c) tan⁻1x+(1/2)log(1+x^2)+tan⁻1y+(1/2)log(1+y^2)=c
Given that f(x) is continuously differentiable on a ≤ x ≤ b where a < b , f a < 0 and f b > 0, which of the following are always true ?
(i) f(x) is bounded on a ≤ x ≤ b .
(ii) The equation f(x) = 0 has at least one solution in a < x < b .
(iii) The maximum and minimum values of f(x) on a ≤ x ≤ b occur at points where f ′ c = 0
(iv) There is at least one point c with a < c < b where f ′ c > 0.
(v) There is at least one point d with a < d < b where f ′ c < 0.- a)Only (ii) and (iv) are true
- b)All but (iii) are true
- c)All but (v) are true
- d)Only (i), (ii) and (iv) are true
Correct answer is option 'D'. Can you explain this answer?
Given that f(x) is continuously differentiable on a ≤ x ≤ b where a < b , f a < 0 and f b > 0, which of the following are always true ?
(i) f(x) is bounded on a ≤ x ≤ b .
(ii) The equation f(x) = 0 has at least one solution in a < x < b .
(iii) The maximum and minimum values of f(x) on a ≤ x ≤ b occur at points where f ′ c = 0
(iv) There is at least one point c with a < c < b where f ′ c > 0.
(v) There is at least one point d with a < d < b where f ′ c < 0.
(i) f(x) is bounded on a ≤ x ≤ b .
(ii) The equation f(x) = 0 has at least one solution in a < x < b .
(iii) The maximum and minimum values of f(x) on a ≤ x ≤ b occur at points where f ′ c = 0
(iv) There is at least one point c with a < c < b where f ′ c > 0.
(v) There is at least one point d with a < d < b where f ′ c < 0.
a)
Only (ii) and (iv) are true
b)
All but (iii) are true
c)
All but (v) are true
d)
Only (i), (ii) and (iv) are true
|
|
Saumya Choudhury answered |
(i) This statement is true, every continuous function is bounded on a closed interval.
(ii) True again, by Intermediate Value Theorem.
(iii) Not ture, because maximum and/or minimum value could also occur at a or b, without the derivatives being O.
(iv) True By the Mean Value Theorem, there exists a point betweem a and b, where the derivative is exactly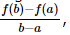
a clearly positive value.
(v) Not always true, for example, the function might be strictly increasing guaranteeing the derivative to be always positive.
Thus, the true statements are (i), (ii) and (iv).
(ii) True again, by Intermediate Value Theorem.
(iii) Not ture, because maximum and/or minimum value could also occur at a or b, without the derivatives being O.
(iv) True By the Mean Value Theorem, there exists a point betweem a and b, where the derivative is exactly
a clearly positive value.(v) Not always true, for example, the function might be strictly increasing guaranteeing the derivative to be always positive.
Thus, the true statements are (i), (ii) and (iv).
If y=sin((1+x2)/(1-x2)), (dy/dx)=- a)[(4x)/(1-x2)]. cos[(1+x2)/(1-x2)]
- b)[(x)/(1-x2)2]. cos[(1+x2)/(1-x2)]
- c)[(x)/(1-x2)]. cos[(1+x2)/(1-x2)]
- d)4x × cos((1 + x²) / (1 − x²)) / (1 − x²)²
Correct answer is option 'D'. Can you explain this answer?
If y=sin((1+x2)/(1-x2)), (dy/dx)=
a)
[(4x)/(1-x2)]. cos[(1+x2)/(1-x2)]
b)
[(x)/(1-x2)2]. cos[(1+x2)/(1-x2)]
c)
[(x)/(1-x2)]. cos[(1+x2)/(1-x2)]
d)
4x × cos((1 + x²) / (1 − x²)) / (1 − x²)²
|
Learners Habitat answered |
Given:
y = sin((1 + x²) / (1 − x²))
y = sin((1 + x²) / (1 − x²))
We are to find dy/dx.
Step 1: Identify inner and outer functions
Let:
u = (1 + x²) / (1 − x²) ← inner function
y = sin(u) ← outer function
u = (1 + x²) / (1 − x²) ← inner function
y = sin(u) ← outer function
Step 2: Differentiate using chain rule
Using the chain rule:
dy/dx = dy/du × du/dx
dy/dx = dy/du × du/dx
We know:
dy/du = cos(u)
dy/du = cos(u)
Step 3: Differentiate u
To find du/dx for u = (1 + x²) / (1 − x²), use the quotient rule:
du/dx = [(1 − x²)(d/dx(1 + x²)) − (1 + x²)(d/dx(1 − x²))] / (1 − x²)²
Now compute derivatives:
d/dx(1 + x²) = 2x
d/dx(1 − x²) = −2x
d/dx(1 + x²) = 2x
d/dx(1 − x²) = −2x
So:
du/dx = [(1 − x²)(2x) − (1 + x²)(−2x)] / (1 − x²)²
du/dx = [(1 − x²)(2x) − (1 + x²)(−2x)] / (1 − x²)²
Simplify numerator:
= (1 − x²)(2x) + (1 + x²)(2x)
= 2x(1 − x² + 1 + x²)
= 2x(2)
= 4x
= (1 − x²)(2x) + (1 + x²)(2x)
= 2x(1 − x² + 1 + x²)
= 2x(2)
= 4x
So:
du/dx = 4x / (1 − x²)²
du/dx = 4x / (1 − x²)²
Step 4: Combine the results
dy/dx = cos((1 + x²) / (1 − x²)) × 4x / (1 − x²)²
Final Answer:
dy/dx = 4x × cos((1 + x²) / (1 − x²)) / (1 − x²)²
dy/dx = 4x × cos((1 + x²) / (1 − x²)) / (1 − x²)²
P,Q,R and S have to deliver lecture, then in how many ways can the lectures be arranged?- a) 4
- b) 12
- c) 256
- d) 24
Correct answer is option 'D'. Can you explain this answer?
a)
4
b)
12
c)
256
d)
24
|
Jaya Das answered |
Problem: We have to arrange the lectures of P, Q, R and S. In how many ways can we do that?
Solution:
There are 4 lectures that we have to arrange. We can arrange them in the following ways:
1. P first, then Q, then R, then S
2. P first, then Q, then S, then R
3. P first, then R, then Q, then S
4. P first, then R, then S, then Q
5. P first, then S, then Q, then R
6. P first, then S, then R, then Q
7. Q first, then P, then R, then S
8. Q first, then P, then S, then R
9. Q first, then R, then P, then S
10. Q first, then R, then S, then P
11. Q first, then S, then P, then R
12. Q first, then S, then R, then P
13. R first, then P, then Q, then S
14. R first, then P, then S, then Q
15. R first, then Q, then P, then S
16. R first, then Q, then S, then P
17. R first, then S, then P, then Q
18. R first, then S, then Q, then P
19. S first, then P, then Q, then R
20. S first, then P, then R, then Q
21. S first, then Q, then P, then R
22. S first, then Q, then R, then P
23. S first, then R, then P, then Q
24. S first, then R, then Q, then P
Therefore, there are 24 ways to arrange the lectures of P, Q, R and S.
Hence, the correct option is D.
Solution:
There are 4 lectures that we have to arrange. We can arrange them in the following ways:
1. P first, then Q, then R, then S
2. P first, then Q, then S, then R
3. P first, then R, then Q, then S
4. P first, then R, then S, then Q
5. P first, then S, then Q, then R
6. P first, then S, then R, then Q
7. Q first, then P, then R, then S
8. Q first, then P, then S, then R
9. Q first, then R, then P, then S
10. Q first, then R, then S, then P
11. Q first, then S, then P, then R
12. Q first, then S, then R, then P
13. R first, then P, then Q, then S
14. R first, then P, then S, then Q
15. R first, then Q, then P, then S
16. R first, then Q, then S, then P
17. R first, then S, then P, then Q
18. R first, then S, then Q, then P
19. S first, then P, then Q, then R
20. S first, then P, then R, then Q
21. S first, then Q, then P, then R
22. S first, then Q, then R, then P
23. S first, then R, then P, then Q
24. S first, then R, then Q, then P
Therefore, there are 24 ways to arrange the lectures of P, Q, R and S.
Hence, the correct option is D.
Chapter doubts & questions for Mathematics - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mathematics - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026
3 videos|21 docs|54 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup