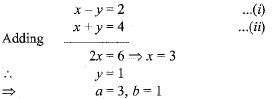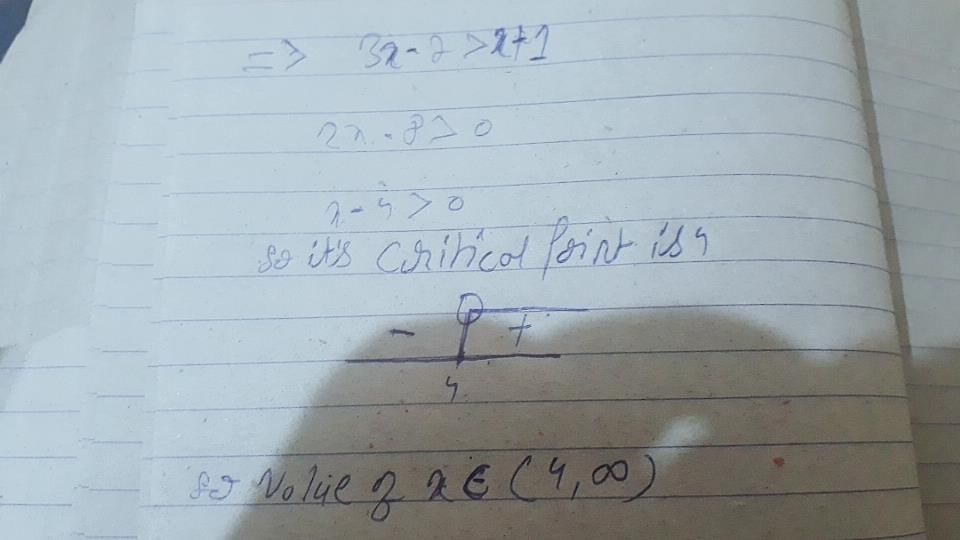All Exams >
Class 10 >
Mathematics Class 10 (Maharashtra SSC Board) >
All Questions
All questions of Linear Equations in Two Variables for Class 10 Exam
A pair of linear equations which has a unique solution x = 2, y = - 3 is
- a)x + y = -1; 2x - 3y = -5
- b)x - 4y - 14 = 0; 5x - y - 13 = 0
- c)2x - y = 1 ; 3x + 2y = 0
- d)2x + 5y = -11; 4x + 10y = -23
Correct answer is option 'B'. Can you explain this answer?
A pair of linear equations which has a unique solution x = 2, y = - 3 is
a)
x + y = -1; 2x - 3y = -5
b)
x - 4y - 14 = 0; 5x - y - 13 = 0
c)
2x - y = 1 ; 3x + 2y = 0
d)
2x + 5y = -11; 4x + 10y = -23
|
|
Vikram Kapoor answered |
x - 4y -14 = 0
x = 4y+14
putting this in 5x - y -13 = 0
5(4y+14) - y -13 =0
19y = -57
y = -3
putting y = -3 in x = 4y+14
x = 4(-3)+14
x = 2
so option b is correct
If am ≠ bl, then the system of equations, ax + by = c, lx + my = n- a)has a unique solution
- b)has no solution
- c)has infinitely many solutions
- d)may or may not have a solution
Correct answer is option 'A'. Can you explain this answer?
If am ≠ bl, then the system of equations, ax + by = c, lx + my = n
a)
has a unique solution
b)
has no solution
c)
has infinitely many solutions
d)
may or may not have a solution
|
|
Vivek Rana answered |
If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.
Given,
Pair of lines represented by the equations
ax + by = c
lx + my = n
For unique solution

For infinite solutions
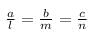
For no solution

Given,
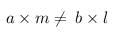
This can be transformed into
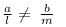
Therefore, If am ≠ bl, then the equations ax+by=c, lx+my=n has a unique solution.
The sum of the digits of a two-digit number is 9. If 27 is added to it, the digit of number get reversed. The number is- a)25
- b)72
- c)63
- d)36
Correct answer is option 'D'. Can you explain this answer?
The sum of the digits of a two-digit number is 9. If 27 is added to it, the digit of number get reversed. The number is
a)
25
b)
72
c)
63
d)
36
|
|
Avinash Patel answered |
Lets,
First digit number = x
Second digit number = y
Number = (x+10y)
A/Q,
x + y = 9 ...................... (i)
A/Q,
(x+10y) = (10x+y) + 27
x + 10y = 10x + y +27
9x - 9y = 27
9(x - y) = 27
x - y = 27/9
x - y = 3 ......................... (ii)
Equation (i) and (ii) we get,
x = 3
Putting the value of x in eq.(i)
we get,
y = 6
Number = (10x +y)
= 10 x 3 + 6
= 30 + 6
= 36
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:- a)One solution
- b)Infinitely many solutions
- c)No solutions
- d)Two solutions
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:
a)
One solution
b)
Infinitely many solutions
c)
No solutions
d)
Two solutions
|
|
Gaurav Kumar answered |
We have a1, a2 the coefficients of x2,b1 and b2 coefficients of x and c1 and c2 the constant terms. So,
So,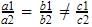 a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
 So,
So,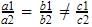 a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.The pair of equations y = 0 and y = - 7 has- a)one solution
- b)two solutions
- c)infinitely many solutions
- d)no solution
Correct answer is option 'D'. Can you explain this answer?
The pair of equations y = 0 and y = - 7 has
a)
one solution
b)
two solutions
c)
infinitely many solutions
d)
no solution
|
|
Gaurav Kumar answered |
The equation are y=0 and y=-7
y=0 is on the x-axis and y=-7 is the line parallel to the x-axes at a distance 7 units from y=0
The line will be parallel
if we try to solve these equations we get 0=7 which is absurd.
So the equations are inconsistent.
Therefore there is no solution.
y=0 is on the x-axis and y=-7 is the line parallel to the x-axes at a distance 7 units from y=0
The line will be parallel
if we try to solve these equations we get 0=7 which is absurd.
So the equations are inconsistent.
Therefore there is no solution.
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –- a)k = 2
- b)k = 6
- c)k = 6
- d)k = 3
Correct answer is option 'A'. Can you explain this answer?
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –
a)
k = 2
b)
k = 6
c)
k = 6
d)
k = 3
|
|
Naina Sharma answered |
An equation has infinitely many solutions when the lines are coincident.
The lines are coincident when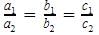
So 3x + 4y = k, 9x + 12y = 6 are coincident when
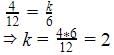
The lines are coincident when
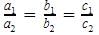
So 3x + 4y = k, 9x + 12y = 6 are coincident when
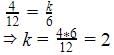
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?- a)x = 5, y = 3
- b)x = 2, y = 1
- c)x = 6, y = 7
- d)x = 4, y = 4
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?
a)
x = 5, y = 3
b)
x = 2, y = 1
c)
x = 6, y = 7
d)
x = 4, y = 4
|
|
Vikram Kapoor answered |
3x – 2y = 4 and 6x – 4y = 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. The present age of the man is –- a)28 years
- b)30 years
- c)32 years
- d)34 years
Correct answer is option 'B'. Can you explain this answer?
Six years hence a man's age will be three times the age of his son and three years ago he was nine times as old as his son. The present age of the man is –
a)
28 years
b)
30 years
c)
32 years
d)
34 years

|
Dr Manju Sen answered |
Let the present age of man is x and of son is y.
Six years hence,
Man’s age =x+6
Son’s age=y+6
Man’s age is 3 times son’s age
x+6=3(y+6)
x+6=3y+18
x=3y+12 …...1
Three years ago,
Man’s age =x-3
Son’s age=y-3
Man’s age was 9 times as of son
x-3=9(y-3)
x-3=9y-27
x=9y-24 ….2
From 1 and 2
3y+12=9y-24
6y=36
y=6
x=3*6+12=18+12=30 years
Six years hence,
Man’s age =x+6
Son’s age=y+6
Man’s age is 3 times son’s age
x+6=3(y+6)
x+6=3y+18
x=3y+12 …...1
Three years ago,
Man’s age =x-3
Son’s age=y-3
Man’s age was 9 times as of son
x-3=9(y-3)
x-3=9y-27
x=9y-24 ….2
From 1 and 2
3y+12=9y-24
6y=36
y=6
x=3*6+12=18+12=30 years
One equation of a pair of dependent linear equations is -5x + 7y = 2, the second equation can be :- a)-10x + 14y + 4 = 0
- b)-10x – 14x + 4 =
- c)10x – 14y = -4
- d)10x + 14y + 4 =0
Correct answer is option 'C'. Can you explain this answer?
One equation of a pair of dependent linear equations is -5x + 7y = 2, the second equation can be :
a)
-10x + 14y + 4 = 0
b)
-10x – 14x + 4 =
c)
10x – 14y = -4
d)
10x + 14y + 4 =0
|
|
Vikram Kapoor answered |
If a system of two linear equation is consistent system and has an infinite number of solutions, it is dependent . When you graph the equations, both equations represent the same line.So we have  which is satisfied by 10x – 14y = -4 only.
which is satisfied by 10x – 14y = -4 only.
 which is satisfied by 10x – 14y = -4 only.
which is satisfied by 10x – 14y = -4 only.The pair of linear equations 2x + 3y = 5 and 4x + 6y = 10 is- a)inconsistent
- b)Both
- c)consistent
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations 2x + 3y = 5 and 4x + 6y = 10 is
a)
inconsistent
b)
Both
c)
consistent
d)
none of these
|
|
Amit Sharma answered |
a1 / a2 = b1 / b2 = c1 / c2
2/4 = 3/6 = 5/10
1/2 = 1/2 = 1/2
So, a1 / a2 = b1 / b2 = c1 / c2
When these are equal then it is consistent.
Therefore option (C) is correct .
2/4 = 3/6 = 5/10
1/2 = 1/2 = 1/2
So, a1 / a2 = b1 / b2 = c1 / c2
When these are equal then it is consistent.
Therefore option (C) is correct .
If a pair of linear equations has infinitely many solutions, then the lines representing them will be
- a)Parallel
- b)Intersecting lines
- c)Always intersecting
- d)coincident lines
Correct answer is option 'D'. Can you explain this answer?
If a pair of linear equations has infinitely many solutions, then the lines representing them will be
a)
Parallel
b)
Intersecting lines
c)
Always intersecting
d)
coincident lines
|
|
Ananya Das answered |
If two lines i.e. a pair of linear equations, has infinitely many solutions it means lines are overlapping each other i.e. coincident lines.


The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son. The present ages (in years) of the son and the father are, respectively. - a)4 and 24
- b)5 and 30
- c)6 and 36
- d)3 and 24
Correct answer is option 'C'. Can you explain this answer?
The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son. The present ages (in years) of the son and the father are, respectively.
a)
4 and 24
b)
5 and 30
c)
6 and 36
d)
3 and 24
|
|
Ååryañ answered |

The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if –
- a)k ≠ -3
- b)k = 3
- c)k = 5
- d)k = -5
Correct answer is option 'A'. Can you explain this answer?
The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if –
a)
k ≠ -3
b)
k = 3
c)
k = 5
d)
k = -5
|
|
Rohit Sharma answered |
Given :
2 k x + 5 y – 7 = 0 ...( i )
6 x – 5 y – 1 = 0 ... ( ii )
Pair of linear equations has a unique solution.
We know for unique solution.
6 x – 5 y – 1 = 0 ... ( ii )
Pair of linear equations has a unique solution.
We know for unique solution.
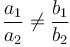
Comparing from ( i ) and ( ii ) we have

Put these values in formula.
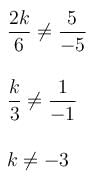
Thus we get answer many values of k but leaving k ≠ -3.
The pair of linear equations 2x + 5y = k, kx + 15y = 18 has infinitely many solutions if –- a)k = 3
- b)k = 6
- c)k = 9
- d)k = 18
Correct answer is option 'B'. Can you explain this answer?
The pair of linear equations 2x + 5y = k, kx + 15y = 18 has infinitely many solutions if –
a)
k = 3
b)
k = 6
c)
k = 9
d)
k = 18
|
|
Vivek Rana answered |
An equation has infinitely many solutions when the lines are coincident.
The lines are coincident when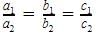
So 2x + 5y = k, kx + 15y = 18 are coincident when

The lines are coincident when
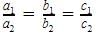
So 2x + 5y = k, kx + 15y = 18 are coincident when

For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution- a)3
- b)2
- c)1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution
a)
3
b)
2
c)
1
d)
-2
|
|
Krishna Iyer answered |
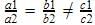 is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent
is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1
b1=1,b2=k-1,c1=-1,c2=-2k-1
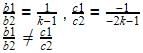
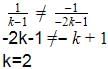
Can you explain the answer of this question below:The pair of equations y = 0 and y = -7 has :
- A:
no solution
- B:
infinitely many solutions
- C:
one solution
- D:
two solutions
The answer is a.
The pair of equations y = 0 and y = -7 has :
no solution
infinitely many solutions
one solution
two solutions
|
|
Raghav Bansal answered |
y=0 is x-axis… since every point has y=0. y=-7 is a line parallel to x-axis passing through x=0,y=-7. So the two lines are parallel to each other and are inconsistent which means that it has no solutions because it will never meet.
Which of following is not a solution of 3a + b = 12 ?
- a)(3, 3)
- b)(5, -3)
- c)(4, 0)
- d)(2, 4)
Correct answer is option 'D'. Can you explain this answer?
Which of following is not a solution of 3a + b = 12 ?
a)
(3, 3)
b)
(5, -3)
c)
(4, 0)
d)
(2, 4)

|
Prashant Gujjar Pgv answered |
D correct h 3(2)+4=10this is not a solution
Which of the following pair of linear equations is inconsistent?- a)5x – 3y = 11; 7x + 2y =13
- b)x – 2y = 6; 2x + 3y = 4
- c)9x – 8y = 17; 18x -16y = 34
- d)2x + 3y = 7; 4x + 6y = 5
Correct answer is option 'D'. Can you explain this answer?
Which of the following pair of linear equations is inconsistent?
a)
5x – 3y = 11; 7x + 2y =13
b)
x – 2y = 6; 2x + 3y = 4
c)
9x – 8y = 17; 18x -16y = 34
d)
2x + 3y = 7; 4x + 6y = 5
|
|
Krishna Iyer answered |
Pair of linear equations are inconsistent when they are parallel. When the two equations are parallel ,we have  .
.
 .
.In D, we have 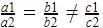 which is
which is 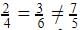 , so it is inconsistent.
, so it is inconsistent.
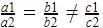 which is
which is 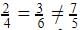 , so it is inconsistent.
, so it is inconsistent.The pair of linear equations kx + 4y = 5, 3x + 2y = 5 is consistent only when –- a)k≌6
- b)k = 6
- c)k≌3
- d)k = 3
Correct answer is option 'A'. Can you explain this answer?
The pair of linear equations kx + 4y = 5, 3x + 2y = 5 is consistent only when –
a)
k≌6
b)
k = 6
c)
k≌3
d)
k = 3
|
|
Aditya Shah answered |
kx + 4y = 5, 3x + 2y = 5
Here, a1=k,b1=4,c1=−5
and a2=3,b2=2,c2=-5
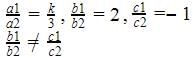
So , The equation is consistent when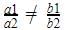
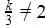
k ≠ 6
Here, a1=k,b1=4,c1=−5
and a2=3,b2=2,c2=-5
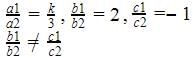
So , The equation is consistent when
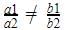
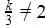
k ≠ 6
The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:- a)None
- b)Infinitely many
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:
a)
None
b)
Infinitely many
c)
0
d)
1
|
|
Pooja Shah answered |
We have the equations x + 2y – 8 = 0 and 2x + 4y = 16 Where 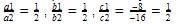
Here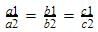 which is the case of coincident lines . So there are infinitely many solutions.
which is the case of coincident lines . So there are infinitely many solutions.
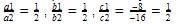
Here
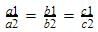 which is the case of coincident lines . So there are infinitely many solutions.
which is the case of coincident lines . So there are infinitely many solutions.A system of simultaneous linear equations has infinitely many solutions if two lines:- a)are coincident
- b)intersect at two points
- c)are parallel
- d)intersect at one point
Correct answer is option 'A'. Can you explain this answer?
A system of simultaneous linear equations has infinitely many solutions if two lines:
a)
are coincident
b)
intersect at two points
c)
are parallel
d)
intersect at one point
|
|
Damini kumar answered |
Explanation:
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Which of the following pairs of equations represent inconsistent system?- a)3x – y = -8 3x – y = 24
- b)5x – y = 10 10x – 2y = 20
- c)3x – 2y = 8 2x + 3y = 1
- d)lx – y = m x + my = l
Correct answer is option 'A'. Can you explain this answer?
Which of the following pairs of equations represent inconsistent system?
a)
3x – y = -8 3x – y = 24
b)
5x – y = 10 10x – 2y = 20
c)
3x – 2y = 8 2x + 3y = 1
d)
lx – y = m x + my = l
|
|
Amit Sharma answered |
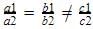 is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent.
is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent.3x – y = -8 ,3x – y = 24
3x – y +8=0 ,3x – y -24=0
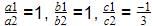
So,
 Therefore the equations are inconsistent.
Therefore the equations are inconsistent.The pair of equations x = a and y = b graphically represents lines which are- a)parallel
- b)intersecting at (b, a)
- c)coincident
- d)intersecting at (a, b)
Correct answer is option 'D'. Can you explain this answer?
The pair of equations x = a and y = b graphically represents lines which are
a)
parallel
b)
intersecting at (b, a)
c)
coincident
d)
intersecting at (a, b)
|
|
Raghav Bansal answered |
By graphically in every condition, if a, b>>0; a, b< 0, a>0, b< 0; a<0, b>0 but a = b≠ 0.
The pair of equations x = a and y = b graphically represents lines which are intersecting at (a, b).
If a, b > 0
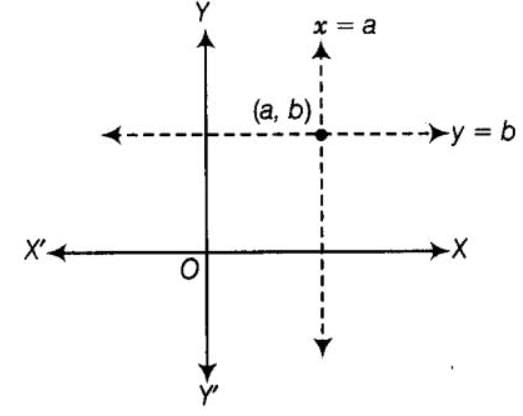
Similarly, in all cases two lines intersect at (a, b).
The pair of equations x = a and y = b graphically represents lines which are intersecting at (a, b).
If a, b > 0

Similarly, in all cases two lines intersect at (a, b).
The pair of linear equations 8x – 5y = 7 and 5x – 8y = -7 have :- a)No solution
- b)Many solutions
- c)One solution
- d)Two solutions
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations 8x – 5y = 7 and 5x – 8y = -7 have :
a)
No solution
b)
Many solutions
c)
One solution
d)
Two solutions
|
|
Raghav Bansal answered |
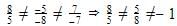 So, they are intersecting lines. And intersecting lines meet at only one point. So only 1 solution is available.
So, they are intersecting lines. And intersecting lines meet at only one point. So only 1 solution is available.Which of the following equation is not a linear equation?- a)2a-b =1
- b)2a+b =1
- c)a+b =1
- d)√a+b =1
Correct answer is option 'D'. Can you explain this answer?
Which of the following equation is not a linear equation?
a)
2a-b =1
b)
2a+b =1
c)
a+b =1
d)
√a+b =1
|
|
Gaurav Kumar answered |
Linear equation is an equation between two variables that gives a straight line when plotted on a graph. Linear equations have degree 1 only which means that power of the variables is 1 only. Since 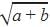 does not have degree 1 its not a linear equation.
does not have degree 1 its not a linear equation.
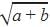 does not have degree 1 its not a linear equation.
does not have degree 1 its not a linear equation.The pair of linear equations 3x + 7y = k, 12x + 2ky = 4k + 1 do not have any solution if
- a)k = 7
- b)k = 14
- c)k = 21
- d)k = 28
Correct answer is option 'B'. Can you explain this answer?
The pair of linear equations 3x + 7y = k, 12x + 2ky = 4k + 1 do not have any solution if
a)
k = 7
b)
k = 14
c)
k = 21
d)
k = 28
|
|
Anirudh Mukherjee answered |
Explanation:
Given pair of linear equations are:
3x - 7y = k ...(1)
12x - 2ky = 4k - 1 ...(2)
We need to find the value of k for which these equations do not have any solution.
Method:
If a pair of linear equations do not have any solution, it means they are inconsistent. Two linear equations are inconsistent if their slopes are equal but their y-intercepts are not equal.
We can rearrange the given equations into slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
Equation (1) can be rearranged as:
y = (3/7)x - (k/7) ...(3)
Equation (2) can be rearranged as:
y = (6/k)x - (2k-1)/(2k) ...(4)
Comparing equations (3) and (4), we get:
m1 = 3/7 and m2 = 6/k
For the pair of equations to be inconsistent, m1 = m2 and b1 ≠ b2.
Equating the slopes, we get:
3/7 = 6/k
Solving for k, we get:
k = 14
Now, substituting k = 14 in equations (1) and (2), we get:
3x - 7y = 14 ...(5)
12x - 28y = 55 ...(6)
Multiplying equation (5) by 4, we get:
12x - 28y = 56 ...(7)
Comparing equations (6) and (7), we see that the y-intercepts are not equal. Hence, the given pair of equations are consistent for k = 14.
Conclusion:
Thus, the given pair of linear equations 3x - 7y = k, 12x - 2ky = 4k - 1 do not have any solution if k = 14. Therefore, the correct option is (B).
Given pair of linear equations are:
3x - 7y = k ...(1)
12x - 2ky = 4k - 1 ...(2)
We need to find the value of k for which these equations do not have any solution.
Method:
If a pair of linear equations do not have any solution, it means they are inconsistent. Two linear equations are inconsistent if their slopes are equal but their y-intercepts are not equal.
We can rearrange the given equations into slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
Equation (1) can be rearranged as:
y = (3/7)x - (k/7) ...(3)
Equation (2) can be rearranged as:
y = (6/k)x - (2k-1)/(2k) ...(4)
Comparing equations (3) and (4), we get:
m1 = 3/7 and m2 = 6/k
For the pair of equations to be inconsistent, m1 = m2 and b1 ≠ b2.
Equating the slopes, we get:
3/7 = 6/k
Solving for k, we get:
k = 14
Now, substituting k = 14 in equations (1) and (2), we get:
3x - 7y = 14 ...(5)
12x - 28y = 55 ...(6)
Multiplying equation (5) by 4, we get:
12x - 28y = 56 ...(7)
Comparing equations (6) and (7), we see that the y-intercepts are not equal. Hence, the given pair of equations are consistent for k = 14.
Conclusion:
Thus, the given pair of linear equations 3x - 7y = k, 12x - 2ky = 4k - 1 do not have any solution if k = 14. Therefore, the correct option is (B).
The pairs of equations 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0 have- a)Unique solution
- b)Exactly two solutions
- c)No solution
- d)Infinitely many solutions
Correct answer is option 'C'. Can you explain this answer?
The pairs of equations 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0 have
a)
Unique solution
b)
Exactly two solutions
c)
No solution
d)
Infinitely many solutions
|
|
Meera Rana answered |
Given, 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2
c1/c2 = 12/26 = 6/13
Since, a1/a2 = b1/b2 ≠ c1/c2
So, the pairs of equations are parallel and the lines never intersect each other at any point, therefore there is no possible solution.
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2
c1/c2 = 12/26 = 6/13
Since, a1/a2 = b1/b2 ≠ c1/c2
So, the pairs of equations are parallel and the lines never intersect each other at any point, therefore there is no possible solution.
8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
- a)120, 130
- b)140,280
- c)240,280
- d)100,120
Correct answer is option 'B'. Can you explain this answer?
8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
a)
120, 130
b)
140,280
c)
240,280
d)
100,120
|
|
Vikas Kumar answered |
Work done by 1 girl and 1 boy in x and y days respectively.
work done by 1 girl and 1 boy in 1 day is (1/x) and (1/y).
so, work done by 8 girls and 12 boys in 1 day is (8/x) + (12/y) = 1/10
let (1/x) = a and (1/y) = b
so, 8a + 12b = 1/10
→ 80a + 120b = 1 ---- (1)
work done by 6 girls and 8 boys in 1 day is (6/x) + (8/y) = 1/14
6a + 80 = 1/14
→ 84a + 112b = 1 ---- (2)
By elimination method, Multiple equation 1 by 21 on both sides, we get
1680a + 2520b = 21 ---- (3)
Multiply equation 2 by 20 on both sides, we get
1680a + 2240b = 20 ---- (4)
On solving equation 3 and 4, we get
2520 b - 2240b = 21 - 20
→ 280 b = 1
→ b = 1/280
b =1/y
→ 1/280 = 1/y
→ y = 280
80a + 120 x (1/280) = 1 (From 1)
→ 80a + (3/7) = 1
→ 80a = 1 - (3/7)
→ 80a = (7 - 3)/7
→ 80a = 4/7
→ a = 4/(7 × 80)
→ a = 1/140
→ a = 1/x
→ 1/140 = 1/x
→ x = 140
1 girl and 1 boy alone take 140 days and 280 days to complete a work.
If the pair of equation has no solution, then the pair of equation is :- a)inconsistent
- b)coincident
- c)consistent
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If the pair of equation has no solution, then the pair of equation is :
a)
inconsistent
b)
coincident
c)
consistent
d)
none of these
|
|
Vikas Kumar answered |
If two lines are parallel then, they have no solution pair of linear equations is inconsistent;
If two lines are coincident then, they have infinite solution and pair of linear equations is consistent;
If two lines are intersecting then, they have unique solution and pair of linear equations is consistent.
If one equation of a pair of dependent linear equations is -3x + 5y - 2 = 0. The second equation will be:- a)6x - 10y - 4 = 0
- b)-6x + 10y - 4 = 0
- c)6x + 10y - 4 = 0
- d)-6x + 10y + 4 = 0
Correct answer is option 'B'. Can you explain this answer?
If one equation of a pair of dependent linear equations is -3x + 5y - 2 = 0. The second equation will be:
a)
6x - 10y - 4 = 0
b)
-6x + 10y - 4 = 0
c)
6x + 10y - 4 = 0
d)
-6x + 10y + 4 = 0
|
|
Avinash Patel answered |
The condition for dependent linear equations is:
a1/a2 = b1/b2 = c1/c2
For option a,
a1/a2 = b1/b2 ≠ c1/c2 = ½
a1/a2 = b1/b2 = c1/c2
For option a,
a1/a2 = b1/b2 ≠ c1/c2 = ½
If the lines 3x + 2ky – 2 = 0 and 2x + 5y + 1 = 0 are parallel, then what is the value of k?- a)4/15
- b)4/5
- c)5/4
- d)15/4
Correct answer is option 'D'. Can you explain this answer?
If the lines 3x + 2ky – 2 = 0 and 2x + 5y + 1 = 0 are parallel, then what is the value of k?
a)
4/15
b)
4/5
c)
5/4
d)
15/4
|
|
Kavya nambiar answered |
I'm sorry, it seems like the question is incomplete. Can you please provide the full question?
Three chairs and two tables cost Rs. 1850. Five chairs and three tables cost Rs. 2850. Then the total cost of one chair and one table is –- a)Rs. 800
- b)Rs. 850
- c)Rs. 900
- d)Rs. 950
Correct answer is option 'B'. Can you explain this answer?
Three chairs and two tables cost Rs. 1850. Five chairs and three tables cost Rs. 2850. Then the total cost of one chair and one table is –
a)
Rs. 800
b)
Rs. 850
c)
Rs. 900
d)
Rs. 950
|
|
Niyati nayar answered |
Understanding the Problem
We have two equations based on the information provided about chairs and tables:
1. Equation from the first statement:
- 3 chairs + 2 tables = Rs. 1850
- Let the cost of one chair be C and one table be T.
- This gives us the equation: 3C + 2T = 1850
2. Equation from the second statement:
- 5 chairs + 3 tables = Rs. 2850
- This gives us the equation: 5C + 3T = 2850
Solving the Equations
To find the values of C and T, we can use the method of elimination or substitution. Here, we will use elimination:
- From the first equation (3C + 2T = 1850), multiply everything by 3:
- 9C + 6T = 5550
- From the second equation (5C + 3T = 2850), multiply everything by 2:
- 10C + 6T = 5700
Now, we have two new equations:
1. 9C + 6T = 5550
2. 10C + 6T = 5700
Next, subtract the first equation from the second:
10C + 6T - (9C + 6T) = 5700 - 5550
C = 150
Now substitute C back into one of the original equations to find T:
3C + 2T = 1850
3(150) + 2T = 1850
450 + 2T = 1850
2T = 1400
T = 700
Calculating Total Cost
Now that we have the costs:
- Cost of one chair (C) = Rs. 150
- Cost of one table (T) = Rs. 700
The total cost of one chair and one table is:
C + T = 150 + 700 = Rs. 850
Conclusion
Thus, the total cost of one chair and one table is Rs. 850, which corresponds to option 'B'.
We have two equations based on the information provided about chairs and tables:
1. Equation from the first statement:
- 3 chairs + 2 tables = Rs. 1850
- Let the cost of one chair be C and one table be T.
- This gives us the equation: 3C + 2T = 1850
2. Equation from the second statement:
- 5 chairs + 3 tables = Rs. 2850
- This gives us the equation: 5C + 3T = 2850
Solving the Equations
To find the values of C and T, we can use the method of elimination or substitution. Here, we will use elimination:
- From the first equation (3C + 2T = 1850), multiply everything by 3:
- 9C + 6T = 5550
- From the second equation (5C + 3T = 2850), multiply everything by 2:
- 10C + 6T = 5700
Now, we have two new equations:
1. 9C + 6T = 5550
2. 10C + 6T = 5700
Next, subtract the first equation from the second:
10C + 6T - (9C + 6T) = 5700 - 5550
C = 150
Now substitute C back into one of the original equations to find T:
3C + 2T = 1850
3(150) + 2T = 1850
450 + 2T = 1850
2T = 1400
T = 700
Calculating Total Cost
Now that we have the costs:
- Cost of one chair (C) = Rs. 150
- Cost of one table (T) = Rs. 700
The total cost of one chair and one table is:
C + T = 150 + 700 = Rs. 850
Conclusion
Thus, the total cost of one chair and one table is Rs. 850, which corresponds to option 'B'.
Solve : 5x/2+3x/4>39/4, x ∈ R :- a)(-3, ∞)
- b)(3,3)
- c)(-∞,3)
- d)(3,∞)
Correct answer is option 'D'. Can you explain this answer?
Solve : 5x/2+3x/4>39/4, x ∈ R :
a)
(-3, ∞)
b)
(3,3)
c)
(-∞,3)
d)
(3,∞)
|
|
Aishwarya jain answered |
It is not clear what the expression is asking. Please provide more information or clarify the expression.
The pairs of equations x + 2y - 5 = 0 and -4x - 8y + 20 = 0 have:- a)Unique solution
- b)Exactly two solutions
- c)Infinitely many solutions
- d)No solution
Correct answer is option 'C'. Can you explain this answer?
The pairs of equations x + 2y - 5 = 0 and -4x - 8y + 20 = 0 have:
a)
Unique solution
b)
Exactly two solutions
c)
Infinitely many solutions
d)
No solution
|
|
Meera Rana answered |
a1/a2 = 1/-4
b1/b2 = 2/-8 = 1/-4
c1/c2 = -5/20 = -¼
This shows:
a1/a2 = b1/b2 = c1/c2
Therefore, the pair of equations has infinitely many solutions.
b1/b2 = 2/-8 = 1/-4
c1/c2 = -5/20 = -¼
This shows:
a1/a2 = b1/b2 = c1/c2
Therefore, the pair of equations has infinitely many solutions.
Solve : 2(x-1)/5<3(2+x)/7, x ∈ R :- a)(44, ∞)
- b)(44,-∞)
- c)(– 44,∞)
- d)(+ 44,∞)
Correct answer is option 'C'. Can you explain this answer?
Solve : 2(x-1)/5<3(2+x)/7, x ∈ R :
a)
(44, ∞)
b)
(44,-∞)
c)
(– 44,∞)
d)
(+ 44,∞)
|
|
Drishti Kumari answered |
2( x - 1 ) / 5 is less than 3 ( 2 + x ) / 7
2x - 2 / 5 is less than 6 + 3x / 7
Cross multiplication
14x - 14 is less than 30 + 15x
14 x - 15 x is less than 30 + 14
- x is less than 44
When we divide from negative no. to positive no. then inequality sign becomes change
So,
x is greater than - 44
On number line , it is ( - 44 , + infinity )
Hence, option (C) is correct .
2x - 2 / 5 is less than 6 + 3x / 7
Cross multiplication
14x - 14 is less than 30 + 15x
14 x - 15 x is less than 30 + 14
- x is less than 44
When we divide from negative no. to positive no. then inequality sign becomes change
So,
x is greater than - 44
On number line , it is ( - 44 , + infinity )
Hence, option (C) is correct .
Solve : x/5R : <(3x-2)/4-(5x-3)/5, x ∈ R:
- a)(2/7,∞)
- b)(2/9,∞)
- c)(-∞, 2/9)
- d)(∞, 2/9)
Correct answer is option 'C'. Can you explain this answer?
Solve : x/5R : <(3x-2)/4-(5x-3)/5, x ∈ R:
a)
(2/7,∞)
b)
(2/9,∞)
c)
(-∞, 2/9)
d)
(∞, 2/9)
|
|
Ram Mohith answered |
I think the question is to solve for x, x/5 < (3x - 2)/4 - (5x - 3)/5
Now multiply throughout with 20,
4x < 5(3x - 2) - 4(5x - 3)
4x < 15x - 10 - 20x + 12
20x - 15x + 4x < 12 - 10
9x < 2
x < 2/9
So, x can be any real number in the interval (-infinity, 2/9)
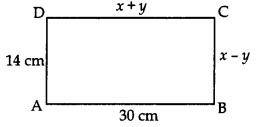
In Fig., ABCD is a rectangle. Find the values of x and y.
- a)22, 8
- b)20,10
- c)15, 9
- d)-22, -8
Correct answer is option 'A'. Can you explain this answer?
In Fig., ABCD is a rectangle. Find the values of x and y.


a)
22, 8
b)
20,10
c)
15, 9
d)
-22, -8

|
Kds Coaching answered |
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
The solution of the equations x - y = 2 and x + y = 4 is:- a)3 and 1
- b)4 and 3
- c)5 and 1
- d)-1 and -3
Correct answer is option 'A'. Can you explain this answer?
The solution of the equations x - y = 2 and x + y = 4 is:
a)
3 and 1
b)
4 and 3
c)
5 and 1
d)
-1 and -3

|
Kds Coaching answered |
To solve the equations, follow these steps:
- Start with the first equation: x - y = 2.
- Rearrange to express x in terms of y: x = y + 2.
- Substitute this expression for x into the second equation: x * y = 4.
- This gives: (y + 2) * y = 4.
- Expanding this results in: y^2 + 2y - 4 = 0.
- Now, use the quadratic formula to solve for y: y = (-b ± √(b² - 4ac)) / 2a, where a = 1, b = 2, and c = -4.
- Calculating the discriminant: b² - 4ac = 2² - 4(1)(-4) = 4 + 16 = 20.
- Thus, y = (-2 ± √20) / 2.
- Calculating the two possible values for y gives: y = 1 or y = -4.
- Substituting y = 1 back into x = y + 2 yields: x = 3.
- For y = -4, substituting gives: x = -2.
Therefore, the solutions are:
- x = 3 and y = 1.
- x = -2 and y = -4.
Chapter doubts & questions for Linear Equations in Two Variables - Mathematics Class 10 (Maharashtra SSC Board) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Linear Equations in Two Variables - Mathematics Class 10 (Maharashtra SSC Board) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily