All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Even, Odd, Positive and Negative Numbers for GMAT Exam
The product of the units, tens, and hundreds digits of the positive 3-digit integer x is 42. Is x even?(1) x is less than 300. ?(2) The tens digit of x is 7. ?- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'D'. Can you explain this answer?
The product of the units, tens, and hundreds digits of the positive 3-digit integer x is 42. Is x even?
(1) x is less than 300. ?
(2) The tens digit of x is 7. ?
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
Aditya Kumar answered |
Correct Answer :- d
Explanation : If the product of the three digits is 42 then the possible set of three digits is 2,3,7 or 6,7,1
Numbers from 2,3,7 are 237,273,327,372,723,732
Numbers from 6,7,1 are 167,176,617,671,716,761
Numbers less than 300 are 237,273,167,176 so x can be both even or odd- Insufficient.
Tens digit is 7
Numbers can be 273,372,671,176.. x can be both even and odd -Insufficient
Taking both the statements together
Number <300 and tens digit is 7 nos are 273,176 both even and odd possible so Insufficient
If p and q are integers and p + q + p is odd, which of the following must be odd?a) pb) qc) p+ qd) pq + pCorrect answer is option 'B'. Can you explain this answer?
|
Lavanya Menon answered |
q must be odd, e.g. follwing patterns;
2+1+2 = 5
1+3+1 = 5
1+2+1 = 4
2+4+2 = 8
Hence all combinations with an even q would yield even results, thus q must be odd.
2+1+2 = 5
1+3+1 = 5
1+2+1 = 4
2+4+2 = 8
Hence all combinations with an even q would yield even results, thus q must be odd.
Which of the following statements must be true?
I. The product of first 100 prime numbers is even
II. The sum of first 100 prime numbers is odd.
III. The sum of first five non-negative even numbers is divisible by both 4 and 5
- a)I only
- b)II only
- c)I and III only
- d)I and II only
- e)I, II and III
Correct answer is option 'E'. Can you explain this answer?
Which of the following statements must be true?
I. The product of first 100 prime numbers is even
II. The sum of first 100 prime numbers is odd.
III. The sum of first five non-negative even numbers is divisible by both 4 and 5
a)
I only
b)
II only
c)
I and III only
d)
I and II only
e)
I, II and III
|
Nikita Singh answered |
Let's analyze each statement:
**I. The product of the first 100 prime numbers is even.**
- The first 100 prime numbers include 2, which is an even number. Since multiplying any number by an even number results in an even number, the product of the first 100 prime numbers must be even.
- Therefore, Statement I is true.
- The first 100 prime numbers include 2, which is an even number. Since multiplying any number by an even number results in an even number, the product of the first 100 prime numbers must be even.
- Therefore, Statement I is true.
**II. The sum of the first 100 prime numbers is odd.**
- The first prime number is 2 (even), and the remaining 99 prime numbers are all odd. The sum of an even number and an odd number is odd. Since we have one even and 99 odd numbers, the sum will be even + odd (which is odd) + 98 odds (which makes the sum odd).
- Therefore, Statement II is true.
- The first prime number is 2 (even), and the remaining 99 prime numbers are all odd. The sum of an even number and an odd number is odd. Since we have one even and 99 odd numbers, the sum will be even + odd (which is odd) + 98 odds (which makes the sum odd).
- Therefore, Statement II is true.
**III. The sum of the first five non-negative even numbers is divisible by both 4 and 5.**
- The first five non-negative even numbers are 0, 2, 4, 6, and 8. Their sum is \(0 + 2 + 4 + 6 + 8 = 20\).
- 20 is divisible by both 4 and 5.
- Therefore, Statement III is true.
- The first five non-negative even numbers are 0, 2, 4, 6, and 8. Their sum is \(0 + 2 + 4 + 6 + 8 = 20\).
- 20 is divisible by both 4 and 5.
- Therefore, Statement III is true.
Since all three statements are true, the correct answer is:
**5. I, II, and III**
Is z even?1) z/2 is even2) 3z is even
a)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the question.Correct answer is option 'A'. Can you explain this answer?
|
Meera Rana answered |
(1) Z = 2 * even
=> z is even
Sufficient
(2) 3z = even
3 is odd
So z is even if z is an integer
But if z = 8/3
Not Sufficient
Answer - A
=> z is even
Sufficient
(2) 3z = even
3 is odd
So z is even if z is an integer
But if z = 8/3
Not Sufficient
Answer - A
If x and y are positive integers and x is odd, is xy even? (1) x3y = 6a3 + 23 where a is a positive integer
(2) x2+y = 3k + 7 where k is a positive integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
If x and y are positive integers and x is odd, is xy even?
(1) x3y = 6a3 + 23 where a is a positive integer
(2) x2+y = 3k + 7 where k is a positive integer
(2) x2+y = 3k + 7 where k is a positive integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Avantika Dey answered |
Given: x and y are positive integers and x is odd
To find: Is xy even?
Statement 1: x^3y = 6a^3 * 23 where a is a positive integer
- We can factor x^3y as x * x^2 * y
- Since x is odd, x^2 is odd as well
- 6a^3 * 23 is an odd number because 6 is even and 23 is odd
- Therefore, x * x^2 * y * (6a^3 * 23) is even
- Thus, xy is even
- Statement 1 alone is sufficient to answer the question
Statement 2: x^2y = 3k * 7 where k is a positive integer
- We can factor x^2y as x^2 * y
- Since x is odd, x^2 is odd as well
- 3k * 7 is an odd number because 3 is odd and 7 is odd
- Therefore, x^2 * y * (3k * 7) is odd
- Thus, we cannot determine if xy is even or odd
- Statement 2 alone is not sufficient to answer the question
Since statement 1 alone is sufficient to answer the question, the correct answer is (A).
To find: Is xy even?
Statement 1: x^3y = 6a^3 * 23 where a is a positive integer
- We can factor x^3y as x * x^2 * y
- Since x is odd, x^2 is odd as well
- 6a^3 * 23 is an odd number because 6 is even and 23 is odd
- Therefore, x * x^2 * y * (6a^3 * 23) is even
- Thus, xy is even
- Statement 1 alone is sufficient to answer the question
Statement 2: x^2y = 3k * 7 where k is a positive integer
- We can factor x^2y as x^2 * y
- Since x is odd, x^2 is odd as well
- 3k * 7 is an odd number because 3 is odd and 7 is odd
- Therefore, x^2 * y * (3k * 7) is odd
- Thus, we cannot determine if xy is even or odd
- Statement 2 alone is not sufficient to answer the question
Since statement 1 alone is sufficient to answer the question, the correct answer is (A).
Can you explain the answer of this question below:Set S is given as S = {1,3,5,7,9,11,13,15,17}. In how many ways can three numbers be chosen from Set S such that the sum of those three numbers is 18?
- A:
0
- B:
1
- C:
2
- D:
3
- E:
4
The answer is a.
Set S is given as S = {1,3,5,7,9,11,13,15,17}. In how many ways can three numbers be chosen from Set S such that the sum of those three numbers is 18?
0
1
2
3
4
|
Princi Aggarwal answered |
Set s has only odd numbers
sum of three odd numbers is always an even number
hence it is not possible in any way
sum of three odd numbers is always an even number
hence it is not possible in any way
If m is an integer, is m odd?1) m/2 is not an even integer2) m – 3 is not an even integer- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
If m is an integer, is m odd?
1) m/2 is not an even integer
2) m – 3 is not an even integer
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Tanvi Deshpande answered |
The second statement is incomplete and does not provide any information about the parity of m.
Statement 1: If m/2 is not an even integer, then m must be an odd integer. This statement alone is sufficient to answer the question, as it confirms that m is indeed odd.
Statement 2: This statement is incomplete and cannot be used to determine the parity of m.
Therefore, the answer is A) Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Statement 1: If m/2 is not an even integer, then m must be an odd integer. This statement alone is sufficient to answer the question, as it confirms that m is indeed odd.
Statement 2: This statement is incomplete and cannot be used to determine the parity of m.
Therefore, the answer is A) Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Is the positive integer p even?(1) p^2 + p is even.(2) 4p + 2 is even.a)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'D'. Can you explain this answer?
|
|
Rhea Gupta answered |
**Statement 1:** p^2 is even
**Statement 2:** 4p is even
To determine if the positive integer p is even, we need to consider both statements together.
**Analysis:**
1. **Statement 1:** p^2 is even
- If p^2 is even, it implies that p is even because the square of an odd number is odd, and the square of an even number is even.
- Therefore, statement 1 alone is sufficient to conclude that p is even.
2. **Statement 2:** 4p is even
- The product of any integer and an even number is always even.
- Therefore, statement 2 alone is sufficient to conclude that p is even.
Since each statement individually is enough to determine that p is even, the correct answer is **option C** - Each statement can answer the question individually.
**Explanation:**
Both statements provide sufficient information to determine that p is even.
- From statement 1, if p^2 is even, it means p must be even, as the square of an odd number is odd and the square of an even number is even. Therefore, statement 1 alone is enough to conclude that p is even.
- Similarly, from statement 2, if 4p is even, it means that p must be even because the product of any integer and an even number is always even.
Since each statement individually provides enough information to determine that p is even, additional information is not required. Therefore, option D is incorrect.
Hence, the correct answer is **option C** - Each statement can answer the question individually.
**Statement 2:** 4p is even
To determine if the positive integer p is even, we need to consider both statements together.
**Analysis:**
1. **Statement 1:** p^2 is even
- If p^2 is even, it implies that p is even because the square of an odd number is odd, and the square of an even number is even.
- Therefore, statement 1 alone is sufficient to conclude that p is even.
2. **Statement 2:** 4p is even
- The product of any integer and an even number is always even.
- Therefore, statement 2 alone is sufficient to conclude that p is even.
Since each statement individually is enough to determine that p is even, the correct answer is **option C** - Each statement can answer the question individually.
**Explanation:**
Both statements provide sufficient information to determine that p is even.
- From statement 1, if p^2 is even, it means p must be even, as the square of an odd number is odd and the square of an even number is even. Therefore, statement 1 alone is enough to conclude that p is even.
- Similarly, from statement 2, if 4p is even, it means that p must be even because the product of any integer and an even number is always even.
Since each statement individually provides enough information to determine that p is even, additional information is not required. Therefore, option D is incorrect.
Hence, the correct answer is **option C** - Each statement can answer the question individually.
Each digit in the two-digit number G is halved to form a new two-digit number H. Which of the following could be the sum of G and H? ?- a)153
- b)150
- c)129
- d)89
Correct answer is option 'C'. Can you explain this answer?
Each digit in the two-digit number G is halved to form a new two-digit number H. Which of the following could be the sum of G and H? ?
a)
153
b)
150
c)
129
d)
89
|
Dhruv Mehra answered |
Two-step solution:
G + G/2 = 3G/2 --> the sum is a multiple of 3.
G is a two-digit number --> G < 100 --> 3G/2 < 150.
Among the answer choices the only multiple of 3 which is less than 150 is 129.
If i and j are integers, is i + j even?1) i < 102) i = ja)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the question.Correct answer is option 'A'. Can you explain this answer?
|
Nilotpal Sen answered |
1) I < 10
IF... I = 9 and J = 1, then the answer to the question is YES.
I = 9 and J = 2, then the answer to the question is NO.
Fact 1 is INSUFFICIENT
2) I = J
Fact 2 tells us that I and J are the SAME integer, so (I+J) can be rewritten as either 2I or 2J. Since the product of any integer and 2 results in an EVEN integer, the answer to the question is ALWAYS YES. You can also prove it with examples:
I = 1 and J = 1 ... total = 2
I = 2 and J = 2 ... total = 4
I = 3 and J = 3 ... total = 6
Etc.
Fact 2 is SUFFICIENT
If x and y are both integers, is xy even?
1) x + y is odd
2) x is even
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
If x and y are both integers, is xy even?
1) x + y is odd
2) x is even
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Meera Rana answered |
Correct Answer :- C
Explanation : In order the product of two integers to be even either (or both) of them must be even. So, the question basically asks whether either x or y is even.
(1) x = y + 1. If x is odd then y is even and vise-versa. Sufficient.
(2) x is even
Let x = 2, y= 3
x*y = 2*3 = 6 (Even), Sufficient
If x, y, and z are positive integers, where x is an odd number and z = x2 + y2 + 4. Is y2 divisible by 4?(1) Z = 8k -3 where k is a positive integer (2) When (z-x+1) is divided by 2, it leaves a remainder.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
If x, y, and z are positive integers, where x is an odd number and z = x2 + y2 + 4. Is y2 divisible by 4?
(1) Z = 8k -3 where k is a positive integer
(2) When (z-x+1) is divided by 2, it leaves a remainder.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Nikita Singh answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that x, y and z are positive integers.
Also, x is odd
And,
z= x2 + y2 + 4
By rearranging the terms, we get:
y2 = z – x2 – 4 …………. (1)
The question asks us whether y2 is divisible by 4 or not. If y is divisible by 2, then y2 will be divisible by 4; else it will not be.
And if y is divisible by 2, this means that y is even.
Thus, the question is indirectly asking us: is y even?
y will be even if the right hand side of Equation 1 is even. So, let’s analyze the condition in which this will be so.
Now, we are given that x is an odd number. This means that x2 is also odd (Odd * Odd = Odd)
So, in the part (x2 – 4), we are subtracting an even number from an odd number. Think of what happens when we subtract 4 from 9. We get 5, which is an odd number. So, here too, the result of subtracting 4 from x2 will be an Odd number (Please note that the result may be positive or negative. We are not concerned with that. All that we want to know is whether the result will be even or odd)
So, from Equation 1 we get:
y2 = z – Odd number . . . (2)
Now,
Even +/-Odd = Odd (Think: 4 + 1 = 5)
And, Odd +/-Odd = Even (Think: 3 + 1 = 4)
Thus, from equation (2)
It is clear that y2 will be even only if z is an odd number
- y will be even only if z is an odd number
- Our task is to determine if z is odd or not.
Step 3: Analyze Statement 1
Statement (1) says:
z = 8*k – 3
Now, irrespective of whether k is even or odd,
8 * k = even number
ð 8k – 3 = Even number -odd number = Odd Number (Think: 8 – 3 = 5)
So, the analysis of statement (1) tells us that z is an odd number.
Since we have been able to determine that z is an odd number, this means that y is an even number.
Thus, Statement (1) alone is sufficient to answer the question: is y even?
Step 4: Analyze Statement 2
When the expression (z-x+1) is divided by 2, we get a remainder. This tells us that (z-x+1) is an odd number. So,
z – x + 1 = odd
This means that,
z – x = Odd number – 1 = Odd number – odd number = Even number (Think: 5 – 3 = 2)
So, z = x + Even number
Now, we are given that x is an odd number
So, z = Odd number + Even number = Odd number (Think: 1 + 2 = 3)
Thus, z is an odd number
- y is an even number
Thus, Statement 2 alone is sufficient to answer the question: is y even?
Step 5: Analyze Both Statements Together (if needed)
Since we got unique answers in step 3 and 4, so this step is not required
Answer: Option (D)
If m and n are integers, is m odd??1) m + n is odd2) m + n = n^2 + 5a)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'D'. Can you explain this answer?
|
|
Gauri Iyer answered |
(1) n + m is odd
The sum of two integers is odd only if one is odd and another is even, hence m may or may not be odd. Not sufficient.
(2) n + m = n2 + 5
(2) n + m = n2 + 5
--> m−5=n2−n
=> m−5=n(n−1)
either n or n−1 is even hence n(n−1)=even
=> n(n−1)=even
=> m−5=m−odd=even
--> m=odd. Sufficient.
The product of integers x, y, and z is even. Is z even? 1) x/y = z2) z = xy- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
The product of integers x, y, and z is even. Is z even?
1) x/y = z
2) z = xy
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Dhruv Mehra answered |
The product of integers x,y, and z is even, is z even?
1. X/Y = Z
2. Z=XY
x*y*z = 2k, where k is an integer
At least one of them is even
1. X/Y = Z
if x = 6, y = 2, then z = 3, not even
if x = 6, y = 3, then z = 2, even
2. Z=XY
so (z)^2 = 2*k (because x*y*z = 2k, where k is an integer)
Sufficient, as if square of an integer is even ,then the integer is even
For all positive integers m, (m) = 3m when m is odd and (m) = (1⁄2) m when m is even, which of the following is equivalent to (9)*(6)? - a)(81)
- b)(54)
- c)(36)
- d)(27)
Correct answer is option 'D'. Can you explain this answer?
For all positive integers m, (m) = 3m when m is odd and (m) = (1⁄2) m when m is even, which of the following is equivalent to (9)*(6)?
a)
(81)
b)
(54)
c)
(36)
d)
(27)
|
|
Pallavi Choudhury answered |
Notice that [ ] is just some function such that "[m]=3m when m is odd and [m]=(1/2)*m when m is even".
So, [m]=3m when m is odd, [m]=(1/2)*m when m is even.
As 9 is odd then [9] equals to 3*9=27;
As 6 is even then [6] equals to 1/2*6=3;
So [9]*[6]=27*3=81. Note that numbers in the answer choices are also in boxes, so we have: [m]=81. m could be 27 (in this case as 27 is odd [27]=3*27=81) OR 162 (in this case as 162 is even [162]=162/2=81) --> only [27] is in the answer choices.
So, [m]=3m when m is odd, [m]=(1/2)*m when m is even.
As 9 is odd then [9] equals to 3*9=27;
As 6 is even then [6] equals to 1/2*6=3;
So [9]*[6]=27*3=81. Note that numbers in the answer choices are also in boxes, so we have: [m]=81. m could be 27 (in this case as 27 is odd [27]=3*27=81) OR 162 (in this case as 162 is even [162]=162/2=81) --> only [27] is in the answer choices.
If x, y, z and w are positive integers, is x odd?(1) 7x + 8y + 4z + 5w is odd
(2) 3x + 2y + 8z + 2w is even- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If x, y, z and w are positive integers, is x odd?
(1) 7x + 8y + 4z + 5w is odd
(2) 3x + 2y + 8z + 2w is even
(2) 3x + 2y + 8z + 2w is even
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Priyanshu Negi answered |
NOTE. addition OF EVEN NO. RESULTS IN AN EVEN NO.
In statement 1. 7x+8y+4z+5w is odd here, which means the values of 8y,4z are even as multiple of 8 and 4 are even and the addition of these 5 terms results in an odd no.
it concludes that either 7x is odd or 5w is odd
as any no. multiplied by 7 is either even or odd Same is the case with 5w , so we can say that the whole complete value of the term depends upon the value of 5w (being odd or even)
In Statement 2. 3x+2y+8z+2w is even .
here terms , 2y,8z,2w are even as any no. multiplied by 2 and 8 or results in an even no.
So, if the whole expression is even 3x neends to be even which means x is even and multiple of 3x is also even
Result . X is an even no. hence Option B is correct
In statement 1. 7x+8y+4z+5w is odd here, which means the values of 8y,4z are even as multiple of 8 and 4 are even and the addition of these 5 terms results in an odd no.
it concludes that either 7x is odd or 5w is odd
as any no. multiplied by 7 is either even or odd Same is the case with 5w , so we can say that the whole complete value of the term depends upon the value of 5w (being odd or even)
In Statement 2. 3x+2y+8z+2w is even .
here terms , 2y,8z,2w are even as any no. multiplied by 2 and 8 or results in an even no.
So, if the whole expression is even 3x neends to be even which means x is even and multiple of 3x is also even
Result . X is an even no. hence Option B is correct
If x and y are positive integers, is the product xy even?1)5x - 4y is even2)6x + 7y is evena)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'C'. Can you explain this answer?
|
|
Manasa Gupta answered |
1) 4y will always be even. Then we have 5x−even=even ,
For this to be the case, 5x must be even. Since 5 can't be even, then x must be even. Thus the product xy will be even. Sufficient.
2) 6x will always be even. Then we have even+7y=even.
2) 6x will always be even. Then we have even+7y=even.
Thus 7y is even, and y is even, and xy is even. Sufficient.
If a , b, and c are integers and ab2 / c is a positive even integer, which of the following must be true?I. ab is even II. ab > 0 III. c is even?- a)I only
- b)II only
- c)I and III only
- d)I, II, and III
Correct answer is option 'A'. Can you explain this answer?
If a , b, and c are integers and ab2 / c is a positive even integer, which of the following must be true?
I. ab is even
II. ab > 0
III. c is even?
a)
I only
b)
II only
c)
I and III only
d)
I, II, and III
|
|
Aditya Kumar answered |
Given: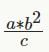 
= even > 0 ab2 = c* even = even--> either a is even or b or both.
I. ab is even --> according to the above this must be true;
II. ab > 0 --> not necessarily true, bb could be positive as well as negative (for example a=1, c = 1 and b =−2);
III. c is even --> not necessarily true, see above example.
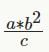= even > 0 ab2 = c* even = even--> either a is even or b or both.I. ab is even --> according to the above this must be true;
II. ab > 0 --> not necessarily true, bb could be positive as well as negative (for example a=1, c = 1 and b =−2);
III. c is even --> not necessarily true, see above example.
If A is a positive integer, then which of the following statements is true?1. A2 + A -1 is always even. 2. (A4+1)(A4+2) + 3A is even only when A is even. 3. (A-1)(A+2)(A+4) is never odd. - a)1
- b)2
- c)3
- d)1 and 2
- e)2 and 3
Correct answer is option 'E'. Can you explain this answer?
If A is a positive integer, then which of the following statements is true?
1. A2 + A -1 is always even.
2. (A4+1)(A4+2) + 3A is even only when A is even.
3. (A-1)(A+2)(A+4) is never odd.
a)
1
b)
2
c)
3
d)
1 and 2
e)
2 and 3
|
|
Aarav Sharma answered |
Step 1: Question statement and Inferences
We are given that A is a positive integer. A may be odd or even.
Step 2: Analyzing the given statements
1. A2 + A -1 is always even
Case (i) A is Odd
- A2 is also odd (Odd × Odd = Odd)
- A2 + A is even (Odd + Odd = Even)
- A2 + A -1 is odd ( Even – Odd = Odd)
We don’t even need to consider the case when A is even, because Statement 1 has already been proven FALSE.
2. (A4+1)(A4+2) + 3A is even only when A is even
Case (i): A is odd
- 3A is odd (Odd × Odd = Odd)
Now, an odd number multiplied with itself any number of times will give an odd product
- A4 is odd
- A4 + 1 is even (Odd + Odd = Even)
- A4 + 2 is odd (Odd + Even = Odd)
- (A4+1)(A4+2) + 3A = Even × Odd + Odd
- (A4+1)(A4+2) + 3A = Even + Odd
- (A4+1)(A4+2) + 3A = Odd
Thus, when A is odd, (A4+1)(A4+2) + 3A is odd
Case (ii): A is even
3A is even (Odd × Even = Even)
An even number multiplied with itself any number of times will give an even product
- A4 is even
- A4 + 1 is odd (Even + Odd = Odd)
- A4 + 2 is even (Even + Even = Even)
- (A4+1)(A4+2) + 3A = Odd × Even + Even
- (A4+1)(A4+2) + 3A = Even + Even
- (A4+1)(A4+2) + 3A = Even
Thus, when A is even, (A4+1)(A4+2) + 3A is even
Thus, Statement 2 is TRUE.
3. (A-1)(A+2)(A+4) is never odd
Case (i): A is odd
- A-1 is even (Odd -Odd = Even)
- A + 2 is odd (Odd + Even = Odd)
- A + 4 is odd (Odd + Even = Odd)
- (A-1)(A+2)(A+4) = Even × Odd × Odd
- (A-1)(A+2)(A+4) = Even
Thus, when A is odd, (A-1)(A+2)(A+4) is even
Case (ii): A is even
- A-1 is odd (Even -Odd = Odd)
- A + 2 is even (Even + Even = Even)
- A + 4 is even (Even + Even = Even)
- (A-1)(A+2)(A+4) = Odd × Even × Even
- (A-1)(A+2)(A+4) = Even
Thus, when A is even, (A-1)(A+2)(A+4) is even
Thus, Statement 3 is TRUE.
Answer: Option (E)
If n is an integer, is n even?1) n^2 – 1 is an odd integer2) 3n + 4 is an even integera)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'C'. Can you explain this answer?
|
|
Rhea Gupta answered |
**Statement 1:** n^2 – 1 is an odd integer
If n^2 – 1 is an odd integer, it means that n^2 must be an even integer. The difference between an odd integer and an even integer is always odd. Therefore, if n^2 is even, it implies that n must be even.
**Statement 2:** 3n + 4 is an even integer
If 3n + 4 is an even integer, it means that 3n must be an even integer. An even integer multiplied by any other integer (in this case, 3) will also be even. Therefore, if 3n is even, it implies that n must be even.
Both statements individually provide sufficient information to determine that n is even. Therefore, each statement can answer the question individually.
The reason why option C is the correct answer is that each statement provides conclusive evidence that n is even. This means that even if we only have one of the statements, we can still determine that n is even. Therefore, both statements are individually sufficient to answer the question.
In conclusion, option C is correct because each statement can answer the question individually and provide enough information to determine that n is even.
If n^2 – 1 is an odd integer, it means that n^2 must be an even integer. The difference between an odd integer and an even integer is always odd. Therefore, if n^2 is even, it implies that n must be even.
**Statement 2:** 3n + 4 is an even integer
If 3n + 4 is an even integer, it means that 3n must be an even integer. An even integer multiplied by any other integer (in this case, 3) will also be even. Therefore, if 3n is even, it implies that n must be even.
Both statements individually provide sufficient information to determine that n is even. Therefore, each statement can answer the question individually.
The reason why option C is the correct answer is that each statement provides conclusive evidence that n is even. This means that even if we only have one of the statements, we can still determine that n is even. Therefore, both statements are individually sufficient to answer the question.
In conclusion, option C is correct because each statement can answer the question individually and provide enough information to determine that n is even.
If x is an integer, is x/2 an even integer? 1) x is divisible by 22) x is divisible by 4- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
If x is an integer, is x/2 an even integer?
1) x is divisible by 2
2) x is divisible by 4
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Dipanjan Mehra answered |
Explanation:
To determine whether x/2 is an even integer, we need to know whether x is even or odd.
Statement 1:
If x is divisible by 2, then x is even. Therefore, x/2 is also an integer (since it is half of an even integer), and it is also even (since dividing an even integer by 2 always results in an even integer).
This statement alone is sufficient to answer the question.
Statement 2:
If x is divisible by 4, then x is even. However, just because x is even does not mean that x/2 is even. For example, if x = 6, then x/2 = 3, which is odd.
This statement alone is not sufficient to answer the question.
Answer:
Therefore, the answer is option A: Exactly one of the statements can answer the question. Statement 1 alone is sufficient to answer the question, while statement 2 alone is not.
To determine whether x/2 is an even integer, we need to know whether x is even or odd.
Statement 1:
If x is divisible by 2, then x is even. Therefore, x/2 is also an integer (since it is half of an even integer), and it is also even (since dividing an even integer by 2 always results in an even integer).
This statement alone is sufficient to answer the question.
Statement 2:
If x is divisible by 4, then x is even. However, just because x is even does not mean that x/2 is even. For example, if x = 6, then x/2 = 3, which is odd.
This statement alone is not sufficient to answer the question.
Answer:
Therefore, the answer is option A: Exactly one of the statements can answer the question. Statement 1 alone is sufficient to answer the question, while statement 2 alone is not.
If k and y are integers, and 10k + y is odd, which of the following must be true?a)k is oddb)k is evenc)y is oddd)both k and y are oddCorrect answer is option 'C'. Can you explain this answer?
|
|
Arka Basu answered |
Explanation:
To determine which of the given statements must be true, let's analyze the information provided and the possible scenarios:
Given:
- k and y are integers
- 10k + y is odd
Scenario 1: k is odd
- If k is odd, it can be represented as k = 2n + 1, where n is an integer.
- Substituting k in the expression 10k + y, we get 10(2n + 1) + y = 20n + 10 + y = 2(10n + 5) + y = 2m + y, where m = 10n + 5 is an integer.
- Since 2m is even, the sum 2m + y can only be odd if y is odd.
- Therefore, if k is odd, y must be odd.
Scenario 2: k is even
- If k is even, it can be represented as k = 2n, where n is an integer.
- Substituting k in the expression 10k + y, we get 10(2n) + y = 20n + y = 2(10n) + y = 2m + y, where m = 10n is an integer.
- In this case, the sum 2m + y can be odd or even depending on the value of y.
- Therefore, if k is even, y can be either odd or even.
Conclusion:
From the analysis of the two scenarios, we can conclude that the only statement that must be true is:
c) y is odd
This is because if 10k + y is odd, y must be odd in order to make the sum odd, regardless of whether k is odd or even.
Therefore, option 'C' is the correct answer.
To determine which of the given statements must be true, let's analyze the information provided and the possible scenarios:
Given:
- k and y are integers
- 10k + y is odd
Scenario 1: k is odd
- If k is odd, it can be represented as k = 2n + 1, where n is an integer.
- Substituting k in the expression 10k + y, we get 10(2n + 1) + y = 20n + 10 + y = 2(10n + 5) + y = 2m + y, where m = 10n + 5 is an integer.
- Since 2m is even, the sum 2m + y can only be odd if y is odd.
- Therefore, if k is odd, y must be odd.
Scenario 2: k is even
- If k is even, it can be represented as k = 2n, where n is an integer.
- Substituting k in the expression 10k + y, we get 10(2n) + y = 20n + y = 2(10n) + y = 2m + y, where m = 10n is an integer.
- In this case, the sum 2m + y can be odd or even depending on the value of y.
- Therefore, if k is even, y can be either odd or even.
Conclusion:
From the analysis of the two scenarios, we can conclude that the only statement that must be true is:
c) y is odd
This is because if 10k + y is odd, y must be odd in order to make the sum odd, regardless of whether k is odd or even.
Therefore, option 'C' is the correct answer.
Set P consists of the first n positive multiples of 3 and set Q consists of the first m positive multiples of 5. The sum of all the numbers in set P is equal to R and the sum of all the numbers in set Q is equal to S. If m and n are positive integers, is the difference between R and S odd?(1) m is odd and n is even(2) m can be expressed in the form of 4x +3 and n can be expressed in the form of 2x, where x is a positive integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Set P consists of the first n positive multiples of 3 and set Q consists of the first m positive multiples of 5. The sum of all the numbers in set P is equal to R and the sum of all the numbers in set Q is equal to S. If m and n are positive integers, is the difference between R and S odd?
(1) m is odd and n is even
(2) m can be expressed in the form of 4x +3 and n can be expressed in the form of 2x, where x is a positive integer
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Sravya Joshi answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Difference of two integers will be odd, only if one of the numbers is odd.
- Let’s see when R and S will be odd:
- The even-odd nature of R will depend on the values of n and n + 1. Since n and n+ 1 are consecutive integers, only one of them can be even.
- Now, in the expression of R as n(n+1) is divided by 2, for R to be even, either of n or n + 1 should be a multiple of 4, i.e. they should be of the form 4k, where k is a positive integer. Hence, following cases arise:
- n is of the form 4k, i.e. n = 4k OR
- n+1 is of the form 4k, i.e. n + 1 = 4k
- So, n = 4k – 1 = 4(k -1) + 4 -3 = 4(k-1) + 3
- So, we can say that R will be even if n is of the form 4k or 4k + 3. For all the other cases, R will be odd
- Since the expression of S is similar to R, we can say that S will be even if m is of the form 4k or 4k + 3
- So, we need to look for values of m and n in the statements.
Step 3: Analyze Statement 1 independently
(1) m is odd and n is even
- As we do not know if m or n is of the form of 4k or 4k + 3, we cannot say, if R and S are odd or even.
- Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) m can be expressed in the form of 4x +3 and n can be expressed in the form of 2x, where x is a positive integer
- As m can be expressed in the form of 4x + 3, S will be even.
- As n can be expressed in the form of 2x, n may be expressed in the form of 4x or may not be expressed in the form of 4x.
- So, R may be odd or R may be even.
- If R is odd, R – S = odd
- If R is even, R – S = even.
- So, R may be odd or R may be even.
- Hence, we cannot say for sure if R – S is odd.
- Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
(1) From statement-1, we know that is odd and n is even
(2) From statement-2, we know that R may be even or odd and S is even
- Combining both the statements does not tell us anything about the even-odd nature of R, hence we cannot say for sure if R – S = odd.
- Insufficient to answer.
Answer: E
If positive integers x and y are not both odd, which of the following must be even?
- a)x + y
- b)x - y
- c)xy
- d)2(x y) - 1
Correct answer is option 'C'. Can you explain this answer?
If positive integers x and y are not both odd, which of the following must be even?
a)
x + y
b)
x - y
c)
xy
d)
2(x y) - 1
|
|
Meera Rana answered |
Positive integers x and y are NOT both odd, means that either both x and y are even or one is even and the other one is odd. In either case xy must be even.
If x and y are integers, is x (y + 1) an even number?1)xand y are prime numbers.
2)y > 7 ?
a)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'B'. Can you explain this answer?
2)y > 7 ?
a)Exactly one of the statements can answer the question
|
|
Sinjini Mukherjee answered |
1) If x and y are prime numbers, then x(y-1) can be either even or odd. For example, if x is 2 and y is 3, then x(y-1) = 2(3-1) = 4, which is even. However, if x is 3 and y is 5, then x(y-1) = 3(5-1) = 12, which is also even. Therefore, this statement alone is insufficient to determine if x(y-1) is even or odd.
2) If y is odd, then y-1 is even. In this case, x(y-1) will always be even, regardless of the value of x. For example, if y is 5, then y-1 is 4, and x(y-1) will always be even for any integer value of x. Therefore, this statement alone is sufficient to determine that x(y-1) is always even.
Combining both statements, we have conflicting information. Statement 1 tells us that x(y-1) can be either even or odd, while statement 2 tells us that x(y-1) is always even if y is odd. Therefore, the answer is not determinable.
2) If y is odd, then y-1 is even. In this case, x(y-1) will always be even, regardless of the value of x. For example, if y is 5, then y-1 is 4, and x(y-1) will always be even for any integer value of x. Therefore, this statement alone is sufficient to determine that x(y-1) is always even.
Combining both statements, we have conflicting information. Statement 1 tells us that x(y-1) can be either even or odd, while statement 2 tells us that x(y-1) is always even if y is odd. Therefore, the answer is not determinable.
Is p2 an odd integer?1) p is an odd integer2) √p is an odd integer- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c)Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
Is p2 an odd integer?
1) p is an odd integer
2) √p is an odd integer
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Arka Basu answered |
P + 2 is an even integer
Statement 1 alone is not sufficient to determine whether p2 is an odd integer or not.
Statement 2 alone is not sufficient to determine whether p2 is an odd integer or not.
Combining both statements, we have p + 2 is an even integer. Since p is an odd integer, adding 2 to an odd integer will always result in an odd integer. Therefore, p2 is an odd integer.
Therefore, the answer is C) Statements 1 and 2 together are sufficient to answer the question.
Statement 1 alone is not sufficient to determine whether p2 is an odd integer or not.
Statement 2 alone is not sufficient to determine whether p2 is an odd integer or not.
Combining both statements, we have p + 2 is an even integer. Since p is an odd integer, adding 2 to an odd integer will always result in an odd integer. Therefore, p2 is an odd integer.
Therefore, the answer is C) Statements 1 and 2 together are sufficient to answer the question.
If X is a positive integer, is X2 + 1 an odd number?(1) X is the smallest integer that is divisible by all integers from 11 to 15, inclusive.(2) 3X is an odd number.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is 'A'. Can you explain this answer?
If X is a positive integer, is X2 + 1 an odd number?
(1) X is the smallest integer that is divisible by all integers from 11 to 15, inclusive.
(2) 3X is an odd number.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Aarav Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
For X2 + 1 to be odd
--> X2 must be even
--> X must be even
We need to find if X is even or not
Step 3: Analyze Statement 1
X is the smallest integer that is divisible by all integers from 11 to 15, inclusive
--> X is divisible by 12 and 14
--> X is even
Sufficient.
Step 4: Analyze Statement 2
3X is an odd number
An odd number multiplied with itself any number of times will give an odd product
--> 3X will always be odd, whether X is even or odd
Not Sufficient.
Step 5: Analyze Both Statements Together (if needed)
We get a unique answer in step 3, so this step is not required
Answer: Option (A)
What is the ration of number of odd integers to the number of even integers between -10.5 and 10.5?- a)9/10
- b)10/11
- c)11/12
- d)20/21
Correct answer is option 'B'. Can you explain this answer?
What is the ration of number of odd integers to the number of even integers between -10.5 and 10.5?
a)
9/10
b)
10/11
c)
11/12
d)
20/21
|
|
Anaya Patel answered |
Integers between -10.5 and 10.5 are
-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Odd integers are -9, -7, -5, -3, -1, 1, 3, 5, 7, 9 (Total 10)
Even integers are -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10 (Total 11)
Hence, ratio of number of odd integers to the number of even integers between -10.5 and 10.5 is 10/11
If a, b, and k are positive integers, is the sum (a + b) an even number or an odd number?(1) a = ( k3 + 3k2 + 3k + 6) (2) b = (k2 + 4a +5) - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
If a, b, and k are positive integers, is the sum (a + b) an even number or an odd number?
(1) a = ( k3 + 3k2 + 3k + 6)
(2) b = (k2 + 4a +5)
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Aarav Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that a, b, and k are positive integers. And, we have to find out whether the sum of a and b will be even or odd.
Let us draw a table for all the possible cases for the even-odd property of a and b, and the corresponding property of the sum (a+b):
Thus we see that:
If a and b are both odd or both even, then the sum (a+b) will be even
If a and b are both odd or both even, then the sum (a+b) will be even
But if one out of a and b is even, and the other is odd, the sum (a+b) will be odd.
So, we will need to determine the even-odd property of both a and b in order to be in a position to say whether the sum (a+b) is odd or even.
Step 3: Analyze Statement 1
Let’s analyze statement I:
a = k3 + 3k2 + 3k + 6
As we can see the value of a depends on the value of k. There can be two cases for the value of k – k can be either odd or even:
1. If k is odd:
This means, k3 = Odd (Odd*Odd*Odd = Odd; Think: 3*3*3 = 27)
Similarly, k2 will also be odd
So, 3k2 = Odd (Since 3 is odd and Odd*Odd = Odd)
Also, 3k = Odd
So, we get that
a = Odd number + odd number + odd number + even number
Think of easier numbers of the type of the right hand side of the above equation:
1 + 1 + 1 + 2 = 5, which is odd
This means that the RHS of the above equation will be an odd number
So, a is an odd number
So, if k is an odd number, a will be an odd number.
2. If k is even:
This means, k3 = Even (Even*Even*Even = Even; Think: 2*2*2 = 8)
Similarly, k2 will also be even
So, 3k2 = Even (Odd*Even = Even)
Also, 3k = Even
So, we get that
a = Even number + even number + even number + even number = Even number
So, a is an even number
Thus, if k is an even number, “a” will be an even number.
To conclude,
If k is odd => a is odd
If k is even => a is even
Thus, the value of a can be even or odd, depending on the value of k. This step fails to give us a definite answer whether a is an even number or odd number. Also, it does not give us any information about the values of b.
So, we can’t determine whether the expression a + b will be even or odd.
So, Statement 1 alone is not sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
Moving on, let’s analyze statement II:
b = (k2 + 4a +5) …………… (2)
Now, the value of b depends on the values of a and k.
If the values of a and k are independent of each other, then, we will have to consider 4 cases for the value of b:
Thus, we see that:
i) When k is even, b is odd
ii) When k is odd, b is even
iii) The even-odd property of b doesn’t depend on the value of a
Now, it is possible that the values of k and a are dependent on one another.
For example, if you were given that k = 8a
This would mean that irrespective of whether a is even or odd, k will always be even.
In that case, you would have been able to determine for sure that b will always be odd (though you would still be clueless about whether a is odd or even).
Or, if you were given that a = 8k, you would have been able to determine that a is even no matter what the value of k.
We are not given any information about the relationship, if any, between k and a. Neither are we given any other clue about the even-odd property of a.
Since this statement doesn’t tell us whether:
i) k is even or odd
ii) a is even or odd
iii) a and k are independent or not,
we will not be able to determine whether the sum (a+b) is even or odd.
So, Statement 2 alone is not sufficient to arrive at a unique answer
Step 5: Analyze Both Statements Together (if needed)
Since the individual analysis of the statements does not yield us any significant result, let’s analyse both of them together:
From Statement 1:
If k is odd => a is odd
If k is even => a is even
From Statement 2:
When k is even, b is odd
When k is odd, b is even
Combining the two statements, we get the following table:
Thus, we see that irrespective of the value of k, the sum (a+b) is always odd.
Thus, we have been able to arrive at a unique solution by combining the two statements.
Answer: Option (C)
Set A consists of a set of n consecutive integers. Is the sum of all the integers in set A even?(1) If -5 is added to set A, the set would become symmetric about 0(2) If the largest integer of set A is removed, the sum of the remaining integers is even- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
Set A consists of a set of n consecutive integers. Is the sum of all the integers in set A even?
(1) If -5 is added to set A, the set would become symmetric about 0
(2) If the largest integer of set A is removed, the sum of the remaining integers is even
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Aarav Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let the smallest integer be in set A be a. So, the other integers in set A will be a+1, a+2….a+n-1
- Sum of all integers in set
Step 3: Analyze Statement 1 independently
(1) If -5 is added to set A, the set would become symmetric about 0
- As the set becomes symmetric about 0, that would mean that there will be (upon the inclusion of -5 in set A) an equal number of terms on either side of 0 with the same magnitude (but opposite signs).
- Let’s call this new set as A’
- So, the mean of (Set A’) = 0
- So, the sum of (All the integers in set A’) = 0
- Hence, the sum of all the integers in set A is odd.
- Sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) If the largest integer of set A is removed, the sum of the remaining integers is even.
- The largest integer of Set A = a +n -1.
- So, (Sum of all the terms in set A – largest integer of set A) = even
- Let’s think of the possible ways in which difference of two integers is even:
- Case-I: even – even = even
- So, if the largest integer removed is even, the sum of all the integers in set A would be even.
- Hence
will be even - Case-II: odd – odd = even
- So, if the largest integer removed is odd, the sum of all the integers in set A would be odd.
- Hence
will be odd - As we do not have a unique answer, the statement is insufficient to answer.
- Case-I: even – even = even
Step 5: Analyze Both Statements Together (if needed)
- As we have a unique answer from step-3, this step is not required.
Answer: A
If x and y are prime integers and x < y, which of the following cannot be true?- a)x is even
- b)x + y is odd
- c)xy is even
- d)y + xy is even
- e)2x + y is even
Correct answer is option 'E'. Can you explain this answer?
If x and y are prime integers and x < y, which of the following cannot be true?
a)
x is even
b)
x + y is odd
c)
xy is even
d)
y + xy is even
e)
2x + y is even
|
|
Arjun Iyer answered |
Let's look at each answer choice:
(A) UNCERTAIN: x could be the prime number 2.
(B) UNCERTAIN: x could be the prime number 2, which when added to another prime number (odd) would yield an odd result. Ex: 2 + 3 = 5
(C) UNCERTAIN: Since x could be the prime number 2, the product xy could be even.
(D) UNCERTAIN: y > x and they are both prime so y must be odd. If x is another odd prime number, the expression will be: (odd) + (odd)(odd), which equals an even (O + O = E).
(E) FALSE: 2x must be even and y must be odd (since it cannot be the smallest prime number 2, which is also the only even prime). The result is even + odd, which must be odd.
(B) UNCERTAIN: x could be the prime number 2, which when added to another prime number (odd) would yield an odd result. Ex: 2 + 3 = 5
(C) UNCERTAIN: Since x could be the prime number 2, the product xy could be even.
(D) UNCERTAIN: y > x and they are both prime so y must be odd. If x is another odd prime number, the expression will be: (odd) + (odd)(odd), which equals an even (O + O = E).
(E) FALSE: 2x must be even and y must be odd (since it cannot be the smallest prime number 2, which is also the only even prime). The result is even + odd, which must be odd.
The correct answer is E
If z is an integer greater than 1, is z even?(1) 2z is not a factor of 8(2) 3z/4 is a factor of 6- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If z is an integer greater than 1, is z even?
(1) 2z is not a factor of 8
(2) 3z/4 is a factor of 6
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Janani Sharma answered |
Statement (1): 2z is not a factor of 8
This statement tells us that 2z does not divide evenly into 8. In other words, if we divide 8 by 2z, we will have a remainder.
To determine whether z is even or odd, we need to consider the possible values of z. If z is odd, then 2z will also be odd, and we would not be able to divide 8 by 2z without a remainder. However, if z is even, then 2z will also be even, and 8 will be divisible by 2z without a remainder.
Therefore, if 2z is not a factor of 8, it implies that z is odd, because if z were even, 2z would be a factor of 8.
Statement (2): 3z/4 is a factor of 6
This statement tells us that 3z/4 is a factor of 6. In other words, 6 is divisible by 3z/4 without a remainder.
To determine whether z is even or odd, we need to consider the possible values of z. If z is odd, then 3z/4 will also be odd, and 6 would not be divisible by 3z/4 without a remainder. However, if z is even, then 3z/4 will also be even, and 6 will be divisible by 3z/4 without a remainder.
Therefore, if 3z/4 is a factor of 6, it implies that z is even, because if z were odd, 3z/4 would not be a factor of 6.
Combined statements:
From statement (1), we know that if 2z is not a factor of 8, z must be odd.
From statement (2), we know that if 3z/4 is a factor of 6, z must be even.
Since the two statements provide contradictory information about the parity of z, we cannot determine whether z is even or odd. Therefore, neither statement alone is sufficient to answer the question.
Therefore, the correct answer is option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
This statement tells us that 2z does not divide evenly into 8. In other words, if we divide 8 by 2z, we will have a remainder.
To determine whether z is even or odd, we need to consider the possible values of z. If z is odd, then 2z will also be odd, and we would not be able to divide 8 by 2z without a remainder. However, if z is even, then 2z will also be even, and 8 will be divisible by 2z without a remainder.
Therefore, if 2z is not a factor of 8, it implies that z is odd, because if z were even, 2z would be a factor of 8.
Statement (2): 3z/4 is a factor of 6
This statement tells us that 3z/4 is a factor of 6. In other words, 6 is divisible by 3z/4 without a remainder.
To determine whether z is even or odd, we need to consider the possible values of z. If z is odd, then 3z/4 will also be odd, and 6 would not be divisible by 3z/4 without a remainder. However, if z is even, then 3z/4 will also be even, and 6 will be divisible by 3z/4 without a remainder.
Therefore, if 3z/4 is a factor of 6, it implies that z is even, because if z were odd, 3z/4 would not be a factor of 6.
Combined statements:
From statement (1), we know that if 2z is not a factor of 8, z must be odd.
From statement (2), we know that if 3z/4 is a factor of 6, z must be even.
Since the two statements provide contradictory information about the parity of z, we cannot determine whether z is even or odd. Therefore, neither statement alone is sufficient to answer the question.
Therefore, the correct answer is option B: Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
There are N students in a class. When the students are distributed into groups that contain 4A number of students each, 3 students are left without a group. When the students are distributed into groups that contain A/3 number of students each, no students are left without a group. Which of the following statements is correct?I. If the students are distributed into groups that contain A+ 1 students each, the number of students that are left without a group can be 2II. If the students are distributed into groups that contain 3 students each, no students are left without a groupIII. If the students are distributed into groups that contain 12 students each, 9 students are left without a group- a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'B'. Can you explain this answer?
There are N students in a class. When the students are distributed into groups that contain 4A number of students each, 3 students are left without a group. When the students are distributed into groups that contain A/3 number of students each, no students are left without a group. Which of the following statements is correct?
I. If the students are distributed into groups that contain A+ 1 students each, the number of students that are left without a group can be 2
II. If the students are distributed into groups that contain 3 students each, no students are left without a group
III. If the students are distributed into groups that contain 12 students each, 9 students are left without a group
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only
|
|
Janani Sharma answered |
To solve this problem, we need to use algebraic equations to represent the given information and then analyze the resulting equations.
Let's start by assigning variables to the unknowns in the problem:
N: Total number of students in the class
A: Number of students in each group
We are given two conditions:
1. When the students are distributed into groups that contain 4A number of students each, 3 students are left without a group.
This can be represented by the equation N = X * (4A) + 3, where X is the number of groups.
2. When the students are distributed into groups that contain A/3 number of students each, no students are left without a group.
This can be represented by the equation N = Y * (A/3), where Y is the number of groups.
Now, let's analyze these equations and find the values of X and Y:
1. Distributing into groups of 4A students:
N = X * (4A) + 3
N = 4AX + 3
2. Distributing into groups of A/3 students:
N = Y * (A/3)
N = (AY)/3
Now, we can equate these two equations and solve for Y:
4AX + 3 = (AY)/3
12AX + 9 = AY
12X + 9/A = Y
From this equation, we can see that Y is an integer if A is a multiple of 3. This satisfies the condition mentioned in the problem that when distributed into groups of A/3 students, no students are left without a group.
Therefore, the correct statement is:
II. If the students are distributed into groups that contain 3 students each, no students are left without a group.
Hence, the correct answer is option 'B'.
Let's start by assigning variables to the unknowns in the problem:
N: Total number of students in the class
A: Number of students in each group
We are given two conditions:
1. When the students are distributed into groups that contain 4A number of students each, 3 students are left without a group.
This can be represented by the equation N = X * (4A) + 3, where X is the number of groups.
2. When the students are distributed into groups that contain A/3 number of students each, no students are left without a group.
This can be represented by the equation N = Y * (A/3), where Y is the number of groups.
Now, let's analyze these equations and find the values of X and Y:
1. Distributing into groups of 4A students:
N = X * (4A) + 3
N = 4AX + 3
2. Distributing into groups of A/3 students:
N = Y * (A/3)
N = (AY)/3
Now, we can equate these two equations and solve for Y:
4AX + 3 = (AY)/3
12AX + 9 = AY
12X + 9/A = Y
From this equation, we can see that Y is an integer if A is a multiple of 3. This satisfies the condition mentioned in the problem that when distributed into groups of A/3 students, no students are left without a group.
Therefore, the correct statement is:
II. If the students are distributed into groups that contain 3 students each, no students are left without a group.
Hence, the correct answer is option 'B'.
Each digit in the two-digit number G is halved to form a new two-digit number H. Which of the following
could be the sum of G and H?- a)153
- b)150
- c)137
- d)128
- e)89
Correct answer is option 'D'. Can you explain this answer?
Each digit in the two-digit number G is halved to form a new two-digit number H. Which of the following
could be the sum of G and H?
could be the sum of G and H?
a)
153
b)
150
c)
137
d)
128
e)
89
|
|
Maya Choudhury answered |
Analysis:
Given Information:
- Let the two-digit number be G.
- Each digit in G is halved to form a new two-digit number H.
Approach:
- Let the tens digit of G be represented as 'a' and the units digit of G be represented as 'b'.
- The number G can be expressed as 10a + b.
- The number H can be expressed as 10(a/2) + b/2 = 5a + b/2.
Solution:
Possible Values of G and H:
- If we take G = 64, then H = 32.
- Sum of G and H = 64 + 32 = 96.
- If we take G = 58, then H = 29.
- Sum of G and H = 58 + 29 = 87.
Checking the Options:
- Option a) 153: Not possible as G will be greater than 99.
- Option b) 150: Not possible as G will be greater than 99.
- Option c) 137: Not possible as G will be greater than 99.
- Option d) 128: Possible as G = 56, H = 28.
- Sum of G and H = 56 + 28 = 84.
- Option e) 89: Not possible as G will be greater than 99.
Therefore, option d) 128 could be the sum of G and H.
If a, b, c, d, and e are integers and the expression (ab2c2 /d2e) gives a positive even integer, which of the following options must be true?I. abc is even II. a/e is positive III. a/d2 is positive - a)I only
- b)II only
- c)I and II
- d)II and III
- e)I, II, and III
Correct answer is 'C'. Can you explain this answer?
If a, b, c, d, and e are integers and the expression (ab2c2 /d2e) gives a positive even integer, which of the following options must be true?
I. abc is even
II. a/e is positive
III. a/d2 is positive
a)
I only
b)
II only
c)
I and II
d)
II and III
e)
I, II, and III
|
|
Kirti Roy answered |
If the expression (ab^2c^2 / d^2e) gives a positive even integer, we can analyze the factors in the expression to determine which options must be true.
I. abc is even:
- For the expression (ab^2c^2 / d^2e) to be even, there must be at least one 2 in the numerator (ab^2c^2) or denominator (d^2e). This means that either a, b, or c must be even.
- If a, b, or c is even, then abc will be even. Therefore, option I must be true.
II. a/e is positive:
- To determine whether a/e is positive, we need to consider the signs of a and e.
- Since the expression (ab^2c^2 / d^2e) gives a positive even integer, both the numerator and denominator must have the same sign (either both positive or both negative).
- If both a and e have the same sign, then a/e will be positive. Therefore, option II must be true.
III. a/d^2 is positive:
- Similar to the analysis for option II, we need to consider the signs of a and d.
- Since the expression (ab^2c^2 / d^2e) gives a positive even integer, both the numerator and denominator must have the same sign.
- If both a and d have the same sign, then a/d^2 will be positive. Therefore, option III must be true.
Therefore, options I and II must be true, and option III must also be true. Hence, the correct answer is option C (I and II).
I. abc is even:
- For the expression (ab^2c^2 / d^2e) to be even, there must be at least one 2 in the numerator (ab^2c^2) or denominator (d^2e). This means that either a, b, or c must be even.
- If a, b, or c is even, then abc will be even. Therefore, option I must be true.
II. a/e is positive:
- To determine whether a/e is positive, we need to consider the signs of a and e.
- Since the expression (ab^2c^2 / d^2e) gives a positive even integer, both the numerator and denominator must have the same sign (either both positive or both negative).
- If both a and e have the same sign, then a/e will be positive. Therefore, option II must be true.
III. a/d^2 is positive:
- Similar to the analysis for option II, we need to consider the signs of a and d.
- Since the expression (ab^2c^2 / d^2e) gives a positive even integer, both the numerator and denominator must have the same sign.
- If both a and d have the same sign, then a/d^2 will be positive. Therefore, option III must be true.
Therefore, options I and II must be true, and option III must also be true. Hence, the correct answer is option C (I and II).
If x and y are integers, is y even? (1) (x + 2) * (y2 + 7) is even (2) (x3 + 8) * (y2 -4) is even - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
If x and y are integers, is y even?
(1) (x + 2) * (y2 + 7) is even
(2) (x3 + 8) * (y2 -4) is even
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Aarav Sharma answered |
Step 1 and 2: Understand the question and draw inferences
We are given that x and y are integers, and we are asked if y is even. Since we do not have any more information to draw inferences from, let’s move straight to Statement 1.
Step 3: Analyze Statement 1
(x + 2) * (y2 + 7) is even
The product of two numbers is even if at least one of the two numbers is even.
Thus, three possibilities arise:
Statement 1 holds true for each of these 3 cases. Thus, we cannot ascertain for sure if y is odd or even.
Therefore, Statement 1 alone is not sufficient to answer the question.
Step 4: Analyze Statement 2
(x3 + 8) * (y2 -4) is even
Again, the product of two numbers is even if at least one of the two numbers is even.
So, three possibilities arise for this statement as well:
Statement 2 holds true for each of these 3 cases. Thus, we cannot ascertain for sure if y is odd or even.
Therefore, Statement 2 alone is not sufficient to answer the question.
Step 5: Analyze both statements together (if needed)
We have seen that
Statement 1 holds true if:
i) x is even, y is even or odd
ii) x is odd, y is odd
Statement 2 holds true if:
i) x is even, y is even or odd
ii) x is odd, y is even
Both Statements will be true at the same time only if:
x is even, y is even or odd.
Thus, even after combining both the statements, we have not been able to ascertain the even-odd nature of y.
Thus, both the statements together are not sufficient to answer the question.
Correct Answer Choice: Option E
If P and Q are positive integers, then is (P+2)(Q-1) an even number?(1) p/3Q is an even integer (2) 
is a positive odd integer- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
If P and Q are positive integers, then is (P+2)(Q-1) an even number?
(1) p/3Q is an even integer
(2) is a positive odd integer
is a positive odd integera)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Divey Sethi answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: Integers P, Q > 0
To find: Is (P+2)(Q-1) even?
- The answer is YES if
- At least one out of P + 2 and Q – 1 is even
- P + 2 is even if P is even
- Q – 1 is even if Q is odd
- At least one out of P + 2 and Q – 1 is even
- So, the answer is YES if
- Either P is Even
- Or Q is odd, or both
Step 3: Analyze Statement 1 independently
- P/3Q is an even integer.
- This means, P = (3Q)(2n) where n is a positive integer
- So, P is an even number
- Therefore, the answer is YES
Thus, Statement 1 is sufficient to answer the question
Step 4: Analyze Statement 2 independently
is an odd integer
- So, we can write: Q= (
) (2m+1), where m is an integer - Since Q and 2m + 1 are both integers,( must be an integer as well
- Since Q and 2m + 1 are both integers,(
- Therefore,√P is an integer
- Implies, that P is a perfect square
- √P has the same even-odd nature as P
- Case 1: P is even
- We’ve already determined in Steps 1 and 2 that if P is even, the answer to the question is YES
- Case 2: P is odd
- Q = (Odd - Odd)(Odd)
- Q = Even * Odd
- Q = Even
- Thus, Statement 2 doesn’t lead us to a unique answer to the question.
Therefore, Statement 2 is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3, this step is not required
Answer: Option A
Which one of the following is even?- a)3 x 4
- b)5 x 7
- c)1 x 3
- d)9 x 5
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is even?
a)
3 x 4
b)
5 x 7
c)
1 x 3
d)
9 x 5
|
|
Niti Choudhury answered |
Step 1:
5 × 7 = 35
1 × 3 = 3
9 × 5 = 45
1 × 3 = 3
9 × 5 = 45
Step 2:
Only 3 × 4 = 12 is even. Rest are odd.
Only 3 × 4 = 12 is even. Rest are odd.
Which one of the following is odd?- a)8 × 4
- b)6 × 7
- c)11 x 3
- d) 9 × 6
Correct answer is option 'C'. Can you explain this answer?
Which one of the following is odd?
a)
8 × 4
b)
6 × 7
c)
11 x 3
d)
9 × 6
|
|
Tanishq Yadav answered |
Understanding the Options
To determine which option is odd, we need to evaluate each multiplication expression to see if the result is odd or even.
Option A: 8 × 4
- Calculation: 8 × 4 = 32
- Nature: Even (as it ends in 2)
Option B: 6 × 7
- Calculation: 6 × 7 = 42
- Nature: Even (as it ends in 2)
Option C: 11 × 3
- Calculation: 11 × 3 = 33
- Nature: Odd (as it ends in 3)
Option D: 9 × 6
- Calculation: 9 × 6 = 54
- Nature: Even (as it ends in 4)
Identifying the Odd One Out
From the calculations above, we can summarize the nature of each product:
- Option A: Even
- Option B: Even
- Option C: Odd
- Option D: Even
Conclusion
The only multiplication that results in an odd number is option C (11 × 3 = 33). All other options yield even numbers. Therefore, option C is indeed the odd one out among the choices provided.
To determine which option is odd, we need to evaluate each multiplication expression to see if the result is odd or even.
Option A: 8 × 4
- Calculation: 8 × 4 = 32
- Nature: Even (as it ends in 2)
Option B: 6 × 7
- Calculation: 6 × 7 = 42
- Nature: Even (as it ends in 2)
Option C: 11 × 3
- Calculation: 11 × 3 = 33
- Nature: Odd (as it ends in 3)
Option D: 9 × 6
- Calculation: 9 × 6 = 54
- Nature: Even (as it ends in 4)
Identifying the Odd One Out
From the calculations above, we can summarize the nature of each product:
- Option A: Even
- Option B: Even
- Option C: Odd
- Option D: Even
Conclusion
The only multiplication that results in an odd number is option C (11 × 3 = 33). All other options yield even numbers. Therefore, option C is indeed the odd one out among the choices provided.
If a is an even integer and b is an odd integer, which of the following cannot be an even integer?- a)ab
- b)a/b
- c)b/a
- d)ab
- e)a2b+1
Correct answer is option 'C'. Can you explain this answer?
If a is an even integer and b is an odd integer, which of the following cannot be an even integer?
a)
ab
b)
a/b
c)
b/a
d)
ab
e)
a2b+1
|
|
Geetika Sarkar answered |
Let's look at each answer choice:
(A) EVEN: Since a is even, the product ab will always be even. Ex: 2 × 7 = 14.
(A) EVEN: Since a is even, the product ab will always be even. Ex: 2 × 7 = 14.
(B) UNCERTAIN: An even number divided by an odd number might be even if the the prime factors that make up the odd number are also in the prime box of the even number. Ex: 6/3 =2.
(C) NOT EVEN: An odd number is never divisible by an even number. By definition, an odd number is not divisible by 2 and an even number is. The quotient of an odd number divided by an even number will not be an integer, let alone an even integer. Ex: 15/4 = 3.75
(D) EVEN: An even number raised to any integer power will always be even. Ex: 21 = 2
(E) EVEN: An even number raised to any integer power will always be even. Ex: 23 = 8
The correct answer is C.
Is 'a' positive?
Statement 1: a - b > 0
Statement 2: 2a - b > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Is 'a' positive?
Statement 1: a - b > 0
Statement 2: 2a - b > 0
Statement 1: a - b > 0
Statement 2: 2a - b > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Nandita Yadav answered |
Understanding the Statements
To determine whether "a" is positive, we analyze both statements individually and together.
Statement 1: a - b > 0
- This implies that a > b.
- However, it does not provide any information about the value of "b." For example:
- If b = 1, then a could be any value greater than 1 (e.g., 2, 3).
- If b = -1, then a could be any value greater than -1 (e.g., 0, 1).
- Therefore, we cannot conclude whether "a" is positive based solely on this statement.
Statement 2: 2a - b > 0
- This implies that 2a > b, which can be rewritten as a > b/2.
- Similar to Statement 1, this does not provide enough information about "b":
- If b = 4, then a must be greater than 2 (a > 2).
- If b = -4, then a must be greater than -2 (a > -2).
- Again, we cannot determine if "a" is positive from this statement alone.
Combining Statements 1 and 2
- From both statements, we have:
- From Statement 1: a > b
- From Statement 2: a > b/2
- However, without knowing the specific values of "b," we cannot derive a definitive conclusion about "a."
- For example, if b is negative, both statements can hold true while "a" could still be negative.
Conclusion
- Since neither statement alone, nor both statements together, provide sufficient information to definitively determine if "a" is positive, the correct answer is option 'E': Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
To determine whether "a" is positive, we analyze both statements individually and together.
Statement 1: a - b > 0
- This implies that a > b.
- However, it does not provide any information about the value of "b." For example:
- If b = 1, then a could be any value greater than 1 (e.g., 2, 3).
- If b = -1, then a could be any value greater than -1 (e.g., 0, 1).
- Therefore, we cannot conclude whether "a" is positive based solely on this statement.
Statement 2: 2a - b > 0
- This implies that 2a > b, which can be rewritten as a > b/2.
- Similar to Statement 1, this does not provide enough information about "b":
- If b = 4, then a must be greater than 2 (a > 2).
- If b = -4, then a must be greater than -2 (a > -2).
- Again, we cannot determine if "a" is positive from this statement alone.
Combining Statements 1 and 2
- From both statements, we have:
- From Statement 1: a > b
- From Statement 2: a > b/2
- However, without knowing the specific values of "b," we cannot derive a definitive conclusion about "a."
- For example, if b is negative, both statements can hold true while "a" could still be negative.
Conclusion
- Since neither statement alone, nor both statements together, provide sufficient information to definitively determine if "a" is positive, the correct answer is option 'E': Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
If x and y are integers, is xy even?1) x = y + 12) x/y is an even integer
a)Exactly one of the statements can answer the questionb)Both statements are required to answer the questionc)Each statement can answer the question individuallyd)More information is required as the information provided is insufficient to answer the questionCorrect answer is option 'C'. Can you explain this answer?
2) x/y is an even integer
a)Exactly one of the statements can answer the question
b)Both statements are required to answer the question
c)Each statement can answer the question individually
d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'C'. Can you explain this answer?
|
|
Nandita Chauhan answered |
If either x or y is zero, then xy=0=even, because zero is an even integer. Zero is nether positive nor negative, but zero is definitely an even number.
An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without a remainder and as zero is evenly divisible by 2 then it must be even (in fact zero is divisible by every integer except zero itself).
An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without a remainder and as zero is evenly divisible by 2 then it must be even (in fact zero is divisible by every integer except zero itself).
If a , b, and c are integers and ab2 / c is a positive even integer, which of the following must be true?
I. ab is even
II. ab > 0
III. c is even- a)I only
- b)II only
- c)I and II
- d)I and III
- e)I, II, and III
Correct answer is option 'A'. Can you explain this answer?
If a , b, and c are integers and ab2 / c is a positive even integer, which of the following must be true?
I. ab is even
II. ab > 0
III. c is even
I. ab is even
II. ab > 0
III. c is even
a)
I only
b)
II only
c)
I and II
d)
I and III
e)
I, II, and III
|
|
Arjun Iyer answered |
If ab2 were odd, the quotient would never be divisible by 2, regardless of what c is. To prove this try to divide an odd number by any integer to come up with an even number; you can't. If ab2 is even, either a is even or b is even.
(I) TRUE: Since a or b is even, the product ab must be even
(II) NOT NECESSARILY: For the quotient to be positive, a and c must have the same sign since b2 is definitely positive. We know nothing about the sign of b. The product of ab could be negative or positive.
(III) NOT NECESSARILY: For the quotient to be even, ab2 must be even but c could be even or odd. An even number divided by an odd number could be even (ex: 18/3), as could an even number divided by an even number (ex: 16/4).
The correct answer is A.
(I) TRUE: Since a or b is even, the product ab must be even
(II) NOT NECESSARILY: For the quotient to be positive, a and c must have the same sign since b2 is definitely positive. We know nothing about the sign of b. The product of ab could be negative or positive.
(III) NOT NECESSARILY: For the quotient to be even, ab2 must be even but c could be even or odd. An even number divided by an odd number could be even (ex: 18/3), as could an even number divided by an even number (ex: 16/4).
The correct answer is A.
If A and B are positive integers, is A – B even?1. The product of A and B is even2. A + B is odd- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
If A and B are positive integers, is A – B even?
1. The product of A and B is even
2. A + B is odd
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Janani Sharma answered |
Statement 1: The product of A and B is even.
If the product of A and B is even, it means that at least one of A or B is even.
Let's consider two scenarios:
Scenario 1: A is even and B is odd
In this case, A - B will be odd.
Scenario 2: A is odd and B is even
In this case, A - B will be odd.
Therefore, based on statement 1 alone, we cannot determine if A - B is even or odd.
Statement 2: A + B is odd
If A + B is odd, it means that either A is odd and B is even or A is even and B is odd. In both cases, A - B will always be odd.
Therefore, based on statement 2 alone, we can determine that A - B is odd.
Combining both statements:
From statement 1, we know that the product of A and B is even. This means that at least one of A or B is even.
From statement 2, we know that A + B is odd. This means that either A is odd and B is even or A is even and B is odd.
In both cases, A - B will always be odd.
Therefore, combining both statements, we can determine that A - B is odd.
Hence, statement 2 alone is sufficient to answer the question, while statement 1 alone is not sufficient.
Therefore, the correct answer is option B.
If the product of A and B is even, it means that at least one of A or B is even.
Let's consider two scenarios:
Scenario 1: A is even and B is odd
In this case, A - B will be odd.
Scenario 2: A is odd and B is even
In this case, A - B will be odd.
Therefore, based on statement 1 alone, we cannot determine if A - B is even or odd.
Statement 2: A + B is odd
If A + B is odd, it means that either A is odd and B is even or A is even and B is odd. In both cases, A - B will always be odd.
Therefore, based on statement 2 alone, we can determine that A - B is odd.
Combining both statements:
From statement 1, we know that the product of A and B is even. This means that at least one of A or B is even.
From statement 2, we know that A + B is odd. This means that either A is odd and B is even or A is even and B is odd.
In both cases, A - B will always be odd.
Therefore, combining both statements, we can determine that A - B is odd.
Hence, statement 2 alone is sufficient to answer the question, while statement 1 alone is not sufficient.
Therefore, the correct answer is option B.
If q, r, and s are consecutive even integers and q < r < s, which of the following CANNOT be the value of s2 – r2 – q2?- a)-20
- b)0
- c)8
- d)12
- e)16
Correct answer is option 'C'. Can you explain this answer?
If q, r, and s are consecutive even integers and q < r < s, which of the following CANNOT be the value of s2 – r2 – q2?
a)
-20
b)
0
c)
8
d)
12
e)
16
|
|
Kiran Chauhan answered |
Understanding Consecutive Even Integers
Let’s define the consecutive even integers:
- q = n (the first even integer)
- r = n + 2 (the second even integer)
- s = n + 4 (the third even integer)
Calculating s² - r² - q²
We can express s² - r² - q²:
- s² = (n + 4)² = n² + 8n + 16
- r² = (n + 2)² = n² + 4n + 4
- q² = n²
Now, substituting these into the expression:
s² - r² - q² = (n² + 8n + 16) - (n² + 4n + 4) - n²
This simplifies to:
- s² - r² - q² = n² + 8n + 16 - n² - 4n - 4 - n²
- = 4n + 12
Possible Values
The expression 4n + 12 can take various values based on the integer n. It is essential to note that:
- Since n is an even integer, 4n is also even.
- Thus, 4n + 12 is even.
Evaluating the Options
Now we evaluate the options provided:
- a) -20 (even)
- b) 0 (even)
- c) 8 (even)
- d) 12 (even)
- e) 16 (even)
Among these, all are even numbers. However, we need to check which cannot be expressed as 4n + 12.
Finding n for each option
1. For -20: 4n + 12 = -20
- 4n = -32 => n = -8 (valid)
2. For 0: 4n + 12 = 0
- 4n = -12 => n = -3 (not valid, as n must be even)
3. For 8: 4n + 12 = 8
- 4n = -4 => n = -1 (not valid)
4. For 12: 4n + 12 = 12
- 4n = 0 => n = 0 (valid)
5. For 16: 4n + 12 = 16
- 4n = 4 => n = 1 (not valid)
Conclusion
Since n must always be an even integer, the value that cannot be achieved is option C) 8, as it yields an invalid n.
Let’s define the consecutive even integers:
- q = n (the first even integer)
- r = n + 2 (the second even integer)
- s = n + 4 (the third even integer)
Calculating s² - r² - q²
We can express s² - r² - q²:
- s² = (n + 4)² = n² + 8n + 16
- r² = (n + 2)² = n² + 4n + 4
- q² = n²
Now, substituting these into the expression:
s² - r² - q² = (n² + 8n + 16) - (n² + 4n + 4) - n²
This simplifies to:
- s² - r² - q² = n² + 8n + 16 - n² - 4n - 4 - n²
- = 4n + 12
Possible Values
The expression 4n + 12 can take various values based on the integer n. It is essential to note that:
- Since n is an even integer, 4n is also even.
- Thus, 4n + 12 is even.
Evaluating the Options
Now we evaluate the options provided:
- a) -20 (even)
- b) 0 (even)
- c) 8 (even)
- d) 12 (even)
- e) 16 (even)
Among these, all are even numbers. However, we need to check which cannot be expressed as 4n + 12.
Finding n for each option
1. For -20: 4n + 12 = -20
- 4n = -32 => n = -8 (valid)
2. For 0: 4n + 12 = 0
- 4n = -12 => n = -3 (not valid, as n must be even)
3. For 8: 4n + 12 = 8
- 4n = -4 => n = -1 (not valid)
4. For 12: 4n + 12 = 12
- 4n = 0 => n = 0 (valid)
5. For 16: 4n + 12 = 16
- 4n = 4 => n = 1 (not valid)
Conclusion
Since n must always be an even integer, the value that cannot be achieved is option C) 8, as it yields an invalid n.
If n is an integer, then which of the following statements is/are FALSE?I. n3 – n is always even.II. 8n3 +12n2 +6n +1 is always even.III. √ (4n2 – 4n +1) is always odd.- a)I only
- b)II only
- c)I and II only
- d)II and III only
- e)I, II and III
Correct answer is option 'B'. Can you explain this answer?
If n is an integer, then which of the following statements is/are FALSE?
I. n3 – n is always even.
II. 8n3 +12n2 +6n +1 is always even.
III. √ (4n2 – 4n +1) is always odd.
a)
I only
b)
II only
c)
I and II only
d)
II and III only
e)
I, II and III
|
|
Limansha Safreen answered |
√4n2-4n+1=√(2n-1)2=2n-1 for every value of n the expression becomes odd n3-n =n(n²-1)=n*(n-1)*(n+1) is always even for every n value
Is the two digit positive integer P a prime number?Statement 1: (P + 2) and (P - 2) are prime.
Statement 2: (P - 4) and (P + 4) are prime.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Is the two digit positive integer P a prime number?
Statement 1: (P + 2) and (P - 2) are prime.
Statement 2: (P - 4) and (P + 4) are prime.
Statement 2: (P - 4) and (P + 4) are prime.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Dipanjan Mehra answered |
Statement Analysis:
Statement 1:
- (P + 2) and (P - 2) are prime numbers.
- This means that P is not divisible by 2 or 3 (since P + 2 and P - 2 are prime, they cannot be divisible by 2 or 3).
- Therefore, P does not have any factors other than 1 and itself, making it a prime number.
Statement 2:
- (P - 4) and (P + 4) are prime numbers.
- Similar to Statement 1, this implies that P is not divisible by 2 or 3.
- Again, P has no factors other than 1 and itself, indicating that it is a prime number.
Combining Statements:
- Both statements independently prove that P is a prime number.
- Each statement alone is sufficient to conclude that P is a prime number.
- Therefore, the correct answer is option 'D' as each statement alone is sufficient to answer the question.
Statement 1:
- (P + 2) and (P - 2) are prime numbers.
- This means that P is not divisible by 2 or 3 (since P + 2 and P - 2 are prime, they cannot be divisible by 2 or 3).
- Therefore, P does not have any factors other than 1 and itself, making it a prime number.
Statement 2:
- (P - 4) and (P + 4) are prime numbers.
- Similar to Statement 1, this implies that P is not divisible by 2 or 3.
- Again, P has no factors other than 1 and itself, indicating that it is a prime number.
Combining Statements:
- Both statements independently prove that P is a prime number.
- Each statement alone is sufficient to conclude that P is a prime number.
- Therefore, the correct answer is option 'D' as each statement alone is sufficient to answer the question.
If r and s are positive integers, and r2 + r/s is an odd integer, which of the following cannot be even?- a)3r + 2s
- b)(r-1)(s+2)
- c)rs+1 + sr
- d)r3 +3
- e)s4 +4
Correct answer is option 'D'. Can you explain this answer?
If r and s are positive integers, and r2 + r/s is an odd integer, which of the following cannot be even?
a)
3r + 2s
b)
(r-1)(s+2)
c)
rs+1 + sr
d)
r3 +3
e)
s4 +4
|
|
Manasa Gupta answered |
Step 1: Question statement and Inferences
Given: r and s are positive integers
r2 + r/s is odd
To Infer: Let’s try to infer whether r and s are even or odd.
Let’s first consider the possibility that r is odd.
Case (i): r is odd
--> r2 is odd (Odd × Odd = Odd)
Now, r2 + r/s = Odd
--> Odd + r/s = Odd
--> r/s = Even (Odd -Odd = Even)
--> Odd/s = Even
--> s × Even = Odd
Not possible! When one of the numbers being multiplied is even, the product is always even
Conclusion: r cannot be odd
--> r must be even
Let’s also see if we can determine whether s is even or odd.
We know now that r is even
--> r2 is even (Odd × Odd = Odd)
Now, r2 + r/s = Odd
--> Even + r/s = Odd
--> r/s = Odd (Odd -Even = Odd)
--> Even/s = Odd
--> s × Odd = Even
--> s is Even
Conclusion: Both r and s are even integers
Step 2: Analyzing the given options
- 3r + 2s
Both r and s are even
--> 3r is even (Odd × Even = Even)
2s is even (Even × Even = Even)
--> 3r + 2s is even (Even + Even = Even)
- (r-1)(s+2)
Both r and s are even
--> r-1 is odd (Even -Odd = Odd)
s + 2 is even (Even + Even = Even)
--> (r-1)(s+2) is even (Odd × Even = Even)
- rs+1 + sr
Both r and s are even
An even number multiplied with itself any number of times will give an even product
--> rs+1 is even
sr is even
--> rs+1 + sr is even
- r3 +3
r is even
--> r3 is even
--> r3 + 3 is odd
We don’t need to analyze Option E since we have already found the expression that cannot be even.
Step 3: Calculating the final answer
Among the given options, Option D cannot be even
Answer: Option (D)
If n is an integer, the number of integers between, but not including, n and 3n cannot beI. 13II. 14III. 15- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
If n is an integer, the number of integers between, but not including, n and 3n cannot be
I. 13
II. 14
III. 15
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above
|
|
Gitanjali Kumar answered |
To determine the number of integers between, but not including, n and 3n, we need to calculate the difference between these two values and subtract one.
Let's assume n is a positive integer greater than 1.
The difference between 3n and n can be calculated as follows:
3n - n = 2n
So, there are 2n integers between, but not including, n and 3n.
We are given three options for the number of integers between n and 3n: 13, 14, and 15. Let's analyze each option:
I. 13:
If there are 13 integers between n and 3n, then 2n = 13.
This implies that n = 13/2, which is not an integer.
Therefore, option I is not possible.
II. 14:
If there are 14 integers between n and 3n, then 2n = 14.
This implies that n = 14/2 = 7.
So, when n = 7, there will be 14 integers between n and 3n.
Therefore, option II is possible.
III. 15:
If there are 15 integers between n and 3n, then 2n = 15.
This implies that n = 15/2, which is not an integer.
Therefore, option III is not possible.
From the analysis above, we can conclude that the number of integers between, but not including, n and 3n cannot be 13 or 15. However, we have found that it can be 14.
Therefore, the correct answer is option II only (b).
Let's assume n is a positive integer greater than 1.
The difference between 3n and n can be calculated as follows:
3n - n = 2n
So, there are 2n integers between, but not including, n and 3n.
We are given three options for the number of integers between n and 3n: 13, 14, and 15. Let's analyze each option:
I. 13:
If there are 13 integers between n and 3n, then 2n = 13.
This implies that n = 13/2, which is not an integer.
Therefore, option I is not possible.
II. 14:
If there are 14 integers between n and 3n, then 2n = 14.
This implies that n = 14/2 = 7.
So, when n = 7, there will be 14 integers between n and 3n.
Therefore, option II is possible.
III. 15:
If there are 15 integers between n and 3n, then 2n = 15.
This implies that n = 15/2, which is not an integer.
Therefore, option III is not possible.
From the analysis above, we can conclude that the number of integers between, but not including, n and 3n cannot be 13 or 15. However, we have found that it can be 14.
Therefore, the correct answer is option II only (b).
For non-negative integers x, y, and z, is xz odd?
1) xz = odd
2) x = 2y
- a)Exactly one of the statements can answer the question
- b)Both statements are required to answer the question
- c) Each statement can answer the question individually
- d)More information is required as the information provided is insufficient to answer the question
Correct answer is option 'A'. Can you explain this answer?
For non-negative integers x, y, and z, is xz odd?
1) xz = odd
2) x = 2y
a)
Exactly one of the statements can answer the question
b)
Both statements are required to answer the question
c)
Each statement can answer the question individually
d)
More information is required as the information provided is insufficient to answer the question
|
|
Athira Choudhury answered |
(1) The product xz is odd.
=> x, z are odd => xz odd => SUF
=> x, z are odd => xz odd => SUF
(2) x = 2y
=> x is even => xz even => SUF
Chapter doubts & questions for Even, Odd, Positive and Negative Numbers - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Even, Odd, Positive and Negative Numbers - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
191 videos|289 docs|197 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup