Explore Exams
Login Signup
Sign in Open App
All Exams  >   GMAT  >   35 Days Preparation for GMAT  >   All Questions

All questions of Sets for GMAT Exam

Of the 150 people in a party, 70 were women. 30 women preferred Drink A. 50 people didn’t prefer Drink A. What was the total number of men who preferred drink A?     
  • a)
    40
  • b)
    50
  • c)
    60
  • d)
    70
  • e)
    80
Correct answer is option 'D'. Can you explain this answer?

Anaya Patel answered
As there are multiple information within the question, we need to think of a way in which we can efficiently organize this information.
We can either use a Tree structure or a Venn Diagram to solve this question.
 Method 1: Tree Structure
The best way here is to use a Tree structure to organize this given information.
 Let’s draw our Tree structure with the given information.
  • Total number of people = 150
  • Number of women = 70
  • Number of women who preferred Drink A = 30
  • Number of people who didn’t prefer Drink A = 50
Drawing the tree structure, we get
Now that we have organised information in a Tree Structure, we can easily see that
  • No: of men who didn’t prefer Drink A =
  • No: of people who didn’t prefer Drink A (given) –  No: of women who didn’t prefer Drink A (from tree structure)
 
  • No: of men who didn’t prefer Drink A =  50 – 40 = 10
Therefore,
Out of the 80 men, 10 men didn’t prefer Drink A.
Hence,
  • Number of men who preferred Drink A = Total number of men - Number of men who didnt prefer Drink A
  • Number of men who preferred Drink A = 80 – 10 = 70
 Correct Answer: Option D
 
Method 2: Venn Diagram
We have seen that Tree Structure provides a easy way to solve this question.
We can also use a Venn Diagram to solve this question, although this requires a bit of advanced thinking with regards to appropriate selection of sets.
We are given that there are 150 people in a party of which 70 are women and 80 are men. We are given information about the preferences of these people of a drink A.
  • 30 out of 70 women prefer drink A.
  • This means, 40 women don’t prefer drink A.
  • Now, we have to find the number of men who prefer drink A. 
    Let us consider two sets: Women and Drink A.
    Therefore, our Venn Diagram will look like this:
In this diagram,
  • X = Number of men who prefer drink A. This is the number we need to find.
  • Y = Number of men who don’t prefer drink A
Now, the sum of the number of people in all the four zones will be equal to the total number of guests at the party.
Thus,
  • 40 + 30 + X + Y = 150
That is,
  • X + Y = 80 . . . (1)
(Basically, Equation 1 only conveys that the number of men at the party was 80)  
Finding required values
We are also given that the number of people who didn’t prefer drink A is 50.
This means,
The number of people who fall outside of the gray circle (The ‘Prefer A’ circle) is 50
Thus,
  • 40 + Y = 50
  • Y = 10 . . . (2)
Calculating the final answer
Substituting the value of Y in Equation (1) we get:
  • X = 70
Thus, the number of men who prefer drink A is 70   
Correct Answer: Option D
Clear all your doubts with EduRev

Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Then the number of subsets of A containing exactly two elements is
  • a)
    45
  • b)
    20
  • c)
    35
  • d)
    40
  • e)
    90
Correct answer is option 'A'. Can you explain this answer?

Naveen Basu answered
Explanation:

Counting subsets with exactly two elements:
To find the number of subsets of A containing exactly two elements, we need to choose 2 elements out of the 10 elements in set A. This can be done using combination formula C(n, r) = n! / [r! * (n-r)!].

Calculating the number of subsets:
C(10, 2) = 10! / [2! * 8!] = 45.
Therefore, the number of subsets of A containing exactly two elements is 45.
So, the correct answer is option 'A' (45).

A class was tested on two subjects-Mathematics and Physics. 80% of the students passed in Mathematics. This number was 120 more than the number of students who passed in Physics. If 180 students passed in both the subjects and the ratio of students who passed only in Physics and only in Mathematics was 1:7, how many students passed in neither of the two subjects? 
  • a)
    40
  • b)
    50
  • c)
    60
  • d)
    70
  • e)
    80
Correct answer is option 'C'. Can you explain this answer?

Moumita Sen answered
Step 1: Question statement and Inferences
We are given the performance of students in a class test that consists of two subjects: Physics and Mathematics. Let’s say the total number of students who appeared for the quiz be N. So, the Venn diagram for the given information can be drawn as under:
Let
P = Number of students who passed only in Physics
M = Number of students who passed only in Mathematics
Z = Number of students who passed neither in Physics nor in Mathematics.
Let us now analyze the pieces of given information, one by one.
First, we are told that 80% of the students passed in Mathematics. The point to note here is that the statement doesn’t say ‘ONLY Mathematics’. Therefore, this percentage term includes students who passed only in Mathematics as well as students who passed in both Mathematics and Physics.
Therefore, we can write the equation:
   M+180=80 of N
Or,  M=0.8N - 180  . . . (1) 
We are also told that the number of students who passed in Mathematics was 120 more than the number of students who passed in Physics.
Again, we note that this statement doesn’t say ‘Only Mathematics’ or ‘Only Physics’. The number of students who passed in Physics will be equal to the number of students who passed only in Physics PLUS the number of students who passed in both subjects.
Thus, we can write the equation:
 M + 180 = (P+180) + 120
Or, M = P + 120  . . . (2)
Finally, we are given that
Or, M = 7P . . . (3)
 Step 2: Finding required values
Substituting the value of M from Equation 3 in Equation 2:
7P = P + 120 
6P = 120
P = 20
From Equation 2:
M = 140
From Equation 1:
140 = 0.8N – 180
 
N = 400
Step 3: Calculating the final answer
Now, P + 180 + M + Z = N
Substituting the values of P, M and Z in this equation, we get:
20 + 180 + 140 + Z = 400
340 + Z = 400
Z = 60
So, the number of students who failed in both the subjects is 60    
Answer: Option (C)

Out of the 150 students of School X, 40 students have opted for only French as an extra subject. Some students have opted for German as an extra subject and 30 students have opted neither for German nor French. What is the total number of students who have opted for only German?
(1) The total number of students opting for at least one subject out of German and French is 120. 
(2) The number of students who opted for both German and French is one-third of the number of students who opted for neither of the two subjects. 
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'B'. Can you explain this answer?

Kavya Saxena answered
Steps 1 & 2: Understand Question and Draw Inferences
We are given that there are 150 students in a school. Out of these 150 students, 40 have opted only for French as an extra subject.
There are 30 students who haven’t opted for any of German or French as the extra subject.
Let’s say:
X = Number of students who opted for both the subjects
Y = Number of students who opted only for German as the extra subject
So, the above information can be represented as follows:   
The sum of the numbers in the four zones of the Venn diagram will be equal to the total number of students.
Thus,
40 + X + Y + 30 = 150
We get: 
X + Y = 80      ……….. (1)
The question asks us to find the value of Y.
Step 3: Analyze Statement 1
The total number of students opting for at least one subject out of German and French is 120 
This means,
40 + X + Y = 120
Or, X + Y = 80
As shown in equation (1), we already have this information. However, since we don’t have the value of X, we can’t find the value of Y.
Hence, Statement 1 is not sufficient to answer the question: What is the value of Y?
Step 4: Analyze Statement 2
The number of students who opted for both German and French is one-third of the number of students who opted for neither of the two subjects  
Per this statement,
   X=1/3(30)=10
By plugging in the value of X in Equation (1), we get,
Y = 70
Hence, Statement 2 alone is sufficient to answer the question: What is the value of Y?  
Step 5: Analyze Both Statements Together (if needed)
Since Statement 2 alone is sufficient to answer the question, we don’t need to perform this step.
Answer: Option (B)  

A group of friends went to an ice-cream parlour and ordered only two types of ice-cream - chocolate and strawberry. Of the people in the group, at least one person ate only one type ice-cream, some people ate both types of ice-cream and at least one person did not eat any type of ice-cream. Did more people eat chocolate ice-cream than strawberry ice-cream?
1) The ratio of the number of people who ate chocolate ice-cream and people who ate strawberry ice-cream was greater than the ratio of the total number of people who went to ice-cream parlour and the number of people who did not eat any type of ice-cream.
2) The number of people who ate only one type of ice-cream is greater than the number of people who ate strawberry ice-cream.
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?

Gitanjali Kumar answered
Understanding the Problem
The question asks whether more people ate chocolate ice-cream than strawberry ice-cream, given certain conditions about the group of friends.
Key Information
- Some people ate both types of ice-cream.
- At least one person had only one type.
- At least one person did not eat any ice-cream.
Analysis of Statement 1
- Statement 1 provides a ratio comparison:
- The ratio of people who ate chocolate to those who ate strawberry is greater than the ratio of the total number of people to those who did not eat any ice-cream.
- Let:
- C = number of people who ate chocolate.
- S = number of people who ate strawberry.
- T = total number of people.
- N = number who didn't eat any ice-cream.
- The inequality can be expressed as: C/S > T/N.
- This implies that C/S must be a significant ratio, suggesting that there are more chocolate eaters compared to strawberry eaters, confirming that more people ate chocolate.
Analysis of Statement 2
- Statement 2 states:
- The number of people who ate only one type of ice-cream is greater than the number of people who ate strawberry.
- This does not provide sufficient information about the total counts of chocolate and strawberry eaters separately, making it impossible to conclude whether more people ate chocolate than strawberry.
Conclusion
- Statement 1 alone is sufficient to answer the question about whether more people ate chocolate than strawberry.
- Statement 2 alone is not sufficient.
Therefore, the correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.

In a college, 300 graduates sit for the recruitment drive of three companies-A, B, and C. 120 graduates are placed in A, 180 are placed in B and 80 are placed in C. 5 students are placed in all the three companies. How many of them are not placed in any of the three companies?
(1) Out of the graduates who got placed in A, 75 and 45 are also placed in B and C respectively.
(2) Out of the graduates who got placed in C, 35 are also placed in B.   
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?

Tanishq Yadav answered
Steps 1 & 2: Understand Question and Draw Inferences
We are given that 300 graduates from a college participate in recruitment process conducted by companies A, B, and C. The results of the process are as follows:  
Let’s say:
X = the number of students who got placed in A  
Y = the number of students who got placed in B  
Z = the number of students who got placed in C  
P = the number of students who got placed in B and C 
Q = the number of students who got placed in A and C 
R = the number of students who got placed in A and B 
S = the number of students who got placed in all three companies
T = the number of students who were not placed in any of the companies
Now, per the question:
X + Y + Z + P + Q + R + S + T = 300    ………… (1) 
X + P + Q + S = 80      …………. (2)
Y + P + S + R = 180   …………. (3)
Z + Q + S + R = 120   …………. (4)
S = 5               …………. (5)
We need to find the value of T. However, we have 8 variables and only 5 equations. So, we need three more equations in these variables to find the value of T.  
Step 3: Analyze Statement 1
Statement 1 says: Out of the number of graduates who got placed in A, 75 and 45 are also placed in B and C respectively.
 Per this statement,
 The number of students placed in A and B = 75
We know from the diagram that the students placed in A and B consist of R and S. So,
R + S = 75     
So,  R = 70    ………….. (6)
Note that, since S represents the number of students who were placed in all the three companies, it includes the number of students who were placed in A and B.
The number of students placed in A and C = 45
We know from the diagram that the students placed in A and B consist of Q and S. So,
Q + S = 45     
So,  Q = 40    ………….. (7)
Thus, we get a total of 7 equations, but we have 8 variables. So, we still can’t find the value of T.
 Hence, statement I alone is not sufficient to answer the question: What is the value of T?  
 Step 4: Analyze Statement 2
Statement 2 says:  Out of the number of graduates who got placed in C, 35 are also placed in B.     
 The number of students placed in B and C = 35
We know from the diagram that the students placed in B and C consist of P and S. So,
P + S = 35     
So,  P = 30    ………….. (8)
 Thus, we get a total of 6 equations (5 from Steps 1 and 2, and another one in this step, from Statement 2), but we have 8 variables. So, we still can’t find the value of T.
 Hence, statement II alone is not sufficient to answer the question: What is the value of T?  
 Step 5: Analyze Both Statements Together (if needed)
Since statement I and II alone are not sufficient to answer the question, let’s analyse both the statements together: 
 Now, the combination of both the statements gives us 8 equations in 8 variables, we can easily find the value of T. By plugging in the values of P, Q, and R, we get:
Now, by plugging in the values of P, Q, R, and S in the following equations, we get:
X + Y + Z + P + Q + R + S + T = 300    ………… (1) 
X + P + Q + S = 80      …………. (2)
Y + P + S + R = 180   …………. (3)
Z + Q + S + R = 120   …………. (4)
 
X = 5
Y = 75
Z = 5
Thus, from equation (1):
5 + 75 + 5 + 40 + 30 + 70 + 5 + T = 300
230 + T = 300
So,  T = 70
So, there are total 70 students who were not placed in any of the companies.
Both statements together are sufficient to answer the question.
Answer: Option (C)  
(Note: We have solved for the value of T only to illustrate how such an answer could be calculated if one wanted to solve for T. The given question is a Data Sufficiency question, and therefore, you as a student need not solve for the value of T. Once you determine in Step 5 that you have 8 equations and 8 variables, and therefore the two statements together are sufficiency to find a unique value of T, you can-you should! – stop there and confidently mark the answer as C)

A survey was conducted to find out the number of languages spoken by the 210 employees of a company. It was found that 60 employees did not speak English, 150 employees did not speak German and 170 employees did not speak French. If there were 20 employees who did not speak German or English and 20 employees who did not speak French or English, what was the maximum number of employees who spoke only English? Assume that each of the employees spoke at least one language and no employee spoke any language other than English, French and German.
  • a)
    110
  • b)
    120
  • c)
    130
  • d)
    140
  • e)
    150
Correct answer is option 'C'. Can you explain this answer?

Bhavana Kulkarni answered
Given
  • Number of employees = 210
  • Number of employees who did not speak English = 60
    • So, number of employees who spoke English = 210 – 60 = 150
  • Number of employees who did not speak German = 150
    • So, number of employees who spoke German = 210 – 150 = 60
  • Number of employees who did not speak French = 170
    • So, number of employees who spoke French = 210 – 170 = 40
  • Number of employees who did not speak German or English = 20
    • So, these employees must speak only French (because it’s given that each employee speaks at least one language)
  • Number of employees who did not speak French and English = 20
    • So, these employees must speak only German (because it’s given that each employee speaks at least one language)
To Find: Maximum number of employees who spoke only English
Approach
 
  1. To find the maximum number of employees who spoke only English, we will first analyse the relation between total number of employees and number of employees who speak only English.
    1. Total number of employees = number of employees (who only speak English + who only speak French + who only speak German + who speak both German & French + who speak both German & English + who speak both French & English + who speak all the three languages + who speak none of the languages)
    2. Number of employees who only speak English = (Total number of employees) – (number of employees (who only speak French + who only speak German + who speak both German & French + who speak both German & English + who speak both French & English + who speak all the three languages + who speak none of the languages)
    3. As we need to maximize the number of employees who spoke only English, we need to minimize the number of employees who spoke English as well as some other language.
    4. So, of the employees who speak more one language we would maximize the number of employees who spoke only French and German
       
  2. Now, we know the number of employees who spoke French and German and also the number of employees who spoke only  French and German.
     
  3. We will use this information to maximize the number of employees who spoke only French and German.
 
Working Out
  1. As there are 40 employees who spoke French and 20 employees who only spoke French,              
    1. Number of employees who spoke French and some other language = 40 – 20 = 20
  2. Similarly, as there are 60 employees who spoke German and 20 employees who spoke only German,
    1. Number of employees who spoke German and some other language = 60 – 20 = 40
  3. Total number of employees who spoke more than 1 language
    1. Number of employees who spoke English + Number of employees who spoke French + Number of employees who spoke German – Total number of employees = 150 + 60 + 40 – 210 = 40
  4. As there are 40 employees who spoke more than 1 language, we will try to distribute maximum number of these employees into the number of employees who spoke French and German only.
    1. As there are 20 employees who spoke French and some other language and there are 40 employees who spoke German and some other language, the maximum number of employees who spoke French and German = 20
  5. So, that still leaves us with 40 – 20 = 20 employees who spoke German and some other language.
    1. The only possibility is for these employees to speak German and English
  6. So, there are 20 employees who spoke English and some other language
  7. As there are 150 employees who spoke English, there can be a maximum of 150 – 20 = 130 employees who spoke only English.
 
Answer: C

If A = {1, 3, 5} then find the cardinality of the power set of A ?
  • a)
    2
  • b)
    8
  • c)
    9
  • d)
    6
  • e)
    Cannot be determined
Correct answer is option 'B'. Can you explain this answer?

Sameer Kumar answered
Explanation:

To find the cardinality of the power set of a set A, we need to find the number of all possible subsets of A.

The set A = {1, 3, 5} has 3 elements.

The power set of A will contain all possible subsets of A, including the empty set and the set A itself.

Empty set:
The empty set is a subset of every set, including A. Therefore, it will be included in the power set.

Single-element subsets:
For each element in A, we can have a subset containing only that element. In this case, we have 3 elements in A, so we will have 3 single-element subsets.

Two-element subsets:
For each pair of elements in A, we can have a subset containing those two elements. In this case, we have 3 elements in A, so we can choose 2 elements in C(3,2) = 3 ways. Therefore, we will have 3 two-element subsets.

Three-element subset:
The set A itself is a three-element subset.

Therefore, the power set of A will contain:
- 1 empty set
- 3 single-element subsets
- 3 two-element subsets
- 1 three-element subset

The total number of subsets in the power set is 1 + 3 + 3 + 1 = 8.

Hence, the cardinality of the power set of A is 8.

Answer:
The correct answer is option B) 8.

A survey was conducted among a group of 83 American travel enthusiasts to determine the countries that the group members had visited. The data collected in the survey is summarized as below:
  • 40 had visited Australia
  • 30 had visited Belgium
  • 20 had visited Chile
  • 8 had visited Australia and Belgium
  • 12 had visited Belgium and Chile
  • 4 had visited Australia and Chile
  • 14 had visited none of the three countries
What is the number of surveyed travel enthusiasts who had visited all the three countries?
  • a)
    0
  • b)
    1
  • c)
    2
  • d)
    3
  • e)
    4
Correct answer is option 'D'. Can you explain this answer?

Athul Joshi answered
Given:
  • Total surveyed people = 83
  • Data about their visits to 3 countries is provided: Australia (referred to as A in the solution), Belgium (B) and Chile (C)
To find: The number of surveyed people who visited all 3 countries.
Approach:
  1. Let the number of surveyed people who visited all 3 countries be x
  2. Now, since this is a question that involves 3 sets (A, B and C), the most efficient way to solve it will be Venn Diagram. So, we’ll represent the given information in a Venn Diagram. Since x is the only unknown quantity in this question, we’ll be able to get a linear equation in x and so, get a unique value of x.
 
Working Out:
 
  • Since total number of people is 83, we can write:
    • {(28+x) +(8-x) +x+(4-x)} + {(10+x) + (12-x)} + (4+x) + 14 = 83
  • So, 40 + 40 + x = 83
  • 80 + x = 83
  • Therefore, x = 3
 
Looking at the answer choices, we see that the correct answer is Option D

If A = {1, 2, 5, 7} and B = {2, 4, 6} then find the number of proper subsets of A U B ?
  • a)
    127
  • b)
    64
  • c)
    63
  • d)
    31
  • e)
    none of these
Correct answer is option 'C'. Can you explain this answer?

Nikhil Sengupta answered
Step 1: Find A U B
To find the union of sets A and B:
- A = {1, 2, 5, 7}
- B = {2, 4, 6}
The union A U B combines all unique elements from both sets:
- A U B = {1, 2, 4, 5, 6, 7}
Step 2: Count the Elements in A U B
Now, we count the number of elements in A U B:
- Number of elements in A U B = 6 (i.e., 1, 2, 4, 5, 6, 7)
Step 3: Calculate Total Subsets of A U B
The formula for the total number of subsets of a set is 2 raised to the power of the number of elements in the set:
- Total subsets = 2^n, where n is the number of elements
Thus, for A U B:
- Total subsets = 2^6 = 64
Step 4: Identify Proper Subsets
A proper subset is any subset that is not equal to the set itself. Therefore, to find the number of proper subsets, we subtract 1 from the total number of subsets:
- Proper subsets = Total subsets - 1 = 64 - 1 = 63
Conclusion
The number of proper subsets of A U B is:
- 63
Thus, the correct answer is option 'C'.

100 students appeared for two tests-Physics and Chemistry. 60 students passed the Physics test and 33 students passed the Chemistry test. The school had announced a cash prize of $1,000 for every student who passed in at least one test. What is the difference between the maximum and minimum possible values of the cash disbursal done by the school?   
  • a)
    $7000
  • b)
    $33000
  • c)
    $40000
  • d)
    $60000
  • e)
    $67000
Correct answer is option 'B'. Can you explain this answer?

Tanishq Yadav answered
Step 1: Question statement and Inferences
We are given that a total of 100 students appeared in the two tests. Out of these 100 students, 60 passed in Physics and 33 passed in Chemistry. The point to note here is that the question statement doesn’t say “60 students passed ONLY in Physics” or “33 students passed ONLY in Chemistry”. Therefore, the numbers given here are for the total number of students who passed in Physics and Chemistry respectively.
If a student passes in at least one test, the school gives him a cash prize of $1,000. We have to find the difference in the maximum and minimum possible values of the prize money that the school disbursed to the students. 
Let’s say,
P = the number of students who passed only in Physics 
C = the number of students who passed only in Chemistry
X = the number of students who passed both the tests
 
Given that, 
Number of students who passed in Physics = 60
This means, P + X = 60
Or, P = 60 – X
Similarly, C + X = 33
This means, C = 33 – X
Let the number of students who qualify for money disbursement be Z.
Thus
Z = P + C + X
That is, Z = (60 -X) + (33 – X) + X
Z = 93 -X
As we can see, the value of Z depends on the value of X.
Case 1: Maximum value of Z
Z will be maximum when the value of X is the least. The lowest possible value of X is zero (X cannot be negative because it denotes the number of students)
Thus, Zmax = 93
Case 2: Minimum value of Z
Z will be minimum when the value of X is the maximum.
Since there are only 33 students who passed in Chemistry, X cannot exceed 33. Thus, the maximum value of X can be 33.
(Logically speaking: the number of students who passed BOTH Physics and Chemistry cannot be greater than the total number of students who passed Chemistry)
Thus, Zmin = 93 – 33 = 60
Step 2: Finding required values
Maximum possible amount of disbursement by the school = 1000* Zmax  = 1000*93 = $93,000
Minimum possible amount of disbursement by the school = 1000* Zmin  = 1000*60 = $60,000
Step 3: Calculating the final answer
The difference in the maximum and the minimum possible amounts of disbursement
= $93,000 -$60,000
= $33,000  
 
Answer: Option (B)

In a survey conducted on women regarding their preference of cosmetics, it was found that 80% of the women surveyed were using at least one of the three brands-H & S, Dove and Pantene. 40% of those surveyed were using H & S, 30% of surveyed were using Dove and 60% of surveyed were using Pantene. 20% of the surveyed use all the three brands. What percentage of the women surveyed use more than one of the given three brands?
  • a)
    10
  • b)
    20
  • c)
    25
  • d)
    30
  • e)
    40
Correct answer is option 'D'. Can you explain this answer?

Tanishq Yadav answered
Step 1: Question statement and Inferences
We are given that a survey was conducted on some women regarding their preferences of cosmetics. The results of the survey are as follows:  
The percentage of women who use H&S = 40%
The percentage of women who use Pantene = 60%
The percentage of women who use Dove = 30%
Let
X = the percentage of women who use only H&S 
Y = the percentage of women who use only Pantene 
Z = the percentage of women who use only Dove 
P = the percentage of women who use H&S and Pantene 
Q = the percentage of women who use Dove and H&S 
R = the percentage of women who use Dove and Pantene 
S = the percentage of women who use all three products
 
Now, since there are only 80% women who use at least one of the three brands, there are 20% women who don’t use any of the brands.
Thus,
X + Y + Z + P + Q + R + S = 80%    ………… (1)
 Step 2: Finding required values
We can also say from the given diagram:
40% = X + P + Q + S    ………… (2)
30% = Z + Q + R + S   ………… (3) 
60% = P + R + Y + S   ………… (4) 
Adding equation (2), (3), and (4), we get:  
130% = (X + Y + Z + P + Q + R + S) + P + Q + R + 2*S
Now, the above expression in brackets is equal to 80%              [from equation (1)]
130% = 80% + P + Q + R + 2*S
50% = P + Q + R + 2*20%
P + Q + R = 10%
Step 3: Calculating the final answer
Now, the percentage of women who use more than one brands
= the percentage of women who use two brands + the percentage of women who use three brands
= (P + Q + R) + S
= 10% + 20%
= 30% 
Answer: Option (D)
(Note: In this question, a percentage term like 30% denotes 30% ‘of the total women surveyed’. Let the total number be t. Since the base of each percentage term used in the solution is the same – the total number of surveyed women-percentages have been added and subtracted without writing the base – as in, 30% of t – every time. If the base of each percentage term was not the same, it would have been imperative for us to specify % ‘of what’ with each term) 

In a certain class of 66 students, 30 students study Science, 40 students study Humanities and 40 students study Dance. If all the students studied at least one of the subjects, then what is the maximum possible number of students who study all the three subjects?
  • a)
    38
  • b)
    35
  • c)
    32
  • d)
    22
  • e)
    20
Correct answer is option 'D'. Can you explain this answer?

Let's Tute answered
Given:
  • Total number of students = 66
  • Students who take:
    • Science = 30
    • Humanities = 40
    • Dance = 40
    • None of these 3 subjects = 0
  • Maximum possible number of students who study all 3 subjects = x
 
To find: X – N = ?
Approach:
  1. To answer the question, we need to find the value of x
  2. We’ll visually represent the given information to analyze the maximum possible overlap for 3 subjects.
Working Out:
The shaded part represents the students who study all three subjects: Science, Humanities, and Dance.
In the problem, the shaded part is labeled as x, which represents the maximum number of students who study all three subjects.
  • Analyzing the Maximum possible overlap for the 3 subject
  • To maximize x, i.e. to minimize the other overlap regions, among the sets, let’s consider the number of students who study only two subjects to be 0
    • So, number of students who study only Science = 30 – x
    • Number of students who study only Humanities = 40 -x
    • Number of students who study only Dance = 40 – x
  • So, number of students who study only 1 subject + Number of students who study all the 3 subjects = 66
  • (30-x) + (40-x) + (40- x) + x = 66
  • 2x = 44
  • x = 22
  • Getting to the answer
    • So, the maximum number of students who can study all the 3 subjects is 22
Looking at the answer choices, we see that the correct answer is Option D

Of the 48 students in a class, 16 like to study History. What percentage of the girls in the class do not like to study History?
(1) One-third of the boys in the class like to study History
(2) The number of girls who like History is 50 percent of the number of girls who do not like History
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?

Imk Pathsala answered
Steps 1 & 2: Understand Question and Draw Inferences
Given:
  • Let number of girls who do not like history = X
  • Total number of girls = Y
  • We need to find the value of X/Y
  •  to answer the question
  • Completing the above table in terms of X and Y:
Step 3: Analyze Statement 1 independently
One-third of the boys in the class like to study History
Sufficient
Step 4: Analyze Statement 2 independently
The number of girls who like History is 50 percent of the number of girls who do not like History
Sufficient
 
Step 5: Analyze Both Statements Together (if needed)
Since we’ve already arrived at a unique answer in Step 3 and Step 4, this step is not required
 
Answer: Option D

Out of the 500 GMAT aspirants who registered on the e-GMAT website a single day, 50% registered for Verbal courses and 200 registered for Quant courses.  How many students registered for neither of the Verbal and Quant course?
(1) 30% of the aspirants registered only for Quant courses
(2) 10% of the aspirants registered for both Quant and Verbal courses
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. 
  • c)
    BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. 
  • d)
    EACH statement ALONE is sufficient. 
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?

Tanishq Yadav answered
Steps 1 & 2: Understand Question and Draw Inferences
We are given that 500 GMAT aspirants registered on e-GMAT website on a single day. These registrations came in three sections: Quant, Verbal, and Others. 
Let’s say:
X = the number of students who registered in only Verbal courses
Y = the number of students who registered in only Quant courses
Z = the number of students who registered in both Quant and Verbal
P = the number of students who registered for neither of the Verbal or Quant courses.
We are told that
The total number of students who registered in Verbal courses = 50% of 500 =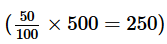
Thus, X + Z = 250          ……………… (1)
Also given:
The total number of students who registered in Quant courses = 200
Thus, Y + Z = 200          ……………… (2)
Now, the sum of the numbers in the four zones of the Venn diagram will be equal to the total number of students.
That is,
X + Y + Z + P = 500      ………. (3)
We need to find the value of P.
Since we have three equations in four unknowns, we just need one more equation in these unknowns to find the value of P.
Step 3: Analyze Statement 1
30% of the aspirants registered only for Quant courses
Per this statement,
Y = 30% of 500 = 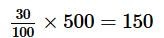 ………. (4)
Substituting Equations (1) and (4) in Equation (3):
250 + 150 +P = 500
P = 100
Hence, Statement 1 alone is sufficient to answer the question: What is the value of P?  
(Note: We have shown the actual calculation for P here just to illustrate the calculation. In the exam, once you determine that Statement 1 provides enough information for you to solve the question, you can move to Step 4)
Step 4: Analyze Statement 2
10% of the aspirants registered for both Quant and Verbal courses   
Per this statement,
Z = 10% of 500 =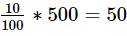 
 By substituting this value of Z in Equations 1 and 2 respectively, we’ll be able to find the values of X and Y. And by substituting the values of X, Y and Z in Equation 3, we will be able to determine the value of P.
Thus, Statement 2 alone is sufficient to find the value of P.
Step 5: Analyze Both Statements Together (if needed)
Since Statement 1 and 2 alone are sufficient to answer the question, we don’t need this step.
Answer: Option (D)  

In a certain group of women, 70 percent of the women were employed and 25 percent did not have a graduate degree. Which of the following statements cannot be true?
  1. No woman in the group who had a graduate degree was unemployed
  2. Less than half of the women in the group were employed and had a graduate degree
  3. The number of unemployed women with a graduate degree was 50 percent greater than the number of employed women without a graduate degree
  • a)
    I only
  • b)
    II only
  • c)
    III only
  • d)
    I and III only
  • e)
    II and III only
Correct answer is option 'A'. Can you explain this answer?

Ujwal Iyer answered
Given:
  • The Women in the group are divided into groups based on 2 parameters:
    • Employment (Employed, Unemployed)
    • Education (Have a Graduate Degree, Don’t have Graduate Degree)
  • So, the given information can be represented in a table as follows:
  • Now, % of women Unemployed = 100% - 70% = 30%
  • And, % of Women with Graduate Degree = 100% - 25% = 75%
To find: Which of the 3 statements cannot be true?
  • That is, which of the 3 statements are definitely false
Approach:
  1. We’ll evaluate the 3 statements one by one to evaluate which of them are definitely false.
Working Out:
  • Evaluating Statement I
  • No woman in the group who had a graduate degree was unemployed
    • Let the Women with Graduate Degree who are Unemployed be X, and let the Women with Graduate Degree who are Employed be Y.
    • As per this Statement, X = 0%
  • Now, the maximum possible value of Y is 70% (happens when ALL employed women have graduate degrees)
  • So, the minimum possible value of X is 5% (since the sum of Y and X is 75%)
  • Therefore, Statement I is definitely false.
  • Evaluating Statement II
  • Less than half of the women in the group were employed and had a graduate degree
    • Again, Let the women who were employed and had Graduate Degree be Y
    • As per this Statement, Y < 50%
Remember that the question is asking if a Statement is definitely false (that is, false for all possible values of Y)
  • In our analysis of Statement I above, we saw that the maximum possible value of Y is 70%
    • Therefore, for the maximum value of Y, Statement II is false
    • But we cannot say at this point if Statement II is definitely false (that is, false for all possible values of Y)
  • So, let’s now evaluate is also false for the minimum value of Y.
    • The maximum number of Employed Women without Graduate Degree is 25% (happens when ALL women without Graduate Degree are Employed)
​
  • So, the minimum value of Y is 70% - 25% = 45%
  • We observe that for the minimum value of Y, Statement II is true.
  • Thus, Statement II is true for some values of Y and false for other values of Y.
     
  • So, Statement II is not definitely false.
 
  • Evaluating Statement III
  • The number of unemployed women with a graduate degree was 50 percent greater than the number of employed women without a graduate degree
    • Let the Women with Graduate Degree who are Unemployed be X, and let the Women without Graduate Degree who are Employed be Z.
    • As per Statement III, X = 1.5Z
  • Note that this Statement will be definitely false if no valid pair of (X,Z) satisfies the equation X = 1.5Z
  • We will first find the values of X and Z that will satisfy this equation as well as the table above. Then, we will check if these values are acceptable.
  • So, the equation that we can write to relate X and Z is:
    • X = 75% - (70% - Z)
      • = 5% + Z
    • Let’s now substitute X = 1.5Z in this equation:
      • 1.5Z = 5% + Z
      • So, 0.5Z = 5%
      • Therefore, Z = 10%
      • Corresponding value of X = 1.5*10% = 15%
         
  • So, X = 1.5Z is satisfied by X = 15% and Z = 10%
  • We now need to check if these values of X and Z are acceptable
    • The minimum possible value of Z is 0%.
    • In this case, the table will look as under:
The maximum possible value of Z is 25%. In this case, the table will look as under:
  • So, the values of Z range from 0% to 25% and correspondingly, the values of X range from 5% to 30%
  • So, the values X = 15% and Z = 10% do indeed fall in the acceptable range of values of X and Z.
  • So, Statement III is true for one particular pair of X and Z
  • Therefore, Statement III is not definitely false
 
  • Getting to the answer
    • We’ve seen above that out of Statements I, II and III, only Statement I is definitely false.
Looking at the answer choices, we see that the correct answer is Option A

Consider the following statements:
1. A = {1, 3, 5} and B = {2, 4, 7} are equivalent sets.
2. A = {1, 5, 9} and B = {1, 5, 5, 9, 9} are equal sets.
Which of the above statements is/are correct?
  • a)
    1 only
  • b)
    2 only
  • c)
    Neither 1 nor 2
  • d)
    Both 1 and 2
  • e)
    Either 1 or 2
Correct answer is option 'D'. Can you explain this answer?

Bhavya Tiwari answered
Understanding Equivalent Sets
Equivalent sets are sets that have the same number of elements, regardless of what those elements are.
- Statement 1: A = {1, 3, 5} and B = {2, 4, 7}
- Both sets A and B contain 3 elements each.
- Therefore, these sets are equivalent.
Equality of Sets
Equal sets are sets that contain exactly the same elements, including duplicates.
- Statement 2: A = {1, 5, 9} and B = {1, 5, 5, 9, 9}
- Set A contains the elements 1, 5, and 9.
- Set B, although it lists 5 and 9 twice, still contains the same unique elements: 1, 5, and 9.
- Hence, sets A and B are equal.
Conclusion
Both statements are correct:
- Statement 1 is true because the sets are equivalent.
- Statement 2 is true because the sets are equal.
Thus, the correct answer is option 'D': Both 1 and 2.

If A is a subset of B and B is a subset of C, then the cardinality of A ∪ B ∪ C is equal to:
  • a)
    Cardinality of B.
  • b)
    Cardinality of C.
  • c)
    Cardinality of A.
  • d)
    none of the above
  • e)
    can not be determined
Correct answer is option 'B'. Can you explain this answer?

Mihir Chaudhary answered
If A is a subset of B and B is a subset of C, then the cardinality of A must be less than or equal to the cardinality of B, and the cardinality of B must be less than or equal to the cardinality of C.

Of the 120 volunteers who registered for a social welfare camp, 40 stayed for the first half of the camp duration while 10 stayed throughout the camp.  If the number of volunteers who stayed for the second half is twice the number of volunteers who did not turn up for the camp at all, how many volunteers stayed for the second half of the camp?     
  • a)
    40
  • b)
    50
  • c)
    60
  • d)
    80
  • e)
    100
Correct answer is option 'C'. Can you explain this answer?

Prashanth Chawla answered
Step 1: Question statement and Inferences
We are given that 120 volunteers registered for a social welfare camp. On the basis of their appearance in the first or second half of the camp, the volunteers can be divided into the following categories:
Z = the number of volunteers who stayed for only the first half    
Y = the number of volunteers who stayed for only the second half 
X = the number of volunteers who stayed for both the first and the second halves 
T = the number of volunteers who did not show up
Since the total number of volunteers is 120, we can write:
X + Y + Z + T = 120 . . . (1)
Also, it is given in the question that:
X = 10 . . . (2)
X + Z = 40
By substituting the value of X in the above equation, we get:
10 + Z = 40
Z = 30 . . . (3)
Also, we are given:
X + Y = 2T
Substituting the value of X in this equation, we get:
10 + Y = 2T
Or, T= (Y + 10)/2   . . . (4)
Step 2: Finding required values
Substituting Equations 2, 3 and 4 in Equation 1:
 2Y + Y + 10 = 160
 3Y = 150
 Y = 50
Step 3: Calculating the final answer
The number of volunteers who stayed for the second half = Y + 10 = 50 + 10 = 60
Answer: Option (C)

If set A = {1, 3, 5, 7}, set B = {1, 4, 7}, find the value of A − B.
  • a)
    {1, 3, 5}
  • b)
    {3, 5, 7}
  • c)
    {4}
  • d)
    {3, 5}
  • e)
    none of these
Correct answer is option 'D'. Can you explain this answer?

Diya Iyer answered
Understanding the Operation A - B
To find the value of A - B (the difference between sets A and B), we need to understand what this operation entails. The difference A - B consists of all the elements that are in set A but not in set B.
Given Sets
- Set A = {1, 3, 5, 7}
- Set B = {1, 4, 7}
Identifying Elements in A Not in B
1. Start with the elements of set A:
- 1: This is in set B, so we exclude it.
- 3: This is not in set B, so we include it.
- 5: This is also not in set B, so we include it.
- 7: This is in set B, so we exclude it.
Resulting Set A - B
After evaluating each element from set A:
- The remaining elements are 3 and 5.
Thus, A - B = {3, 5}.
Conclusion
The correct answer is option 'D': {3, 5}. The other answer choices do not correctly represent the elements remaining in set A after excluding those found in set B.

If the Cartesian product of two sets A and B(A × B) = {(3, 2), (3, 4), (5, 2), (5, 4)}, find set A.
  • a)
    {3, 2}
  • b)
    {3, 4}
  • c)
    {3, 3}
  • d)
    {3, 5}
  • e)
    None of these
Correct answer is option 'D'. Can you explain this answer?

Ciel Knowledge answered
Given:
Cartesian product of two sets A and B: A × B = {(3, 2), (3, 4), (5, 2), (5, 4)}
Concept used: 
In a Cartesian product A × B, the first element of each ordered pair belongs to set A, and the second element belongs to set B.
Calculation:
From the given Cartesian product A × B, we can extract the elements of set A:
A = {3, 5}
∴ The set A is {3, 5}.

In every (n + 1) - - elementic subset of the set (1, 2, 3, .......2n) which of the following is correct:
  • a)
    exist at least three natural number which are prime to each other
  • b)
    There exist no consecutive natural number
  • c)
    There exist at least two natural numbers which are prime to each other
  • d)
    There exist more than two natural numbers which are prime to each other
  • e)
    None of the above
Correct answer is option 'C'. Can you explain this answer?

Samridhi Nair answered

Explanation:

Given set: (1, 2, 3, .......2n)

a) Existence of at least three natural numbers which are prime to each other:
- In a set of (n-1) elements, it is not guaranteed that there will be at least three numbers that are prime to each other. This cannot be generalized for all subsets.

b) Absence of consecutive natural numbers:
- While it is true that consecutive natural numbers do not exist in a (n-1) element subset, this does not guarantee the existence of prime numbers.

c) Existence of at least two natural numbers which are prime to each other:
- By the Pigeonhole Principle, in any subset of (n-1) elements taken from a set of 2n elements, there will be at least one pair of numbers that are relatively prime to each other.

d) Existence of more than two natural numbers which are prime to each other:
- The question does not specify that there will be more than two numbers that are prime to each other in any given subset. Therefore, this statement cannot be concluded.

e) None of the above:
- The correct answer is option 'C' because the existence of at least two natural numbers that are prime to each other can be guaranteed in any (n-1) element subset of the given set.

For any set A, (A')' is equal to:
  • a)
    A
  • b)
    A'
  • c)
    φ
  • d)
    (A')'
  • e)
    none of thes
Correct answer is option 'A'. Can you explain this answer?

Manish Aggarwal answered
Calculation:
Complement of A = (A') = All elements not in A
Complement of A'
((A')') = All elements not in A', which are the elements in A.
Therefore, (A')' = A.

In College X in the United States, there are 200 students in a class, of which  80 are female. If 10% of the class consists of female non-American students and 3/5th of the class are American students, how many of the students in the class are male American students?
  • a)
    20
  • b)
    40
  • c)
    60
  • d)
    80
  • e)
    120
Correct answer is option 'C'. Can you explain this answer?

Soumya Iyer answered
Given
  • Number of students in the class = 200
  • Number of female students = 80
    • So, number of male students = 200 – 80 = 120
  • Number of female non-American students = 10% of 200 = 20
  • Number of American students = 3/5 * 200 = 120
 
To Find: Number of students who are male Americans?

Approach
1. To find the number of male americans, we will use the relation:
  1. Number of American students = Number of female American students + Number of male American students             
  2. We know the number of American students, but we do not know the number of female American students.
  3. So, we need to find the number of female American students
2. Now, Number of female students = Number of female American students + Number of female non-American students
  1. As we know the number of female students and the number of female non-American students, we can calculate the the number of female American students
 
Working Out
  1. Number of female students = 80
    1. Number of female non-American students = 20
    2. Number of female American students = 80 – 20 = 60
 
  1. Number of American students = 120
    1. Number of female American students = 60 (calculated above)
    2. So, Number of male American students = 120 – 60 = 60
So, there are 60 male American students.
Answer: C

The human resources manager of a company compiled the data that the company had on the academic qualifications of its 100 employees. He observed that employees who had an Engineering and an MBA degree were the most in number and employees who had neither an Engineering nor an MBA degree were the least in number. If there were 20 employees who had an Engineering degree, but not an MBA degree, which of the following cannot be the number of employees who had an MBA degree?
  • a)
    55
  • b)
    65
  • c)
    75
  • d)
    80
  • e)
    None of the above
Correct answer is option 'A'. Can you explain this answer?

Gauri Iyer answered
Given
  • Number of employees = 100
     
  • Let us assume:
    • Number of employees who only have an MBA degree = c.
    • Number of employees who have both an MBA and an Engineering degree = b.
    • Number of employees who do neither have an MBA nor an Engineering degree = d.
       
  • Employees having neither Engineering nor an MBA were the least in number.
    • So d is the least in the number out of 20,b, c & d.
       
  • Number of employees who had an Engineering degree and not an MBA degree = 20
To Find: Among the options, which of them cannot be the number of employees who had an MBA degree?

Approach
  1. Let’s first draw the venn diagram to understand the information given
 
2. We need to find the possible range of values of employees who had an MBA degree = b + c
  1. So, we need to find the maximum and minimum value of b + c
3. As we know that total number of employees is 100 and d is minimum number of employees possible, we will use this information to find out the range of values of b + c

Working Out
  1. As the total number of employees = 100
    1. 20 + b + c + d = 100
    2. b + c + d = 80
       
  2. Maximum value of b + c
    1. Maximum value of b + c is possible, when d is minimum
    2. As the minimum value of d = 0, maximum value of b + c = 80…….(1)
       
  3. Minimum value of b + c
    1. b + c will be minimum , when d is maximum
    2. Since we know the number of employees who had only an Engineering degree = 20, d < 20
    3. So, maximum value of d = 19 (remember that out of 20, b, c and d, we are given that d holds the minimum value. So, d must be less than 20)
    4. Hence, minimum value of b + c = 80 – 19 = 61…….(2)
       
  4. Using (1) and (2), we can write 61 ≤ b + c ≤ 80
     
  5. The only value in the options that does not lie in the range is 55, option A
 
Answer: A

If A = {x, y, z}, then the number of subsets in powerset of A is
  • a)
    8
  • b)
    7
  • c)
    9
  • d)
    6
  • e)
    none of these
Correct answer is option 'A'. Can you explain this answer?

Manish Aggarwal answered
Given, A = {x, y, z}. 
The power set (or powerset) of a Set A is defined as the set of all subsets of the Set A including the Set itself and the null or empty set.
Powerset of A = {ϕ,{x}, {y}, {z}, {x, y}, {y, z}, {x, z},{x, y, z}}.
Hence, the number of subsets in the powerset of A is 8.

In a locality, for every person, who owns only a car, there are 3 people who own only a bike. The number of people who own both a car and a bike is half the number of people who either own only a car or only a bike. If the number of people who neither own a car nor a bike is equal to the number of people who own a bike, which of the following can be the total number of people in the locality?
  • a)
    27
  • b)
    40
  • c)
    66
  • d)
    105
  • e)
    None of the above
Correct answer is option 'C'. Can you explain this answer?

Athul Joshi answered
Given
  • Let the number of people who own only a car be x
    • So, number of people who own only a bike = 3x
    • Also, since x denotes the number of people, x must be a non-negative integer
  • Number of people who own a car and a bike = ½ *(Number of people who own either a bike or a only car) = ½ * (x+3x) = 2x
  • Number of people who neither own a car nor a bike = Number of people who own a bike
To Find: Among the options, which can be the total people in the locality?
Approach
  1. We will try to express the number of people in terms of x through the venn diagram and then evaluate the possible options.
Working Out
 
  1. Number of people who own a bike = 3x + 2 x = 5x
    1. So, the number of people who own neither a bike nor a car = 5x
  2. Hence, total people in the locality = 3x + 2x + x + 5x = 11x
    1. So, the total people in the locality should be a multiple of 11
    2. The only multiple of 11 in the options is 66, option C
 
Answer: C

The table above shows the research data gathered from a group of rural and urban residents. What is the number of rural residents who own a car?
(1) The number of rural residents in the group is 60% of the number of urban residents in the group.
(2) The difference between the number of urban residents who own a car and the number of rural residents who own a car is one-fifth of the number of rural and urban residents in the group.
  • a)
    Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
  • b)
    Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
  • c)
    BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
  • d)
    EACH statement ALONE is sufficient to answer the question asked.
  • e)
    Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?

Soumya Iyer answered
Let the number of rural residents who own a car = p
STATEMENT 1: The number of rural residents in the group is 60% of the number of urban residents in the group.
Let the number of urban residents = x
Then, number of rural residents = 0.6x
We know that, total number of people = number of people who own a car + number of people who don't own a car = number of urban residents + rural residents
total = (15 + p) + 18 (given in the question) = x + 0.6x
We have two variables x and p but only 1 equation.
Insufficient
STATEMENT 2: The difference between the number of urban residents who own a car and the number of rural residents who own a car is one-fifth of the number of rural and urban residents in the group.
Two equations can be formed here:
1) 15 - p = 1/5(rural + urban) or
2) p-15 = 1/5(rural + urban)
Both will give different answers of p
Insufficient
COMBINING BOTH STATEMENTS:
1) 15 - p = 1/5 (rural + urban)
75 - 5p = rural + urban
75 - 5p = 0.6x + x
75 - 5p = 15 + p + 18 (from statement 1)
42 = 6p
p = 7
2) p - 15 = 1/5 (rural + urban)
5p - 75 = 15 + p + 18
4p = 108
p = 27
We have two values of p.
Let's put it in equation 1 and get the value of x (the number of urban residents)
For p = 7,
15 + p + 18 = 1.6 x
33 + 7 = 1.6x
x = 25
For p = 27,
15 + p + 18 = 1.6 x
33 + 27 = 1.6x
1.6 x = 60
x = 75/2 = 37.5 INVALID
The value of x represents number of people and cannot be a fraction. Therefore, there is only one unique value of x and that is x = 25 when p = 7
Thus, (C) is sufficient.

A ∪ (B ∩ C) = ____________
  • a)
    A ∩ (B ∪ C) 
  • b)
    A ∪ (B ∪ C)
  • c)
    (A ∪ B) ∪ (A ∪ C)
  • d)
    (A ∪ B) ∩ (A ∪ C)
  • e)
    None of these
Correct answer is option 'D'. Can you explain this answer?

Tarun Kaushik answered
Given:
The expression is A ∪ (B ∩ C)
We use the concept of set theory.
According to the distributive laws of sets, A ∪ (B ∩ C) is equivalent to (A ∪ B) ∩ (A ∪ C).
∴ The correct option is (D) (A ∪ B) ∩ (A ∪ C).

All the employees of Company X were appraised at the year end. 40% of the employees got a promotion, 50% of the employees got a salary hike and 30% of the employees neither got a promotion nor got a salary hike. If there were 40 employees who got both the promotion and the salary hike, what was the number of employees in the company?
  • a)
    100
  • b)
    120
  • c)
    150
  • d)
    200
  • e)
    250
Correct answer is option 'D'. Can you explain this answer?

Janani Sharma answered
Given
  • Percentage of employees who got a promotion = 40%
  • Percentage of employees who got a salary hike = 50%
  • Percentage of employees who neither got a promotion nor a salary hike = 30%
  • Number of employees who got both the promotion and the salary hike = 40
To Find: Number of employees in the company?

Approach
  1. To find the total number of employees in the company, we will try to express the number of employees who got both the promotion and the salary hike(i.e. 40), as a percentage of the total employees of the company.
     
Total employees in the company = Employees who got only salary hike + Employees who got only promotion + Employees who got salary hike and promotion + Employees who got neither salary hike nor promotion
  1. Adding “Employees who got salary hike and promotion on both sides” we have
  2. Total employees in the company + Employees who got salary hike and promotion = (Employees who got only salry hike + Employees who got salary hike and promotion)+ (Employees who got only promotion + Employees who got salary hike and promotion) + Employees who got neither salary hike nor promotion
  3. Total employees in the company + Employees who got salary hike and promotion = Employees who got a salary hike+  Employees who got a promotion  + Employees who got neither salary hike nor promotion
  4. From the above equation, we can find the percentage of employees who got salary hike and promotion
Working Out
  1. Total employees in the company + Employees who got salary hike and promotion = Employees who got a salary hike+  Employees who got a promotion  + Employees who got neither salary hike nor promotion
    a.  100% + Employees who got salary hike and promotion = 50% + 40% + 30%
    b.  Employees who got salary hike and promotion = 20%
     
  2. Now, we know that employees who got salary hike and promotion = 40
    1. So, if 20% is 40, 100% = 200
Hence, the total number of employees in the company = 200

Answer: D

Chapter doubts & questions for Sets - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Sets - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam. Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.

35 Days Preparation for GMAT

191 videos|289 docs|197 tests

Top Courses GMAT

© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily