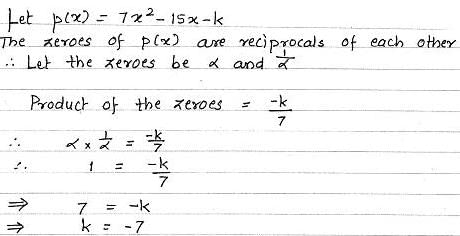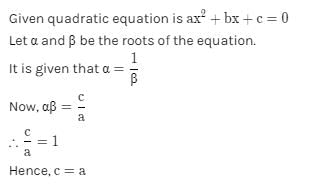All Exams >
Grade 9 >
Mathematics: Algebra 2 >
All Questions
All questions of Polynomial Equations for Grade 9 Exam
Can you explain the answer of this question below: If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:- A:14/25
- B:7/5
- C:2/5
- D:7/2
The answer is d.
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:
A:
14/25
B:
7/5
C:
2/5
D:
7/2
|
Anshu Shah answered |
We have 2 find (1/α + 1/β)
now 1/α + 1/β = (α + β)/ α β (taking LCM)
now by the given poly. we get
(α + β) = -b/a = 7/5
α β = c/a = 2/5
so, (α + β)/ α β = (7/5) / (2/5)
= 7/2
So, 1/α + 1/β = (α + β)/ α β = 7/2
Hence, 1/α + 1/β = 7/2
If one of the factors of x2 + x – 20 is (x + 5), then other factor is- a)(x – 4)
- b)(x – 5)
- c)(x – 6)
- d)(x – 7)
Correct answer is 'A'. Can you explain this answer?
If one of the factors of x2 + x – 20 is (x + 5), then other factor is
a)
(x – 4)
b)
(x – 5)
c)
(x – 6)
d)
(x – 7)
|
Arun Sharma answered |
Using mid-term splitting,
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
x2+x-20=x2+5x-4x-20=x(x+5)-4(x+5)
Taking common x+5
(x+5)(x-4) , so the other factor is x-4
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
- a)6
- b)7
- c)8
- d)9
Correct answer is option 'A'. Can you explain this answer?
If p and q are the zeroes of the polynomial x2- 5x + k. Such that p - q = 1, find the value of K
a)
6
b)
7
c)
8
d)
9
|
Zachary Foster answered |
Given α and β are the zeroes of the polynomial x2 − 5x + k
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
Also given that α − β = 1 → (1)
Recall that sum of roots (α + β) = −(b/a)
∴ α + β = 5 → (2)
Add (1) and (2), we get
α − β = 1
α + β = 5
2α = 6
∴ α = 3
Put α = 3 in α + β = 5
3 + β = 5
∴ β = 2
Hence 3 and 2 are zeroes of the given polynomial
Put x = 2 in the given polynomial to find the value of k ( Since 2 is a zero of the polynomial, f(2) will be 0 )
x2 − 5x + k = 0
⇒ 22 − 5(2) + k = 0
⇒ 4 − 10 + k = 0
⇒ − 6 + k = 0
∴ k = 6
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =- a)2
- b)3
- c)1
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2 – 3x – x2, then α + β =
a)
2
b)
3
c)
1
d)
None of these
|
Pooja Shah answered |
If α and β are the zeros of the polynomial then
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
(x−α)(x−β) are the factors of the polynomial
Thus, (x−α)(x−β) is the polynomial.
So, the polynomial =x2 − αx − βx + αβ
=x2 − (α + β)x + αβ....(i)
Now,the quadratic polynomial is
2 − 3x − x2 = x2 + 3x − 2....(ii)
Now, comparing equation (i) and (ii),we get,
−(α + β) = 3
α + β = −3
−(α + β) = 3
α + β = −3
What value/s can x take in the expression k(x – 10) (x + 10) =0 where k is any real number.- a)100, -100
- b)Infinitely many
- c)Depends on value of k
- d)10, -10
Correct answer is option 'D'. Can you explain this answer?
What value/s can x take in the expression k(x – 10) (x + 10) =0 where k is any real number.
a)
100, -100
b)
Infinitely many
c)
Depends on value of k
d)
10, -10
|
|
Avinash Patel answered |
k(x – 10) (x + 10) =0
⇒ either k=0
Or x-10=0
Or x+10=0
Since we don’t know the value of k
So either x-10=0
x=10
Or x+10=0
x=-10
So values of x can be 10,-10
⇒ either k=0
Or x-10=0
Or x+10=0
Since we don’t know the value of k
So either x-10=0
x=10
Or x+10=0
x=-10
So values of x can be 10,-10
If “1” is a zero of the polynomial P(a) = x2a2 – 2xa + 3x – 2 , then x = ______
- a)2
- b)-2, 1
- c)+2, -2
- d)-2, 0
Correct answer is option 'B'. Can you explain this answer?
If “1” is a zero of the polynomial P(a) = x2a2 – 2xa + 3x – 2 , then x = ______
a)
2
b)
-2, 1
c)
+2, -2
d)
-2, 0
|
|
Pooja Shah answered |
The correct solution of this question is given below:
Here, P(a) = x2a2 - 2xa + 3x - 2
1 is a zero of P(a), so P(1) = 0
Therefore, x212 - 2x.1 + 3x - 2 = 0
x2 + x - 2 = 0
(x + 2)(x - 1) = 0
x = -2, 1
A polynomial of degree three is called ……- a)cubic polynomial
- b)quadratic polynomial
- c)linear polynomial
- d)zero polynomial
Correct answer is option 'A'. Can you explain this answer?
A polynomial of degree three is called ……
a)
cubic polynomial
b)
quadratic polynomial
c)
linear polynomial
d)
zero polynomial
|
Maitri Kulkarni answered |
A cubic polynomial is a polynomial of the form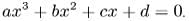 
. A cubic polynomial is a polynomial of degree 3. A univariate cubic polynomial has the form . An equation involving a cubic polynomial is called a cubic equation. A closed-form solution known as the cubic formula exists for the solutions of an arbitrary cubic equation.
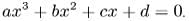. A cubic polynomial is a polynomial of degree 3. A univariate cubic polynomial has the form . An equation involving a cubic polynomial is called a cubic equation. A closed-form solution known as the cubic formula exists for the solutions of an arbitrary cubic equation.Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –- a)x2 – 5x – 14
- b)x2 – 10x – 14
- c)x2 – 5x + 14
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Quadratic polynomial having sum of it's zeros 5 and product of it's zeros – 14 is –
a)
x2 – 5x – 14
b)
x2 – 10x – 14
c)
x2 – 5x + 14
d)
None of these
|
|
Amit Kumar answered |
The quadratic equation is of the form x2 - (sum of zeros) x + (product of zeros)
=x2 - 5x - 14
=x2 - 5x - 14
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :- a)5, 6
- b)- 5, - 6
- c)- 5, 6
- d)5, - 6
Correct answer is option 'C'. Can you explain this answer?
If x = 2 and x = 3 are zeros of the quadratic polynomial x2 + ax + b, the values of a and b respectively are :
a)
5, 6
b)
- 5, - 6
c)
- 5, 6
d)
5, - 6
|
Gaurav Kumar answered |
Zeros of the polynomials are the values which gives zero when their value is substituted in the polynomial
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
When x=2,
x2+ax+b =(2)2+a*2+b=0
4+2a+b=0
b=-4-2a ….1
When x=3,
(3)2+ 3a + b=0
9 + 3a + b=0
Substituting
9 + 3a - 4 - 2a =0
5 + a =0
a = -5
b = 6
Find the quadratic polynomial whose zeros are 2 and -6
- a)x2 + 4x + 12
- b)x2 – 4x – 12
- c)x2 + 4x – 12
- d)x2 – 4x + 12
Correct answer is option 'C'. Can you explain this answer?
Find the quadratic polynomial whose zeros are 2 and -6
a)
x2 + 4x + 12
b)
x2 – 4x – 12
c)
x2 + 4x – 12
d)
x2 – 4x + 12
|
Naina Sharma answered |
We know that quadratic equation is of the form x2-(sum of zeros)x+product of zeros
Sum of zeros=2-6=-4
Product of zeros=2*(-6)=-12
x2-(sum of roots )x + product of roots
x2-(-4)x + 12
x2+4x-12
So the equation is x2+4x-12
Sum of zeros=2-6=-4
Product of zeros=2*(-6)=-12
x2-(sum of roots )x + product of roots
x2-(-4)x + 12
x2+4x-12
So the equation is x2+4x-12
Find the sum and the product of the zeroes of the polynomial: x2-3x-10- a)3, 10
- b)-3, -10
- c)3,-10
- d)-3, 10
Correct answer is option 'C'. Can you explain this answer?
Find the sum and the product of the zeroes of the polynomial: x2-3x-10
a)
3, 10
b)
-3, -10
c)
3,-10
d)
-3, 10
|
Raghav Bansal answered |
X²-3x-10
x² -(5x-2x)-10
x² - 5x+2x-10
x(x-5)+2(x-5)
(x-5)(x+2)
x=5
x=-2
Sum of zeroes = α+β = 5-2 = 3
α+β = -b/a = -(-3)/1 = 3
Product of zeroes = αβ = 5*-2 = -10
αβ = c/a = -10/1 = -10
x² -(5x-2x)-10
x² - 5x+2x-10
x(x-5)+2(x-5)
(x-5)(x+2)
x=5
x=-2
Sum of zeroes = α+β = 5-2 = 3
α+β = -b/a = -(-3)/1 = 3
Product of zeroes = αβ = 5*-2 = -10
αβ = c/a = -10/1 = -10
The number of polynomials having zeroes -2 and 5 is:- a)1
- b)3
- c)2
- d)more than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeroes -2 and 5 is:
a)
1
b)
3
c)
2
d)
more than 3
|
|
Amit Kumar answered |
Since the question doesn’t say that there are only 2 zeros of the polynomial we , there can be n number of polynomials which have two of its zeros as -2 and 5 .So the correct answer is more than 3.
The number of polynomials having zeroes as -2 and 5 is:- a)1
- b)2
- c)3
- d)More than 3
Correct answer is option 'D'. Can you explain this answer?
The number of polynomials having zeroes as -2 and 5 is:
a)
1
b)
2
c)
3
d)
More than 3
|
Kamna Science Academy answered |
The polynomials x2-3x-10, 2x2-6x-20, (1/2)x2-(3/2)x-5, 3x2-9x-30, have zeroes as -2 and 5.
If sum of the zeroes of the polynomial is 4 and their product is 4, then the quadratic polynomial is- a)x2 – 2x + 2
- b)x2 – 4x + 4
- c)x2 + 4x + 4
- d)x2 + 2x + 2
Correct answer is option 'B'. Can you explain this answer?
If sum of the zeroes of the polynomial is 4 and their product is 4, then the quadratic polynomial is
a)
x2 – 2x + 2
b)
x2 – 4x + 4
c)
x2 + 4x + 4
d)
x2 + 2x + 2
|
|
Naina Sharma answered |
Sum of zeros= α+β =4
Product of zeros=αβ=4
We have Quadratic equation as
x2-(Sum of zeros)x+Product of zeros
=x2-4x+4
Product of zeros=αβ=4
We have Quadratic equation as
x2-(Sum of zeros)x+Product of zeros
=x2-4x+4
If the point (5,0) , (0-2) and (3,6) lie on the graph of a polynomial . Then which of the following is a zero of the polynomial?- a)5
- b)6
- c)not defined
- d)-2
Correct answer is option 'A'. Can you explain this answer?
If the point (5,0) , (0-2) and (3,6) lie on the graph of a polynomial . Then which of the following is a zero of the polynomial?
a)
5
b)
6
c)
not defined
d)
-2
|
Sanaya sharma answered |
Explanation:
Since, a zero of a polynomial always lies on the x-axis as a point. In the given question the point (5,0) is a point that lies on x-axis, so its corresponding x value represents zero of the polynomial.
Therefore, 5 is the zero of the polynomial.
Hence, the correct option is A.
You can know more about Geometrical Meaning of the Zeroes of a Polynomial through the document:
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :- a) x2 + 3x – 2
- b)x2 – 2x + 3
- c)x2 – 3x + 2
- d)x2 – 3x – 2
Correct answer is 'C'. Can you explain this answer?
The quadratic polynomial whose sum of zeroes is 3 and product of zeroes is –2 is :
a)
x2 + 3x – 2
b)
x2 – 2x + 3
c)
x2 – 3x + 2
d)
x2 – 3x – 2
|
|
Pooja Shah answered |
Sum of zeros = 3/1
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
-b/a = 3/1
Product of zeros = 2/1
c/a = 2/1
This gives
a = 1
b = -3
c = -2,
The required quadratic equation is
ax2+bx+c
So, x2-3x+2
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.- a)12
- b)-12
- c)14
- d)-14
Correct answer is option 'A'. Can you explain this answer?
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.
a)
12
b)
-12
c)
14
d)
-14
|
|
Shantala nair answered |
p (x)= x^2-8x+k
p (x)=Ax^2+Bx+C(The equation is in this form)
p (x)=Ax^2+Bx+C(The equation is in this form)
Let the zeroes be 'a' and 'b'
It is given that
=> a^2+b^2=40
=> (a+b)^2 - 2ab = 40 ----1
=> a^2+b^2=40
=> (a+b)^2 - 2ab = 40 ----1
sum of zeroes
=> a+b = -B/A = -(-8)/1 = 8
=> a+b = -B/A = -(-8)/1 = 8
Product of zeroes
=> a*b = C/A = k
=> a*b = C/A = k
Substitute these values in the equation1 we get
=> 8^2 - 2k = 40
=> 64 - 2k = 40
=> 2k = 24
=> k = 12
=> 8^2 - 2k = 40
=> 64 - 2k = 40
=> 2k = 24
=> k = 12
Therefore the value of k is 12
If -√5 and √5 are the roots of the quadratic polynomial. Find the quadratic polynomial.- a)x-5
- b)(x-5)(x+5)
- c)x2 – 5
- d)x2 – 25
Correct answer is option 'C'. Can you explain this answer?
If -√5 and √5 are the roots of the quadratic polynomial. Find the quadratic polynomial.
a)
x-5
b)
(x-5)(x+5)
c)
x2 – 5
d)
x2 – 25
|
Vikram Kapoor answered |
We have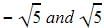 
as the roots which means x + 
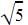and x- 
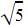are the factors of the quadratic equation. Multiplying x+ 
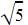and x- 
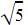and applying a2-b2 we get the equation x2-5.
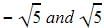as the roots which means x + 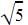and x- 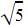are the factors of the quadratic equation. Multiplying x+ 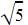and x- 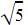and applying a2-b2 we get the equation x2-5.If one zero of 2x2 – 3x + k is reciprocal to the other, then the value of k is :- a)2
- b)-2/3
- c)-3
- d)-3/2
Correct answer is option 'A'. Can you explain this answer?
If one zero of 2x2 – 3x + k is reciprocal to the other, then the value of k is :
a)
2
b)
-2/3
c)
-3
d)
-3/2
|
|
Rajiv Gupta answered |
Given: 2x^2-3x+k ....eq 1
Let the 2 zeroes be α & 1/α
Quadratic form : ax^2+bx+c....eq 2
On comparing eq 1 & eq 2 we get
a=2 ,b = -3, c= k
Product of zeroes = α x 1/α = 1
Product of zeroes= c/a
1= k/ 2
K= 2
The value of k is 2.
Sum and the product of zeroes of the polynomial x2 +7x +10 is - a)10/7 and -10/7
- b)7/10 and -7/10
- c)-7 and 10
- d)7 and -10
Correct answer is option 'C'. Can you explain this answer?
Sum and the product of zeroes of the polynomial x2 +7x +10 is
a)
10/7 and -10/7
b)
7/10 and -7/10
c)
-7 and 10
d)
7 and -10
|
|
Ananya Das answered |
x2 + 7x + 10 = (x + 2)(x + 5)
So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0
Therefore, the zeroes of x2 + 7x + 10 are –2 and –5.
Sum of zeroes = -7 = –(Coefficient of x) / (Coefficient of x2)
Product of zeroes = 10 = Constant term / Coefficient of x2
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =- a)- 2
- b)- 1
- c)1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If α,β be the zeros of the quadratic polynomial 2x2 + 5x + 1, then value of α + β + αβ =
a)
- 2
b)
- 1
c)
1
d)
None of these
|
|
Naina Sharma answered |
P(x) = 2x² + 5x + 1
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Sum of roots = -5/2
Product of roots = 1/2
Therefore substituting these values,
α + β +αβ
=(α + β) + αβ
= -5/2 + 1/2
= -4/2
= -2
Find the sum and the product of zeroes of the polynomial x2 +7x +10- a)7,-10
- b)7, 10
- c)-7,-10
- d)-7, 10
Correct answer is option 'D'. Can you explain this answer?
Find the sum and the product of zeroes of the polynomial x2 +7x +10
a)
7,-10
b)
7, 10
c)
-7,-10
d)
-7, 10
|
|
Maitri Kulkarni answered |
x2 + 7x + 10 = (x + 2)(x + 5)
So, the value of x2 + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0
Therefore, the zeroes of x2 + 7x + 10 are –2 and –5.
Sum of zeroes = -7 = –(Coefficient of x) / (Coefficient of x2)
Product of zeroes = 10 = Constant term / Coefficient of x2
If α , β are the zeroes of f(x) = px2 – 2x + 3p and α + β = αβ then the value of p is:- a)1/3
- b)-2/3
- c)2/3
- d)-1/3
Correct answer is option 'C'. Can you explain this answer?
If α , β are the zeroes of f(x) = px2 – 2x + 3p and α + β = αβ then the value of p is:
a)
1/3
b)
-2/3
c)
2/3
d)
-1/3
|
|
Ananya Das answered |
The given polynomial is
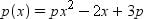
Also, α and β are the zeros of p(x).
and α + β = α × β
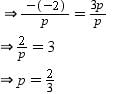
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:- a)14/25
- b)7/5
- c)2/5
- d)7/2
Correct answer is 'D'. Can you explain this answer?
If α and β are the zeroes of the polynomial 5x2 – 7x + 2, then sum of their reciprocals is:
a)
14/25
b)
7/5
c)
2/5
d)
7/2
|
Anisha Mukherjee answered |
We have 2 find (1/α + 1/β)
now 1/α + 1/β = (α + β)/ α β (taking LCM)
now by the given poly. we get
(α + β) = -b/a = 7/5
α β = c/a = 2/5
so, (α + β)/ α β = (7/5) / (2/5)
= 7/2
So, 1/α + 1/β = (α + β)/ α β = 7/2
Hence, 1/α + 1/β = 7/2
If p(x) is a polynomial of degree one and p(a) = 0, then a is said to be:- a)Zero of p(x)
- b)Value of p(x)
- c)Constant of p(x)
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If p(x) is a polynomial of degree one and p(a) = 0, then a is said to be:
a)
Zero of p(x)
b)
Value of p(x)
c)
Constant of p(x)
d)
None of the above
|
Kds Coaching answered |
If p(x) is a polynomial of degree one, it can be written as:
p(x) = mx + c
where m and c are constants, and m ≠ 0.
Given that p(a) = 0, substituting x = a into p(x):
p(a) = m(a) + c = 0
This equation implies that a is a root or zero of the polynomial p(x), as it satisfies p(a) = 0.
Hence, the correct answer is:
A: Zero of p(x)
p(x) = mx + c
where m and c are constants, and m ≠ 0.
Given that p(a) = 0, substituting x = a into p(x):
p(a) = m(a) + c = 0
This equation implies that a is a root or zero of the polynomial p(x), as it satisfies p(a) = 0.
Hence, the correct answer is:
A: Zero of p(x)
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –- a)x2 + 2x + 3
- b)x2 – 5x + 3
- c)x2 + 5x + 3
- d)x2 + 3x – 5
Correct answer is option 'C'. Can you explain this answer?
The sum and product of zeros of the quadratic polynomial are – 5 and 3 respectively the quadratic polynomial is equal to –
a)
x2 + 2x + 3
b)
x2 – 5x + 3
c)
x2 + 5x + 3
d)
x2 + 3x – 5
|
Bhaskar Dasgupta answered |
If α, β be the zeros of the quadratic polynomial ,then
(x−α)(x−β) is the quadratic polynomial.
Thus, (x−α)(x−β) is the polynomial.
=x^2−αx−βx+αβ
=x^2−x(α+β)+αβ(i)
(α+β)=−5αβ=3
Now putting the value of (α+β),αβ in equation (i) we get,
x^2−x(−5)+3
=x^2+5x+3
If α, β are zeroes of the polynomial f(x) = x2 + 5x + 8, then value of (α + β) is- a)5
- b)8
- c)-8
- d)-5
Correct answer is option 'D'. Can you explain this answer?
If α, β are zeroes of the polynomial f(x) = x2 + 5x + 8, then value of (α + β) is
a)
5
b)
8
c)
-8
d)
-5
|
|
Arun Sharma answered |
We have quadratic equation of the form
x2 - (sum of zeros) x + product of zeros, so comparing this with the given equation we have sum of zeros = -5
So, α + β = -5
x2 - (sum of zeros) x + product of zeros, so comparing this with the given equation we have sum of zeros = -5
So, α + β = -5
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most –- a)One zero
- b)Two zeros
- c)Three zeros
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most –
a)
One zero
b)
Two zeros
c)
Three zeros
d)
None of these
|
Uday Datta answered |
The polynomial ax^2+bx+c has three terms. The first one is ax^2, the second is bx, and the third is c.
The exponent of the first term is 2.
The exponent of the second term is 1 because bx=bx^1.
The exponent of the third term is 0 because c=cx^0.
Since the highest exponent is 2, therefore, the degree of ax^2+bx+c is 2.
Since, the degree of the polynomial is 2, hence, the polynomial ax^2+bx+c can have zero, one or two zeroes.
Hence, the polynomial ax^2+bx+c can have at most two zereos.
The graph of the polynomial p(x) intersects the x-axis three times in distinct points, then which of the following could be an expression for p(x):- a)4 – 4x – x2 + x3
- b)3x + 3
- c)3x2 + 3x – 3
- d)x2 – 9
Correct answer is option 'A'. Can you explain this answer?
The graph of the polynomial p(x) intersects the x-axis three times in distinct points, then which of the following could be an expression for p(x):
a)
4 – 4x – x2 + x3
b)
3x + 3
c)
3x2 + 3x – 3
d)
x2 – 9
|
|
Radha Iyer answered |
The polynomial intersects the x-axis three times. A point on x-axis is of the form (a,0) where a is any number.So this means that any point on x axis has y coordinate equal to zero and we know that y=0 is when we have roots of the equation.So since there are three points at which y=0 so we have 3 roots of the equation. No. of roots is equal to the degree of the polynomial. So the degree of the polynomial is 3.
If one zero of the polynomial x2 + kx + 18 is double the other zero then k = ?- a)6
- b)± 9
- c)3
- d)±3
Correct answer is option 'B'. Can you explain this answer?
If one zero of the polynomial x2 + kx + 18 is double the other zero then k = ?
a)
6
b)
± 9
c)
3
d)
±3
|
|
Gaurav Kumar answered |
Let one zero of the equation be x
Then, other would be 2x
As we know,
x × 2x = 18
x2 = 9
x = 3, -3
Case 1:
If x = 3, 2x = 6
Therefore, -k = sum of roots = 9
⇒ k = -9
Case 2:
If x = -3, 2x = -6
Therefore, -k = -9
⇒ k = 9
So, k can be 9,-9. Therefore, option 'b' is correct.
Then, other would be 2x
As we know,
x × 2x = 18
x2 = 9
x = 3, -3
Case 1:
If x = 3, 2x = 6
Therefore, -k = sum of roots = 9
⇒ k = -9
Case 2:
If x = -3, 2x = -6
Therefore, -k = -9
⇒ k = 9
So, k can be 9,-9. Therefore, option 'b' is correct.
The sum and product of zeros of a quadratic polynomial are 2 and -15 respectively. The quadratic polynomial is
- a)x2 + 2x – 15
- b)x2 – 2x + 15
- c)x2 – 2x – 15
- d)x2 + 2x + 15
Correct answer is option 'C'. Can you explain this answer?
The sum and product of zeros of a quadratic polynomial are 2 and -15 respectively. The quadratic polynomial is
a)
x2 + 2x – 15
b)
x2 – 2x + 15
c)
x2 – 2x – 15
d)
x2 + 2x + 15
|
Nk Classes answered |
Let the polynomial be f(x).
f(x) = x2− (sum of zeros)x + product of zeros
= x2−2x–15
A quadratic polynomial, whose zeroes are –3 and 4, is- a)x2 – x + 12
- b)x2 + x + 12
- c)(x2/2) – (x/2) – 6
- d)2x2 + 2x – 24
Correct answer is option 'C'. Can you explain this answer?
A quadratic polynomial, whose zeroes are –3 and 4, is
a)
x2 – x + 12
b)
x2 + x + 12
c)
(x2/2) – (x/2) – 6
d)
2x2 + 2x – 24
|
|
Kds Coaching answered |
A quadratic polynomial in terms of the
zeroes
α and β is given byx2 - (sum of the zeroes) x + (product of the zeroes)
i.e, f(x) = x2 -(α + β) x + αβ
Now,
Given that zeroes of a quadratic polynomial are -3 and 4
Let α = -3 and β = 4
Therefore, substituting the value α = -3 and β = 4 inf(x) = x2 -(α + β) x + αβ, we get
f(x) = x2 - ( -3 + 4) x +(-3)(4)
= x2 - x - 12, which is equal to (x2/2) – (x/2) – 6
The graph of the polynomial 2x2-8x+5 cuts the y-axis at - a)(8, 9)
- b)(0, 5)
- c)(0, 7)
- d)(6, 0)
Correct answer is option 'B'. Can you explain this answer?
The graph of the polynomial 2x2-8x+5 cuts the y-axis at
a)
(8, 9)
b)
(0, 5)
c)
(0, 7)
d)
(6, 0)
|
EduRev Class 10 answered |
Clarification: The graph of the polynomial 2x2-8x+5 cuts the y-axis.
Hence, the value of x will be 0.
y(0)=2(0)2-8(0)+5
y=5
The graph cuts the y-axis at (0,5)
Hence, the value of x will be 0.
y(0)=2(0)2-8(0)+5
y=5
The graph cuts the y-axis at (0,5)
A polynomial of degree n has:- a)Only one zero
- b)At least n zeroes
- c)More than n zeroes
- d)At most n zeroes
Correct answer is option 'D'. Can you explain this answer?
A polynomial of degree n has:
a)
Only one zero
b)
At least n zeroes
c)
More than n zeroes
d)
At most n zeroes
|
|
EduRev Class 10 answered |
Maximum number of zeroes of a polynomial = Degree of the polynomial
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is- a)10
- b)–10
- c)5
- d)–5
Correct answer is option 'B'. Can you explain this answer?
If one zero of the quadratic polynomial x2 + 3x + k is 2, then the value of k is
a)
10
b)
–10
c)
5
d)
–5
|
|
Kds Coaching answered |
Given that 2 is the zero of the quadratic polynomial x2 + 3x + k.
⇒ (2)2 + 3(2) + k = 0
⇒ 4 + 6 + k = 0
⇒ k = -10
The zeroes of x2– 2x – 8 are:- a)(2, -4)
- b)(4, -2)
- c)(-2, -2)
- d)(-4, -4)
Correct answer is option 'B'. Can you explain this answer?
The zeroes of x2– 2x – 8 are:
a)
(2, -4)
b)
(4, -2)
c)
(-2, -2)
d)
(-4, -4)
|
|
EduRev Class 10 answered |
x2 – 2x – 8 = x2 – 4x + 2x – 8
= x(x – 4) + 2(x – 4)
= (x - 4)(x + 2)
Therefore, x = 4, -2.
= x(x – 4) + 2(x – 4)
= (x - 4)(x + 2)
Therefore, x = 4, -2.
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –- a)x2 – 2x – 4
- b)4x2 – 2x + 1
- c)2x2 + 4x – 1
- d)2x2 – 4x – 1
Correct answer is option 'D'. Can you explain this answer?
If 2 and (- 1/2) as the sum and product of its zeros respectively then the quadratic polynomial f(x) is –
a)
x2 – 2x – 4
b)
4x2 – 2x + 1
c)
2x2 + 4x – 1
d)
2x2 – 4x – 1
|
|
Archana gupta answered |
Understanding Quadratic Polynomials
A quadratic polynomial can be expressed in the form f(x) = ax² + bx + c, where the zeros (roots) of the polynomial can be derived from its coefficients.
Given Conditions
- Sum of Zeros (α + β): 2
- Product of Zeros (αβ): -1/2
Using the Relationships
For a quadratic polynomial f(x) = ax² + bx + c:
- The sum of the zeros is given by -b/a.
- The product of the zeros is given by c/a.
Using the conditions:
1. Sum of Zeros:
- -b/a = 2
- Therefore, b = -2a
2. Product of Zeros:
- c/a = -1/2
- Therefore, c = -a/2
Forming the Polynomial
Substituting b and c into the polynomial form:
f(x) = ax² + (-2a)x + (-a/2)
To eliminate the fraction, multiply through by 2:
f(x) = 2ax² - 4ax - a
Assuming a = 1 for simplicity:
f(x) = 2x² - 4x - 1
Thus, the polynomial becomes:
Final Polynomial
- f(x) = 2x² - 4x - 1
This corresponds to option D.
Conclusion
The correct quadratic polynomial based on the provided sum and product of its zeros is:
- 2x² - 4x - 1 (Option D)
A quadratic polynomial can be expressed in the form f(x) = ax² + bx + c, where the zeros (roots) of the polynomial can be derived from its coefficients.
Given Conditions
- Sum of Zeros (α + β): 2
- Product of Zeros (αβ): -1/2
Using the Relationships
For a quadratic polynomial f(x) = ax² + bx + c:
- The sum of the zeros is given by -b/a.
- The product of the zeros is given by c/a.
Using the conditions:
1. Sum of Zeros:
- -b/a = 2
- Therefore, b = -2a
2. Product of Zeros:
- c/a = -1/2
- Therefore, c = -a/2
Forming the Polynomial
Substituting b and c into the polynomial form:
f(x) = ax² + (-2a)x + (-a/2)
To eliminate the fraction, multiply through by 2:
f(x) = 2ax² - 4ax - a
Assuming a = 1 for simplicity:
f(x) = 2x² - 4x - 1
Thus, the polynomial becomes:
Final Polynomial
- f(x) = 2x² - 4x - 1
This corresponds to option D.
Conclusion
The correct quadratic polynomial based on the provided sum and product of its zeros is:
- 2x² - 4x - 1 (Option D)
If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 – 4x + 9 is 3, then its third zero is- a)9/2
- b)-3/2
- c)3/2
- d)-9/2
Correct answer is option 'B'. Can you explain this answer?
If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 – 4x + 9 is 3, then its third zero is
a)
9/2
b)
-3/2
c)
3/2
d)
-9/2
|
Nalini rane answered |
+ 4x is 2, find the third zero.
We can start by using Vieta's formulas, which state that the sum of the zeros of a polynomial is equal to -b/a and the product of the zeros is equal to c/a, where a, b, and c are the coefficients of the polynomial.
In this case, a = 2, b = 6, and c = 4, so we have:
Sum of zeros = -b/a = -6/2 = -3
Product of zeros = c/a = 4/2 = 2
Let the three zeros be r, s, and t. We know that rs = 2, so we can write:
t = 2/rs
t = 2/(rs)
t = 2/(2)
t = 1
Therefore, the third zero is 1.
We can start by using Vieta's formulas, which state that the sum of the zeros of a polynomial is equal to -b/a and the product of the zeros is equal to c/a, where a, b, and c are the coefficients of the polynomial.
In this case, a = 2, b = 6, and c = 4, so we have:
Sum of zeros = -b/a = -6/2 = -3
Product of zeros = c/a = 4/2 = 2
Let the three zeros be r, s, and t. We know that rs = 2, so we can write:
t = 2/rs
t = 2/(rs)
t = 2/(2)
t = 1
Therefore, the third zero is 1.
What is the quadratic polynomial whose sum and the product of zeroes is √2, 1/3 respectively?- a)3x2 - 3√2x +1
- b)3x2 + 3√2x +1
- c)3x2 + 3√2x -1
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
What is the quadratic polynomial whose sum and the product of zeroes is √2, 1/3 respectively?
a)
3x2 - 3√2x +1
b)
3x2 + 3√2x +1
c)
3x2 + 3√2x -1
d)
None of the above
|
Gowri Mehta answered |
Understanding the Problem
To find the quadratic polynomial based on the given sum and product of its zeroes, we can use Vieta's formulas. For a quadratic polynomial in the form of ax² + bx + c, the relationships are:
- Sum of zeroes (α + β) = -b/a
- Product of zeroes (αβ) = c/a
In this case, we have:
- Sum of zeroes = √2
- Product of zeroes = 1/3
Formulating the Polynomial
1. Using Vieta's Formulas:
- From the sum of zeroes: α + β = √2
- Hence, -b/a = √2
- From the product of zeroes: αβ = 1/3
- Hence, c/a = 1/3
2. Choosing a Value for 'a':
- Let's choose a = 3 (to eliminate fractions easily).
- Then, -b/3 = √2 implies b = -3√2.
- For c, we have c/3 = 1/3, leading to c = 1.
Constructing the Polynomial
Now substituting the values of a, b, and c into the quadratic polynomial form:
- The polynomial becomes:
3x² - 3√2x + 1
Conclusion
The required quadratic polynomial is:
3x² - 3√2x + 1
Thus, the correct answer is option 'A'.
To find the quadratic polynomial based on the given sum and product of its zeroes, we can use Vieta's formulas. For a quadratic polynomial in the form of ax² + bx + c, the relationships are:
- Sum of zeroes (α + β) = -b/a
- Product of zeroes (αβ) = c/a
In this case, we have:
- Sum of zeroes = √2
- Product of zeroes = 1/3
Formulating the Polynomial
1. Using Vieta's Formulas:
- From the sum of zeroes: α + β = √2
- Hence, -b/a = √2
- From the product of zeroes: αβ = 1/3
- Hence, c/a = 1/3
2. Choosing a Value for 'a':
- Let's choose a = 3 (to eliminate fractions easily).
- Then, -b/3 = √2 implies b = -3√2.
- For c, we have c/3 = 1/3, leading to c = 1.
Constructing the Polynomial
Now substituting the values of a, b, and c into the quadratic polynomial form:
- The polynomial becomes:
3x² - 3√2x + 1
Conclusion
The required quadratic polynomial is:
3x² - 3√2x + 1
Thus, the correct answer is option 'A'.
The zeroes of the quadratic polynomial x2 + 99x + 127 are- a)both positive
- b)both negative
- c)one positive and one negative
- d)both equal
Correct answer is option 'B'. Can you explain this answer?
The zeroes of the quadratic polynomial x2 + 99x + 127 are
a)
both positive
b)
both negative
c)
one positive and one negative
d)
both equal
|
|
EduRev Class 10 answered |
Given quadratic polynomial is x2 + 99x + 127.
By comparing with the standard form, we get;
a = 1, b = 99 and c = 127
a > 0, b > 0 and c > 0
We know that in any quadratic polynomial, if all the coefficients have the same sign, then the zeroes of that polynomial will be negative.
Therefore, the zeroes of the given quadratic polynomial are negative.
Zeroes of p(x) = x2-27 are:- a)±9√3
- b)±3√3
- c)±7√3
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Zeroes of p(x) = x2-27 are:
a)
±9√3
b)
±3√3
c)
±7√3
d)
None of the above
|
|
Kds Coaching answered |
x2 - 27 = 0
x2 = 27
x = √27
x = ±3√3
The graph of a quadratic polynomial is a parabola which cuts the X- axis at- a)four points
- b)at most three points
- c)at most two points
- d)one point only
Correct answer is option 'C'. Can you explain this answer?
The graph of a quadratic polynomial is a parabola which cuts the X- axis at
a)
four points
b)
at most three points
c)
at most two points
d)
one point only
|
Sudha patil answered |
Explanation:
Answer: Option C (at most two points)
- A quadratic polynomial is an expression in the form of ax²+bx+c, where a, b, and c are constants and a is not equal to zero.
- The graph of a quadratic polynomial is a parabola.
- A parabola is a U-shaped curve that can either be facing upwards or downwards depending on the sign of a.
- When a parabola intersects the x-axis, it means that the value of y is equal to zero at that point.
- To find the x-intercepts of a parabola, we need to set y=0 and solve for x.
- The number of x-intercepts a parabola has depends on the discriminant of the quadratic equation.
- The discriminant is the part of the quadratic formula under the square root sign, which is b²-4ac.
- If the discriminant is positive, then the quadratic equation has two real roots, which means that the parabola intersects the x-axis at two points.
- If the discriminant is zero, then the quadratic equation has one real root, which means that the parabola intersects the x-axis at one point.
- If the discriminant is negative, then the quadratic equation has no real roots, which means that the parabola does not intersect the x-axis.
- Therefore, the graph of a quadratic polynomial can intersect the x-axis at most two points.
Answer: Option C (at most two points)
If the zeroes of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal, then- a)c and b have opposite signs
- b)c and a have opposite signs
- c)c and b have same signs
- d)c and a have same signs
Correct answer is option 'D'. Can you explain this answer?
If the zeroes of the quadratic polynomial ax2 + bx + c, c ≠ 0 are equal, then
a)
c and b have opposite signs
b)
c and a have opposite signs
c)
c and b have same signs
d)
c and a have same signs
|
|
Nk Classes answered |
For equal roots, discriminant will be equal to zero.
b2 -4ac = 0
b2 = 4ac
ac = b2/4
ac > 0 (as square of any number cannot be negative)
The graph of the polynomial f(x) = 2x – 5 crosses the X-axis at the point- a)(5/2, 0)
- b)(1, -3)
- c)(0, 0)
- d)(4, 3)
Correct answer is option 'A'. Can you explain this answer?
The graph of the polynomial f(x) = 2x – 5 crosses the X-axis at the point
a)
(5/2, 0)
b)
(1, -3)
c)
(0, 0)
d)
(4, 3)
|
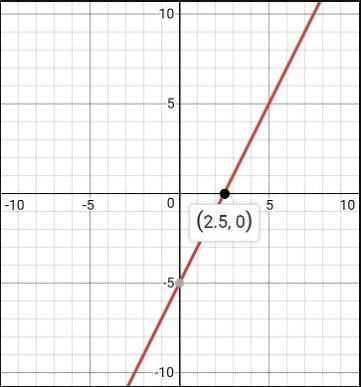
Akshay Iyer answered |
The graph of the polynomial
f (x) = 2x - 5
f (x) = 2x - 5
Method.
Let us consider, y = f (x) = 2x - 5
Now, when x = 0, y = - 5
and when y = 0, x = 5/2
So, we get two points (0, - 5) and (5/2, 0).
We plot the two points on a graph paper considering two rectangular axes XOX' and YOY'. Then, we find a straight line as shown in the graph.
We see that the line intersects x-axis at the point (5/2, 0).
Chapter doubts & questions for Polynomial Equations - Mathematics: Algebra 2 2025 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Polynomial Equations - Mathematics: Algebra 2 in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Mathematics: Algebra 2
52 videos|114 docs|37 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily