All Exams >
CLAT >
4 Months Preparation Course for CLAT UG >
All Questions
All questions of Ratio And Proportion for CLAT Exam
An amount of money is to be divided between P, Q and R in the ratio of 3:7:12.If the difference between the shares of P and Q is Rs.X, and the difference between Q and R’s share is Rs.3000. Find the total amount of money?- a)11000
- b)12400
- c)13200
- d)14300
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
An amount of money is to be divided between P, Q and R in the ratio of 3:7:12.If the difference between the shares of P and Q is Rs.X, and the difference between Q and R’s share is Rs.3000. Find the total amount of money?
a)
11000
b)
12400
c)
13200
d)
14300
e)
None of these
|
Machine Experts answered |
- The shares of P, Q, and R are in the ratio of 3:7:12. Let the common factor be 'a'.
- P's share = 3a, Q's share = 7a, R's share = 12a.
- The difference between Q and R's share is 3000: 12a - 7a = 3000, which gives 5a = 3000, so a = 600.
- Now, P's difference with Q: 7a - 3a = 4a = X. Thus, X = 2400.
- Total amount = 3a + 7a + 12a = 22a = 22 * 600 = 13200.
- P's share = 3a, Q's share = 7a, R's share = 12a.
- The difference between Q and R's share is 3000: 12a - 7a = 3000, which gives 5a = 3000, so a = 600.
- Now, P's difference with Q: 7a - 3a = 4a = X. Thus, X = 2400.
- Total amount = 3a + 7a + 12a = 22a = 22 * 600 = 13200.
If 4a = 5 b and 7b = 9c then a : b : c = ?- a)45 : 36 : 28
- b)44 : 33 : 28
- c)28 : 36 : 45
- d)36 : 28 : 45
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If 4a = 5 b and 7b = 9c then a : b : c = ?
a)
45 : 36 : 28
b)
44 : 33 : 28
c)
28 : 36 : 45
d)
36 : 28 : 45
e)
None of these
|
|
Nishita Dabas answered |
Given that 4a = 5b
∴ a/b = 5/4
Also 7b = 9c
∴ b/c = 9/7
∴ a : b = 5 : 4 = (5 x 9) : (4 x 9) = 45 : 36
and b : c = 9 : 7 = (9 x 4) : (7 x 4) = 36 : 28
∴ a : b : c = 45 : 36 : 28
∴ a/b = 5/4
Also 7b = 9c
∴ b/c = 9/7
∴ a : b = 5 : 4 = (5 x 9) : (4 x 9) = 45 : 36
and b : c = 9 : 7 = (9 x 4) : (7 x 4) = 36 : 28
∴ a : b : c = 45 : 36 : 28
a : b = c : d = e : f = 1 : 2 then (3a + 5c + 7e) : (3b + 5d + 7f) = ?- a)1 : 2
- b)2 : 1
- c)3 : 1
- d)1 : 3
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
a : b = c : d = e : f = 1 : 2 then (3a + 5c + 7e) : (3b + 5d + 7f) = ?
a)
1 : 2
b)
2 : 1
c)
3 : 1
d)
1 : 3
e)
None of these
|
|
Nishtha Pandey answered |
A/b=c/d=e/f=1/2
b=2a
d=2c
f=2e
then,
=3a+5c+7e/[3(2a)+5(2c)+7(2e)]
=3a+5c+7e/6a+10c+14e
=3a+5c+7e/2(3a+5c+7e)
=1/2.
The ratio between the present ages of Punit and suresh is 4 : 5. After 7 years Punit’s age will be 31 years. What was Suresh’s age four years ago- a)24 yr
- b)28 yr
- c)14 yr
- d)30 yr
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The ratio between the present ages of Punit and suresh is 4 : 5. After 7 years Punit’s age will be 31 years. What was Suresh’s age four years ago
a)
24 yr
b)
28 yr
c)
14 yr
d)
30 yr
e)
None of these
|
Eshaan Kapoor answered |
Let the present ages of Punit and Suresh be 4x and 5x
According to the question-
4x+7=31
4x=31-7
4x=24
X=6
Now, present age of suresh= 5x ⇒ 5(6)
30 years
According to the question-
4x+7=31
4x=31-7
4x=24
X=6
Now, present age of suresh= 5x ⇒ 5(6)
30 years
so, his age 4 years ago=30-4=26 years
A sum of 12600 is to be distributed between A, B and C. For every rupee A gets, B gets 80p and for every rupee B gets, C get 90 paise. Find the amount get by C.- a)3200
- b)3600
- c)4200
- d)4600
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A sum of 12600 is to be distributed between A, B and C. For every rupee A gets, B gets 80p and for every rupee B gets, C get 90 paise. Find the amount get by C.
a)
3200
b)
3600
c)
4200
d)
4600
e)
None of these
|
Preeti Khanna answered |
Ratio of money between A and B – 100:80 and that of B and C – 100:90
so the ratio between A : B :C – 100:80:72
so 252x = 12600, x = 50. So C get = 50*72 = 3600
so the ratio between A : B :C – 100:80:72
so 252x = 12600, x = 50. So C get = 50*72 = 3600
What number has to be added to each term of 3 : 5 to make the ratio 5 : 6?- a)5
- b)8
- c)6
- d)7
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
What number has to be added to each term of 3 : 5 to make the ratio 5 : 6?
a)
5
b)
8
c)
6
d)
7
e)
None of these
|
Faizan Khan answered |
The correct option is D.
Let the no be x
Implies
3+x/5+x=5/6
Implies 6(3+x)=5(5+x)
18+6x=25+5x
6x-5x=25-18
Implies x=7
7 should be added
Proof-
3+7/5+7=10/12=5/6
Let the no be x
Implies
3+x/5+x=5/6
Implies 6(3+x)=5(5+x)
18+6x=25+5x
6x-5x=25-18
Implies x=7
7 should be added
Proof-
3+7/5+7=10/12=5/6
When 40% percent of a number is added to another number the second number increases to its 20%. What is the ratio between the first and second number?- a)2:1
- b)1:2
- c)2:3
- d)3:4
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When 40% percent of a number is added to another number the second number increases to its 20%. What is the ratio between the first and second number?
a)
2:1
b)
1:2
c)
2:3
d)
3:4
e)
None of these
|
Naroj Boda answered |
Answer – b) 1:2
Explanation :
(40/100)*a + b = (120/100)*b
a:b = 1:2
Explanation :
(40/100)*a + b = (120/100)*b
a:b = 1:2
The average age of a person and his son is 30 years. The ratio of their age is 4 : 1 respectively. Find the age of son.- a)12 yr
- b)14 yr
- c)16 yr
- d)24 yr
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The average age of a person and his son is 30 years. The ratio of their age is 4 : 1 respectively. Find the age of son.
a)
12 yr
b)
14 yr
c)
16 yr
d)
24 yr
e)
None of these
|
Sajal Bdw answered |
Let ,father's age=Y years
and,son's age=X years
Acc. to question, there average is 30
therefore,
=>(X+Y)/2=30
=>X+Y=60
=>X+4X=60 (RATIO IS 4:1)
=>5X=60
=>X=12
Therefore correct answer is A
and,son's age=X years
Acc. to question, there average is 30
therefore,
=>(X+Y)/2=30
=>X+Y=60
=>X+4X=60 (RATIO IS 4:1)
=>5X=60
=>X=12
Therefore correct answer is A
A bag contains 25p coins, 50p coins and 1 rupee coins whose values are in the ratio of 8:4:2.If the total values of coins isX and the total amount in rupees is Y,thenwhich of the following is true- a)X = 840; Y = 260
- b)X = 966; Y = 345
- c)X = 840; Y = 280
- d)X = 740; Y = 260
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A bag contains 25p coins, 50p coins and 1 rupee coins whose values are in the ratio of 8:4:2.If the total values of coins isX and the total amount in rupees is Y,thenwhich of the following is true
a)
X = 840; Y = 260
b)
X = 966; Y = 345
c)
X = 840; Y = 280
d)
X = 740; Y = 260
e)
None of these
|
|
Preeti Khanna answered |
Answer – C.X = 840; Y = 280 Explanation : Value is given in the ratio 8:4:2. (8x/0.25) + (4x/0.5) + (2x/1) = 840.
X = 20. Total amount, Y = 14*20 = 280
X = 20. Total amount, Y = 14*20 = 280
Can you explain the answer of this question below:If P : Q : = 8 : 15 and Q : R = 3 : 2, then find P : Q : R
- A:
8 : 15 : 7
- B:
7 : 15 : 8
- C:
8 : 15 : 10
- D:
10 : 15 : 8
- E:
None of these
The answer is c.
If P : Q : = 8 : 15 and Q : R = 3 : 2, then find P : Q : R
8 : 15 : 7
7 : 15 : 8
8 : 15 : 10
10 : 15 : 8
None of these
|
Ravi Singh answered |
Given that, P : Q = 8 : 15, Q : R = 3 : 2
P : Q : R = (8 x 3) : (15 x 3) : (15 x 2) = 24 : 45 : 30
∴ P : Q : R = 8 : 15 : 10
Here, consequent of first ratio should be equal to the antecedent of second ratio.
The sum of the squares between three numbers is 5000. The ratio between the first and the second number is 3:4 and that of second and third number is 4:5.Find the difference between first and the third number.- a)20
- b)30
- c)40
- d)50
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The sum of the squares between three numbers is 5000. The ratio between the first and the second number is 3:4 and that of second and third number is 4:5.Find the difference between first and the third number.
a)
20
b)
30
c)
40
d)
50
e)
None of these
|
Bank Exams India answered |
Answer – A.20 Explanation : a^2 + b^2 + c^2 = 5000 a:b:c = 3:4:5 50x^2 = 5000.
X = 10.
5x – 3x = 2*10 = 20
X = 10.
5x – 3x = 2*10 = 20
The ratio between the number of boys and girls in a school is 4:5. If the number of boys are increased by 30 % and the number of girls increased by 40 %, then what will the new ratio of boys and girls in the school.- a)13/35
- b)26/35
- c)26/41
- d)23/13
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between the number of boys and girls in a school is 4:5. If the number of boys are increased by 30 % and the number of girls increased by 40 %, then what will the new ratio of boys and girls in the school.
a)
13/35
b)
26/35
c)
26/41
d)
23/13
e)
None of these
|
|
Preeti Khanna answered |
Answer – B.26/35 Explanation : boys = 4x and girls = 5x.
Required ratio = [(130/100)*4x]/ [(140/100)*5x]
Required ratio = [(130/100)*4x]/ [(140/100)*5x]
A bag contains one rupee, 50 paisa 25 paisa coins in the Ratio of 8:9:11. If the total money in the bag is Rs. 366, find the number of 25 paisa coins.
- a)264
- b)364
- c)241
- d)245
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A bag contains one rupee, 50 paisa 25 paisa coins in the Ratio of 8:9:11. If the total money in the bag is Rs. 366, find the number of 25 paisa coins.
a)
264
b)
364
c)
241
d)
245
e)
None of these
|
Glance Learning Institute answered |
Let coins are
1 ruppe coin = 8X.
Value of 1 ruppe coin = 8X.
50 paise coins = 9X
Value of 50 paise coin = 9X/2
25 paise coins = 11X
Value of 25 paise coins = 11X/4.
Total Ruppes = 366
8X + 9X/2 + 11X/4 = 366
61X/4 = 366
61X = 1464
X = 24.
Number of 25p paise coin = 11X = 11* 24 = 264.
1 ruppe coin = 8X.
Value of 1 ruppe coin = 8X.
50 paise coins = 9X
Value of 50 paise coin = 9X/2
25 paise coins = 11X
Value of 25 paise coins = 11X/4.
Total Ruppes = 366
8X + 9X/2 + 11X/4 = 366
61X/4 = 366
61X = 1464
X = 24.
Number of 25p paise coin = 11X = 11* 24 = 264.
If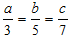 
, then find the value of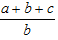 
- a)1/5
- b)1/3
- c)3
- d)5
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If 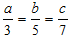, then find the value of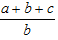
, then find the value of a)
1/5
b)
1/3
c)
3
d)
5
e)
None of these
|
Dia Mehta answered |
The correct option is C.
a/3 = b/5 = c/7 = p
a = 3p
b = 5p
c = 7p
=> a+b+c/b => 3p+5p+7p/5p => 15p/5p
=> 3/1
The answer is 3
a/3 = b/5 = c/7 = p
a = 3p
b = 5p
c = 7p
=> a+b+c/b => 3p+5p+7p/5p => 15p/5p
=> 3/1
The answer is 3
One year ago the ratio between rahul salary and rohit salary is 4:5. The ratio between their individual salary of the last year and current year is 2:3 and 3:5 respectively. If the total current salary of rahul and rohit is 4300. Then find the current salary of rahul.- a)1200
- b)1800
- c)1600
- d)2000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
One year ago the ratio between rahul salary and rohit salary is 4:5. The ratio between their individual salary of the last year and current year is 2:3 and 3:5 respectively. If the total current salary of rahul and rohit is 4300. Then find the current salary of rahul.
a)
1200
b)
1800
c)
1600
d)
2000
e)
None of these
|
|
Faizan Khan answered |
Answer – B.1800 Explanation : 4x and 5x is the last year salry of rahul and rohit respectively Rahul last year to rahul current year = 2/3 Rohit last year to rohit current year = 3/5 Current of rahul + current of rohit = 4300 (3/2)*4x + (5/3)*5x = 4300.
X = 300.
So rahul current salary = 3/2 * 4* 300 = 1800
X = 300.
So rahul current salary = 3/2 * 4* 300 = 1800
Find the mean proportional between 9 and 64.- a)25
- b)24
- c)27
- d)35
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Find the mean proportional between 9 and 64.
a)
25
b)
24
c)
27
d)
35
e)
None of these
|
Vaibhav Gupta answered |
Mean proportional is === x²=a×b
here === x²=64×9
=== so x=24 ans..
here === x²=64×9
=== so x=24 ans..
The income of riya and priya are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 2000, then find their income.- a)4000, 6000
- b)4000, 5000
- c)5000, 4000
- d)5000, 6000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The income of riya and priya are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 2000, then find their income.
a)
4000, 6000
b)
4000, 5000
c)
5000, 4000
d)
5000, 6000
e)
None of these
|
Divey Sethi answered |
Answer – b) 4000, 5000 Explanation : 4x – 2y = 2000 and 5x – 3y = 2000.
X = 1000, so income = 4000 and 5000
X = 1000, so income = 4000 and 5000
If a certain amount X is divided among A, B, C in such a way that A gets 2/3 of what B gets and B gets 1/3 of what C gets, which of the following is true- a)C’s Share = 1053 and X = 1666
- b)A’s Share = 238 and X = 1638
- c)B’s Share = 234 and X = 1666
- d)C’s Share = 1053 and X = 1638
- e)A’s Share = 351 and X = 1638
Correct answer is option 'D'. Can you explain this answer?
If a certain amount X is divided among A, B, C in such a way that A gets 2/3 of what B gets and B gets 1/3 of what C gets, which of the following is true
a)
C’s Share = 1053 and X = 1666
b)
A’s Share = 238 and X = 1638
c)
B’s Share = 234 and X = 1666
d)
C’s Share = 1053 and X = 1638
e)
A’s Share = 351 and X = 1638
|
Cstoppers Instructors answered |
A= 2/3 B; B= 1/3C;
A:B = 2:3 ; B:C = 1:3;
A:B:C = 2:3:9
C = 9/14 * 1638 = 1053
A:B = 2:3 ; B:C = 1:3;
A:B:C = 2:3:9
C = 9/14 * 1638 = 1053
Seats for Mathematics, Science and arts in a school are in the ratio 5:7:8. There is a proposal to increase these seats by X%, Y% and Z% respectively. And the ratio of increased seats is 2:3:4, which of the following is true?- a)X = 50; Z = 40
- b)Y = 40; Z = 50
- c)X = 40; Z = 75
- d)Y = 50; X = 75
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Seats for Mathematics, Science and arts in a school are in the ratio 5:7:8. There is a proposal to increase these seats by X%, Y% and Z% respectively. And the ratio of increased seats is 2:3:4, which of the following is true?
a)
X = 50; Z = 40
b)
Y = 40; Z = 50
c)
X = 40; Z = 75
d)
Y = 50; X = 75
e)
None of these
|
Aditya Kumar answered |
Number of increased seats are (140% of 5x), (150% of 7x) and (175% of 8x)
i.e., (140/100 * 5x), (150/100 * 7x) and (175/100 * 8x)
i.e., 7x, 21x/2 and 14x
Required ratio = 7x:21x/2:14x
= 14x : 21x : 28x = 2:3:4
A vessel contains milk and water in the ratio of 4:3. If 14 litres of the mixture is drawn and filled with water, the ratio changes to 3:4. How much milk was there in the vessel initially?- a)24
- b)32
- c)40
- d)48
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A vessel contains milk and water in the ratio of 4:3. If 14 litres of the mixture is drawn and filled with water, the ratio changes to 3:4. How much milk was there in the vessel initially?
a)
24
b)
32
c)
40
d)
48
e)
None of these
|
|
Cstoppers Instructors answered |
- Answer – b) 32
- Explanation :
- milk = 4x and water = 3x
- milk = 4x – 14*4/7 and water = 3x – 14*3/7 + 14
- 4x – 8: 3x + 8 = 3:4
- X = 8,
- so milk = 8*4 = 32 litres
A 50 litre of mixture contains milk and water in the ratio 2:3. How much milk must be added to the mixture so that it contains milk and water in the proportion of 3:2.- a)20
- b)25
- c)30
- d)35
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A 50 litre of mixture contains milk and water in the ratio 2:3. How much milk must be added to the mixture so that it contains milk and water in the proportion of 3:2.
a)
20
b)
25
c)
30
d)
35
e)
None of these
|
|
Aisha Gupta answered |
Answer – b) 25 Explanation : (20 + x)/30 = 3/2
The sum of the ages of a father and his son is 100 yrs now. Five years ago their ages were in the ratio 2 : 1. Find the ratio of ages of father and son after 10 years.- a)4 : 3
- b)5 : 3
- c)3 : 5
- d)10 : 7
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the ages of a father and his son is 100 yrs now. Five years ago their ages were in the ratio 2 : 1. Find the ratio of ages of father and son after 10 years.
a)
4 : 3
b)
5 : 3
c)
3 : 5
d)
10 : 7
e)
None of these
|
Notes Wala answered |
The correct option is B.
Let present age of father - x
present age of son. - y
X + Y = 100. y = 100 - x
five years ago their ages = x -5/y-5 =2/1
- x - 5 = 2y - 10 , x - 5 = (100-x)2 - 10
x - 5 = 200 - 2x - 10 , 3x = 195 ,
x = 195/3 = 65,
y = 100 - 65 = 35
Ratio after 10 years= 65+10/35+10 = 75/45 =5/3.
Let present age of father - x
present age of son. - y
X + Y = 100. y = 100 - x
five years ago their ages = x -5/y-5 =2/1
- x - 5 = 2y - 10 , x - 5 = (100-x)2 - 10
x - 5 = 200 - 2x - 10 , 3x = 195 ,
x = 195/3 = 65,
y = 100 - 65 = 35
Ratio after 10 years= 65+10/35+10 = 75/45 =5/3.
An employer reduces the number of his employees in the ratio of 7:4 and increases their wages in the ratio 3:5. State whether his bill of total wages increases or decreases and in what ratio.- a)increases 20:21
- b)decreases 21:20
- c)increases 21:22
- d)decreases 22:21
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
An employer reduces the number of his employees in the ratio of 7:4 and increases their wages in the ratio 3:5. State whether his bill of total wages increases or decreases and in what ratio.
a)
increases 20:21
b)
decreases 21:20
c)
increases 21:22
d)
decreases 22:21
e)
None of these
|
|
Aarav Sharma answered |
Given data:
- The number of employees is reduced in the ratio 7:4.
- The wages are increased in the ratio 3:5.
Let's assume that the employer had 7x employees and was paying each employee 5y wages.
After the reduction in the number of employees, the new number of employees will be 4x. But the wages have been increased in the ratio 3:5. Therefore, the new wage will be (5y * 5)/(3) = 25y/3.
So, the total bill of wages before the reduction = 7x * 5y = 35xy
And, the total bill of wages after the reduction = 4x * (25y/3) = (100xy/3)
Now, let's simplify the two bills of wages and see how they compare:
(100/3)xy - 35xy = (65/3)xy
So, the bill of total wages has decreased by (65/3)xy.
We can write this as a ratio of the two bills of wages:
New bill : Old bill = (100/3)xy : 35xy
= 100:105
= 20:21
Therefore, the correct option is (b) decreases 21:20.
- The number of employees is reduced in the ratio 7:4.
- The wages are increased in the ratio 3:5.
Let's assume that the employer had 7x employees and was paying each employee 5y wages.
After the reduction in the number of employees, the new number of employees will be 4x. But the wages have been increased in the ratio 3:5. Therefore, the new wage will be (5y * 5)/(3) = 25y/3.
So, the total bill of wages before the reduction = 7x * 5y = 35xy
And, the total bill of wages after the reduction = 4x * (25y/3) = (100xy/3)
Now, let's simplify the two bills of wages and see how they compare:
(100/3)xy - 35xy = (65/3)xy
So, the bill of total wages has decreased by (65/3)xy.
We can write this as a ratio of the two bills of wages:
New bill : Old bill = (100/3)xy : 35xy
= 100:105
= 20:21
Therefore, the correct option is (b) decreases 21:20.
An amount of money is to be distributed among P, Q and R in the ratio of 7:4:5 respectively. If the total share of P and R is 4 times the share of Q, what is definitely Q’s share?- a)2000
- b)4000
- c)6000
- d)Data inadequate
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
An amount of money is to be distributed among P, Q and R in the ratio of 7:4:5 respectively. If the total share of P and R is 4 times the share of Q, what is definitely Q’s share?
a)
2000
b)
4000
c)
6000
d)
Data inadequate
e)
None of these
|
|
Cstoppers Instructors answered |
The given ratio is:
A : B : C = 3 : 5 : 7
Let the common factor be x. Thus, the production units will be:
A = 3x
B = 5x
C = 7x
We are also given that the total production is 30,000 units. So:
3x + 5x + 7x = 30,000
15x = 30,000
x = 2,000
Now, substitute x = 2,000 into the expressions for each product:
A's production = 3 × 2,000 = 6,000 units
B's production = 5 × 2,000 = 10,000 units
C's production = 7 × 2,000 = 14,000 units
So, the production for A, B, and C is:
A = 6,000 units
B = 10,000 units
C = 14,000 units
Final Answer:
Initial production:
A = 6,000 units, B = 10,000 units, C = 14,000 units
Initial production:
A = 6,000 units, B = 10,000 units, C = 14,000 units
The ratio of two numbers is 3:4. If 3 is subtracted from both the numbers, the ratio becomes 1:2. Find the sum of the two numbers?- a)9
- b)10.5
- c)11.5
- d)12
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio of two numbers is 3:4. If 3 is subtracted from both the numbers, the ratio becomes 1:2. Find the sum of the two numbers?
a)
9
b)
10.5
c)
11.5
d)
12
e)
None of these
|
|
Anaya Patel answered |
Answer – b) 10.5 Explanation : (3x – 3)/(4x – 3) = ½ x = 1.5 sum of the numbers = 7*1.5 = 10.5
Two numbers are in the ratio of 5:6 and if 4 is added to the first number and 4 is subtracted from the second number then the ratio becomes 3:2. Find the difference between two numbers.- a)2.5
- b)3.5
- c)4.5
- d)6.5
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Two numbers are in the ratio of 5:6 and if 4 is added to the first number and 4 is subtracted from the second number then the ratio becomes 3:2. Find the difference between two numbers.
a)
2.5
b)
3.5
c)
4.5
d)
6.5
e)
None of these
|
|
Faizan Khan answered |
Answer – a) 2.5 Explanation : (5x + 4)/ (6x -4) = 3/2
The income of Vinay and Prakash are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 5000, then find their income.- a)7500, 10000
- b)12500, 10000
- c)10000, 12500
- d)12500, 7500
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The income of Vinay and Prakash are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 5000, then find their income.
a)
7500, 10000
b)
12500, 10000
c)
10000, 12500
d)
12500, 7500
e)
None of these
|
Yash Patel answered |
4x – 2y = 5000 and 5x – 3y = 5000.
X = 2500, so income = 10000 and 12500.
X = 2500, so income = 10000 and 12500.
If the ratio of the first to second is 2:3 and that of the second to the third is 5: 8, then which of the following is true,- a)Sum = 98; A = 48
- b)Sum = 147; B = 30
- c)Sum = 147; C = 45
- d)Sum = 98; B = 30
- e)Sum = 98; C = 72
Correct answer is option 'D'. Can you explain this answer?
If the ratio of the first to second is 2:3 and that of the second to the third is 5: 8, then which of the following is true,
a)
Sum = 98; A = 48
b)
Sum = 147; B = 30
c)
Sum = 147; C = 45
d)
Sum = 98; B = 30
e)
Sum = 98; C = 72
|
|
Aarav Sharma answered |
Given ratios:
- First to second = 2:3
- Second to third = 5:8
Finding the values:
Let the first, second, and third values be 2x, 3x, and 8y respectively.
Using the first ratio:
2x/3x = 2/3
Thus, x = 3/2
Using the second ratio:
3x/8y = 5/8
Thus, y = 9/10
Finding the sum:
2x + 3x + 8y = 5x + 8y
Substituting the values of x and y:
5(3/2) + 8(9/10) = 7.5 + 7.2 = 14.7
Thus, the sum is 14.7.
Checking the options:
a) Sum = 98; A = 48
Does not match the calculated sum.
b) Sum = 147; B = 30
Does not match any of the calculated values.
c) Sum = 147; C = 45
Does not match any of the calculated values.
d) Sum = 98; B = 30
Matches the calculated value of second (3x) which is 30.
e) Sum = 98; C = 72
Does not match any of the calculated values.
Thus, option 'D' is the correct answer.
- First to second = 2:3
- Second to third = 5:8
Finding the values:
Let the first, second, and third values be 2x, 3x, and 8y respectively.
Using the first ratio:
2x/3x = 2/3
Thus, x = 3/2
Using the second ratio:
3x/8y = 5/8
Thus, y = 9/10
Finding the sum:
2x + 3x + 8y = 5x + 8y
Substituting the values of x and y:
5(3/2) + 8(9/10) = 7.5 + 7.2 = 14.7
Thus, the sum is 14.7.
Checking the options:
a) Sum = 98; A = 48
Does not match the calculated sum.
b) Sum = 147; B = 30
Does not match any of the calculated values.
c) Sum = 147; C = 45
Does not match any of the calculated values.
d) Sum = 98; B = 30
Matches the calculated value of second (3x) which is 30.
e) Sum = 98; C = 72
Does not match any of the calculated values.
Thus, option 'D' is the correct answer.
The income of Neha and Hitesh are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 2000, then find their income.- a)4000, 6000
- b)4000, 5000
- c)5000, 4000
- d)5000, 6000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The income of Neha and Hitesh are in the ratio of 4:5 and their expenditure is in the ratio of 2:3. If each of them saves 2000, then find their income.
a)
4000, 6000
b)
4000, 5000
c)
5000, 4000
d)
5000, 6000
e)
None of these
|
|
Aarav Sharma answered |
Given, the income ratio of Neha and Hitesh is 4:5 and their expenditure ratio is 2:3. Let the income of Neha and Hitesh be 4x and 5x respectively.
Savings of Neha = Income of Neha - Expenditure of Neha = 4x/2 - 2y/2 = 2x - y
Savings of Hitesh = Income of Hitesh - Expenditure of Hitesh = 5x/3 - 3y/3 = 5x/3 - y
Given, their savings are equal and is 2000 each. Therefore, we have 2x - y = 2000 and 5x/3 - y = 2000.
On solving these equations, we get x = 3000 and y = 2000.
Therefore, the income of Neha and Hitesh are 4x = 4(3000) = 12000 and 5x = 5(3000) = 15000 respectively.
Hence, the correct answer is option B) 4000, 5000.
Savings of Neha = Income of Neha - Expenditure of Neha = 4x/2 - 2y/2 = 2x - y
Savings of Hitesh = Income of Hitesh - Expenditure of Hitesh = 5x/3 - 3y/3 = 5x/3 - y
Given, their savings are equal and is 2000 each. Therefore, we have 2x - y = 2000 and 5x/3 - y = 2000.
On solving these equations, we get x = 3000 and y = 2000.
Therefore, the income of Neha and Hitesh are 4x = 4(3000) = 12000 and 5x = 5(3000) = 15000 respectively.
Hence, the correct answer is option B) 4000, 5000.
A company reduces his employee in the ratio 14 : 12 and increases their wages in the ratio 16:18, Determine whether the bill of wages increases or not and in what ratio.- a)Decreases, 28: 27
- b)Increases, 27:28
- c)Decreases, 29:28
- d)Increases, 28:29
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A company reduces his employee in the ratio 14 : 12 and increases their wages in the ratio 16:18, Determine whether the bill of wages increases or not and in what ratio.
a)
Decreases, 28: 27
b)
Increases, 27:28
c)
Decreases, 29:28
d)
Increases, 28:29
e)
None of these
|
|
Preeti Khanna answered |
Answer – a) Decreases, 28: 27 Explanation : Let initial employee be 14a and final employee be 12a similarly initial wage is 16b and final wage be 18b Total initial wage = 14a * 16b = 224ab, total final wage = 12a* 18b = 216ab So clearly wages decreases and ratio = 224ab: 216ab = 28:27
The average age of a woman and her daughter is 19 years. The ratio of their ages is 16 : 3. What is the age of the daughter? - a) 9 years
- b)3 years
- c)12 years
- d)6 years
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The average age of a woman and her daughter is 19 years. The ratio of their ages is 16 : 3. What is the age of the daughter?
a)
9 years
b)
3 years
c)
12 years
d)
6 years
e)
None of these
|
Sahil Roy answered |
Woman’s age = 16x years
Her daughter’s age = 3x years
16x + 3x = 2 × 19 = 38
19x = 38 x = 2
Daughter’s age = 3 × 2
Her daughter’s age = 3x years
If 40 percent of a number is subtracted from the second number then the second number is reduced to its 3/5. Find the ratio between the first number and the second number.- a)1:3
- b)1:2
- c)1:1
- d)2:3
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If 40 percent of a number is subtracted from the second number then the second number is reduced to its 3/5. Find the ratio between the first number and the second number.
a)
1:3
b)
1:2
c)
1:1
d)
2:3
e)
None of these
|
|
Aisha Gupta answered |
Answer – C.1:1 Explanation : [ b – (40/100)a] = (3/5)b.
So we get a = b.
So we get a = b.
In a town 80% of the population are adults of which men and women are in the ratio of 9 : 7 respectively. If the number of adult women is 4.2 Lakh, what is the total population of the town.- a)12 Lakh
- b)9.6 Lakh
- c)9.8 Lakh
- d)11.6 Lakh
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In a town 80% of the population are adults of which men and women are in the ratio of 9 : 7 respectively. If the number of adult women is 4.2 Lakh, what is the total population of the town.
a)
12 Lakh
b)
9.6 Lakh
c)
9.8 Lakh
d)
11.6 Lakh
e)
None of these
|
Hari Sankar D answered |
Let the number of adult men be N.
Then, ratio of the numbers of adult men and adult women
9 : 7 = N : 4.2
⇒ N = (9/7) x 4.2 = 5.4 Lakh
Total adult population = 4.2 + 5.4 = 9.6 lakh.
If the population of the town be M Lakh,
then, 80M/100 = 9.6
⇒ M = (9.6 x 100)/80 = 12 lakh
Then, ratio of the numbers of adult men and adult women
9 : 7 = N : 4.2
⇒ N = (9/7) x 4.2 = 5.4 Lakh
Total adult population = 4.2 + 5.4 = 9.6 lakh.
If the population of the town be M Lakh,
then, 80M/100 = 9.6
⇒ M = (9.6 x 100)/80 = 12 lakh
A bag contains 25p coins, 50p coins and 1 rupee coins whose values are in the ratio of 8:4:2. The total values of coins are 840. Then find the total number of coins- a)220
- b)240
- c)260
- d)280
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A bag contains 25p coins, 50p coins and 1 rupee coins whose values are in the ratio of 8:4:2. The total values of coins are 840. Then find the total number of coins
a)
220
b)
240
c)
260
d)
280
e)
None of these
|
Ishani Rane answered |
Value is given in the ratio 8:4:2.
(8x/0.25) + (4x/0.5) + (2x/1) = 840.
X = 20. Total amount = 14*20 = 280
A mixture contains alcohol and water in the ratio of 4 : 3. If 14 L of water is added to the mixture the ratio of Alcohol and water becomes 3 : 4, find the quantity of alcohol in the mixture.- a)35 L
- b)18 L
- c)24 L
- d)29 L
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A mixture contains alcohol and water in the ratio of 4 : 3. If 14 L of water is added to the mixture the ratio of Alcohol and water becomes 3 : 4, find the quantity of alcohol in the mixture.
a)
35 L
b)
18 L
c)
24 L
d)
29 L
e)
None of these
|
|
Aarav Sharma answered |
Given:
Initial ratio of alcohol and water = 4 : 3
After adding 14 L of water, the new ratio becomes 3 : 4
Let the initial quantity of alcohol be 4x and water be 3x
After adding 14 L of water, the quantity of water becomes 3x + 14
New ratio of alcohol and water = 3 : 4
Therefore, quantity of alcohol = 3/7 * total quantity
To find the total quantity, we can use the fact that the quantity of water has increased by 14 L.
So,
3x + 14 = 4/7 * (4x + 3x + 14)
21x + 98 = 28x + 20
7x = 78
x = 11
Therefore, initial quantity of alcohol = 4x = 44 L
Hence, the correct answer is option C.
Initial ratio of alcohol and water = 4 : 3
After adding 14 L of water, the new ratio becomes 3 : 4
Let the initial quantity of alcohol be 4x and water be 3x
After adding 14 L of water, the quantity of water becomes 3x + 14
New ratio of alcohol and water = 3 : 4
Therefore, quantity of alcohol = 3/7 * total quantity
To find the total quantity, we can use the fact that the quantity of water has increased by 14 L.
So,
3x + 14 = 4/7 * (4x + 3x + 14)
21x + 98 = 28x + 20
7x = 78
x = 11
Therefore, initial quantity of alcohol = 4x = 44 L
Hence, the correct answer is option C.
The average age of a man and his two sons, born on the same day, is 30 yr. The ratio of the ages of father to one of the sons is 5 : 2. What is the father’s age.- a)50 yr
- b)30 yr
- c)45 yr
- d)20 yr
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The average age of a man and his two sons, born on the same day, is 30 yr. The ratio of the ages of father to one of the sons is 5 : 2. What is the father’s age.
a)
50 yr
b)
30 yr
c)
45 yr
d)
20 yr
e)
None of these
|
Dhruv Mehra answered |
According to the question, average age of man and his twin sons = 30
Total age = 30 x 3 = 90 yr
According to the question, Ratio of father and one son = 5 : 2
Ratio of father and both the sons = 5 : 2 : 2(As sons are born on the same day)
5x + 2x +2x = 90 or 9x = 90
X = 10
Age of father = 5 X 10 = 50 yr.
The ratio between two numbers is 7:5. If 5 is subtracted from each of them, the new ratio becomes 3:5. Find the numbers.- a)7/2, 5/2
- b)3/2, 7/2
- c)9/2, 7/2
- d)11/2, 5/2
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The ratio between two numbers is 7:5. If 5 is subtracted from each of them, the new ratio becomes 3:5. Find the numbers.
a)
7/2, 5/2
b)
3/2, 7/2
c)
9/2, 7/2
d)
11/2, 5/2
e)
None of these
|
|
Aisha Gupta answered |
Answer – A.7/2, 5/2 Explanation : (7x – 5)/(5x – 5) = 3/5 X = 1/2 so the numbers are 7/2 and 5/2
The sum of three numbers is 980. If the ratio between first and second number is 3:4 and that of second and third is 3:7. Find the difference between first and last number.- a)380
- b)360
- c)340
- d)400
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The sum of three numbers is 980. If the ratio between first and second number is 3:4 and that of second and third is 3:7. Find the difference between first and last number.
a)
380
b)
360
c)
340
d)
400
e)
None of these
|
|
Faizan Khan answered |
Answer – a) 380 Explanation : ratio between three numbers – 9:12:28 49x = 980, x = 20 difference between number = 19*20 = 380
Two alloys contain gold and silver in the ratio of 3:7 and 7:3 respectively. In what ratio these alloys must be mixed with each other so that we get a alloy of gold and silver in the ratio of 2:3?- a)2:1
- b)3:1
- c)4:3
- d)3:5
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Two alloys contain gold and silver in the ratio of 3:7 and 7:3 respectively. In what ratio these alloys must be mixed with each other so that we get a alloy of gold and silver in the ratio of 2:3?
a)
2:1
b)
3:1
c)
4:3
d)
3:5
e)
None of these
|
|
Aarav Sharma answered |
Given:
- Two alloys with gold and silver in the ratio of 3:7 and 7:3 respectively
- Required alloy with gold and silver in the ratio of 2:3
To find:
- Ratio in which the two alloys must be mixed
Solution:
Let us assume that the first alloy has 3x amount of gold and 7x amount of silver, and the second alloy has 7y amount of gold and 3y amount of silver.
To obtain the required ratio of 2:3, we need to mix the two alloys in such a way that the resulting alloy has 2x amount of gold and 3x amount of silver.
Let us find the amount of gold and silver in the mixture:
- Gold in the mixture = 3x + 7y
- Silver in the mixture = 7x + 3y
We need to find the values of x and y such that the above equations are satisfied and the ratio of gold and silver in the mixture is 2:3.
From the given ratio of the first alloy, we have:
- (3x)/(7x) = 3/7
- x = 7/3
From the given ratio of the second alloy, we have:
- (7y)/(3y) = 7/3
- y = 3/7
Substituting the values of x and y in the equations for gold and silver in the mixture, we get:
- Gold in the mixture = 3(7/3) + 7(3/7) = 14
- Silver in the mixture = 7(7/3) + 3(3/7) = 28/3
Therefore, the ratio in which the two alloys must be mixed is:
- Gold to silver = 2:3
- Total amount of gold to total amount of silver = 14:(28/3) = 42:28 = 3:2
Hence, the correct answer is option B) 3:1.
- Two alloys with gold and silver in the ratio of 3:7 and 7:3 respectively
- Required alloy with gold and silver in the ratio of 2:3
To find:
- Ratio in which the two alloys must be mixed
Solution:
Let us assume that the first alloy has 3x amount of gold and 7x amount of silver, and the second alloy has 7y amount of gold and 3y amount of silver.
To obtain the required ratio of 2:3, we need to mix the two alloys in such a way that the resulting alloy has 2x amount of gold and 3x amount of silver.
Let us find the amount of gold and silver in the mixture:
- Gold in the mixture = 3x + 7y
- Silver in the mixture = 7x + 3y
We need to find the values of x and y such that the above equations are satisfied and the ratio of gold and silver in the mixture is 2:3.
From the given ratio of the first alloy, we have:
- (3x)/(7x) = 3/7
- x = 7/3
From the given ratio of the second alloy, we have:
- (7y)/(3y) = 7/3
- y = 3/7
Substituting the values of x and y in the equations for gold and silver in the mixture, we get:
- Gold in the mixture = 3(7/3) + 7(3/7) = 14
- Silver in the mixture = 7(7/3) + 3(3/7) = 28/3
Therefore, the ratio in which the two alloys must be mixed is:
- Gold to silver = 2:3
- Total amount of gold to total amount of silver = 14:(28/3) = 42:28 = 3:2
Hence, the correct answer is option B) 3:1.
In a school the number of boys and girls are in the ratio of 4:7. If the number of boys are increased by 25% and the number of girls are increased by 15%. What will be the new ratio of number of boys to that of girls?- a)100:131
- b)100:151
- c)100:161
- d)100:181
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a school the number of boys and girls are in the ratio of 4:7. If the number of boys are increased by 25% and the number of girls are increased by 15%. What will be the new ratio of number of boys to that of girls?
a)
100:131
b)
100:151
c)
100:161
d)
100:181
e)
None of these
|
|
Yash Patel answered |
Answer – c) 100:161 Explanation : Boys = 4x and girls = 7x Ratio = 4x*125/100 : 7x*115/100 = 100:161
Two candles of same height are lighted at the same time. The first is consumed in 6 hours and second in 4 hours. Assuming that each candles burns at a constant rate, in how many hours after being lighted, the ratio between the first and second candles becomes 2:1?- a)1 hour
- b)2 hour
- c)3 hour
- d)4 hour
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Two candles of same height are lighted at the same time. The first is consumed in 6 hours and second in 4 hours. Assuming that each candles burns at a constant rate, in how many hours after being lighted, the ratio between the first and second candles becomes 2:1?
a)
1 hour
b)
2 hour
c)
3 hour
d)
4 hour
e)
None of these
|
Nikita Singh answered |
Answer – c) 3 hour Explanation : Let height of both candles is ‘h’ and let after t times ratio between the height be 2:1 h – t*h/6 : h – t*h/4 = 2:1 t = 3
The ratio between number of girls and boys in a school is 5: 6. If 40 percent of the boys and 20 percent of the girls are scholarship holders, what percentage of the students does not get scholarship?- a)68%
- b)69%
- c)71%
- d)80%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between number of girls and boys in a school is 5: 6. If 40 percent of the boys and 20 percent of the girls are scholarship holders, what percentage of the students does not get scholarship?
a)
68%
b)
69%
c)
71%
d)
80%
e)
None of these
|
|
Alok Verma answered |
Answer – b) 69% Explanation : Girls = 5x and boys = 6x Girls that don’t get scholarship = 5x * 80/100 = 4x and boys that don’t get scholarship = 6x * 60/100 = 3.6x Percent students that didn’t get scholarship = (7.6x/11x)*100 = 69 (approx.)
Chapter doubts & questions for Ratio And Proportion - 4 Months Preparation Course for CLAT UG 2025 is part of CLAT exam preparation. The chapters have been prepared according to the CLAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CLAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ratio And Proportion - 4 Months Preparation Course for CLAT UG in English & Hindi are available as part of CLAT exam.
Download more important topics, notes, lectures and mock test series for CLAT Exam by signing up for free.
4 Months Preparation Course for CLAT UG
283 videos|1003 docs|331 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily