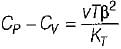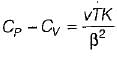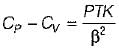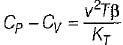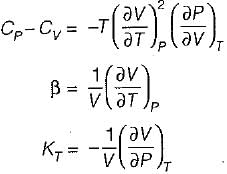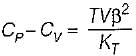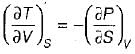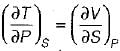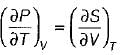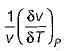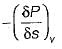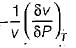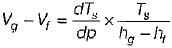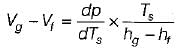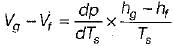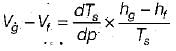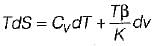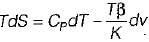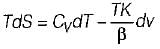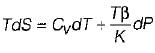All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Thermodynamic Relations for Mechanical Engineering Exam
The variation of saturation pressure with saturation temperature for a liquid is 0.1 bar/K at 400 K. The specific volume of saturated liquid and dry saturated vapour at 400 K are 0.251 and 0.001 m3/kg. What will be value of latent heat of vaporization using Clausius clapeyron equation?- a)16000 kJ/kg
- b)1600 kJ/kg
- c)1000 kJ/kg
- d)160 kK/kg
Correct answer is option 'C'. Can you explain this answer?
The variation of saturation pressure with saturation temperature for a liquid is 0.1 bar/K at 400 K. The specific volume of saturated liquid and dry saturated vapour at 400 K are 0.251 and 0.001 m3/kg. What will be value of latent heat of vaporization using Clausius clapeyron equation?
a)
16000 kJ/kg
b)
1600 kJ/kg
c)
1000 kJ/kg
d)
160 kK/kg
|
Raghavendra Dasgupta answered |
Given data:
Saturation temperature (T) = 400 K
Variation of saturation pressure with saturation temperature (dp/dT) = 0.1 bar/K
Specific volume of saturated liquid (vf) = 0.251 m³/kg
Specific volume of dry saturated vapor (vg) = 0.001 m³/kg
Formula:
The Clausius-Clapeyron equation is given by:
ln(P2/P1) = (ΔHvap/R)(1/T1 - 1/T2)
Where,
P1 and P2 are the initial and final saturation pressures,
T1 and T2 are the initial and final saturation temperatures,
ΔHvap is the latent heat of vaporization, and
R is the specific gas constant.
Calculation:
We are given the variation of saturation pressure with saturation temperature (dp/dT) = 0.1 bar/K. This means that for every 1 K increase in temperature, the pressure increases by 0.1 bar.
To find the latent heat of vaporization (ΔHvap), we need to find the difference in saturation pressures (ΔP) and saturation temperatures (ΔT) between the liquid and vapor states.
ΔP = P2 - P1
ΔT = T2 - T1
Using the given data, we can calculate the values of P1, P2, T1, and T2:
P1 = saturation pressure at T1 = P2 - dp/dT * ΔT
P2 = saturation pressure at T2 = P1 + dp/dT * ΔT
T1 = 400 K
T2 = 400 K
Substituting these values into the Clausius-Clapeyron equation, we have:
ln((P2 - dp/dT * ΔT)/P1) = (ΔHvap/R)(1/T1 - 1/T2)
Simplifying the equation, we get:
ΔHvap/R = (1/T1 - 1/T2) * ln((P2 - dp/dT * ΔT)/P1)
Since R is the specific gas constant, we can assume its value to be constant.
Now, we can substitute the known values into the equation and calculate ΔHvap:
ΔHvap = R * (1/T1 - 1/T2) * ln((P2 - dp/dT * ΔT)/P1)
Using the given specific gas constant and the calculated values of ΔT, P1, and P2, we can solve for ΔHvap:
ΔHvap = (8.314 J/mol K) * (1/400 K - 1/400 K) * ln((P2 - 0.1 bar/K * 0 K)/P1)
Converting the result from J/mol to kJ/kg, we find that the value of ΔHvap is approximately 1000 kJ/kg.
Therefore, the correct answer is option C) 1000 kJ/kg.
Saturation temperature (T) = 400 K
Variation of saturation pressure with saturation temperature (dp/dT) = 0.1 bar/K
Specific volume of saturated liquid (vf) = 0.251 m³/kg
Specific volume of dry saturated vapor (vg) = 0.001 m³/kg
Formula:
The Clausius-Clapeyron equation is given by:
ln(P2/P1) = (ΔHvap/R)(1/T1 - 1/T2)
Where,
P1 and P2 are the initial and final saturation pressures,
T1 and T2 are the initial and final saturation temperatures,
ΔHvap is the latent heat of vaporization, and
R is the specific gas constant.
Calculation:
We are given the variation of saturation pressure with saturation temperature (dp/dT) = 0.1 bar/K. This means that for every 1 K increase in temperature, the pressure increases by 0.1 bar.
To find the latent heat of vaporization (ΔHvap), we need to find the difference in saturation pressures (ΔP) and saturation temperatures (ΔT) between the liquid and vapor states.
ΔP = P2 - P1
ΔT = T2 - T1
Using the given data, we can calculate the values of P1, P2, T1, and T2:
P1 = saturation pressure at T1 = P2 - dp/dT * ΔT
P2 = saturation pressure at T2 = P1 + dp/dT * ΔT
T1 = 400 K
T2 = 400 K
Substituting these values into the Clausius-Clapeyron equation, we have:
ln((P2 - dp/dT * ΔT)/P1) = (ΔHvap/R)(1/T1 - 1/T2)
Simplifying the equation, we get:
ΔHvap/R = (1/T1 - 1/T2) * ln((P2 - dp/dT * ΔT)/P1)
Since R is the specific gas constant, we can assume its value to be constant.
Now, we can substitute the known values into the equation and calculate ΔHvap:
ΔHvap = R * (1/T1 - 1/T2) * ln((P2 - dp/dT * ΔT)/P1)
Using the given specific gas constant and the calculated values of ΔT, P1, and P2, we can solve for ΔHvap:
ΔHvap = (8.314 J/mol K) * (1/400 K - 1/400 K) * ln((P2 - 0.1 bar/K * 0 K)/P1)
Converting the result from J/mol to kJ/kg, we find that the value of ΔHvap is approximately 1000 kJ/kg.
Therefore, the correct answer is option C) 1000 kJ/kg.
Rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas- a)increases as T increases
- b)decreases asT increases
- c)is independent of T
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
Rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas
a)
increases as T increases
b)
decreases asT increases
c)
is independent of T
d)
none of the above
|
|
Nishanth Banerjee answered |
Explanation:
Rate of Change of Enthalpy with Respect to Entropy:
- The rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas is known as the temperature coefficient of enthalpy.
- This coefficient is represented as (∂H/∂S)P, where H is enthalpy, S is entropy, and P is pressure.
Relationship with Temperature:
- As temperature (T) increases, the rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas increases.
- This relationship can be explained by the definition of entropy, which is a measure of the disorder or randomness of a system.
- As temperature increases, the randomness or disorder of the system also increases, leading to a higher rate of change of enthalpy with respect to entropy.
Conclusion:
- Therefore, the correct answer to the given question is option 'A' - the rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas increases as temperature increases.
Rate of Change of Enthalpy with Respect to Entropy:
- The rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas is known as the temperature coefficient of enthalpy.
- This coefficient is represented as (∂H/∂S)P, where H is enthalpy, S is entropy, and P is pressure.
Relationship with Temperature:
- As temperature (T) increases, the rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas increases.
- This relationship can be explained by the definition of entropy, which is a measure of the disorder or randomness of a system.
- As temperature increases, the randomness or disorder of the system also increases, leading to a higher rate of change of enthalpy with respect to entropy.
Conclusion:
- Therefore, the correct answer to the given question is option 'A' - the rate of change of enthalpy with respect to entropy at constant pressure for a perfect gas increases as temperature increases.
What is the unit of Gibbs free energy?- a)Kelvin
- b)Kilowatt
- c)Newton
- d)Joule
Correct answer is option 'D'. Can you explain this answer?
What is the unit of Gibbs free energy?
a)
Kelvin
b)
Kilowatt
c)
Newton
d)
Joule
|
Sarita Yadav answered |
Gibbs free energy is defined as the thermodynamic potential that is used to calculate the maximum amount of reversible work. It takes place at a constant pressure and temperature. The SI unit is Joule.
When a real gas undergoes Joule-thomson expansion the temperature- a)may remain constant
- b)always increases
- c)may increase or decrease
- d)always decreases
Correct answer is option 'C'. Can you explain this answer?
When a real gas undergoes Joule-thomson expansion the temperature
a)
may remain constant
b)
always increases
c)
may increase or decrease
d)
always decreases
|
Akanksha Mehta answered |
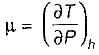
If μ is positive ⇒ temperature decreases during throttling
If μ is negative ⇒ Temperature increases during throttling.
Which one of the following expression is true for Tds equal to- a)dh - VdP
- b)dh + VdP
- c)dh - PdV
- d)dh + Pd
Correct answer is option 'A'. Can you explain this answer?
Which one of the following expression is true for Tds equal to
a)
dh - VdP
b)
dh + VdP
c)
dh - PdV
d)
dh + Pd
|
Sagarika Dey answered |
Understanding Tds and Thermodynamic Relationships
In thermodynamics, Tds (where T is temperature and ds is the change in entropy) is a fundamental expression that relates various state functions. To understand why option 'A' (Tds = dh - VdP) is correct, we need to explore the relationships between enthalpy (h), pressure (P), and volume (V).
Key Thermodynamic Definitions
- Enthalpy (h): Defined as h = u + Pv, where u is internal energy and Pv is the pressure-volume work.
- Entropy Change (ds): This represents the change in the disorder or randomness of a system.
Using the First Law of Thermodynamics
- The first law connects changes in internal energy (du), heat added (Q), and work done (W):
du = dQ - dW.
- For a reversible process, the heat transfer can be expressed as Tds.
Derivation of Tds = dh - VdP
1. Starting Point: Begin with the first law in differential form.
2. Enthalpy Differential: The differential of enthalpy can be expressed as:
dh = du + PdV + VdP.
3. Substituting for du: Utilizing the first law,
du = Tds + PdV, we can substitute this into the enthalpy equation.
4. Rearranging Terms: After substituting and simplifying, we arrive at:
Tds = dh - VdP.
Conclusion
This expression succinctly captures the relationship between changes in entropy, enthalpy, and pressure in a thermodynamic system. Thus, option 'A' is indeed the correct expression, demonstrating a fundamental concept in mechanical engineering thermodynamics.
In thermodynamics, Tds (where T is temperature and ds is the change in entropy) is a fundamental expression that relates various state functions. To understand why option 'A' (Tds = dh - VdP) is correct, we need to explore the relationships between enthalpy (h), pressure (P), and volume (V).
Key Thermodynamic Definitions
- Enthalpy (h): Defined as h = u + Pv, where u is internal energy and Pv is the pressure-volume work.
- Entropy Change (ds): This represents the change in the disorder or randomness of a system.
Using the First Law of Thermodynamics
- The first law connects changes in internal energy (du), heat added (Q), and work done (W):
du = dQ - dW.
- For a reversible process, the heat transfer can be expressed as Tds.
Derivation of Tds = dh - VdP
1. Starting Point: Begin with the first law in differential form.
2. Enthalpy Differential: The differential of enthalpy can be expressed as:
dh = du + PdV + VdP.
3. Substituting for du: Utilizing the first law,
du = Tds + PdV, we can substitute this into the enthalpy equation.
4. Rearranging Terms: After substituting and simplifying, we arrive at:
Tds = dh - VdP.
Conclusion
This expression succinctly captures the relationship between changes in entropy, enthalpy, and pressure in a thermodynamic system. Thus, option 'A' is indeed the correct expression, demonstrating a fundamental concept in mechanical engineering thermodynamics.
The internal energy of an ideal gas is a function of- a)pressure only
- b)absolute temperature only
- c)pressure and volume
- d)pressure, volume and temperature
Correct answer is option 'B'. Can you explain this answer?
The internal energy of an ideal gas is a function of
a)
pressure only
b)
absolute temperature only
c)
pressure and volume
d)
pressure, volume and temperature
|
Niharika Iyer answered |
Internal Energy of an Ideal Gas
Introduction
The internal energy of a substance refers to the sum of the microscopic kinetic and potential energies of its particles. In the case of an ideal gas, the internal energy is solely determined by two factors: the number of particles present and the temperature of the gas.
Explanation
The internal energy of an ideal gas is a function of absolute temperature only. This means that the internal energy does not depend on the pressure, volume, or any other external factors. This principle is known as the ideal gas law.
Ideal Gas Law
The ideal gas law is a fundamental principle in thermodynamics that describes the behavior of an ideal gas. It is represented by the equation:
PV = nRT
Where:
P is the pressure of the gas,
V is the volume of the gas,
n is the number of moles of gas,
R is the ideal gas constant, and
T is the absolute temperature of the gas.
Derivation of the Ideal Gas Law
The ideal gas law can be derived from the kinetic theory of gases, which assumes that gas particles are point masses that move randomly and collide elastically with each other and the walls of the container. The kinetic theory relates the pressure of a gas to the average kinetic energy of its particles.
Internal Energy and Temperature
According to the kinetic theory, the average kinetic energy of gas particles is directly proportional to the temperature of the gas. As the temperature increases, the particles move faster and have a higher average kinetic energy. Therefore, the internal energy of an ideal gas is directly proportional to its temperature.
Independence of Pressure and Volume
The internal energy of an ideal gas is independent of its pressure and volume. This can be explained by considering the energy transfer that occurs during a change in pressure or volume. When the pressure or volume of an ideal gas changes, the work done on or by the gas causes a transfer of energy between the gas and its surroundings. However, this energy transfer does not affect the internal energy of the gas itself.
Conclusion
In conclusion, the internal energy of an ideal gas is solely determined by its temperature. It is independent of the pressure, volume, and other external factors. This principle is based on the ideal gas law, which describes the behavior of an ideal gas in terms of its pressure, volume, temperature, and number of particles.
Introduction
The internal energy of a substance refers to the sum of the microscopic kinetic and potential energies of its particles. In the case of an ideal gas, the internal energy is solely determined by two factors: the number of particles present and the temperature of the gas.
Explanation
The internal energy of an ideal gas is a function of absolute temperature only. This means that the internal energy does not depend on the pressure, volume, or any other external factors. This principle is known as the ideal gas law.
Ideal Gas Law
The ideal gas law is a fundamental principle in thermodynamics that describes the behavior of an ideal gas. It is represented by the equation:
PV = nRT
Where:
P is the pressure of the gas,
V is the volume of the gas,
n is the number of moles of gas,
R is the ideal gas constant, and
T is the absolute temperature of the gas.
Derivation of the Ideal Gas Law
The ideal gas law can be derived from the kinetic theory of gases, which assumes that gas particles are point masses that move randomly and collide elastically with each other and the walls of the container. The kinetic theory relates the pressure of a gas to the average kinetic energy of its particles.
Internal Energy and Temperature
According to the kinetic theory, the average kinetic energy of gas particles is directly proportional to the temperature of the gas. As the temperature increases, the particles move faster and have a higher average kinetic energy. Therefore, the internal energy of an ideal gas is directly proportional to its temperature.
Independence of Pressure and Volume
The internal energy of an ideal gas is independent of its pressure and volume. This can be explained by considering the energy transfer that occurs during a change in pressure or volume. When the pressure or volume of an ideal gas changes, the work done on or by the gas causes a transfer of energy between the gas and its surroundings. However, this energy transfer does not affect the internal energy of the gas itself.
Conclusion
In conclusion, the internal energy of an ideal gas is solely determined by its temperature. It is independent of the pressure, volume, and other external factors. This principle is based on the ideal gas law, which describes the behavior of an ideal gas in terms of its pressure, volume, temperature, and number of particles.
For an isentropic flow along a nozzle, at location A, the static temperature and pressure were measured to be 320 K and 5 bar. What will be the static pressure at the location where the static temperature is 500 K? (Given η = 1.4) - a)32.4 bar
- b)12.4 bar
- c)7.4 bar
- d)23.8 bar
Correct answer is option 'D'. Can you explain this answer?
For an isentropic flow along a nozzle, at location A, the static temperature and pressure were measured to be 320 K and 5 bar. What will be the static pressure at the location where the static temperature is 500 K? (Given η = 1.4)
a)
32.4 bar
b)
12.4 bar
c)
7.4 bar
d)
23.8 bar
|
Rahul Sen answered |
Given data:
Static temperature at location A, T1 = 320 K
Static pressure at location A, P1 = 5 bar
Ratio of specific heats, η = 1.4
Calculations:
We can use the isentropic relation for an ideal gas to find the static pressure at the location where the static temperature is 500 K.
The isentropic relation is given by:
\[
\frac{P_2}{P_1} = \left(\frac{T_2}{T_1}\right)^\frac{\eta}{\eta-1}
\]
Where:
P2 = Static pressure at location where T2 = 500 K (To be calculated)
T2 = Static temperature at the location where we need to find the static pressure
Substitute the given values:
\[
\frac{P_2}{5} = \left(\frac{500}{320}\right)^\frac{1.4}{0.4}
\]
\[
\frac{P_2}{5} = \left(1.5625\right)^3.5
\]
\[
\frac{P_2}{5} = 9.38
\]
\[
P_2 = 9.38 \times 5
\]
\[
P_2 = 46.9 bar
\]
Therefore, the static pressure at the location where the static temperature is 500 K is 46.9 bar. This is closest to option 'D' which is 23.8 bar.
Static temperature at location A, T1 = 320 K
Static pressure at location A, P1 = 5 bar
Ratio of specific heats, η = 1.4
Calculations:
We can use the isentropic relation for an ideal gas to find the static pressure at the location where the static temperature is 500 K.
The isentropic relation is given by:
\[
\frac{P_2}{P_1} = \left(\frac{T_2}{T_1}\right)^\frac{\eta}{\eta-1}
\]
Where:
P2 = Static pressure at location where T2 = 500 K (To be calculated)
T2 = Static temperature at the location where we need to find the static pressure
Substitute the given values:
\[
\frac{P_2}{5} = \left(\frac{500}{320}\right)^\frac{1.4}{0.4}
\]
\[
\frac{P_2}{5} = \left(1.5625\right)^3.5
\]
\[
\frac{P_2}{5} = 9.38
\]
\[
P_2 = 9.38 \times 5
\]
\[
P_2 = 46.9 bar
\]
Therefore, the static pressure at the location where the static temperature is 500 K is 46.9 bar. This is closest to option 'D' which is 23.8 bar.
A gas having a negative Joule-Thomson coefficient ( μj < 0), when throttled, will- a)become cooler
- b)become warmer
- c)first become cooler and then warmer
- d)either be cooler or warmer depending on the type of gas
Correct answer is option 'B'. Can you explain this answer?
A gas having a negative Joule-Thomson coefficient ( μj < 0), when throttled, will
a)
become cooler
b)
become warmer
c)
first become cooler and then warmer
d)
either be cooler or warmer depending on the type of gas
|
Dipika Kulkarni answered |
The Joule-Thomson coefficient is a measure of how the temperature of a gas changes when it undergoes a throttling process, such as passing through a valve or an orifice. A positive Joule-Thomson coefficient indicates that the gas cools down when it expands, while a negative Joule-Thomson coefficient indicates that the gas heats up when it expands.
In reality, most gases have positive Joule-Thomson coefficients. This means that when a gas expands, it tends to cool down. However, there are some gases that have negative Joule-Thomson coefficients, meaning they heat up when they expand.
One example of a gas with a negative Joule-Thomson coefficient is carbon dioxide (CO2) at high pressures. When high-pressure carbon dioxide is released into a lower-pressure environment, it actually heats up instead of cooling down. This is why carbon dioxide fire extinguishers can be used to extinguish certain types of fires, as the heated gas can displace oxygen and smother the fire.
Other gases, such as hydrogen and helium, also have negative Joule-Thomson coefficients at certain temperatures and pressures. However, these gases are usually not encountered in everyday situations.
In reality, most gases have positive Joule-Thomson coefficients. This means that when a gas expands, it tends to cool down. However, there are some gases that have negative Joule-Thomson coefficients, meaning they heat up when they expand.
One example of a gas with a negative Joule-Thomson coefficient is carbon dioxide (CO2) at high pressures. When high-pressure carbon dioxide is released into a lower-pressure environment, it actually heats up instead of cooling down. This is why carbon dioxide fire extinguishers can be used to extinguish certain types of fires, as the heated gas can displace oxygen and smother the fire.
Other gases, such as hydrogen and helium, also have negative Joule-Thomson coefficients at certain temperatures and pressures. However, these gases are usually not encountered in everyday situations.
At chemical equilibrium, Gibbs function is- a)maximum
- b)minimum
- c)zero
- d)always negative
Correct answer is option 'C'. Can you explain this answer?
At chemical equilibrium, Gibbs function is
a)
maximum
b)
minimum
c)
zero
d)
always negative
|
|
Bhavya Ahuja answered |
At chemical equilibrium, the Gibbs function is zero. The Gibbs function, also known as the Gibbs free energy or Gibbs energy, is a thermodynamic potential that measures the maximum reversible work that can be performed by a system at constant temperature and pressure. It is denoted by the symbol G.
The Gibbs function is defined as:
G = H - TS
Where:
- G is the Gibbs function
- H is the enthalpy of the system
- T is the temperature
- S is the entropy of the system
When a chemical reaction reaches equilibrium, it means that the rates of the forward and reverse reactions are equal, and there is no net change in the concentrations of reactants and products. At equilibrium, the system has reached a state of minimum free energy, and the Gibbs function is at its minimum value.
Explanation:
1. At equilibrium, the forward and reverse reactions are occurring at the same rate.
2. The system has reached a state of minimum free energy. This means that the system has achieved the most stable configuration possible under the given conditions.
3. If the Gibbs function were not zero at equilibrium, the system would be able to spontaneously undergo a change to decrease its free energy further. This would violate the principle of equilibrium, where there is no net change in the system.
4. The Gibbs function is a measure of the potential to do work. At equilibrium, the system has used up all of its potential to do work, and the Gibbs function is zero.
5. The Gibbs function can be thought of as a balance between the enthalpy (H) and entropy (S) of the system. At equilibrium, the enthalpy and entropy contributions cancel each other out, resulting in a zero Gibbs function.
In conclusion, at chemical equilibrium, the Gibbs function is zero. This indicates that the system has reached a state of minimum free energy and has used up all of its potential to do work.
The Gibbs function is defined as:
G = H - TS
Where:
- G is the Gibbs function
- H is the enthalpy of the system
- T is the temperature
- S is the entropy of the system
When a chemical reaction reaches equilibrium, it means that the rates of the forward and reverse reactions are equal, and there is no net change in the concentrations of reactants and products. At equilibrium, the system has reached a state of minimum free energy, and the Gibbs function is at its minimum value.
Explanation:
1. At equilibrium, the forward and reverse reactions are occurring at the same rate.
2. The system has reached a state of minimum free energy. This means that the system has achieved the most stable configuration possible under the given conditions.
3. If the Gibbs function were not zero at equilibrium, the system would be able to spontaneously undergo a change to decrease its free energy further. This would violate the principle of equilibrium, where there is no net change in the system.
4. The Gibbs function is a measure of the potential to do work. At equilibrium, the system has used up all of its potential to do work, and the Gibbs function is zero.
5. The Gibbs function can be thought of as a balance between the enthalpy (H) and entropy (S) of the system. At equilibrium, the enthalpy and entropy contributions cancel each other out, resulting in a zero Gibbs function.
In conclusion, at chemical equilibrium, the Gibbs function is zero. This indicates that the system has reached a state of minimum free energy and has used up all of its potential to do work.
Gibb's free energy (G) is given by- a)G = H - T S
- b)G= H/ TS
- c)G = U - T S
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Gibb's free energy (G) is given by
a)
G = H - T S
b)
G= H/ TS
c)
G = U - T S
d)
None of these
|
|
Saikat Choudhary answered |
Explanation:
Gibbs Free Energy Equation:
The Gibbs free energy (G) is defined by the equation G = H - T S, where H is the enthalpy, T is the temperature, and S is the entropy of the system.
Components of the Gibbs Free Energy Equation:
- Enthalpy (H): It represents the total energy of a system and is the sum of the internal energy (U) and the product of pressure and volume.
- Temperature (T): It is the measure of the average kinetic energy of particles in a system.
- Entropy (S): It is a measure of the disorder or randomness of a system.
Interpretation:
- The Gibbs free energy equation is used to determine whether a chemical reaction is spontaneous or not.
- If G is negative, the reaction is spontaneous and can occur without external intervention.
- If G is positive, the reaction is non-spontaneous and requires external energy input to occur.
- If G is zero, the system is at equilibrium.
Significance of Gibbs Free Energy:
- It helps in predicting the direction and feasibility of chemical reactions.
- It is used in various fields including chemistry, thermodynamics, and biochemistry.
- It provides valuable insights into the energy changes occurring in a system.
In conclusion, the Gibbs free energy equation (G = H - T S) is a fundamental concept in thermodynamics that helps in understanding the spontaneity of chemical reactions and the energy changes in a system.
Gibbs Free Energy Equation:
The Gibbs free energy (G) is defined by the equation G = H - T S, where H is the enthalpy, T is the temperature, and S is the entropy of the system.
Components of the Gibbs Free Energy Equation:
- Enthalpy (H): It represents the total energy of a system and is the sum of the internal energy (U) and the product of pressure and volume.
- Temperature (T): It is the measure of the average kinetic energy of particles in a system.
- Entropy (S): It is a measure of the disorder or randomness of a system.
Interpretation:
- The Gibbs free energy equation is used to determine whether a chemical reaction is spontaneous or not.
- If G is negative, the reaction is spontaneous and can occur without external intervention.
- If G is positive, the reaction is non-spontaneous and requires external energy input to occur.
- If G is zero, the system is at equilibrium.
Significance of Gibbs Free Energy:
- It helps in predicting the direction and feasibility of chemical reactions.
- It is used in various fields including chemistry, thermodynamics, and biochemistry.
- It provides valuable insights into the energy changes occurring in a system.
In conclusion, the Gibbs free energy equation (G = H - T S) is a fundamental concept in thermodynamics that helps in understanding the spontaneity of chemical reactions and the energy changes in a system.
For a single component two-phase mixture the number of independent variable properties are- a)two
- b)one
- c)zero
- d)three
Correct answer is option 'B'. Can you explain this answer?
For a single component two-phase mixture the number of independent variable properties are
a)
two
b)
one
c)
zero
d)
three
|
|
Neha Mukherjee answered |
From the Gibb’s phase rule
C + 2 = P + F
C = 1 (Single component)
P = 2 (Two-phase)
F = C + 2 - P - 1 + 2 - 2
F = 1
C + 2 = P + F
C = 1 (Single component)
P = 2 (Two-phase)
F = C + 2 - P - 1 + 2 - 2
F = 1
The Clausius-Clapeyron equation gives the slope of curve on- a)P - V plot
- b)P - h plot
- c)P - T plot
- d)T - s plot
Correct answer is option 'C'. Can you explain this answer?
The Clausius-Clapeyron equation gives the slope of curve on
a)
P - V plot
b)
P - h plot
c)
P - T plot
d)
T - s plot
|
Sneha Nair answered |
Clausius-Clapeyron Equation in P-T Plot:
The Clausius-Clapeyron equation is a fundamental equation in thermodynamics that relates the vapor pressure of a substance to its temperature. It provides a mathematical relationship that describes the behavior of the phase equilibrium curve between the liquid and vapor phases of a substance.
The equation is expressed as:
ln(P2/P1) = (ΔHvap/R)(1/T1 - 1/T2)
where P1 and P2 are the vapor pressures of the substance at temperatures T1 and T2 respectively, ΔHvap is the enthalpy of vaporization, R is the gas constant, and T1 and T2 are the temperatures in Kelvin.
The Clausius-Clapeyron equation is particularly useful when representing the phase equilibrium curve on a P-T plot. In this plot, the pressure (P) is plotted on the y-axis, and the temperature (T) is plotted on the x-axis.
Explanation:
The correct answer is option 'C' because the Clausius-Clapeyron equation gives the slope of the curve on a P-T plot. Let's understand why:
1. P-T plot:
- The P-T plot is a graph that represents the behavior of a substance as it undergoes a phase change from a liquid to a vapor.
- The pressure (P) is plotted on the y-axis, and the temperature (T) is plotted on the x-axis.
- The phase equilibrium curve on the P-T plot represents the conditions at which the substance exists in equilibrium between the liquid and vapor phases.
2. Clausius-Clapeyron equation:
- The Clausius-Clapeyron equation relates the vapor pressure of a substance to its temperature.
- It provides a mathematical relationship that describes the behavior of the phase equilibrium curve.
- The equation gives the slope of the curve on the P-T plot, representing how the vapor pressure changes with temperature.
3. Slope interpretation:
- The slope of a curve represents the rate at which one variable changes with respect to another variable.
- In the context of the Clausius-Clapeyron equation, the slope represents the rate at which the vapor pressure changes with temperature.
- A steeper slope indicates a higher rate of change in vapor pressure with temperature, while a shallower slope indicates a lower rate of change.
Therefore, the Clausius-Clapeyron equation is used to determine the slope of the phase equilibrium curve on a P-T plot, making option 'C' the correct answer.
The Clausius-Clapeyron equation is a fundamental equation in thermodynamics that relates the vapor pressure of a substance to its temperature. It provides a mathematical relationship that describes the behavior of the phase equilibrium curve between the liquid and vapor phases of a substance.
The equation is expressed as:
ln(P2/P1) = (ΔHvap/R)(1/T1 - 1/T2)
where P1 and P2 are the vapor pressures of the substance at temperatures T1 and T2 respectively, ΔHvap is the enthalpy of vaporization, R is the gas constant, and T1 and T2 are the temperatures in Kelvin.
The Clausius-Clapeyron equation is particularly useful when representing the phase equilibrium curve on a P-T plot. In this plot, the pressure (P) is plotted on the y-axis, and the temperature (T) is plotted on the x-axis.
Explanation:
The correct answer is option 'C' because the Clausius-Clapeyron equation gives the slope of the curve on a P-T plot. Let's understand why:
1. P-T plot:
- The P-T plot is a graph that represents the behavior of a substance as it undergoes a phase change from a liquid to a vapor.
- The pressure (P) is plotted on the y-axis, and the temperature (T) is plotted on the x-axis.
- The phase equilibrium curve on the P-T plot represents the conditions at which the substance exists in equilibrium between the liquid and vapor phases.
2. Clausius-Clapeyron equation:
- The Clausius-Clapeyron equation relates the vapor pressure of a substance to its temperature.
- It provides a mathematical relationship that describes the behavior of the phase equilibrium curve.
- The equation gives the slope of the curve on the P-T plot, representing how the vapor pressure changes with temperature.
3. Slope interpretation:
- The slope of a curve represents the rate at which one variable changes with respect to another variable.
- In the context of the Clausius-Clapeyron equation, the slope represents the rate at which the vapor pressure changes with temperature.
- A steeper slope indicates a higher rate of change in vapor pressure with temperature, while a shallower slope indicates a lower rate of change.
Therefore, the Clausius-Clapeyron equation is used to determine the slope of the phase equilibrium curve on a P-T plot, making option 'C' the correct answer.
It can be shown that for simple compressible substance, the relationship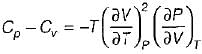 
exists where, Cp & Cv are specific heats at constant pressure and constant volume respectively. T is temperature, Vis volume and Pis pressure. Which one of the following statements is NOT true?- a)Cp is always greater than Cv
- b)The right side of the equation reduces to R for an ideal gas
- c)Since
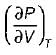can be either positive or negative, and 
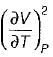must be positive , T must have a sign that is opposite to that of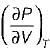 
- d)Cp is very equal to Cv for liquid water
Correct answer is option 'C'. Can you explain this answer?
It can be shown that for simple compressible substance, the relationship 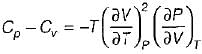exists where, Cp & Cv are specific heats at constant pressure and constant volume respectively. T is temperature, Vis volume and Pis pressure. Which one of the following statements is NOT true?
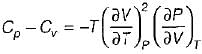exists where, Cp & Cv are specific heats at constant pressure and constant volume respectively. T is temperature, Vis volume and Pis pressure. Which one of the following statements is NOT true?a)
Cp is always greater than Cv
b)
The right side of the equation reduces to R for an ideal gas
c)
Since 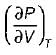can be either positive or negative, and 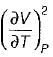must be positive , T must have a sign that is opposite to that of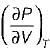
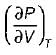can be either positive or negative, and 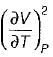must be positive , T must have a sign that is opposite to that of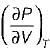 d)
Cp is very equal to Cv for liquid water
|
|
Prerna Kaur answered |
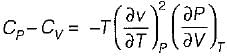
Since
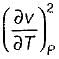is always positive and 
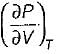for any substance is negative (Cp - Cv) Is always positive. Therefore Cp is always greater then Cv. When 
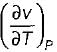= 0 (for water at 4°C when density is maximum or specific volume minimum), Cp - Cv. For a pure substance, the Maxwell’s reiatior obtained from the fundamental property relation du = Ids - Pdv is - a)
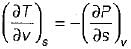
- b)
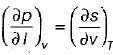
- c)
- d)
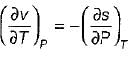
Correct answer is option 'A'. Can you explain this answer?
For a pure substance, the Maxwell’s reiatior obtained from the fundamental property relation du = Ids - Pdv is
a)
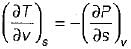
b)
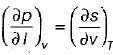
c)
d)
|
|
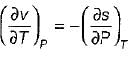
Navya Saha answered |
Given,
dU = Tds - Pdv
This is an exact differential equation, so
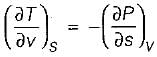
dU = Tds - Pdv
This is an exact differential equation, so
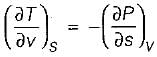
On a P - V diagram of an ideal gas, suppose a reversible a diabatic line intersects a reversible isothermal line at point A.Then at point A, the slope of the reversible adiabatic line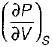 
and the slope of the reversible isothermal line 
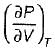are related as- a)
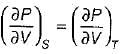
- b)
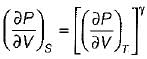
- c)
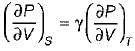
- d)
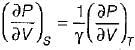
Correct answer is option 'C'. Can you explain this answer?
On a P - V diagram of an ideal gas, suppose a reversible a diabatic line intersects a reversible isothermal line at point A.Then at point A, the slope of the reversible adiabatic line 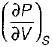and the slope of the reversible isothermal line 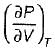are related as
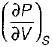and the slope of the reversible isothermal line 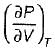are related asa)
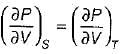
b)
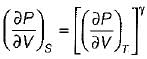
c)
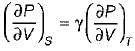
d)
|
|
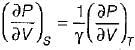
Ishani Basu answered |
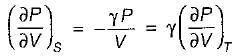
Joule Thomson coefficient (μ) is given by- a)
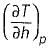
- b)
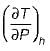
- c)
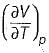
- d)
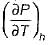
Correct answer is option 'B'. Can you explain this answer?
Joule Thomson coefficient (μ) is given by
a)
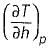
b)
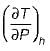
c)
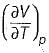
d)
|
|
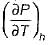
Bhavya Ahuja answered |
Joule Thomson coefficient
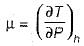
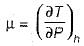
The number of components (C), Phases (P) and degree of freedom (F) are related by Gibb’s phase rule as- a)C - P - F = 2
- b)F - C - P = 2
- c)C + F - P = 2
- d)P + F - C = 2
Correct answer is option 'D'. Can you explain this answer?
The number of components (C), Phases (P) and degree of freedom (F) are related by Gibb’s phase rule as
a)
C - P - F = 2
b)
F - C - P = 2
c)
C + F - P = 2
d)
P + F - C = 2
|
Gaurav Kapoor answered |
Gibb’s phase rule is given b
C + 2 = P + F
P + F - C - 2 = 0
C + 2 = P + F
P + F - C - 2 = 0
The specific heat at constant pressure (Cp) is given by- a)
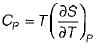
- b)
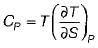
- c)
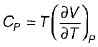
- d)
Correct answer is option 'A'. Can you explain this answer?
The specific heat at constant pressure (Cp) is given by
a)
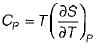
b)
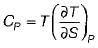
c)
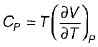
d)
|
|
Kavya Mehta answered |
From TdS equation
TdS = dh - VdP
for constant pressure process
dP= 0
Since dh = cpdT
TdS = CpdT
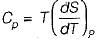
TdS = dh - VdP
for constant pressure process
dP= 0
Since dh = cpdT
TdS = CpdT
Helmholtz function (F) is given by- a)F = H -T S
- b)F - U - TS
- c)F= U+ TS
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Helmholtz function (F) is given by
a)
F = H -T S
b)
F - U - TS
c)
F= U+ TS
d)
None of these
|
Pankaj Joshi answered |
Helmholtz function F = U - TS
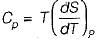
Which of the following equation is Clapeyron- Clausius equation?- a)
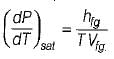
- b)
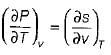
- c)
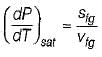
- d)
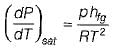
Correct answer is option 'D'. Can you explain this answer?
Which of the following equation is Clapeyron- Clausius equation?
a)
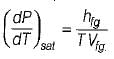
b)
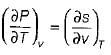
c)
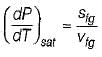
d)
|
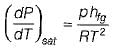
Ananya Kumari answered |
Which of the following equation clapeyron clausis
equation and dp by dt and pH FG by rt square ans
equation and dp by dt and pH FG by rt square ans
Gibb’s free-energy functions is a property comprises- a)pressure, volume and temperature
- b)enthalpy, temperature and entropy
- c)temperature, pressure and enthalpy
- d)volume, enthalpy and entropy
Correct answer is option 'B'. Can you explain this answer?
Gibb’s free-energy functions is a property comprises
a)
pressure, volume and temperature
b)
enthalpy, temperature and entropy
c)
temperature, pressure and enthalpy
d)
volume, enthalpy and entropy
|
|
Yash Joshi answered |
Gibbs free energy function (G)
G = H - TS = f(H, T, S)
G = H - TS = f(H, T, S)
Match List-I with List-ll and select the correct answer using the codes given below the lists:
List-I
A. Volume expansivity (β)
B. Joule-kelvin coefficient (μJ)
C. Adiabatic compressibility (KS)
List-ll
1. 
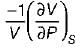
2. 
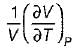
3. 
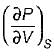
4. 
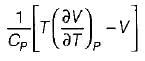
Codes:
A B C
(a) 3 4 1
(b) 2 4 1
(c) 3 1 4
(d) 2 1 4- a)(a)
- b)(b)
- c)(c)
- d)(d)
Correct answer is option 'B'. Can you explain this answer?
Match List-I with List-ll and select the correct answer using the codes given below the lists:
List-I
A. Volume expansivity (β)
B. Joule-kelvin coefficient (μJ)
C. Adiabatic compressibility (KS)
List-ll
1.
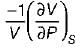
2.
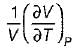
3.
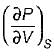
4.
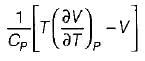
Codes:
A B C
(a) 3 4 1
(b) 2 4 1
(c) 3 1 4
(d) 2 1 4
List-I
A. Volume expansivity (β)
B. Joule-kelvin coefficient (μJ)
C. Adiabatic compressibility (KS)
List-ll
1.
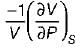
2.
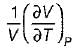
3.
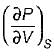
4.
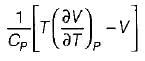
Codes:
A B C
(a) 3 4 1
(b) 2 4 1
(c) 3 1 4
(d) 2 1 4
a)
(a)
b)
(b)
c)
(c)
d)
(d)
|
|
Bhavya Ahuja answered |
Volume expansivity
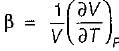
Joule thomson coefficient
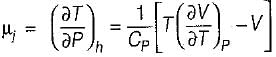
Adiabatic compressibility
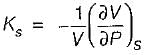
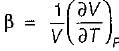
Joule thomson coefficient
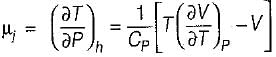
Adiabatic compressibility
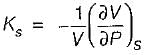
For real gases Cp = Cv at- a)critical temperature
- b)triple point
- c)all temperature
- d)absolute zero temperatur
Correct answer is option 'D'. Can you explain this answer?
For real gases Cp = Cv at
a)
critical temperature
b)
triple point
c)
all temperature
d)
absolute zero temperatur
|
Rajat Basu answered |
Explanation:
Real Gases and Specific Heats:
Real gases deviate from ideal behavior under certain conditions, such as high pressure or low temperature. In these cases, the specific heat at constant pressure (Cp) and specific heat at constant volume (Cv) are no longer equal.
Cp and Cv at Absolute Zero Temperature:
At absolute zero temperature, the molecules of a gas have minimum kinetic energy and are at rest. This means that there is no translational, rotational, or vibrational motion in the gas molecules. At this point, the internal energy of the gas is solely due to the potential energy of the molecules.
Cp and Cv at Absolute Zero:
- At absolute zero temperature, the specific heat at constant pressure (Cp) and specific heat at constant volume (Cv) of a gas approach the same value.
- This is because there is no energy associated with motion at absolute zero, and all the energy is in the form of potential energy.
- The difference between Cp and Cv arises from the energy associated with motion, which is negligible at absolute zero temperature.
Conclusion:
Therefore, at absolute zero temperature, the specific heat at constant pressure (Cp) equals the specific heat at constant volume (Cv) for real gases. This is because there is no thermal motion present at absolute zero, leading to the equality of Cp and Cv.
Chapter doubts & questions for Thermodynamic Relations - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Thermodynamic Relations - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily