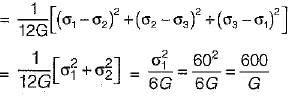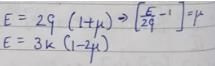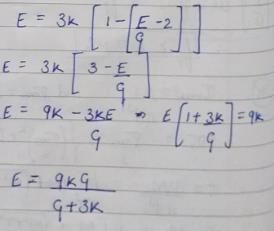All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Stress & Strain for Mechanical Engineering Exam
If the value of Poisson’s ratio is zero, then it means that
- a)The material is perfectly plastic
- b)The material is rigid
- c)There is no longitudinal strain in the material
- d)The longitudinal strain in the material is infinite
Correct answer is option 'B'. Can you explain this answer?
If the value of Poisson’s ratio is zero, then it means that
a)
The material is perfectly plastic
b)
The material is rigid
c)
There is no longitudinal strain in the material
d)
The longitudinal strain in the material is infinite
|
Pallabi Tiwari answered |
Sorry, your question is incomplete. Please provide more information or context.
If the modulus of elasticity is zero, the material is said to be- a)rigid
- b)elastic
- c)flexible
- d)plastic
Correct answer is option 'D'. Can you explain this answer?
If the modulus of elasticity is zero, the material is said to be
a)
rigid
b)
elastic
c)
flexible
d)
plastic
|
|
Prerna Menon answered |
E =0 Slope of Stress- Strain Curve is straight horizontal line. It means at constant stress, strain keeps increasing which is the characteristic property of perfectly plastic material.
A material has identical properties in all directions, it is said to be- a)homogeneous
- b)isotropic
- c)elastic
- d)orthotropic
Correct answer is option 'B'. Can you explain this answer?
A material has identical properties in all directions, it is said to be
a)
homogeneous
b)
isotropic
c)
elastic
d)
orthotropic
|
|
Divya Kulkarni answered |
Isotropic- Identical properties in all directions
Orthotropic- Different properties in all three directions
Homogeneous- A material of uniform composition
Orthotropic- Different properties in all three directions
Homogeneous- A material of uniform composition
Young’s modulus of elasticity and Poisson’s ratio of a material are 1.25 x 105 MPa and 0.34 respectively. The modulus of rigidity of the material is- a)0.4025 x105 MPa
- b)0.4664 x 105 MPa
- c)0.8375 x105 MPa
- d)0.9469 x105 MPa
Correct answer is option 'B'. Can you explain this answer?
Young’s modulus of elasticity and Poisson’s ratio of a material are 1.25 x 105 MPa and 0.34 respectively. The modulus of rigidity of the material is
a)
0.4025 x105 MPa
b)
0.4664 x 105 MPa
c)
0.8375 x105 MPa
d)
0.9469 x105 MPa
|
Sanya Agarwal answered |
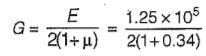= 0.4664 x 105 MPa
The principal stresses at a point in a critical - section of a machine component are σ1 = 60 MPa, σ2 = 5 MPa and σ3 = – 40 MPa. For the material of the component, the tensile yield strength is σy = 200 MPa. According to the maximum shear stress theory, the factor of safety is
- a)1.67
- b)3.6
- c)4
- d)2
Correct answer is option 'D'. Can you explain this answer?
The principal stresses at a point in a critical - section of a machine component are σ1 = 60 MPa, σ2 = 5 MPa and σ3 = – 40 MPa. For the material of the component, the tensile yield strength is σy = 200 MPa. According to the maximum shear stress theory, the factor of safety is
a)
1.67
b)
3.6
c)
4
d)
2
|
|
Pallabi Tiwari answered |
Which one of the following is correct in respect of Poisson’s ratio (v) limits for an isotropic elastic solid?
- a)- ∝ ≤ v ≤ ∝
- b)- 1 ≤ v ≤ 1/2
- c)1/4 ≤ v ≤ 1/3
- d)-1/2 ≤ v ≤ 1/2
Correct answer is option 'B'. Can you explain this answer?
Which one of the following is correct in respect of Poisson’s ratio (v) limits for an isotropic elastic solid?
a)
- ∝ ≤ v ≤ ∝
b)
- 1 ≤ v ≤ 1/2
c)
1/4 ≤ v ≤ 1/3
d)
-1/2 ≤ v ≤ 1/2
|
Bayshore Academy answered |
Isotropic Material: If the response of the material is independent of the orientation of the load axis of the sample, then we say that the material is isotropic. A material is said to be isotropic when it exhibits the same elastic properties in any direction at a given point.
The relationship between various elastic constants is:
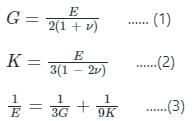
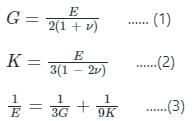
Relating the above equations, we can get the maximum and minimum values of the Poisson's ratio of an isotropic elastic solid.
In equation (1), the value of shear modulus G approaches infinity when the value of v is -1.
In equation (2), the value of bulk modulus of elasticity K approaches infinity when the value of v is 0.5.
Thus we can say that the range where Poisson's ratio vary for isotropic elastic solid is -1 ≤ v ≤ 1/2
A is sister of B. C is brother of D. If D is a sister of A, how is B related to D?- a)Brother
- b)Brother or Sister
- c)Sister
- d)Data inadequate
Correct answer is option 'B'. Can you explain this answer?
A is sister of B. C is brother of D. If D is a sister of A, how is B related to D?
a)
Brother
b)
Brother or Sister
c)
Sister
d)
Data inadequate
|
Dreamer Aarya answered |
All A, B ,C and D are brothers and sisters because as we know if B is the sister of A and even D is sister of A that means A in common is related to both B and D and they both are also related to each other as that of C.
During tensile testing of a specimen using a Universal Testing Machine, the parameters actually measured include- a)True stress and true strain
- b)Poisson’s ratio and Young’s modulus
- c)Engineering stress and engineering strain
- d)Load and deflection
Correct answer is option 'D'. Can you explain this answer?
During tensile testing of a specimen using a Universal Testing Machine, the parameters actually measured include
a)
True stress and true strain
b)
Poisson’s ratio and Young’s modulus
c)
Engineering stress and engineering strain
d)
Load and deflection
|
|
Anagha Mehta answered |
's ratio and modulus of elasticityc)Ultimate tensile strength and yield strengthd)Load and displacemente)All of the above
e) All of the above. Universal Testing Machines measure various parameters during tensile testing, including true stress and true strain, Poisson's ratio and modulus of elasticity, ultimate tensile strength and yield strength, as well as load and displacement.
e) All of the above. Universal Testing Machines measure various parameters during tensile testing, including true stress and true strain, Poisson's ratio and modulus of elasticity, ultimate tensile strength and yield strength, as well as load and displacement.
All the theories of failure, will give nearly the same result when- a)when one of the principal stresses at a point is large in comparison to the other
- b)when shear stresses act
- c)when both the principal stresses are numerically equal
- d)For all situations of stress
Correct answer is option 'A'. Can you explain this answer?
All the theories of failure, will give nearly the same result when
a)
when one of the principal stresses at a point is large in comparison to the other
b)
when shear stresses act
c)
when both the principal stresses are numerically equal
d)
For all situations of stress
|
|
Shraddha Datta answered |
When one of the principal stresses at a point is large in comparison to the other, the situation resembles uniaxial tension test. Therefore all theories give nearly the same results.
Permissible bending moment in a circular shaft under pure bending is M, according to maximum principal stress theory of failure. According to maximum shear theory of failure, the permissible bending moment in the shaft is- a)M/2
- b)M
- c)
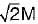
- d)2 M
Correct answer is option 'B'. Can you explain this answer?
Permissible bending moment in a circular shaft under pure bending is M, according to maximum principal stress theory of failure. According to maximum shear theory of failure, the permissible bending moment in the shaft is
a)
M/2
b)
M
c)
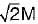
d)
2 M
|
Hiral Sharma answered |
According to maximum principal stress theory,
σ1 = σy
According to maximum shear stress theory,
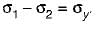
Under pure bending,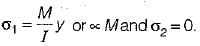
Therefore, in both the cases, permissible bending moment is M,
σ1 = σy
According to maximum shear stress theory,
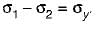
Under pure bending,
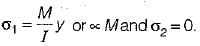
Therefore, in both the cases, permissible bending moment is M,
In a 2D stress system, the two principal stress are p1 = 180 N/mm2 (tensile) and p2 (compressive). For the materials, yield stress in simple tension and compression is 240 N/mm2 and Poisson’s ratio is 0.25. According to maximum normal strain theory for what value of p2 shall yielding commence?- a)240 N/mm2
- b)180 N/mm2
- c)195 N/mm2
- d)200 N/mm2
Correct answer is option 'C'. Can you explain this answer?
In a 2D stress system, the two principal stress are p1 = 180 N/mm2 (tensile) and p2 (compressive). For the materials, yield stress in simple tension and compression is 240 N/mm2 and Poisson’s ratio is 0.25. According to maximum normal strain theory for what value of p2 shall yielding commence?
a)
240 N/mm2
b)
180 N/mm2
c)
195 N/mm2
d)
200 N/mm2
|
|
Sankar Dasgupta answered |
Yielding may occur either in tension or compression.
For yielding in tension,
According to normal strain theory,
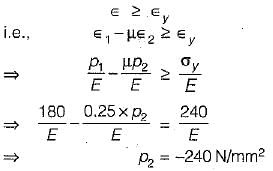
For yielding in compression,
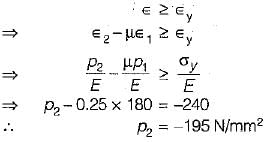
For yielding in tension,
According to normal strain theory,
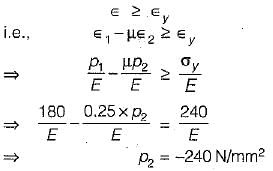
For yielding in compression,
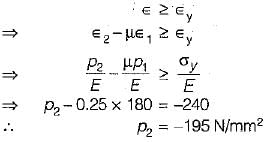
Clapeyron's theorem is associated with the analysis of- a)simply supported beams
- b)fixed beams
- c)continuous beams
- d)cantilever beams
Correct answer is option 'C'. Can you explain this answer?
Clapeyron's theorem is associated with the analysis of
a)
simply supported beams
b)
fixed beams
c)
continuous beams
d)
cantilever beams
|
|
Raghavendra Dasgupta answered |
Clapeyorn’s Theorem of Three Moments express the relation b/w bending moments at three successive supports of a continuous beam, subjected to a loading on two adjacent span with or without settlement of supports.
A cube having each side of length ‘a’ is constrained in all directions and is heated uniformly so that the temperature is raised to T°C. If α is the thermal coefficient of expansion of the cube material and E is the modulus of elasticity, the stress developed in the cube is- a)α TE/v
- b)α TE/(1-2v)
- c)α TE/2v
- d)α TE/(1 + 2v)
Correct answer is option 'B'. Can you explain this answer?
A cube having each side of length ‘a’ is constrained in all directions and is heated uniformly so that the temperature is raised to T°C. If α is the thermal coefficient of expansion of the cube material and E is the modulus of elasticity, the stress developed in the cube is
a)
α TE/v
b)
α TE/(1-2v)
c)
α TE/2v
d)
α TE/(1 + 2v)
|
|
Nilanjan Chawla answered |
For hydrostatic state stress = 0
σx = σy = σz = 0
σ = EαT/1-2μ
σx = σy = σz = 0
σ = EαT/1-2μ
A rod of length 'l’ and cross-sectional area ‘A’ rotates about an axis passing through one end of the rod. The extension produced in the rod due to centrifugal forces is (w is the weight of the rod per unit length and ω is the angular velocily of rotation of the rod)- a)
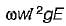
- b)
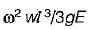
- c)
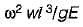
- d)
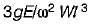
Correct answer is option 'B'. Can you explain this answer?
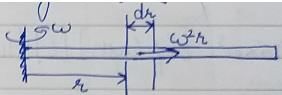
A rod of length 'l’ and cross-sectional area ‘A’ rotates about an axis passing through one end of the rod. The extension produced in the rod due to centrifugal forces is (w is the weight of the rod per unit length and ω is the angular velocily of rotation of the rod)
a)
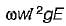
b)
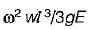
c)
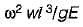
d)
|
|
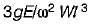
Moumita Rane answered |
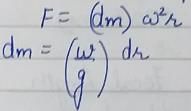
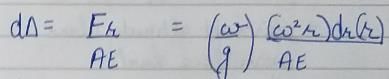
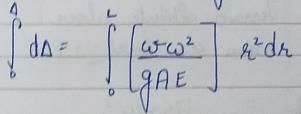
In a structural member, there are perpendicular tensile stresses of 100 N/mm2 and 50 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0.25)- a)Zero
- b)87.5 N/mm2
- c)50 N/mm2
- d)100 N/mm2
Correct answer is option 'B'. Can you explain this answer?
In a structural member, there are perpendicular tensile stresses of 100 N/mm2 and 50 N/mm2. What is the equivalent stress in simple tension, according to the maximum principal strain theory? (Poisson’s ratio = 0.25)
a)
Zero
b)
87.5 N/mm2
c)
50 N/mm2
d)
100 N/mm2
|
|
Alok Iyer answered |
Equivalent stress
= σ1 - μσ2
= 100 - 0.25 x 50 = 87.5 N/mm2
= σ1 - μσ2
= 100 - 0.25 x 50 = 87.5 N/mm2
A bar of copper and steel form a composite system. They are heated to a temperature of 40°C. What type of stress is induced in the copper bar?- a)Tensile
- b)Compressive
- c)Shear
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A bar of copper and steel form a composite system. They are heated to a temperature of 40°C. What type of stress is induced in the copper bar?
a)
Tensile
b)
Compressive
c)
Shear
d)
None of these
|
Nandita Datta answered |
°C. The coefficient of linear expansion for copper is 16.6 × 10^-6 /°C and for steel is 12 × 10^-6 /°C. Determine the change in length of the composite system if it is heated to a temperature of 100°C.
To determine the change in length of the composite system, we need to calculate the change in length for each material and then add them together.
For copper:
Coefficient of linear expansion = 16.6 × 10^-6 /°C
Initial temperature = 40°C
Final temperature = 100°C
Change in temperature = Final temperature - Initial temperature
= 100°C - 40°C
= 60°C
Change in length for copper = Coefficient of linear expansion × Initial length × Change in temperature
= 16.6 × 10^-6 /°C × Initial length × 60°C
For steel:
Coefficient of linear expansion = 12 × 10^-6 /°C
Initial temperature = 40°C
Final temperature = 100°C
Change in temperature = Final temperature - Initial temperature
= 100°C - 40°C
= 60°C
Change in length for steel = Coefficient of linear expansion × Initial length × Change in temperature
= 12 × 10^-6 /°C × Initial length × 60°C
Total change in length of the composite system = Change in length of copper + Change in length of steel
= 16.6 × 10^-6 /°C × Initial length × 60°C + 12 × 10^-6 /°C × Initial length × 60°C
Simplifying the equation:
= (16.6 + 12) × 10^-6 /°C × Initial length × 60°C
= 28.6 × 10^-6 /°C × Initial length × 60°C
Therefore, the change in length of the composite system if it is heated to a temperature of 100°C is 28.6 × 10^-6 /°C × Initial length × 60°C.
To determine the change in length of the composite system, we need to calculate the change in length for each material and then add them together.
For copper:
Coefficient of linear expansion = 16.6 × 10^-6 /°C
Initial temperature = 40°C
Final temperature = 100°C
Change in temperature = Final temperature - Initial temperature
= 100°C - 40°C
= 60°C
Change in length for copper = Coefficient of linear expansion × Initial length × Change in temperature
= 16.6 × 10^-6 /°C × Initial length × 60°C
For steel:
Coefficient of linear expansion = 12 × 10^-6 /°C
Initial temperature = 40°C
Final temperature = 100°C
Change in temperature = Final temperature - Initial temperature
= 100°C - 40°C
= 60°C
Change in length for steel = Coefficient of linear expansion × Initial length × Change in temperature
= 12 × 10^-6 /°C × Initial length × 60°C
Total change in length of the composite system = Change in length of copper + Change in length of steel
= 16.6 × 10^-6 /°C × Initial length × 60°C + 12 × 10^-6 /°C × Initial length × 60°C
Simplifying the equation:
= (16.6 + 12) × 10^-6 /°C × Initial length × 60°C
= 28.6 × 10^-6 /°C × Initial length × 60°C
Therefore, the change in length of the composite system if it is heated to a temperature of 100°C is 28.6 × 10^-6 /°C × Initial length × 60°C.
The term nominal stress in stress-strain curve for mild steel implies- a)average stress
- b)actual stress
- c)yield stress
- d)stress at necking
Correct answer is option 'A'. Can you explain this answer?
The term nominal stress in stress-strain curve for mild steel implies
a)
average stress
b)
actual stress
c)
yield stress
d)
stress at necking
|
|
Bhargavi Sarkar answered |
Actual area at instant of loading does not remain constant and decreases with increases in elongation actual stress is also called true stress.
A rod of material E = 200 x 103 MPa and α = 10-3 mm/mm/°C is fixed at both the ends. It is uniformly heated such that the increase in temperature is 30°C. The stress developed in the rod is
- a)6000 N/mm2 (tensile)
- b)6000 N/mm2 (compressive)
- c)2000 N/mm2 (tensile)
- d)2000 N/mm2 (compressive)
Correct answer is option 'B'. Can you explain this answer?
A rod of material E = 200 x 103 MPa and α = 10-3 mm/mm/°C is fixed at both the ends. It is uniformly heated such that the increase in temperature is 30°C. The stress developed in the rod is
a)
6000 N/mm2 (tensile)
b)
6000 N/mm2 (compressive)
c)
2000 N/mm2 (tensile)
d)
2000 N/mm2 (compressive)
|
|
Anuj Verma answered |
σ = E ∝ T = 200 × 103 × 10-3 × 30= 6000 N/mm2
Stress will be compressive in nature as material is not allowed to expand.
The number of independent elastic constants required to express the stress-strain relationship for linearly elastic isotropic materia! is - a)One
- b)Two
- c)Three
- d)Four
Correct answer is option 'B'. Can you explain this answer?
The number of independent elastic constants required to express the stress-strain relationship for linearly elastic isotropic materia! is
a)
One
b)
Two
c)
Three
d)
Four
|
|
Raghavendra Goyal answered |
There are two independent elastic constants E and G for an isotropic linear elastic material.
Which one of the following gives the correct expression for strain energy stored in a beam of length L and of uniform cross-section having moment of inertia I and subjected to constant bending moment M?- a)ML/EI
- b)ML/2EI
- c)M2L/EI
- d)M2L/2EI
Correct answer is option 'D'. Can you explain this answer?
Which one of the following gives the correct expression for strain energy stored in a beam of length L and of uniform cross-section having moment of inertia I and subjected to constant bending moment M?
a)
ML/EI
b)
ML/2EI
c)
M2L/EI
d)
M2L/2EI
|
Saptarshi Nair answered |
To calculate the strain energy stored in a beam under constant bending moment, we can use the formula:
Strain energy = (M^2 * L) / (2 * EI)
Where:
- M is the bending moment
- L is the length of the beam
- E is the modulus of elasticity of the material
- I is the moment of inertia of the beam's cross-section
Let's break down the formula and explain each term:
1. Bending Moment (M):
The bending moment is the internal moment that causes bending in the beam. It is a measure of the intensity of the bending load applied to the beam. In this case, the bending moment is assumed to be constant throughout the length of the beam.
2. Length of the Beam (L):
The length of the beam is simply the distance between the points where the bending moment is acting. It is an important parameter in calculating the strain energy stored in the beam.
3. Modulus of Elasticity (E):
The modulus of elasticity is a measure of the stiffness of the material. It describes how a material deforms under stress. It is a material property and is specific to each material.
4. Moment of Inertia (I):
The moment of inertia is a measure of the beam's resistance to bending. It depends on the shape and dimensions of the beam's cross-section. A beam with a higher moment of inertia will be stiffer and will store more strain energy.
5. Strain Energy:
Strain energy is the potential energy stored in a deformed material. In the case of a beam subjected to bending, the strain energy is stored in the form of internal stresses and deformations within the beam.
The formula for strain energy in a beam under constant bending moment (D) is derived from the principles of beam theory and can be derived using calculus and the concept of work done. The derivation is beyond the scope of this explanation.
In summary, the correct expression for strain energy stored in a beam of length L and uniform cross-section, subjected to constant bending moment M, is given by option D: (M^2 * L) / (2 * EI).
Strain energy = (M^2 * L) / (2 * EI)
Where:
- M is the bending moment
- L is the length of the beam
- E is the modulus of elasticity of the material
- I is the moment of inertia of the beam's cross-section
Let's break down the formula and explain each term:
1. Bending Moment (M):
The bending moment is the internal moment that causes bending in the beam. It is a measure of the intensity of the bending load applied to the beam. In this case, the bending moment is assumed to be constant throughout the length of the beam.
2. Length of the Beam (L):
The length of the beam is simply the distance between the points where the bending moment is acting. It is an important parameter in calculating the strain energy stored in the beam.
3. Modulus of Elasticity (E):
The modulus of elasticity is a measure of the stiffness of the material. It describes how a material deforms under stress. It is a material property and is specific to each material.
4. Moment of Inertia (I):
The moment of inertia is a measure of the beam's resistance to bending. It depends on the shape and dimensions of the beam's cross-section. A beam with a higher moment of inertia will be stiffer and will store more strain energy.
5. Strain Energy:
Strain energy is the potential energy stored in a deformed material. In the case of a beam subjected to bending, the strain energy is stored in the form of internal stresses and deformations within the beam.
The formula for strain energy in a beam under constant bending moment (D) is derived from the principles of beam theory and can be derived using calculus and the concept of work done. The derivation is beyond the scope of this explanation.
In summary, the correct expression for strain energy stored in a beam of length L and uniform cross-section, subjected to constant bending moment M, is given by option D: (M^2 * L) / (2 * EI).
In the case of pure bending, the beam will bend into an arc of a
- a)circle
- b)parabola
- c)ellipse
- d)hyperbola
Correct answer is option 'A'. Can you explain this answer?
In the case of pure bending, the beam will bend into an arc of a
a)
circle
b)
parabola
c)
ellipse
d)
hyperbola
|
|
Devika Tiwari answered |
In case of pure moment, bending moment at any section will be same. Thus, using double integration method to find deflection we get the equation of parabola.
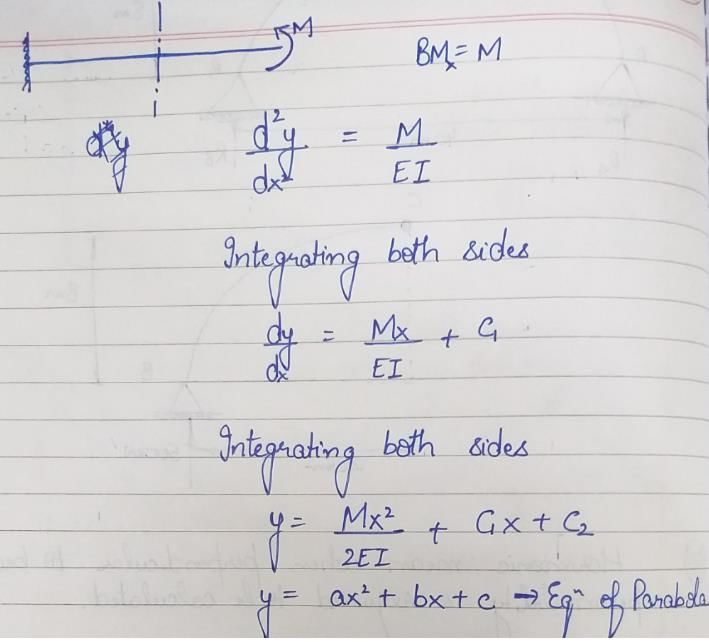
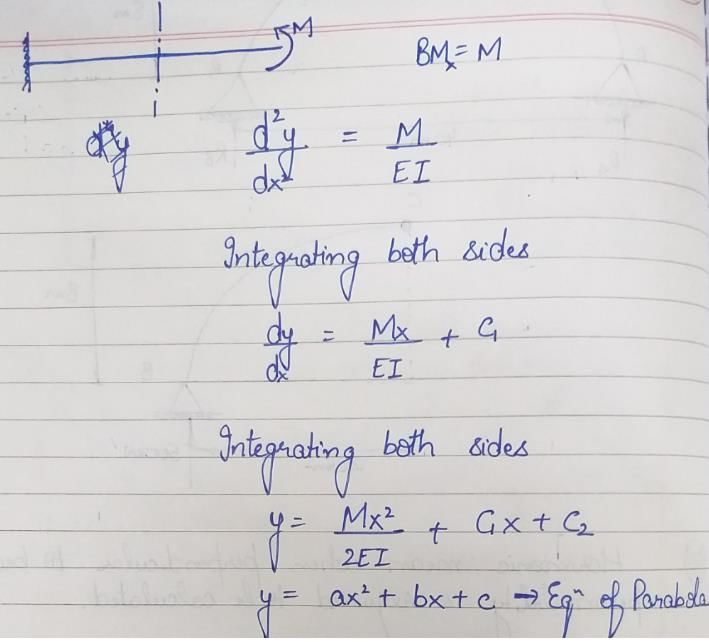
A shaft subjected to pure torsion is to be designed which of the following theories gives the largest diameter of shaft?- a)Maximum principal stress
- b)Maximum shear stress theory
- c)Strain energy theory
- d)All the above theories give same diameter
Correct answer is option 'B'. Can you explain this answer?
A shaft subjected to pure torsion is to be designed which of the following theories gives the largest diameter of shaft?
a)
Maximum principal stress
b)
Maximum shear stress theory
c)
Strain energy theory
d)
All the above theories give same diameter
|
|
Kirti Sharma answered |
It is clear from the relation T/J = (Shear Stress)/ (Radial Distance) that a shaft subjected to pure torsion is to be designed for maximum shear stress theory.
For ductile material the suitable theory of failure is- a)maximum principal stress theory
- b)maximum shear stress theory
- c)both (a) and (b)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
For ductile material the suitable theory of failure is
a)
maximum principal stress theory
b)
maximum shear stress theory
c)
both (a) and (b)
d)
None of these
|
|
Partho Jain answered |
For ductile material the most suitable theory is maximum shear stress theory.
Other theories for ductile material, Maximum Strain Energy Theory and Maximum Shear Stress Theory (Most Conservative Theory)
For brittle material the most suitable theory is Maximum Principal Stress Theory.
Other theories for brittle material, Maximum Principal Stress Theory.
Other theories for ductile material, Maximum Strain Energy Theory and Maximum Shear Stress Theory (Most Conservative Theory)
For brittle material the most suitable theory is Maximum Principal Stress Theory.
Other theories for brittle material, Maximum Principal Stress Theory.
Principle: Whoever, intending to take dishonestly any moveable property out of the possession of any person without that person's consent, moves that property in order to such taking, is said to commit theft. Explanation 1: A thing so long as it is attached to the earth, not being moveable property is not the subject of theft; but it becomes capable of being he subject of theft as soon as it is severed from the earth.Explanation 2: A moving effected by the same act which effects the severance may be a theft.Explanation 3: A person is said to cause a thing to move by removing an obstacle which prevented from moving or by separating it from any other thing, as well as by actually moving it.Explanation 4: A person, who by any means causes an animal to move, is said to move that animal, and to move everything which, in consequence of the motion so caused, is moved by that animal.Explanation 5: The consent mentioned in the definition may be express or implied and may be given either by the person in possession or by any person having for that purpose authority either express or implied.Q. Facts: A finds a ring lying on the high road, not in the possession of any person. A by taking it commits…….- a)No theft
- b)No theft though he may commit criminal misappropriation of property
- c)A Theft
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Principle: Whoever, intending to take dishonestly any moveable property out of the possession of any person without that person's consent, moves that property in order to such taking, is said to commit theft.
Explanation 1: A thing so long as it is attached to the earth, not being moveable property is not the subject of theft; but it becomes capable of being he subject of theft as soon as it is severed from the earth.
Explanation 2: A moving effected by the same act which effects the severance may be a theft.
Explanation 3: A person is said to cause a thing to move by removing an obstacle which prevented from moving or by separating it from any other thing, as well as by actually moving it.
Explanation 4: A person, who by any means causes an animal to move, is said to move that animal, and to move everything which, in consequence of the motion so caused, is moved by that animal.
Explanation 5: The consent mentioned in the definition may be express or implied and may be given either by the person in possession or by any person having for that purpose authority either express or implied.
Q.
Facts: A finds a ring lying on the high road, not in the possession of any person. A by taking it commits…….
a)
No theft
b)
No theft though he may commit criminal misappropriation of property
c)
A Theft
d)
None of the above
|
Nivedita gupta answered |
Option c is correct because that ring was out on anybody's possession if in fact it describe that ring found in any institute like temple etc where facility of counter of report available then it is theft. Principal said that theft = movable property with dishonestly intention, without possession of that person consent is theft here he had no intention hence one of important consent of theft is absent it is not theft.
Materials having elongation less than 5% are considered brittle. In such cases, factor of safety is based on- a)yield stress
- b)endurance limit
- c)limit of proportionality
- d)ultimate stress
Correct answer is option 'C'. Can you explain this answer?
Materials having elongation less than 5% are considered brittle. In such cases, factor of safety is based on
a)
yield stress
b)
endurance limit
c)
limit of proportionality
d)
ultimate stress
|
|
Neha Kumar answered |
-he limit of proportionality refers to the point beyond which Hooke's law is no longer true when stretching a material.
-When an elastic object is stretched beyond its limit of proportionality, the object does not return to its original length when the force is removed.
A free bar of length / is uniformly heated from 0°C to a temperature t°C, α is the coefficient of linear expansion and E is the modulus of elasticity. The stress in the bar is- a)α t E
- b)α t E/2
- c)zero
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A free bar of length / is uniformly heated from 0°C to a temperature t°C, α is the coefficient of linear expansion and E is the modulus of elasticity. The stress in the bar is
a)
α t E
b)
α t E/2
c)
zero
d)
None of these
|
|
Ashwin Desai answered |
Since the bar is free to expand, no stresses will be developed in the bar.
A square bar of side 40 mm and length 1 m is subjected to an axial load P. The same bar is then used as a cantilever beam and subjected to an end load P. The ratio of the strain energies, stored in the bar in the second case to that stored in the first case, is- a)16
- b)400
- c)1000
- d)2500
Correct answer is option 'D'. Can you explain this answer?
A square bar of side 40 mm and length 1 m is subjected to an axial load P. The same bar is then used as a cantilever beam and subjected to an end load P. The ratio of the strain energies, stored in the bar in the second case to that stored in the first case, is
a)
16
b)
400
c)
1000
d)
2500
|
|
Ameya Roy answered |
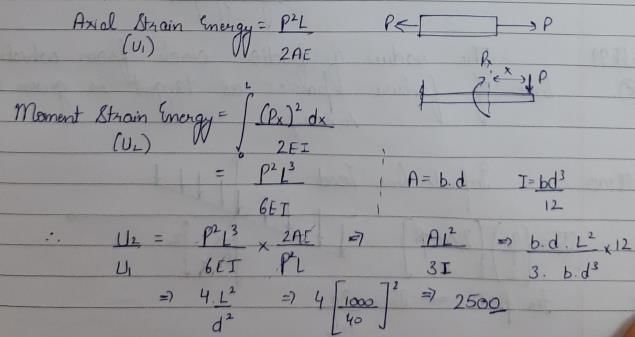
Which of the following estimates is also known as a preliminary estimate?- a)Detailed estimate
- b)Approximate estimate
- c)Scientific estimate
- d)Abstract estimate
Correct answer is option 'B'. Can you explain this answer?
Which of the following estimates is also known as a preliminary estimate?
a)
Detailed estimate
b)
Approximate estimate
c)
Scientific estimate
d)
Abstract estimate
|
Lavanya Menon answered |
An approximate estimate is prepared to decide whether the funds available for the proposal is sufficient or not. The estimate is accompanied by a detailed report explaining the necessity and utility of the proposal.
A 100 mm long and 50 mm diameter steel rod fits snugly between two rigid walls 100 mm apart at room temperature. Young's modulus of elasticity and coefficient of linear expansion of steel are 2 x 105 N/mm2 and 12 x 10-6/°C respectively. The stress developed in the rod due to a 100°C rise in temperature will be - a)6 x 10-11 N/mm2
- b)6 x 10-10 N/mm2
- c)240 N/mm2
- d)2400 N/mm2
Correct answer is option 'C'. Can you explain this answer?
A 100 mm long and 50 mm diameter steel rod fits snugly between two rigid walls 100 mm apart at room temperature. Young's modulus of elasticity and coefficient of linear expansion of steel are 2 x 105 N/mm2 and 12 x 10-6/°C respectively. The stress developed in the rod due to a 100°C rise in temperature will be
a)
6 x 10-11 N/mm2
b)
6 x 10-10 N/mm2
c)
240 N/mm2
d)
2400 N/mm2
|
|
Jay Menon answered |
l = 100 mm, d = 50 mm,
E = 2 x 105 N/mm2, α = 12 x 10-6/°C
δl = αlΔT, ε = δl/l, σ = E∈ = Eα
= 2 x 105 x 12 x 10-6 x 100 = 240 N/mm2
E = 2 x 105 N/mm2, α = 12 x 10-6/°C
δl = αlΔT, ε = δl/l, σ = E∈ = Eα
= 2 x 105 x 12 x 10-6 x 100 = 240 N/mm2
The stretch in a steel rod of circular section, having a length ℓ subjected to a tensile load P and tapering uniformly from a diameter d1, at one end to a 'diameter d2 at the other end, is given by- a)Pl/4Ed1d2
- b)Plπ/Ed1d2
- c)Pl/4E(d1-d2)
- d)4Pl/πEd1d2
Correct answer is option 'D'. Can you explain this answer?
The stretch in a steel rod of circular section, having a length ℓ subjected to a tensile load P and tapering uniformly from a diameter d1, at one end to a 'diameter d2 at the other end, is given by
a)
Pl/4Ed1d2
b)
Plπ/Ed1d2
c)
Pl/4E(d1-d2)
d)
4Pl/πEd1d2
|
|
Jay Sharma answered |
Explanation:
Given:
- Length of the steel rod = L
- Tensile load = P
- Diameter at one end = d1
- Diameter at the other end = d2
- Modulus of elasticity = E
Formula:
The stretch in a tapered steel rod can be calculated using the formula:
ΔL = 4PL / πEd1d2
Explanation of the formula:
- The formula takes into account the length of the rod (L), the applied load (P), the modulus of elasticity (E), and the diameters of the rod at each end (d1 and d2).
- The factor 4/π in the formula accounts for the tapering effect of the rod, as the diameters change from d1 to d2.
Calculation:
Substitute the given values into the formula:
ΔL = (4 * P * L) / (π * E * d1 * d2)
Thus, the correct answer is option 'D': 4PL / πEd1d2.
Given:
- Length of the steel rod = L
- Tensile load = P
- Diameter at one end = d1
- Diameter at the other end = d2
- Modulus of elasticity = E
Formula:
The stretch in a tapered steel rod can be calculated using the formula:
ΔL = 4PL / πEd1d2
Explanation of the formula:
- The formula takes into account the length of the rod (L), the applied load (P), the modulus of elasticity (E), and the diameters of the rod at each end (d1 and d2).
- The factor 4/π in the formula accounts for the tapering effect of the rod, as the diameters change from d1 to d2.
Calculation:
Substitute the given values into the formula:
ΔL = (4 * P * L) / (π * E * d1 * d2)
Thus, the correct answer is option 'D': 4PL / πEd1d2.
Notched bar tests are frequently used for testing the- a)impact strength of a material
- b)hardness of a material
- c)machinabilityofametal
- d)corrosion resistance of the material
Correct answer is option 'A'. Can you explain this answer?
Notched bar tests are frequently used for testing the
a)
impact strength of a material
b)
hardness of a material
c)
machinabilityofametal
d)
corrosion resistance of the material
|
|
Arjun Menon answered |
Notched bar tests are frequently used for testing the impact strength of a material.
The impact strength of a material refers to its ability to resist fracture under sudden loading conditions. It is an important property to consider in various engineering applications, especially those involving dynamic or impact loads. Notched bar tests are commonly employed to determine the impact strength of materials.
What are notched bar tests?
Notched bar tests involve subjecting a specimen to an impact load while having a pre-made notch or groove on the test specimen. This notch acts as a stress concentrator, creating a region of high stress concentration. By doing so, the test aims to determine the ability of the material to withstand sudden or impact loading in the presence of stress concentrations.
How are notched bar tests conducted?
The test specimen is usually in the form of a rectangular bar, which is carefully machined to have a specific shape and dimensions. The specimen is then notched, typically with a V-shape or U-shape groove, at a predetermined location. The notch geometry may vary depending on the specific testing standards or requirements.
During the test, the notched specimen is placed in a testing machine, such as a pendulum impact tester. The specimen is struck by a swinging pendulum or a falling weight, generating a sudden impact load at the notch. The energy absorbed by the specimen during fracture is measured, which provides an indication of the material's resistance to impact loading.
What does the impact strength test reveal?
The impact strength test helps to evaluate the material's ability to absorb energy and resist fracture under impact or sudden loading. It provides valuable information about the material's toughness and ductility. Materials with high impact strength can withstand sudden or dynamic loads without fracturing or experiencing catastrophic failure.
Conclusion
Notched bar tests are extensively used to assess the impact strength of materials. By introducing a stress concentration through a pre-made notch, these tests provide valuable insights into a material's ability to resist fracture under sudden or impact loading conditions. The results obtained from notched bar tests are crucial for engineers and designers to select appropriate materials for applications subjected to dynamic or impact loads.
The impact strength of a material refers to its ability to resist fracture under sudden loading conditions. It is an important property to consider in various engineering applications, especially those involving dynamic or impact loads. Notched bar tests are commonly employed to determine the impact strength of materials.
What are notched bar tests?
Notched bar tests involve subjecting a specimen to an impact load while having a pre-made notch or groove on the test specimen. This notch acts as a stress concentrator, creating a region of high stress concentration. By doing so, the test aims to determine the ability of the material to withstand sudden or impact loading in the presence of stress concentrations.
How are notched bar tests conducted?
The test specimen is usually in the form of a rectangular bar, which is carefully machined to have a specific shape and dimensions. The specimen is then notched, typically with a V-shape or U-shape groove, at a predetermined location. The notch geometry may vary depending on the specific testing standards or requirements.
During the test, the notched specimen is placed in a testing machine, such as a pendulum impact tester. The specimen is struck by a swinging pendulum or a falling weight, generating a sudden impact load at the notch. The energy absorbed by the specimen during fracture is measured, which provides an indication of the material's resistance to impact loading.
What does the impact strength test reveal?
The impact strength test helps to evaluate the material's ability to absorb energy and resist fracture under impact or sudden loading. It provides valuable information about the material's toughness and ductility. Materials with high impact strength can withstand sudden or dynamic loads without fracturing or experiencing catastrophic failure.
Conclusion
Notched bar tests are extensively used to assess the impact strength of materials. By introducing a stress concentration through a pre-made notch, these tests provide valuable insights into a material's ability to resist fracture under sudden or impact loading conditions. The results obtained from notched bar tests are crucial for engineers and designers to select appropriate materials for applications subjected to dynamic or impact loads.
The compressibility of a material is proportional to- a)Poisson’s ratio μ
- b)modulus of elasticity (E)
- c)reciprocal of μ
- d)reciprocal of E
Correct answer is option 'D'. Can you explain this answer?
The compressibility of a material is proportional to
a)
Poisson’s ratio μ
b)
modulus of elasticity (E)
c)
reciprocal of μ
d)
reciprocal of E
|
|
Snehal Tiwari answered |
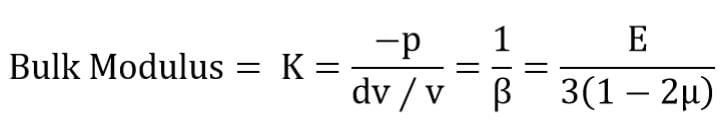
Bulk Modulus= K=(-p)/(ⅆv∕v)=1/β=E/3(1-2μ)
β=compressibility is proportional to reciprocal of E.
PRINCIPLE: (Same for question no. 11 and 12)A "contingent contract" is a contract to do or not to do something contingent on the occurrence of a particular event. Contingent contracts are permissible in law only if the events that they refer to are possible.FACT: A agrees to pay B a sum of money if B marries C. C marries D. Is this contract enforceable in law?- a)No, Contingency referred to is now impossible
- b)Yes. There is a possibility of C and D getting divorced or D dying
- c)Yes. Marriages are not permanent
- d)No. The law must assume that marriages are sacrosanct and in the eyes of law, the contingency is now impossible.
Correct answer is option 'D'. Can you explain this answer?
PRINCIPLE: (Same for question no. 11 and 12)
A "contingent contract" is a contract to do or not to do something contingent on the occurrence of a particular event. Contingent contracts are permissible in law only if the events that they refer to are possible.
FACT: A agrees to pay B a sum of money if B marries C. C marries D. Is this contract enforceable in law?
a)
No, Contingency referred to is now impossible
b)
Yes. There is a possibility of C and D getting divorced or D dying
c)
Yes. Marriages are not permanent
d)
No. The law must assume that marriages are sacrosanct and in the eyes of law, the contingency is now impossible.
|
|
Sonam joshi answered |
As per principal the Contingent contracts are permissible in law only if the events that they refer to are possible.
A certain steel has proportionality limit of 300 N/mm2 in simple tension. It is subjected to principal stress of 120 N/mm2 (tensile), 60 N/mm2 (tensile) and 30 N/mm2 (compressive). The factor of safety according to maximum shear stress theory is- a)1.50
- b)1.75
- c)1.80
- d)2.00
Correct answer is option 'D'. Can you explain this answer?
A certain steel has proportionality limit of 300 N/mm2 in simple tension. It is subjected to principal stress of 120 N/mm2 (tensile), 60 N/mm2 (tensile) and 30 N/mm2 (compressive). The factor of safety according to maximum shear stress theory is
a)
1.50
b)
1.75
c)
1.80
d)
2.00
|
|
Priyanka Shah answered |
Proportionality limit shear stress
Maximum shear stress
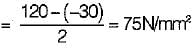
Maximum shear stress
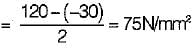
Which of the following theories of failure is most appropriate for a brittle material?- a)Maximum principal strain theory
- b)Maximum principal stress theory
- c)Maximum shear stress theory
- d)Maximum strain energy theory
Correct answer is option 'B'. Can you explain this answer?
Which of the following theories of failure is most appropriate for a brittle material?
a)
Maximum principal strain theory
b)
Maximum principal stress theory
c)
Maximum shear stress theory
d)
Maximum strain energy theory
|
|
Arshiya Roy answered |
Maximum principal stress theory (Rankine theory) is suitable for brittle materials.
In the creep test, the following type of stress is applied to the specimen- a)uniaxial compression
- b)uniaxial tension
- c)biaxial compression or tension
- d)alternating stress
Correct answer is option 'B'. Can you explain this answer?
In the creep test, the following type of stress is applied to the specimen
a)
uniaxial compression
b)
uniaxial tension
c)
biaxial compression or tension
d)
alternating stress
|
Avinash Mehta answered |
In the creep test, uniaxial tension is applied to the specimen. The purpose of the test is to measure the deformation of a material under a sustained load, which is often known as creep deformation, over a certain period of time. The test is typically used to evaluate the behavior of a material when subjected to long-term loads and it can provide information on the strength and ductility of the material, as well as its ability to maintain its properties under sustained loads. The test requires a specialized testing machine, which can apply a constant load to the specimen while monitoring the deformation over time. The results are typically presented in the form of a creep curve, which plots the deformation of the specimen over time.
For metallic minerals creep becomes an important consideration at- a)500°C
- b)550°C
- c)half of the melting point temperature on absolute scale
- d)any temperature
Correct answer is option 'C'. Can you explain this answer?
For metallic minerals creep becomes an important consideration at
a)
500°C
b)
550°C
c)
half of the melting point temperature on absolute scale
d)
any temperature
|
|
Nitya Nambiar answered |
The temperature at which the creep becomes an important consideration is called HOMOLOGOUS TEMPERATURE and this temperature is nearly half of the melting point temperature.
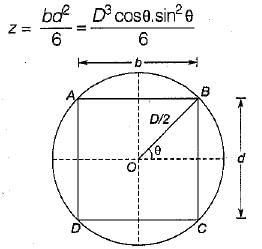
If a beam with the rectangular cross-section is obtained by cutting from circular log of timber, then for the beam to have strongest section in bending, the ratio of breadth to depth should be- a)0.500
- b)0.707
- c)0.717
- d)0.786
Correct answer is option 'B'. Can you explain this answer?
If a beam with the rectangular cross-section is obtained by cutting from circular log of timber, then for the beam to have strongest section in bending, the ratio of breadth to depth should be
a)
0.500
b)
0.707
c)
0.717
d)
0.786
|
|
Rahul Chauhan answered |
AB = b = D cosθ, BC = d = D sinθ
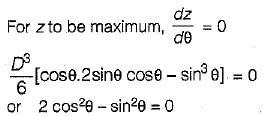
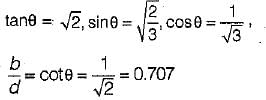
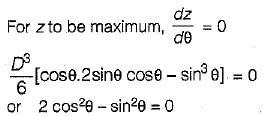
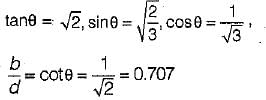
So much of the literature of the western world, including a large part of its greatest literature was either written for actual speaking or in a mode of speech. That we are likely to deform it if we apply our comparatively recent norm of writing for silent reading. It is only that so much of this work is drama or oratory (the latter including the modern forms of sermons, lectures and addresses which as late as the nineteenth century play a most important part). It is also that through classical and medieval times, and in many cases beyond these, most reading was either aloud or silently articulated as if speaking : a habit we now recognize mainly in the slang. Most classical histories were indeed quite close to oratory and public speech, rather than silent reading of an artifact, was the central condition of linguistic composition.Q. In ancient time, literature was intended to be read aloud.- a)True
- b)Untrue
- c)Insufficient information
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
So much of the literature of the western world, including a large part of its greatest literature was either written for actual speaking or in a mode of speech. That we are likely to deform it if we apply our comparatively recent norm of writing for silent reading. It is only that so much of this work is drama or oratory (the latter including the modern forms of sermons, lectures and addresses which as late as the nineteenth century play a most important part). It is also that through classical and medieval times, and in many cases beyond these, most reading was either aloud or silently articulated as if speaking : a habit we now recognize mainly in the slang. Most classical histories were indeed quite close to oratory and public speech, rather than silent reading of an artifact, was the central condition of linguistic composition.
Q.
In ancient time, literature was intended to be read aloud.
a)
True
b)
Untrue
c)
Insufficient information
d)
None of the above
|
|
Pranita kumar answered |
Literature in Ancient Times: Intended to be Read Aloud
Introduction
The question asks whether ancient literature was intended to be read aloud or not. The passage talks about the modes of speech and writing in ancient times and how they differed from our current norm of writing for silent reading.
Ancient Literature: Oratory and Drama
The passage states that a large part of the western world's greatest literature was either written for actual speaking or in a mode of speech. This includes drama and oratory, which were important forms of communication in ancient times. Oratory includes modern forms of sermons, lectures, and addresses, which played a significant role in the 19th century.
Reading Aloud: Classical and Medieval Times
The passage also mentions that most reading in classical and medieval times was either aloud or silently articulated as if speaking. This was a habit that is now recognized mainly in slang. The central condition of linguistic composition was public speech, rather than silent reading of an artifact. This means that most classical histories were quite close to oratory.
Conclusion
Based on the information provided in the passage, it can be concluded that ancient literature was indeed intended to be read aloud. The modes of speech and writing in ancient times were different from our current norm of writing for silent reading. Oratory and drama were important forms of communication, and most reading was either aloud or silently articulated as if speaking.
Introduction
The question asks whether ancient literature was intended to be read aloud or not. The passage talks about the modes of speech and writing in ancient times and how they differed from our current norm of writing for silent reading.
Ancient Literature: Oratory and Drama
The passage states that a large part of the western world's greatest literature was either written for actual speaking or in a mode of speech. This includes drama and oratory, which were important forms of communication in ancient times. Oratory includes modern forms of sermons, lectures, and addresses, which played a significant role in the 19th century.
Reading Aloud: Classical and Medieval Times
The passage also mentions that most reading in classical and medieval times was either aloud or silently articulated as if speaking. This was a habit that is now recognized mainly in slang. The central condition of linguistic composition was public speech, rather than silent reading of an artifact. This means that most classical histories were quite close to oratory.
Conclusion
Based on the information provided in the passage, it can be concluded that ancient literature was indeed intended to be read aloud. The modes of speech and writing in ancient times were different from our current norm of writing for silent reading. Oratory and drama were important forms of communication, and most reading was either aloud or silently articulated as if speaking.
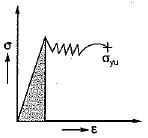
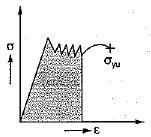
Toughness for mild steel under uniaxial tensile loading is given by the shaded portion of the stress-strain diagram as shown in- a)
- b)
- c)
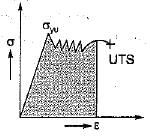
- d)
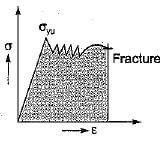
Correct answer is option 'D'. Can you explain this answer?
Toughness for mild steel under uniaxial tensile loading is given by the shaded portion of the stress-strain diagram as shown in
a)
b)
c)
d)
|
|
Nikhil Majumdar answered |
Toughness is the total area under the stress- strain curve upto fracture.
A bar of length L and of uniform cross-sectional area A. and second moment of area I is subjected to a pull P. If young’s modulus of elasticity of the bar material is E, the expression for strain energy stored in the bar will be- a)P2L/2AE
- b)PL2/2AE
- c)PL2/AE
- d)P2L/AE
Correct answer is option 'A'. Can you explain this answer?
A bar of length L and of uniform cross-sectional area A. and second moment of area I is subjected to a pull P. If young’s modulus of elasticity of the bar material is E, the expression for strain energy stored in the bar will be
a)
P2L/2AE
b)
PL2/2AE
c)
PL2/AE
d)
P2L/AE
|
Diya Chopra answered |
's modulus of the material is E, the elongation (δ) of the bar can be calculated using the following formula:
δ = PL / AE
where:
δ = elongation of the bar (m)
P = pull force applied to the bar (N)
L = length of the bar (m)
A = cross-sectional area of the bar (m^2)
E = Young's modulus of the material (Pa)
This formula assumes that the bar is linearly elastic, meaning that it will return to its original shape once the force is removed and that the force is applied along the axis of the bar. If the bar is not linearly elastic, additional factors may need to be considered.
δ = PL / AE
where:
δ = elongation of the bar (m)
P = pull force applied to the bar (N)
L = length of the bar (m)
A = cross-sectional area of the bar (m^2)
E = Young's modulus of the material (Pa)
This formula assumes that the bar is linearly elastic, meaning that it will return to its original shape once the force is removed and that the force is applied along the axis of the bar. If the bar is not linearly elastic, additional factors may need to be considered.
A tapering bar (diameters of end sections being d1 and d2) and a bar of uniform cross-section ‘d' have the same length and are subjected to the same axial pull. Both the bars will have the same extension if ‘ d ’ is equal to- a)(d1 + d2)/2
- b)
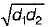
- c)
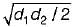
- d)
Correct answer is option 'B'. Can you explain this answer?
A tapering bar (diameters of end sections being d1 and d2) and a bar of uniform cross-section ‘d' have the same length and are subjected to the same axial pull. Both the bars will have the same extension if ‘ d ’ is equal to
a)
(d1 + d2)/2
b)
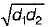
c)
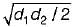
d)
|
|
Aarav Kulkarni answered |
δteper = 4Pl(πd1/d2E)
δuniform = 4Pl/(pd2 E)
∴ d =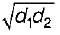
δuniform = 4Pl/(pd2 E)
∴ d =
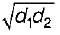
Chapter doubts & questions for Stress & Strain - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Stress & Strain - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily