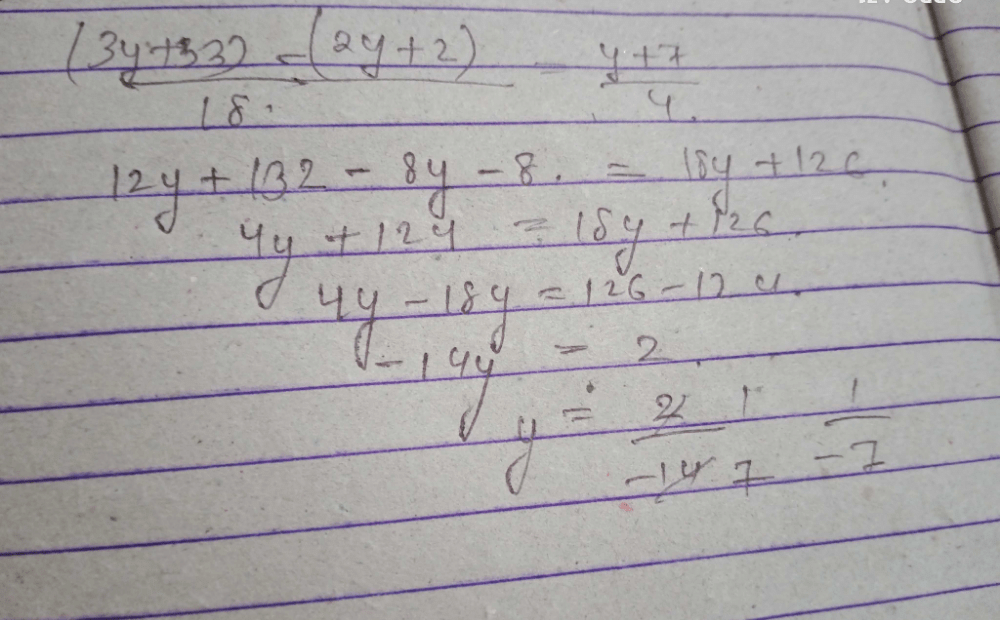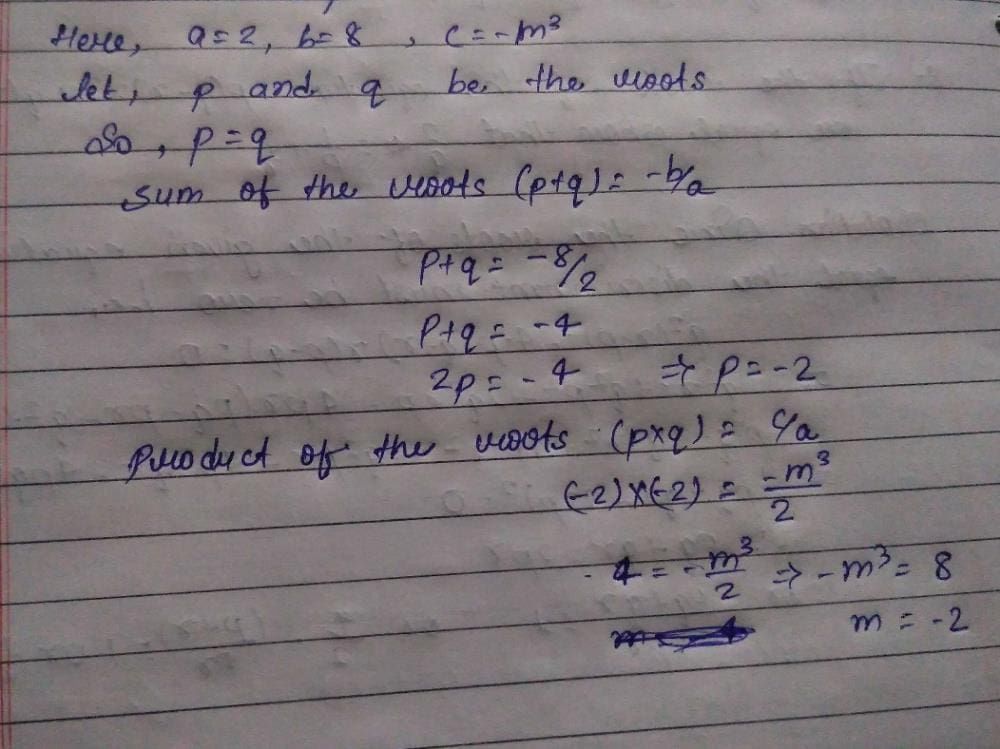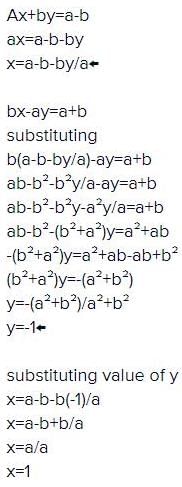All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Equations and Matrices (Old Scheme) for CA Foundation Exam
The diagonal of a rectangle is 5 cm and one of at sides is 4 cm. Its area is- a)20sq.cm.
- b)12 sq.cm.
- c)10 sq.cm.
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The diagonal of a rectangle is 5 cm and one of at sides is 4 cm. Its area is
a)
20sq.cm.
b)
12 sq.cm.
c)
10 sq.cm.
d)
none of these
|
Ishani Rane answered |
Diagonal of a rectangle divides it in two right triangles. Hence by Pythagaras theorem, the 2nd side=square root of (25-16)=3 cm. Area= 3x4 =12cm^2.
Choose the most appropriate option (a) (b) (c) or (d)
The equation –7x + 1 = 5–3x will be satisfied for x equal to:
- a)2
- b)-1
- c)1
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Choose the most appropriate option (a) (b) (c) or (d)
The equation –7x + 1 = 5–3x will be satisfied for x equal to:
a)
2
b)
-1
c)
1
d)
none of these
|
Nikita Singh answered |
Take -7x to R.H.S. and 5 to L.H.S.,
Now on R.H.S., we have -3x+7x =4x and on L.H.S., we have -5+1= -4
So the equation becomes
-4 = 4x
=> x = -1
The area of a rectangular field is 2000 sq.m and its perimeter is 180m. Form a quadratic equation by taking the length of the field as x and solve it to find the length and breadth of the field. The length and breadth are
a)(205m, 80m)b)(50m, 40m)c)(40m, 50m)d)noneCorrect answer is option 'B'. Can you explain this answer?
|
Preeti Khanna answered |
Let the length be l and the breadth be b. now area = 2000 sq.m so length * breadth = 2000; l*b=2000.
now perimeter = 180m
so 2 ( l + b ) =180;
l + b = 90;
l = 90 - b.
substituting this value of l in l * b = 2000,
( 90 - b ) * b = 2000;
90b - b^2 = 2000;
b^2 - 90b + 2000 = 0;
b^2 - 40b - 50b - 2000 = 0;
b ( b - 40 ) - 50( b - 40 ) = 0;
( b - 40 )( b - 50 ) = 0;
b = 40 or b = 50;
so l = 40 or l = 50 but the longer side is considered the length and the shorter one the breadth.
so length = 50 m and breadth = 40 m
The fourth part of a number exceeds the sixth part by 4. The number is- a)84
- b)44
- c)48
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The fourth part of a number exceeds the sixth part by 4. The number is
a)
84
b)
44
c)
48
d)
none of these
|
|
Ishani Rane answered |
Let the number be 'x'.
By the problem,
(x/4)=(x/6)+4
⇒(x/4)-(x/6)=4
⇒(3x-2x)/12=4
⇒x/12=4
⇒x=4x12
⇒x=48.
Therefore, the number is 48.
Verification:
48/4=48/6+4
12=8+4
12=12
∴LHS=RHS.
So,the number is 48.
The sum of two numbers is 52 and their difference is 2. The numbers are- a)17 and 15
- b)12 and 10
- c)27 and 25
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The sum of two numbers is 52 and their difference is 2. The numbers are
a)
17 and 15
b)
12 and 10
c)
27 and 25
d)
none of these
|
Kavita Joshi answered |
Their sum is 52, so:
52 = x + (x+2)
52 = x + x + 2
50 = x + x
50 = 2x
25 = x
So your unknown numbers x and (x+2) are 25 and 27.
Divide 56 into two parts such that three times the first part exceeds one third of the second by 48 the parts are. - a)(20,36)
- b)(25,31)
- c)(24,32)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Divide 56 into two parts such that three times the first part exceeds one third of the second by 48 the parts are.
a)
(20,36)
b)
(25,31)
c)
(24,32)
d)
none of these
|
Rajat Patel answered |
Divided 56 into two parts such that three times the first part exceed one third of second by 48.
Part one:: x
Part two:: 56-x
Equation:
3(56-x)-(1/3)x = 48
168 - 3x - (1/3)x = 48
-10/3 x = - 120
(1/3)x = 12
x = 36
56-x = 20
8 is the solution of the equation- a)
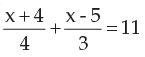
- b)
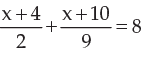
- c)
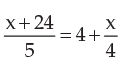
- d)
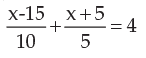
Correct answer is option 'B'. Can you explain this answer?
8 is the solution of the equation
a)
b)
c)
d)
|
Faizan Khan answered |
In option 2,
Took LCM .. SO u get 9x+36+2x+20=144.. so 11x= 88.. x=8
Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are: - a)(36, 45)
- b)(45, 36)
- c)(50, 41)
- d)(55, 46)
Correct answer is option 'B'. Can you explain this answer?
Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are:
a)
(36, 45)
b)
(45, 36)
c)
(50, 41)
d)
(55, 46)
|
Srsps answered |
Let greater number is 'x'
Smaller number be 'y
Given,greater number exceeds twice the smaller i.e 2x-2y=18...........1
1/3 of smaller and 1/5 of greater i.e 1/3×y+1/5×x=21 this is convert as 3x+5y=315......2
By solving 1 and 2 we get x=45 and y=36
Smaller number be 'y
Given,greater number exceeds twice the smaller i.e 2x-2y=18...........1
1/3 of smaller and 1/5 of greater i.e 1/3×y+1/5×x=21 this is convert as 3x+5y=315......2
By solving 1 and 2 we get x=45 and y=36
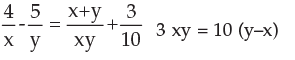
- a)(2, 5)
- b)(5, 2)
- c)(2, 7)
- d)(3, 4)
Correct answer is option 'A'. Can you explain this answer?
a)
(2, 5)
b)
(5, 2)
c)
(2, 7)
d)
(3, 4)
|
|
Faizan Khan answered |
ANSWER :- a
Solution :- 4/x - 5/y = (x+y)/ xy + 3/10
Taking L.C.M
(4y-5x)/ xy = (10x+10y+3xy) / 10xy
Cancelling both the 'xy's in the denominators
4y-5x = (10x+10y+3xy)/10
Cross multiplying, we get
40y-50x = 10x+10y+3xy
10x+10y+3xy-40y+50x=0
60x-30y+3xy=0....................... equation (1)
Equation (2) 3xy= 10(y-x)
3xy=10y-10x
-10x+10y-3xy = 0 .................. equation (2)
Solving both the following simplified equations
60x-30y+3xy =0...............(a)
-10x+10y -3xy = 0..............(b)
(a) + (b)
50x - 20y = 0
50x = 20y
x/y = 20/50
x : y :: 2:5
x=2 & y=5
One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the actual answer is- a)320
- b)400
- c)480
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the actual answer is
a)
320
b)
400
c)
480
d)
none of these
|
Raghavendra Sharma answered |
Can you explain the answer of this question below:The denominator of a fraction exceeds the numerator by 2. If 5 be added to the numerator the fraction increases by unity. The fraction is.
- A:
5/7
- B:
1/3
- C:
7/9
- D:
3/5
The answer is d.
The denominator of a fraction exceeds the numerator by 2. If 5 be added to the numerator the fraction increases by unity. The fraction is.
5/7
1/3
7/9
3/5
|
Avantika Chakraborty answered |
Let numerator be: x
Let denominator be: x+2
fraction = x/(x+2)
(x+5)/(x+2) = x/(x+2) + 1
(x+5)/(x+2) - x/(x+2) = 1
(x+5 -x)/(x+2)= 1
5/(x+2) = 1
5 = x+2
5-2 = x
x = 3
The fraction is 3/5.
A man rowing at the rate of 5km in an hour in still water takes thrice as much time in going 40km up the river as in going 40km down. Find the rate at which the river flows:- a)9.5 km/hr
- b)2.5 km/hr
- c)12km/hr
- d)None
Correct answer is option 'B'. Can you explain this answer?
A man rowing at the rate of 5km in an hour in still water takes thrice as much time in going 40km up the river as in going 40km down. Find the rate at which the river flows:
a)
9.5 km/hr
b)
2.5 km/hr
c)
12km/hr
d)
None
|
Anuj Roy answered |
Speed of the boat in water =.5 km/hr
Let the speed of the stream be x km/hr
So, the speed of the boat upstream will be (5-x) km / hr
So, the speed of the boat downstream is (5+x) k/hr
Time given to cover 40 km upstream = 3(time taken to cover dowmstream)
⇒40/ (5-x) km/hr = 3(5+x)
⇒1/(5-x)=3(5+x)
⇒5+x=15-3x
⇒x+3x=15-5
⇒4x=10
⇒X=10/4
⇒X=5/2
∴x=2.5 km/hr
Let the speed of the stream be x km/hr
So, the speed of the boat upstream will be (5-x) km / hr
So, the speed of the boat downstream is (5+x) k/hr
Time given to cover 40 km upstream = 3(time taken to cover dowmstream)
⇒40/ (5-x) km/hr = 3(5+x)
⇒1/(5-x)=3(5+x)
⇒5+x=15-3x
⇒x+3x=15-5
⇒4x=10
⇒X=10/4
⇒X=5/2
∴x=2.5 km/hr
Pick up the correct value x for which 
- a)x=0
- b)x=1
- c)x=10
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Pick up the correct value x for which
a)
x=0
b)
x=1
c)
x=10
d)
none of these
|
Naroj Boda answered |
Put x=10
10/0.5-1/0.05+10/0.005-1/0.0005
= 20-20+2000-2000
=0
10/0.5-1/0.05+10/0.005-1/0.0005
= 20-20+2000-2000
=0
Hence, x=10 is the solution of the given equation.
- a)(6, 9)
- b)(9, 6)
- c)(60, 90)
- d)(90, 60)
Correct answer is option 'C'. Can you explain this answer?
a)
(6, 9)
b)
(9, 6)
c)
(60, 90)
d)
(90, 60)
|
Sai Kulkarni answered |
x/5 + y/6 = 27 ------( 1 )
x / 6 + y / 5 = 28 -----( 2 )
Multiply equations with 30 , we get
6x + 5y = 810 -----( 3 )
5x + 6y = 840 ----( 4 )
Multiply equation ( 3 ) with 6, we get
36x + 30y = 4860------( 5 )
Multiply equation with 5 , we get
25x + 30y = 4200 ------( 6 )
Subtract ( 6 ) from ( 5 ), we get
11x = 660
x = 660 / 11
x = 60
Put x = 60 in equation ( 5 ), we get
y = 90
Therefore,
x = 60 and y = 90
A distributor of apple juice has 5000 bottle in the store that it wishes to distribute in a month. From experience it is known that demand D (in number of bottles) is given by D= -2000p2+2000p+17000. The price per bottle that will result zero inventory is- a)Rs. 3
- b)Rs. 5
- c)Rs. 2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
A distributor of apple juice has 5000 bottle in the store that it wishes to distribute in a month. From experience it is known that demand D (in number of bottles) is given by D= -2000p2+2000p+17000. The price per bottle that will result zero inventory is
a)
Rs. 3
b)
Rs. 5
c)
Rs. 2
d)
none of these
|
|
Sameer Sharma answered |
Solution:
Given, the demand function is D= -2000p2 +2000p +17000.
To find the price per bottle that will result in zero inventory, we need to find the price at which demand equals 5000 bottles.
Step 1: Equate demand to 5000 and solve for p.
D = 5000
5000 = -2000p2 +2000p +17000
Step 2: Simplify the equation.
0 = -2000p2 +2000p +12000
0 = -2p2 +2p +12
0 = -p2 + p + 6
Step 3: Solve the quadratic equation.
Using the quadratic formula, we get:
p = (-b ± √(b2 - 4ac)) / 2a
Where a = -1, b = 1, and c = 6.
p = (-1 ± √(12)) / -2
p = (-1 ± 3.464) / -2
p = 2.732 or -1.732
Step 4: Check for extraneous root.
The negative root is extraneous since it does not make sense in the context of the problem.
Step 5: Final answer.
Therefore, the price per bottle that will result in zero inventory is Rs. 3 (approx).
Given, the demand function is D= -2000p2 +2000p +17000.
To find the price per bottle that will result in zero inventory, we need to find the price at which demand equals 5000 bottles.
Step 1: Equate demand to 5000 and solve for p.
D = 5000
5000 = -2000p2 +2000p +17000
Step 2: Simplify the equation.
0 = -2000p2 +2000p +12000
0 = -2p2 +2p +12
0 = -p2 + p + 6
Step 3: Solve the quadratic equation.
Using the quadratic formula, we get:
p = (-b ± √(b2 - 4ac)) / 2a
Where a = -1, b = 1, and c = 6.
p = (-1 ± √(12)) / -2
p = (-1 ± 3.464) / -2
p = 2.732 or -1.732
Step 4: Check for extraneous root.
The negative root is extraneous since it does not make sense in the context of the problem.
Step 5: Final answer.
Therefore, the price per bottle that will result in zero inventory is Rs. 3 (approx).
The fourth part of a number exceeds the sixth part by 4. The number is - a)84
- b)44
- c)48
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The fourth part of a number exceeds the sixth part by 4. The number is
a)
84
b)
44
c)
48
d)
none of these
|
|
Rajat Patel answered |
Let the number be 'x '
Fourth part of a number = x/4
Sixth part = x/ 6
According to the condition of the problem
x/4 =( x/6) +4
x/4 -x/6 = 4
(6x-4x)/24 = 4
2x/24 =4
x/12 = 4
x = 12*4
x = 48
Ans : The number is 48
PIck up the correct value of x for X/30 =2/45
- a)x= 5
- b)x=7
- c)
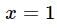
- d)
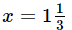
Correct answer is option 'D'. Can you explain this answer?
PIck up the correct value of x for X/30 =2/45
a)
x= 5
b)
x=7
c)
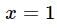
d)
|
Lakshmi Kumar answered |
If we cross multiply;
45x = 30*2
45x = 60
45x = 60
x = 60/ 45
x = 4/3
Time taken by a train to slow down from 80 kmh-1 to 20 kmh-1 with a uniform deceleration of 2 ms-2 is- a)9 s
- b)10 s
- c)8.3 s
- d)8.4 s
Correct answer is option 'C'. Can you explain this answer?
Time taken by a train to slow down from 80 kmh-1 to 20 kmh-1 with a uniform deceleration of 2 ms-2 is
a)
9 s
b)
10 s
c)
8.3 s
d)
8.4 s
|
|
Subhankar Sen answered |
Given:
Initial velocity, u = 80 km/h = 22.22 m/s
Final velocity, v = 20 km/h = 5.56 m/s
Acceleration, a = -2 m/s^2 (negative sign indicates deceleration)
We need to find the time taken by the train to slow down from 80 km/h to 20 km/h with a uniform deceleration of 2 m/s^2.
Using the formula v = u + at, we can find the time taken as follows:
v = u + at
=> t = (v - u) / a
=> t = (5.56 - 22.22) / (-2)
=> t = 8.33 s (approx.)
Therefore, the time taken by the train to slow down from 80 km/h to 20 km/h with a uniform deceleration of 2 m/s^2 is 8.33 s (approx.), which is closest to option (c) 8.3 s.
Initial velocity, u = 80 km/h = 22.22 m/s
Final velocity, v = 20 km/h = 5.56 m/s
Acceleration, a = -2 m/s^2 (negative sign indicates deceleration)
We need to find the time taken by the train to slow down from 80 km/h to 20 km/h with a uniform deceleration of 2 m/s^2.
Using the formula v = u + at, we can find the time taken as follows:
v = u + at
=> t = (v - u) / a
=> t = (5.56 - 22.22) / (-2)
=> t = 8.33 s (approx.)
Therefore, the time taken by the train to slow down from 80 km/h to 20 km/h with a uniform deceleration of 2 m/s^2 is 8.33 s (approx.), which is closest to option (c) 8.3 s.
The sides of an equilateral triangle are shortened by 12 units 13 units and 14 units respectively and a right angle triangle is formed. The side of the equilateral triangle is - a)17 units
- b)16 units
- c)15 units
- d)18 units
Correct answer is option 'A'. Can you explain this answer?
The sides of an equilateral triangle are shortened by 12 units 13 units and 14 units respectively and a right angle triangle is formed. The side of the equilateral triangle is
a)
17 units
b)
16 units
c)
15 units
d)
18 units
|
Aman Chaudhary answered |
Given information:
- An equilateral triangle is shortened by 12 units, 13 units, and 14 units respectively.
- A right-angled triangle is formed from the shortened sides.
To find:
- The side of the equilateral triangle.
Solution:
Let the side of the equilateral triangle be 'x' units.
After shortening,
- The first side of the triangle becomes x - 12 units.
- The second side becomes x - 13 units.
- The third side becomes x - 14 units.
Using the Pythagorean theorem, we can say that:
(x - 12)^2 + (x - 13)^2 = (x - 14)^2
On solving this equation, we get:
x = 17 units
Therefore, the side of the equilateral triangle is 17 units.
Answer: Option A (17 units)
- An equilateral triangle is shortened by 12 units, 13 units, and 14 units respectively.
- A right-angled triangle is formed from the shortened sides.
To find:
- The side of the equilateral triangle.
Solution:
Let the side of the equilateral triangle be 'x' units.
After shortening,
- The first side of the triangle becomes x - 12 units.
- The second side becomes x - 13 units.
- The third side becomes x - 14 units.
Using the Pythagorean theorem, we can say that:
(x - 12)^2 + (x - 13)^2 = (x - 14)^2
On solving this equation, we get:
x = 17 units
Therefore, the side of the equilateral triangle is 17 units.
Answer: Option A (17 units)
Ten years ago the age of a father was four times of his son. Ten years hence the age of the father will be twice that of his son. The present ages of the father and the son are.- a)(50,20)
- b)(60,20)
- c)(55,25)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Ten years ago the age of a father was four times of his son. Ten years hence the age of the father will be twice that of his son. The present ages of the father and the son are.
a)
(50,20)
b)
(60,20)
c)
(55,25)
d)
none of these
|
|
Ishani Rane answered |
F-10 = 4(S-10) on solving this one gets F - 4S = -30....1
F = 10 = 2(S+10) on solving this one gets F - 2S = 10....2
solve both the equation and you get F= 50 S = 20
The wages of 8 men and 6 boys amount to Rs. 33. If 4 men earn Rs. 4.50 more than 5 boys determine the wages of each man and boy.- a)(Rs. 1.50, Rs. 3)
- b)(Rs. 3, Rs. 1.50)
- c)(Rs. 2.50, Rs. 2)
- d)(Rs. 2, Rs. 2.50)
Correct answer is option 'B'. Can you explain this answer?
The wages of 8 men and 6 boys amount to Rs. 33. If 4 men earn Rs. 4.50 more than 5 boys determine the wages of each man and boy.
a)
(Rs. 1.50, Rs. 3)
b)
(Rs. 3, Rs. 1.50)
c)
(Rs. 2.50, Rs. 2)
d)
(Rs. 2, Rs. 2.50)
|
Arun Khanna answered |
Let the wage of 1 man be rs x and the wage of 1 boy be rs y.
Now, 8x+6y=33
and, 4x=4.5+5y
also, 8x=2(4x)=2(4.5+5y)=9+10y
So,8x=9+10y
Thus, 9+10y+6y=33
9+16y=33
16y=33–9
16y=24
y=24/16
y=1.5
Now, 8x+6(1.5)=33
8x+9=33
8x=33–9
8x=24
x=24/8
x=3
So, the wage of each man is rs 3 while the wage of each boy is rs 1.5.
The simultaneous equations 7x–3y = 31, 9x–5y = 41 have solutions given by- a)(–4, –1)
- b)(–1, 4)
- c)(4, –1)
- d)(3, 7)
Correct answer is option 'C'. Can you explain this answer?
The simultaneous equations 7x–3y = 31, 9x–5y = 41 have solutions given by
a)
(–4, –1)
b)
(–1, 4)
c)
(4, –1)
d)
(3, 7)
|
Bhaskar Sharma answered |
Solution:
Given equations are 7x3y = 31, 9x5y = 41.
We need to find the solutions of the equations.
Method:
Let us solve the given equations using the method of elimination.
Multiplying the first equation by 5 and the second equation by 3, we get
35x15y = 155 …..(1)
27x15y = 123 …..(2)
Subtracting equation (2) from equation (1), we get
8x0y = 32
8x = 32
x = 4
Substituting the value of x in equation (1), we get
35x3y = 155
105y = 155
y = 155/105 = 31/21
Therefore, the solution of the given equations is (x, y) = (4, 31/21)
On simplification, we get
(x, y) = (4, 1.476)
Hence, option (c) is the correct answer.
Given equations are 7x3y = 31, 9x5y = 41.
We need to find the solutions of the equations.
Method:
Let us solve the given equations using the method of elimination.
Multiplying the first equation by 5 and the second equation by 3, we get
35x15y = 155 …..(1)
27x15y = 123 …..(2)
Subtracting equation (2) from equation (1), we get
8x0y = 32
8x = 32
x = 4
Substituting the value of x in equation (1), we get
35x3y = 155
105y = 155
y = 155/105 = 31/21
Therefore, the solution of the given equations is (x, y) = (4, 31/21)
On simplification, we get
(x, y) = (4, 1.476)
Hence, option (c) is the correct answer.
If x/4 = y/3 = z/2 then what will be the value of x , y , z if 7x + 8y + 5z = 62a)(4, 3, 2)b)(2, 3, 4)c)(3, 4, 2)d)(4, 2, 3)Correct answer is option 'A'. Can you explain this answer?
|
|
Lakshmi Kaur answered |
Let x/4=y/3=z/2=k
x=4k
y=3k
z=2k
7x+8y+5z=62
⇒7*4k+8*3k+5*2k=62
⇒28k+24k+10k=62
⇒62k=62
⇒k=62/62
∴k=1
x=4k
y=3k
z=2k
7x+8y+5z=62
⇒7*4k+8*3k+5*2k=62
⇒28k+24k+10k=62
⇒62k=62
⇒k=62/62
∴k=1
Hence,
x= 4
y=3
z= 2
The Root of the equation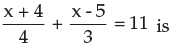 
- a)20
- b)10
- c)2
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The Root of the equation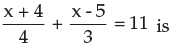
a)
20
b)
10
c)
2
d)
none of these
|
|
Preeti Khanna answered |
LCM of 4 and 3 = 12 , then 3(x+4) +4(x-5)=11 × 12 then 140/7 = 20 Answer
Three persons Mr. Roy, Mr. Paul and Mr. Singh together have Rs. 51. Mr. Paul has Rs. 4 less than Mr. Roy and Mr. Singh has got Rs. 5 less than Mr. Roy. They have the money as.- a)(Rs. 20, Rs. 16, Rs. 15)
- b)(Rs. 15, Rs. 20, Rs. 16)
- c)(Rs. 25, Rs. 11, Rs. 15)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Three persons Mr. Roy, Mr. Paul and Mr. Singh together have Rs. 51. Mr. Paul has Rs. 4 less than Mr. Roy and Mr. Singh has got Rs. 5 less than Mr. Roy. They have the money as.
a)
(Rs. 20, Rs. 16, Rs. 15)
b)
(Rs. 15, Rs. 20, Rs. 16)
c)
(Rs. 25, Rs. 11, Rs. 15)
d)
none of these
|
|
Raghavendra Sharma answered |
Mr. Roy has = x
Mr. Pual has = x-4
Mr. Singh has = x-5
Together they have = 51
Mr. Roy + Mr. Pual + Mr. Singh = 51
x+(x-4)+(x-5)=51
3x-9=51
3x=51+9
3x=60
divide by 3
3x/3=60/3
x=20
Mr. Roy has = x = 20
Mr. Pual has = x-4 = 20-4 = 16
Mr. Singh has = x-5 = 20-5= 15
20+16+15=51
51=51
If x=a, y=b is the solution of the pair of equation x-y=2 and x+y=4 then what will be value of a and b- a) 2,1
- b) 3,1
- c) 4,6
- d) 1,2
Correct answer is option 'B'. Can you explain this answer?
If x=a, y=b is the solution of the pair of equation x-y=2 and x+y=4 then what will be value of a and b
a)
2,1
b)
3,1
c)
4,6
d)
1,2
|
|
Akshay Saini answered |
X=a. y=b
a-b=2
a=2+b_(1)
a+b=4
2+b+b=4 _from (1)
2+2b=4
2b=2
b=1
a-1=2_(b=1)
a=3
ans:(3,1)
a-b=2
a=2+b_(1)
a+b=4
2+b+b=4 _from (1)
2+2b=4
2b=2
b=1
a-1=2_(b=1)
a=3
ans:(3,1)
The line joining (-1,1) and (2,-2) and the line joining (1,2) and (2, k) are perpendicular to each other for the following value of k: - a)1
- b)0
- c)-1
- d)3
Correct answer is option 'D'. Can you explain this answer?
The line joining (-1,1) and (2,-2) and the line joining (1,2) and (2, k) are perpendicular to each other for the following value of k:
a)
1
b)
0
c)
-1
d)
3
|
|
Rutuja Dasgupta answered |
Solution:
The slope of the line joining (-1,1) and (2,-2) is given by
$$m_1=\frac{y_2-y_1}{x_2-x_1}=\frac{-2-1}{2-(-1)}=-\frac{3}{3}=-1$$
Therefore, the equation of this line is
$$y-1=-1(x+1)$$
$$\Rightarrow x+y=0$$
Similarly, the slope of the line joining (1,2) and (2,k) is given by
$$m_2=\frac{y_2-y_1}{x_2-x_1}=\frac{k-2}{2-1}=k-2$$
Therefore, the equation of this line is
$$y-2=(k-2)(x-1)$$
$$\Rightarrow y=kx+(-k+4)$$
Now, as these two lines are perpendicular to each other, their slopes are negative reciprocals of each other. Therefore,
$$m_1 \cdot m_2 = -1$$
$$\Rightarrow -1 \cdot (k-2)=-1$$
$$\Rightarrow k-2=1$$
$$\Rightarrow k=3$$
Therefore, the value of k for which the two lines are perpendicular is 3. Thus, the correct option is (D).
The slope of the line joining (-1,1) and (2,-2) is given by
$$m_1=\frac{y_2-y_1}{x_2-x_1}=\frac{-2-1}{2-(-1)}=-\frac{3}{3}=-1$$
Therefore, the equation of this line is
$$y-1=-1(x+1)$$
$$\Rightarrow x+y=0$$
Similarly, the slope of the line joining (1,2) and (2,k) is given by
$$m_2=\frac{y_2-y_1}{x_2-x_1}=\frac{k-2}{2-1}=k-2$$
Therefore, the equation of this line is
$$y-2=(k-2)(x-1)$$
$$\Rightarrow y=kx+(-k+4)$$
Now, as these two lines are perpendicular to each other, their slopes are negative reciprocals of each other. Therefore,
$$m_1 \cdot m_2 = -1$$
$$\Rightarrow -1 \cdot (k-2)=-1$$
$$\Rightarrow k-2=1$$
$$\Rightarrow k=3$$
Therefore, the value of k for which the two lines are perpendicular is 3. Thus, the correct option is (D).
A man sells 6 radios and 4 televisions for Rs. 18,480. If 14 radios and 2 televisions are sold for the same amount, what is the price of a televisions?- a)Rs. 1,848
- b)Rs. 840
- c)Rs. 1,680
- d)Rs. 3,360
Correct answer is option 'D'. Can you explain this answer?
A man sells 6 radios and 4 televisions for Rs. 18,480. If 14 radios and 2 televisions are sold for the same amount, what is the price of a televisions?
a)
Rs. 1,848
b)
Rs. 840
c)
Rs. 1,680
d)
Rs. 3,360
|
|
Aarya Sharma answered |
Given:
- Selling 6 radios + 4 televisions = Rs. 18,480
- Selling 14 radios + 2 televisions = Rs. 18,480
To find:
- Price of 1 television
Solution:
Let the cost of 1 radio be x and the cost of 1 television be y.
From the given information, we can form the following equations:
6x + 4y = 18,480 ...(1)
14x + 2y = 18,480 ...(2)
We need to find the value of y.
Method 1: Using elimination method
Multiplying equation (1) by 7 and subtracting it from equation (2) multiplied by 3, we get:
42x + 12y = 129,360
-(21x + 12y = 129,480)
------------------------
21x = -120
x = -120/21
Substituting the value of x in equation (1), we get:
6(-120/21) + 4y = 18,480
-360 + 4y = 18,480
4y = 18,840
y = 4,710
Therefore, the price of 1 television is Rs. 4,710.
Method 2: Using substitution method
From equation (1), we can write:
6x = 18,480 - 4y
x = (18,480 - 4y)/6
Substituting this value of x in equation (2), we get:
14((18,480 - 4y)/6) + 2y = 18,480
Simplifying this equation, we get:
y = 3,360/2 = 1,680
Therefore, the price of 1 television is Rs. 1,680.
However, we need to check if this solution satisfies the first equation as well.
Substituting y = 1,680 in equation (1), we get:
6x + 4(1,680) = 18,480
6x = 11,040
x = 1,840
Therefore, the cost of 1 radio is Rs. 1,840.
Hence, the solution is:
- Price of 1 television = Rs. 1,680
- Price of 1 radio = Rs. 1,840
- Selling 6 radios + 4 televisions = Rs. 18,480
- Selling 14 radios + 2 televisions = Rs. 18,480
To find:
- Price of 1 television
Solution:
Let the cost of 1 radio be x and the cost of 1 television be y.
From the given information, we can form the following equations:
6x + 4y = 18,480 ...(1)
14x + 2y = 18,480 ...(2)
We need to find the value of y.
Method 1: Using elimination method
Multiplying equation (1) by 7 and subtracting it from equation (2) multiplied by 3, we get:
42x + 12y = 129,360
-(21x + 12y = 129,480)
------------------------
21x = -120
x = -120/21
Substituting the value of x in equation (1), we get:
6(-120/21) + 4y = 18,480
-360 + 4y = 18,480
4y = 18,840
y = 4,710
Therefore, the price of 1 television is Rs. 4,710.
Method 2: Using substitution method
From equation (1), we can write:
6x = 18,480 - 4y
x = (18,480 - 4y)/6
Substituting this value of x in equation (2), we get:
14((18,480 - 4y)/6) + 2y = 18,480
Simplifying this equation, we get:
y = 3,360/2 = 1,680
Therefore, the price of 1 television is Rs. 1,680.
However, we need to check if this solution satisfies the first equation as well.
Substituting y = 1,680 in equation (1), we get:
6x + 4(1,680) = 18,480
6x = 11,040
x = 1,840
Therefore, the cost of 1 radio is Rs. 1,840.
Hence, the solution is:
- Price of 1 television = Rs. 1,680
- Price of 1 radio = Rs. 1,840
The equation x2 –(p+4)x + 2p + 5 = 0 has equal roots the values of p will be.- a)± 1
- b)2
- c)± 2
- d)–2
Correct answer is option 'C'. Can you explain this answer?
The equation x2 –(p+4)x + 2p + 5 = 0 has equal roots the values of p will be.
a)
± 1
b)
2
c)
± 2
d)
–2
|
|
Rithika Nair answered |
Given equation: x^2 + (4p)x + 2p + 5 = 0
For equal roots, the discriminant (b^2 - 4ac) of the quadratic equation must be equal to zero.
So, we have:
(4p)^2 - 4(1)(2p + 5) = 0
16p^2 - 8p - 20 = 0
Dividing throughout by 4, we get:
4p^2 - 2p - 5 = 0
Using the quadratic formula, we get:
p = [2 ± √(4 + 80)]/8
p = [2 ± √84]/8
p = [1 ± √21]/4
Since we are given that the roots are equal, we must have only one value of p, so we take the positive value of the square root:
p = (1 + √21)/4
Therefore, the correct answer is option C.
For equal roots, the discriminant (b^2 - 4ac) of the quadratic equation must be equal to zero.
So, we have:
(4p)^2 - 4(1)(2p + 5) = 0
16p^2 - 8p - 20 = 0
Dividing throughout by 4, we get:
4p^2 - 2p - 5 = 0
Using the quadratic formula, we get:
p = [2 ± √(4 + 80)]/8
p = [2 ± √84]/8
p = [1 ± √21]/4
Since we are given that the roots are equal, we must have only one value of p, so we take the positive value of the square root:
p = (1 + √21)/4
Therefore, the correct answer is option C.
If the root of the equation x2–8x+m = 0 exceeds the other by 4 then the value of m is- a)m = 10
- b)m = 11
- c)m = 9
- d)m = 12
Correct answer is option 'D'. Can you explain this answer?
If the root of the equation x2–8x+m = 0 exceeds the other by 4 then the value of m is
a)
m = 10
b)
m = 11
c)
m = 9
d)
m = 12
|
|
Priya Patel answered |
In the given equation x2 - 8x + m = 0, constant term "m" is positive.
The two factors of m must satisfy the following two conditions.
(i) Sum of the two factors of "m" must be equal to the middle term - 8.
(ii) One root of the equation must exceed the other by 4. That is, there must be a difference of 4 between the two roots.
The above two conditions can be met, only if the two factors of "m" are - 2 and - 6
Then, we have
m = (- 2) ⋅ (- 6)
m = 12
Hence, the value of m is 12.
The value of k for which the points (k,1), (5, 5) and (10,7) may be collinear is: - a)K=-5
- b)k=7
- c)k=9
- d)k=1
Correct answer is option 'A'. Can you explain this answer?
The value of k for which the points (k,1), (5, 5) and (10,7) may be collinear is:
a)
K=-5
b)
k=7
c)
k=9
d)
k=1
|
|
Meera Basak answered |
Solution:
To check whether the given points are collinear or not, we can use the slope formula.
Let the slope of the line passing through the points (k,1) and (5,5) be m1.
m1 = (5 - 1) / (5 - k) = 4 / (5 - k)
Let the slope of the line passing through the points (5,5) and (10,7) be m2.
m2 = (7 - 5) / (10 - 5) = 2 / 5
If the three points are collinear, then the slopes of the two lines passing through them must be equal.
Therefore, we can equate m1 and m2.
4 / (5 - k) = 2 / 5
Cross-multiplying, we get:
20 = 2(5 - k)
10 - k = 10
k = 10 - 10
k = -5
Therefore, the value of k for which the given points are collinear is -5.
Hence, option A is the correct answer.
To check whether the given points are collinear or not, we can use the slope formula.
Let the slope of the line passing through the points (k,1) and (5,5) be m1.
m1 = (5 - 1) / (5 - k) = 4 / (5 - k)
Let the slope of the line passing through the points (5,5) and (10,7) be m2.
m2 = (7 - 5) / (10 - 5) = 2 / 5
If the three points are collinear, then the slopes of the two lines passing through them must be equal.
Therefore, we can equate m1 and m2.
4 / (5 - k) = 2 / 5
Cross-multiplying, we get:
20 = 2(5 - k)
10 - k = 10
k = 10 - 10
k = -5
Therefore, the value of k for which the given points are collinear is -5.
Hence, option A is the correct answer.
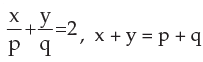are satisfied by the values given by the pair.- a)(x=p, y=q)
- b)(x=q, y=p)
- c)(x=1, y=1)
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
are satisfied by the values given by the pair.a)
(x=p, y=q)
b)
(x=q, y=p)
c)
(x=1, y=1)
d)
none of these
|
|
Maheshwar Datta answered |
According to the given question,
i ) x + y = p + q
x = p + q - y ---------( 1 )
ii ) x / p + y / q = 2
Multiply each term with pq we get
qx + py = 2pq ---------( 2 )
Put x value , from ( 1 ) in equation ( 2)
q( p + q - y) + py = 2pq
pq + q^2 - qy + py = 2pq
- qy + py = 2pq - pq - q^2
y ( - q + p) = pq - q^2
y ( p - q ) = q ( p - q )
y = q ( p - q )/ ( p - q )
y = q -----( 3 )
Put y = q in ( 1 )
x = p + q - q
x = p
Therefore ,
x = p and y = q
has got the solution as
Of two numbers, 1/5th of the greater is equal to 1/3rd of the smaller and their sum is 16. The numbers are: - a)(6, 10)
- b)(9, 7)
- c)(12, 4)
- d)(11, 5)
Correct answer is option 'A'. Can you explain this answer?
Of two numbers, 1/5th of the greater is equal to 1/3rd of the smaller and their sum is 16. The numbers are:
a)
(6, 10)
b)
(9, 7)
c)
(12, 4)
d)
(11, 5)
|
|
Aarya Sharma answered |
Given:
- 1/5th of the greater number = 1/3rd of the smaller number
- Sum of the two numbers = 16
To find: The two numbers
Solution:
Let's assume the two numbers as 'a' and 'b', where 'a' is greater than 'b'.
From the first condition, we have:
- 1/5a = 1/3b [as 1/5th of the greater number is equal to 1/3rd of the smaller number]
Simplifying the above equation, we get:
- b = 3/5a
Substituting the value of 'b' in terms of 'a' in the second equation:
- a + b = 16
- a + 3/5a = 16 [as b = 3/5a]
- 8/5a = 16
- a = 10
Substituting the value of 'a' in the equation 'b = 3/5a', we get:
- b = 3/5(10) = 6
Therefore, the two numbers are 10 and 6. Hence, option 'A' is the correct answer.
Answer: Option 'A' (6, 10)
- 1/5th of the greater number = 1/3rd of the smaller number
- Sum of the two numbers = 16
To find: The two numbers
Solution:
Let's assume the two numbers as 'a' and 'b', where 'a' is greater than 'b'.
From the first condition, we have:
- 1/5a = 1/3b [as 1/5th of the greater number is equal to 1/3rd of the smaller number]
Simplifying the above equation, we get:
- b = 3/5a
Substituting the value of 'b' in terms of 'a' in the second equation:
- a + b = 16
- a + 3/5a = 16 [as b = 3/5a]
- 8/5a = 16
- a = 10
Substituting the value of 'a' in the equation 'b = 3/5a', we get:
- b = 3/5(10) = 6
Therefore, the two numbers are 10 and 6. Hence, option 'A' is the correct answer.
Answer: Option 'A' (6, 10)
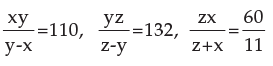
- a)(12, 11, 10)
- b)(10, 11, 12)
- c)(11, 10, 12)
- d)(12, 10, 11)
Correct answer is option 'B'. Can you explain this answer?
a)
(12, 11, 10)
b)
(10, 11, 12)
c)
(11, 10, 12)
d)
(12, 10, 11)
|
|
Sagarika Pillai answered |
Put the value x=10, y=11and z=12
for example first equation is xy/y-x=110
put x=10and y=11
10*11/11-10
=110
for example first equation is xy/y-x=110
put x=10and y=11
10*11/11-10
=110
We can solve this question by option checking
If you try to solve this question it will take too much time and you don't have enought time.
If you try to solve this question it will take too much time and you don't have enought time.
If the length of a rectangle is 5 cm more than the breadth and if the perimeter of the rectangle is 40cm, then the length & breadth of the rectangle with be: - a)7.5cm, 2.5cm
- b)10cm, 5cm
- c)12.5cm, 7.5cm
- d)15.5cm, 10.5cm
Correct answer is option 'C'. Can you explain this answer?
If the length of a rectangle is 5 cm more than the breadth and if the perimeter of the rectangle is 40cm, then the length & breadth of the rectangle with be:
a)
7.5cm, 2.5cm
b)
10cm, 5cm
c)
12.5cm, 7.5cm
d)
15.5cm, 10.5cm
|
|
Sahil Malik answered |
Let the breadth of the rectangle be x cm.
Then, the length of the rectangle is (x + 5) cm.
Perimeter of the rectangle = 2(length + breadth)
40 = 2[(x + 5) + x]
40 = 2(2x + 5)
40 = 4x + 10
4x = 30
x = 7.5
Therefore, the length of the rectangle = x + 5 = 12.5 cm.
Then, the length of the rectangle is (x + 5) cm.
Perimeter of the rectangle = 2(length + breadth)
40 = 2[(x + 5) + x]
40 = 2(2x + 5)
40 = 4x + 10
4x = 30
x = 7.5
Therefore, the length of the rectangle = x + 5 = 12.5 cm.
Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are :- a)(36, 42)
- b)(45, 36)
- c)(50, 41)
- d)(55, 46)
Correct answer is option 'B'. Can you explain this answer?
Two numbers are such that twice the greater number exceeds twice the smaller one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are :
a)
(36, 42)
b)
(45, 36)
c)
(50, 41)
d)
(55, 46)
|
|
Sahil Malik answered |
Given information:
- Twice the greater number exceeds twice the smaller number by 18
- 1/3 of the smaller number + 1/5 of the greater number = 21
To find:
- The two numbers
Solution:
Let the two numbers be x and y, where x is the smaller number and y is the greater number.
From the first statement, we can write:
2y = 2x + 18
Simplifying this equation, we get:
y - x = 9 ...(1)
From the second statement, we can write:
(1/3)x + (1/5)y = 21
Multiplying both sides by 15 to get rid of the fractions, we get:
5x + 3y = 315 ...(2)
Now we have two equations with two variables. We can solve for x and y by eliminating one of the variables.
Multiplying equation (1) by 3, we get:
3y - 3x = 27
Adding this equation to equation (2), we get:
5x + 3y - 3x + 27 = 315
Simplifying this equation, we get:
2x + 3y = 288
Multiplying equation (1) by 2, we get:
2y - 2x = 18
Adding this equation to equation (2), we get:
5x + 2y - 2x + 18 = 315
Simplifying this equation, we get:
3x + 2y = 297
Now we have two equations with two variables again. We can solve for x and y by eliminating one of the variables.
Multiplying the first equation by 2 and subtracting the second equation from it, we get:
(2x + 18) - (3x + 2y) = 18
Simplifying this equation, we get:
-x - 2y = -18
Multiplying equation (1) by -2 and adding it to this equation, we get:
-2y + 2x + 2y = -18 - 18
Simplifying this equation, we get:
x = 36
Substituting x = 36 in equation (1), we get:
y - 36 = 9
Simplifying this equation, we get:
y = 45
Therefore, the two numbers are 36 and 45.
Hence, the correct answer is option (B).
- Twice the greater number exceeds twice the smaller number by 18
- 1/3 of the smaller number + 1/5 of the greater number = 21
To find:
- The two numbers
Solution:
Let the two numbers be x and y, where x is the smaller number and y is the greater number.
From the first statement, we can write:
2y = 2x + 18
Simplifying this equation, we get:
y - x = 9 ...(1)
From the second statement, we can write:
(1/3)x + (1/5)y = 21
Multiplying both sides by 15 to get rid of the fractions, we get:
5x + 3y = 315 ...(2)
Now we have two equations with two variables. We can solve for x and y by eliminating one of the variables.
Multiplying equation (1) by 3, we get:
3y - 3x = 27
Adding this equation to equation (2), we get:
5x + 3y - 3x + 27 = 315
Simplifying this equation, we get:
2x + 3y = 288
Multiplying equation (1) by 2, we get:
2y - 2x = 18
Adding this equation to equation (2), we get:
5x + 2y - 2x + 18 = 315
Simplifying this equation, we get:
3x + 2y = 297
Now we have two equations with two variables again. We can solve for x and y by eliminating one of the variables.
Multiplying the first equation by 2 and subtracting the second equation from it, we get:
(2x + 18) - (3x + 2y) = 18
Simplifying this equation, we get:
-x - 2y = -18
Multiplying equation (1) by -2 and adding it to this equation, we get:
-2y + 2x + 2y = -18 - 18
Simplifying this equation, we get:
x = 36
Substituting x = 36 in equation (1), we get:
y - 36 = 9
Simplifying this equation, we get:
y = 45
Therefore, the two numbers are 36 and 45.
Hence, the correct answer is option (B).
A man went to the Reserve Bank of India with Rs. 1, 000. He asked the cashier to give him Rs. 5 and Rs.10 notes only in return. The man got 175 notes in all. Find how many notes of Rs. 5 and Rs. 10 did he receive?- a)25, 150
- b)40, 110
- c)150, 25
- d)None
Correct answer is option 'C'. Can you explain this answer?
A man went to the Reserve Bank of India with Rs. 1, 000. He asked the cashier to give him Rs. 5 and Rs.10 notes only in return. The man got 175 notes in all. Find how many notes of Rs. 5 and Rs. 10 did he receive?
a)
25, 150
b)
40, 110
c)
150, 25
d)
None
|
|
Srsps answered |
Let the number of notes of 500 and 1000 rupees are x and y respectively.
Given, the sum of number of of 500 and 1000 rupee notes is 175
=> x + y = 175 ...1
Again total value of 500 and 1000 rupee notes is 100000
=> 500x + 1000y = 100000
=> 500(x + 2y) = 100000
=> x + 2y = 100000/500
=> x + 2y = 1000/5
=> x + 2y = 200 . .2
Subtract equation 1 and 2, we get
x + 2y - x - y = 200 - 175
=> y = 25
From equation 1, we get
x + 25 = 175
=> x = 175 - 25
=> x = 150
So, the number of notes of 500 is 150
and the number of notes of 1000 is 25
If œ ß be the roots of the equation 2x2 – 4x – 3 = 0 the value of α2 + β2 is- a)5
- b)7
- c)3
- d)– 4
Correct answer is option 'B'. Can you explain this answer?
If œ ß be the roots of the equation 2x2 – 4x – 3 = 0 the value of α2 + β2 is
a)
5
b)
7
c)
3
d)
– 4
|
|
Nandini Iyer answered |
(a+b)^2=a^2+b^2+2ab
a^2+b^2=(a+b)^2–2ab
Sum of roots =-b/a=-(-4)/2=2
product of roots = c/a=-3/2
=>a^2+b^2=(2^2)-2*(-3/2)
=7
The solution of the set of equations 3x + 4y = 7, 4x – y = 3 is- a)(1, –1)
- b)(1, 1)
- c)(2, 1)
- d)(1, –2)
Correct answer is option 'B'. Can you explain this answer?
The solution of the set of equations 3x + 4y = 7, 4x – y = 3 is
a)
(1, –1)
b)
(1, 1)
c)
(2, 1)
d)
(1, –2)
|
|
Siddharth Sen answered |
Here 3x+4y=7.........(1)
4x-y=3........(2)
eq(1) * 1 --- 3x +4y =7
.
eq(2) * 4--- 16x -4y =12
.
eq(2) * 4--- 16x -4y =12
adding eq(1) with eq(2)
................................................................
19x=19
19x=19
=>x=19/19=1 ........
from eq(1) 3x + 4y=7
=>3*1 + 4y=7
=>4y = 7-3=4
=> y= 4/4=1 .
One root of the equation:
X2-2(5+m)x+3(7+m)=0 is reciprocal of the other.
Find the value of M.
- a)-20/3
- b) 7
- c)1/7
- d) -1/7
Correct answer is option 'A'. Can you explain this answer?
One root of the equation:
X2-2(5+m)x+3(7+m)=0 is reciprocal of the other.
Find the value of M.
X2-2(5+m)x+3(7+m)=0 is reciprocal of the other.
Find the value of M.
a)
-20/3
b)
7
c)
1/7
d)
-1/7
|
|
Harshad Kapoor answered |
Given equation: X2-2(5 m)x 3(7 m)=0
Let the roots of the equation be a and b.
It is given that a and b are reciprocals of each other.
Therefore, ab = 1.
Using sum and product of roots formulae, we get:
a + b = 2(5 m)/1 = 10 m
ab = 3(7 m)/1 = 21 m
Substituting ab = 1, we get:
21 m = 1
m = 1/21
To check whether a and b are reciprocals of each other or not, we can find a and b using the quadratic formula:
a = [2(5 m) ± √(4(25 m2) - 4(3)(7 m))]/2
a = 5 m ± √(25 m2 - 21 m)
b = 1/a
If we substitute m = 1/21, we get:
a = 5/3 or 7
b = 3/5 or 1/7
Since a and b are reciprocals of each other, the only possible value of m is when a = 3/5 and b = 5/3, which implies m = -20/3.
Therefore, the correct answer is option A.
Let the roots of the equation be a and b.
It is given that a and b are reciprocals of each other.
Therefore, ab = 1.
Using sum and product of roots formulae, we get:
a + b = 2(5 m)/1 = 10 m
ab = 3(7 m)/1 = 21 m
Substituting ab = 1, we get:
21 m = 1
m = 1/21
To check whether a and b are reciprocals of each other or not, we can find a and b using the quadratic formula:
a = [2(5 m) ± √(4(25 m2) - 4(3)(7 m))]/2
a = 5 m ± √(25 m2 - 21 m)
b = 1/a
If we substitute m = 1/21, we get:
a = 5/3 or 7
b = 3/5 or 1/7
Since a and b are reciprocals of each other, the only possible value of m is when a = 3/5 and b = 5/3, which implies m = -20/3.
Therefore, the correct answer is option A.
A number between 10 and 100 is five times the sum of its digits. If 9 be added to it the digits are reversed find the number.- a)54
- b)53
- c)45
- d)55
Correct answer is option 'C'. Can you explain this answer?
A number between 10 and 100 is five times the sum of its digits. If 9 be added to it the digits are reversed find the number.
a)
54
b)
53
c)
45
d)
55
|
|
Arun Khanna answered |
Let the number be 10 x + y
sum of its numbers = x+ y
according to the sum
10 x + y = 5(x + y)
10 x + y = 5 x + 5 y
10 x - 5 x = 5 y - y
5 x - 4 y = 0
if 9 is added the digits are reversed
⇒ 10 x + y + 9 = 10 y + x
10 x - x + 9 = 10 y - y
9 x - 9 y = - 9
x - y = - 1
simultaneous equation 5 x - 4 y = 0
x - y = -1
1(5 x - 4 y = 0)
5(x - y = -1)
5 x - 4 y = 0 →a
5 x - 5 y = -5→b
On subtracting b from a
5 x - 4 y = 0
- 5 x + 5 y = 5
y = 5
On substituting y = 5 in x - y = - 1
we get x = 4
The number is 10 x + y = 10(4) + 5 = 45
One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the number was - a)320
- b)400
- c)480
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the number was
a)
320
b)
400
c)
480
d)
none of these
|
|
Hrishikesh Pillai answered |
Problem: One student is asked to divide a half of a number by 6 and other half by 4 and then to add the two quantities. Instead of doing so the student divides the given number by 5. If the answer is 4 short of the correct answer then the number was
- a)320
- b)400
- c)480
- d)none of these
Solution:
Let's assume the given number as 'x'.
According to the given question, one half of the number divided by 6 and the other half divided by 4 are added. So, the expression for the given question is:
(x/2)/6 + (x/2)/4
Simplifying the above expression, we get:
x/12 + x/8 = (2x+3x)/24 = 5x/24
The above expression is the correct answer if the student had followed the instructions correctly.
But the student divided the given number by 5. So, the expression the student got is:
x/5
According to the given question, the student's answer is 4 less than the correct answer. So, we can write:
x/5 = 5x/24 - 4
Simplifying the above equation, we get:
24x = 25x - 480
x = 480
Therefore, the given number is 480.
Thus, the correct option is (c) 480.
The solution of the equation (p+2) (p–3) + (p+3) (p–4) = p(2p–5) is- a)6
- b)7
- c)5
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The solution of the equation (p+2) (p–3) + (p+3) (p–4) = p(2p–5) is
a)
6
b)
7
c)
5
d)
none of these
|
Gowri Chakraborty answered |
(p+2)(p-3)+(p+3)(p-4)=p(2p-5)
p^2-3p+2p-6+p^2-4p+3p-12=2p^2-5p
2p^2-2p-18=2p^2-5p
-2p+5p=18
3p=18
p=6
Find the fraction which is equal to 1/2 when both its numerator and denominator are increased by 2. It is equal to 3/4 when both are incresed by 12.- a)3/8
- b)5/8
- c)2/3
- d)none
Correct answer is option 'A'. Can you explain this answer?
Find the fraction which is equal to 1/2 when both its numerator and denominator are increased by 2. It is equal to 3/4 when both are incresed by 12.
a)
3/8
b)
5/8
c)
2/3
d)
none
|
|
Arun Khanna answered |
Let the numerator be x and denomentar be y
(x+2)/(y+2)=1/2
2x+4=y+2
2x-y=-2
4x-2y=-4
when
(x+12)/(y+12)=3/4
4x+48=3y+36
4x-3y=-12
from both the eq
y=8
x=3
so fraction is
3/8
If x=m is one of the solutions of the equation 2x2+5x-m=0 the possible values of m are- a)(0, 2)
- b)(0, -2)
- c)(0, 1)
- d)(1, -1)
Correct answer is option 'B'. Can you explain this answer?
If x=m is one of the solutions of the equation 2x2+5x-m=0 the possible values of m are
a)
(0, 2)
b)
(0, -2)
c)
(0, 1)
d)
(1, -1)
|
|
Sameer Basu answered |
Ans.
Option (b)
If x = m is a solution of 2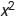
+ 5x - m = 0, then
we can write given equation as,
2m2 + 5m - m = 0
⇒⇒ 2m2 + 4m = 0
⇒⇒ 2m (m + 2) = 0
⇒⇒ 2m = 0 or m + 2 = 0
⇒⇒ m = 0 or m = - 2
Thus, (0, -2) is the solution set for the same.
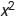+ 5x - m = 0, thenwe can write given equation as,
2m2 + 5m - m = 0
⇒⇒ 2m2 + 4m = 0
⇒⇒ 2m (m + 2) = 0
⇒⇒ 2m = 0 or m + 2 = 0
⇒⇒ m = 0 or m = - 2
Thus, (0, -2) is the solution set for the same.
Chapter doubts & questions for Equations and Matrices (Old Scheme) - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Equations and Matrices (Old Scheme) - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
114 videos|164 docs|98 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup