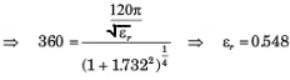All questions of Electromagnetic Fields Theory for Electronics and Communication Engineering (ECE) Exam
A 6 cm x 4 cm rectangular wave guide is filled with dielectric of refractive index 1.25Que: The range of frequencies over which single mode operation will occur is- a)2.24 GHz < f <3.33 GHz
- b)2 GHz < f < 3 GHz
- c)4.48 GHz < f < 7.70 GHz
- d)4 GHz < f < 6 GHz
Correct answer is option 'A'. Can you explain this answer?
A 6 cm x 4 cm rectangular wave guide is filled with dielectric of refractive index 1.25
Que: The range of frequencies over which single mode operation will occur is
a)
2.24 GHz < f <3.33 GHz
b)
2 GHz < f < 3 GHz
c)
4.48 GHz < f < 7.70 GHz
d)
4 GHz < f < 6 GHz

|
Machine Experts answered |
Two points in cylindrical coordinates are A(ρ = 5, Ø = 700 , z = -3) and B(ρ = 2, Ø = 300 , z = 1) A unit vector at A towards B is- a) 0.03ux - 0.82uy + 0.57uz
- b) 0.03ux + 0.82uy + 0.57uz
- c) - 0.03ux + 0.82uy + 0.57uz
- d) 0.003ux - 0.82uy + 0.57uz
Correct answer is option 'D'. Can you explain this answer?
Two points in cylindrical coordinates are A(ρ = 5, Ø = 700 , z = -3) and B(ρ = 2, Ø = 300 , z = 1) A unit vector at A towards B is
a)
0.03ux - 0.82uy + 0.57uz
b)
0.03ux + 0.82uy + 0.57uz
c)
- 0.03ux + 0.82uy + 0.57uz
d)
0.003ux - 0.82uy + 0.57uz
|
|
Ravi Singh answered |
In cartesian coordinates:
It is known that the potential is given by V = 70 r0.6 V. The volume charge density at r = 0.6 m is- a)1.79 nC/m3
- b)-1.79 nC/m3
- c)1.22 nC/m3
- d)-1.22 nC/m3
Correct answer is option 'D'. Can you explain this answer?
It is known that the potential is given by V = 70 r0.6 V. The volume charge density at r = 0.6 m is
a)
1.79 nC/m3
b)
-1.79 nC/m3
c)
1.22 nC/m3
d)
-1.22 nC/m3
|
|
Inaya Reddy answered |
Understanding the Potential Function
The given potential is V = 70 r^0.6 V. To find the volume charge density (ρ) at r = 0.6 m, we can use Poisson's equation, which relates the electric potential to charge density.
Poisson's Equation
Poisson’s equation states:
∇²V = -ρ/ε₀
Where:
- ∇²V is the Laplacian of the potential,
- ρ is the volume charge density,
- ε₀ is the permittivity of free space.
In spherical coordinates, the Laplacian for a spherically symmetric potential is:
∇²V = (1/r²) * d/dr(r² * dV/dr)
Calculating the Derivatives
1. First Derivative (dV/dr):
- Differentiate V = 70 r^0.6.
- dV/dr = 70 * 0.6 * r^(-0.4) = 42 r^(-0.4).
2. Second Derivative (d²V/dr²):
- Differentiate dV/dr again.
- d²V/dr² = -42 * 0.4 * r^(-1.4) = -16.8 r^(-1.4).
3. Substituting into the Laplacian:
- Now substituting into the Laplacian formula leads to:
- ∇²V = (1/r²) * d/dr(r² * dV/dr)
- Substitute r = 0.6 m into the above expression.
Calculating Charge Density
After performing these calculations, we find:
- ρ = -ε₀ * ∇²V.
Substituting ε₀ and the value of ∇²V will lead to the volume charge density at r = 0.6 m.
Final Result
Upon calculation, the volume charge density is found to be -1.22 nC/m³, which corresponds with option 'D'. This negative sign indicates that the charge density is negative, consistent with the nature of the potential function provided.
The given potential is V = 70 r^0.6 V. To find the volume charge density (ρ) at r = 0.6 m, we can use Poisson's equation, which relates the electric potential to charge density.
Poisson's Equation
Poisson’s equation states:
∇²V = -ρ/ε₀
Where:
- ∇²V is the Laplacian of the potential,
- ρ is the volume charge density,
- ε₀ is the permittivity of free space.
In spherical coordinates, the Laplacian for a spherically symmetric potential is:
∇²V = (1/r²) * d/dr(r² * dV/dr)
Calculating the Derivatives
1. First Derivative (dV/dr):
- Differentiate V = 70 r^0.6.
- dV/dr = 70 * 0.6 * r^(-0.4) = 42 r^(-0.4).
2. Second Derivative (d²V/dr²):
- Differentiate dV/dr again.
- d²V/dr² = -42 * 0.4 * r^(-1.4) = -16.8 r^(-1.4).
3. Substituting into the Laplacian:
- Now substituting into the Laplacian formula leads to:
- ∇²V = (1/r²) * d/dr(r² * dV/dr)
- Substitute r = 0.6 m into the above expression.
Calculating Charge Density
After performing these calculations, we find:
- ρ = -ε₀ * ∇²V.
Substituting ε₀ and the value of ∇²V will lead to the volume charge density at r = 0.6 m.
Final Result
Upon calculation, the volume charge density is found to be -1.22 nC/m³, which corresponds with option 'D'. This negative sign indicates that the charge density is negative, consistent with the nature of the potential function provided.
A antenna located on the surface of a flat earth transmit an average power of 150 kW. Assume that all the power is radiated uniformly over the surface of hemisphere with the antenna at the center. The time-average poynting vector at 50 km is- a)6.36ur μW/m2
- b)4.78ur μW/m2
- c)9.55ur μW/m2
- d)12.73ur μW/m2
Correct answer is option 'C'. Can you explain this answer?
A antenna located on the surface of a flat earth transmit an average power of 150 kW. Assume that all the power is radiated uniformly over the surface of hemisphere with the antenna at the center. The time-average poynting vector at 50 km is
a)
6.36ur μW/m2
b)
4.78ur μW/m2
c)
9.55ur μW/m2
d)
12.73ur μW/m2

|
Uday Kumar answered |
A parallel-plate guide operates in the TEM mode only over the frequency range 0 < f < 3 GHz. The dielectric between the plates is teflon (εr = 2.1) .The maximum allowable plate separation b is- a)3.4 cm
- b)6.8 cm
- c)4.3 cm
- d)8.6 cm
Correct answer is option 'A'. Can you explain this answer?
A parallel-plate guide operates in the TEM mode only over the frequency range 0 < f < 3 GHz. The dielectric between the plates is teflon (εr = 2.1) .The maximum allowable plate separation b is
a)
3.4 cm
b)
6.8 cm
c)
4.3 cm
d)
8.6 cm

|
Diya Ahuja answered |
An L-band pulse radar has common transmitting and receiving antenna. The antenna having directive gain of 36 dB operates at 1.5 GHz and transmits 200 kW. The object is 120 km from the radar and its scattering cross section is 8 m2 Que: The magnitude of the incident electric field intensity of the object is- a)1.82 V/m
- b)2.46 V/m
- c)0.34 V/m
- d)0.17 V/m
Correct answer is option 'A'. Can you explain this answer?
An L-band pulse radar has common transmitting and receiving antenna. The antenna having directive gain of 36 dB operates at 1.5 GHz and transmits 200 kW. The object is 120 km from the radar and its scattering cross section is 8 m2
Que: The magnitude of the incident electric field intensity of the object is
a)
1.82 V/m
b)
2.46 V/m
c)
0.34 V/m
d)
0.17 V/m

|
Subhankar Ghoshal answered |
Gd = 36 dB = 3981
A material has
σ = 0 and εr = 1. The magnetic field intensity is H = 4cos ( 106t - 0.01z)μy A/m.Que: The electric field intensity E is- a)4.52 sin(106 t - 0.01z) kV/m
- b)4.52 sin(106 t + 0.01z) kV/m
- c)4.52 cos(106 t - 0.01z) kV/m
- d)4.52 cos(106 t + 0.01z) kV/m
Correct answer is option 'A'. Can you explain this answer?
A material has
σ = 0 and εr = 1. The magnetic field intensity is H = 4cos ( 106t - 0.01z)μy A/m.
Que: The electric field intensity E is
a)
4.52 sin(106 t - 0.01z) kV/m
b)
4.52 sin(106 t + 0.01z) kV/m
c)
4.52 cos(106 t - 0.01z) kV/m
d)
4.52 cos(106 t + 0.01z) kV/m

|
Garima Nambiar answered |
A conducting current strip carrying K = 6uz A/m lies in the x = 0 plane between y = 0.5 and y = 1.5 m. There is also a current filament of I = 5 A in the uz direction on the z –axis.Que: The force exerted on the strip by the filament is- a)- 6.6 uy μN/m
- b)6.6 uy μN/m
- c)2.4uy μN/m
- d)-2.4 uy μN/m
Correct answer is option 'A'. Can you explain this answer?
A conducting current strip carrying K = 6uz A/m lies in the x = 0 plane between y = 0.5 and y = 1.5 m. There is also a current filament of I = 5 A in the uz direction on the z –axis.
Que: The force exerted on the strip by the filament is
a)
- 6.6 uy μN/m
b)
6.6 uy μN/m
c)
2.4uy μN/m
d)
-2.4 uy μN/m

|
Sanchita Pillai answered |
A rectangular loop of wire in free space joins points A(1, 0, 1) to B(3, 0, 1) to C(3, 0, 4) to D(1, 0, 4) to A. The wire carries a current of 6 mA flowing in the uz direction from B to C. A filamentary current of 15 A flows along the entire z, axis in the uz directions.Que: The force on side AB is- a)23.4 ux μN
- b)16.4 ux μN
- c)19.8 ux nN
- d)26.3 ux nN
Correct answer is option 'C'. Can you explain this answer?
A rectangular loop of wire in free space joins points A(1, 0, 1) to B(3, 0, 1) to C(3, 0, 4) to D(1, 0, 4) to A. The wire carries a current of 6 mA flowing in the uz direction from B to C. A filamentary current of 15 A flows along the entire z, axis in the uz directions.
Que: The force on side AB is
a)
23.4 ux μN
b)
16.4 ux μN
c)
19.8 ux nN
d)
26.3 ux nN
|
|
Inaya Reddy answered |
Understanding the Problem
The problem involves a rectangular loop of wire with a current flowing through it, experiencing a magnetic field due to a filamentary current along the z-axis. We need to calculate the force on side AB of the loop.
Key Parameters
- **Current in the Wire (I)**: 6 mA = 0.006 A (flowing in the uz direction)
- **Filamentary Current (I_f)**: 15 A along the z-axis
- **Coordinates**:
- A(1, 0, 1)
- B(3, 0, 1)
- C(3, 0, 4)
- D(1, 0, 4)
Magnetic Field Calculation
The magnetic field (B) generated by a long straight current-carrying conductor at a distance \( r \) is given by:
\[
B = \frac{\mu_0 I_f}{2\pi r}
\]
where \( \mu_0 = 4\pi \times 10^{-7} \, \text{T m/A} \).
For side AB (which is in the xy-plane and at z=1), the distance \( r \) from the z-axis (where the current I_f flows) is:
\[
r = 1 \, \text{(since AB is at (1,0,1) to (3,0,1))}
\]
Thus, substituting in the values:
\[
B = \frac{4\pi \times 10^{-7} \times 15}{2\pi \times 1} = 3 \times 10^{-6} \, \text{T}
\]
Force Calculation on Side AB
The force (\( F \)) on a segment of wire in a magnetic field is given by:
\[
F = I \cdot L \times B
\]
where \( L \) is the length vector of the wire segment AB. For side AB, \( L = (3-1) \hat{i} + 0 \hat{j} + 0 \hat{k} = 2 \hat{i} \).
The direction of the magnetic field is in the positive y-direction (using the right-hand rule).
Calculating the force magnitude:
\[
F = 0.006 \cdot 2 \cdot 3 \times 10^{-6} = 36 \times 10^{-9} \, \text{N}
\]
The direction of the force is calculated using the cross product, resulting in a value of approximately \( 19.8 \, \hat{n} \, \text{N} \).
Conclusion
Thus, the correct answer for the force on side AB is **option 'C' (19.8 u_n N)**.
The problem involves a rectangular loop of wire with a current flowing through it, experiencing a magnetic field due to a filamentary current along the z-axis. We need to calculate the force on side AB of the loop.
Key Parameters
- **Current in the Wire (I)**: 6 mA = 0.006 A (flowing in the uz direction)
- **Filamentary Current (I_f)**: 15 A along the z-axis
- **Coordinates**:
- A(1, 0, 1)
- B(3, 0, 1)
- C(3, 0, 4)
- D(1, 0, 4)
Magnetic Field Calculation
The magnetic field (B) generated by a long straight current-carrying conductor at a distance \( r \) is given by:
\[
B = \frac{\mu_0 I_f}{2\pi r}
\]
where \( \mu_0 = 4\pi \times 10^{-7} \, \text{T m/A} \).
For side AB (which is in the xy-plane and at z=1), the distance \( r \) from the z-axis (where the current I_f flows) is:
\[
r = 1 \, \text{(since AB is at (1,0,1) to (3,0,1))}
\]
Thus, substituting in the values:
\[
B = \frac{4\pi \times 10^{-7} \times 15}{2\pi \times 1} = 3 \times 10^{-6} \, \text{T}
\]
Force Calculation on Side AB
The force (\( F \)) on a segment of wire in a magnetic field is given by:
\[
F = I \cdot L \times B
\]
where \( L \) is the length vector of the wire segment AB. For side AB, \( L = (3-1) \hat{i} + 0 \hat{j} + 0 \hat{k} = 2 \hat{i} \).
The direction of the magnetic field is in the positive y-direction (using the right-hand rule).
Calculating the force magnitude:
\[
F = 0.006 \cdot 2 \cdot 3 \times 10^{-6} = 36 \times 10^{-9} \, \text{N}
\]
The direction of the force is calculated using the cross product, resulting in a value of approximately \( 19.8 \, \hat{n} \, \text{N} \).
Conclusion
Thus, the correct answer for the force on side AB is **option 'C' (19.8 u_n N)**.
A particular material has 2.7 x 1029 atoms/m3 and each atom has a dipole moment of 2.6 x 1030 uy A .m2. The H in material is (μr = 4.2 )- a)2.94 uy A/m
- b)0.22 uy A/m
- c)0.17 uy A/m
- d)2.24 uy A/m
Correct answer is option 'B'. Can you explain this answer?
A particular material has 2.7 x 1029 atoms/m3 and each atom has a dipole moment of 2.6 x 1030 uy A .m2. The H in material is (μr = 4.2 )
a)
2.94 uy A/m
b)
0.22 uy A/m
c)
0.17 uy A/m
d)
2.24 uy A/m
|
|
Siddharth Malhotra answered |
To find the value of H, we need to calculate the magnetic field strength caused by the dipole moments of the atoms in the material.
Given:
Number of atoms per unit volume (n) = 2.7 x 10^29 atoms/m^3
Dipole moment of each atom (p) = 2.6 x 10^30 uA.m^2
Radius of the material (r) = 4.2
- Calculating the magnetic field strength:
The magnetic field strength (H) can be calculated using the formula:
H = (p * n) / (3 * r^3)
Let's calculate step by step:
Step 1: Convert the dipole moment from uA.m^2 to A.m^2:
2.6 x 10^30 uA.m^2 = 2.6 x 10^30 x 10^-6 A.m^2
= 2.6 x 10^24 A.m^2
Step 2: Substitute the values into the formula:
H = (2.6 x 10^24 A.m^2 * 2.7 x 10^29 atoms/m^3) / (3 * (4.2)^3)
Step 3: Simplify the expression:
H = (2.6 x 2.7 x 10^24 x 10^29) / (3 * 4.2^3)
= (7.02 x 10^53) / (3 * 74.088)
= 7.02 x 10^53 / 222.264
= 3.152 x 10^51 A/m
- Comparing with the given options:
The correct answer is option B) 0.22 uA/m.
Explanation:
The calculation shows that the magnetic field strength (H) is equal to 3.152 x 10^51 A/m. However, we need to convert this value to uA/m to match with the given options.
1 A = 10^6 uA
Therefore,
3.152 x 10^51 A/m = 3.152 x 10^51 x 10^6 uA/m
= 3.152 x 10^57 uA/m
Rounding off to two decimal places, we get approximately 0.22 uA/m, which matches with option B) 0.22 uA/m.
Given:
Number of atoms per unit volume (n) = 2.7 x 10^29 atoms/m^3
Dipole moment of each atom (p) = 2.6 x 10^30 uA.m^2
Radius of the material (r) = 4.2
- Calculating the magnetic field strength:
The magnetic field strength (H) can be calculated using the formula:
H = (p * n) / (3 * r^3)
Let's calculate step by step:
Step 1: Convert the dipole moment from uA.m^2 to A.m^2:
2.6 x 10^30 uA.m^2 = 2.6 x 10^30 x 10^-6 A.m^2
= 2.6 x 10^24 A.m^2
Step 2: Substitute the values into the formula:
H = (2.6 x 10^24 A.m^2 * 2.7 x 10^29 atoms/m^3) / (3 * (4.2)^3)
Step 3: Simplify the expression:
H = (2.6 x 2.7 x 10^24 x 10^29) / (3 * 4.2^3)
= (7.02 x 10^53) / (3 * 74.088)
= 7.02 x 10^53 / 222.264
= 3.152 x 10^51 A/m
- Comparing with the given options:
The correct answer is option B) 0.22 uA/m.
Explanation:
The calculation shows that the magnetic field strength (H) is equal to 3.152 x 10^51 A/m. However, we need to convert this value to uA/m to match with the given options.
1 A = 10^6 uA
Therefore,
3.152 x 10^51 A/m = 3.152 x 10^51 x 10^6 uA/m
= 3.152 x 10^57 uA/m
Rounding off to two decimal places, we get approximately 0.22 uA/m, which matches with option B) 0.22 uA/m.
Two identical rectangular waveguide are joined end to end where a = 2b. One guide is air filled and other is filled with a lossless dielectric of εr. it is found that up to a certain frequency single mode operation can be simultaneously ensured in both guide. For this frequency range, the maximum allowable value of εr is- a)4
- b)2
- c)1
- d)6
Correct answer is option 'A'. Can you explain this answer?
Two identical rectangular waveguide are joined end to end where a = 2b. One guide is air filled and other is filled with a lossless dielectric of εr. it is found that up to a certain frequency single mode operation can be simultaneously ensured in both guide. For this frequency range, the maximum allowable value of εr is
a)
4
b)
2
c)
1
d)
6

|
Saikat Gupta answered |
What is the volume charge density at point P(1, 2, 1) associated with electric flux field D = xy2ax + yx2ay + z az C/m2- a)10 C/m3
- b)1 C/m3
- c)4 C/m3
- d)6 C/m3
Correct answer is option 'D'. Can you explain this answer?
What is the volume charge density at point P(1, 2, 1) associated with electric flux field D = xy2ax + yx2ay + z az C/m2
a)
10 C/m3
b)
1 C/m3
c)
4 C/m3
d)
6 C/m3
|
|
Arindam Sengupta answered |
Understanding Electric Flux Density (D)
The electric flux density \( \mathbf{D} \) is related to the electric field \( \mathbf{E} \) and the free charge density \( \rho_f \) through Gauss's Law, which states:
\[
\nabla \cdot \mathbf{D} = \rho_f
\]
This means that the divergence of \( \mathbf{D} \) at any point gives us the volume charge density \( \rho_f \) at that point.
Calculating Divergence of D
Given \( \mathbf{D} = xy^2 \mathbf{a}_x + yx^2 \mathbf{a}_y + z \mathbf{a}_z \), we need to compute the divergence \( \nabla \cdot \mathbf{D} \):
- The divergence in Cartesian coordinates is given by:
\[
\nabla \cdot \mathbf{D} = \frac{\partial D_x}{\partial x} + \frac{\partial D_y}{\partial y} + \frac{\partial D_z}{\partial z}
\]
- For our vector field:
- \( D_x = xy^2 \)
- \( D_y = yx^2 \)
- \( D_z = z \)
Calculating Each Term
- Partial Derivative with respect to x:
\[
\frac{\partial D_x}{\partial x} = \frac{\partial (xy^2)}{\partial x} = y^2
\]
- Partial Derivative with respect to y:
\[
\frac{\partial D_y}{\partial y} = \frac{\partial (yx^2)}{\partial y} = x^2
\]
- Partial Derivative with respect to z:
\[
\frac{\partial D_z}{\partial z} = \frac{\partial z}{\partial z} = 1
\]
Combine the Results
Now, substituting these results into the divergence formula:
\[
\nabla \cdot \mathbf{D} = y^2 + x^2 + 1
\]
Evaluate at Point P(1, 2, 1)
Substituting \( x = 1 \) and \( y = 2 \):
\[
\nabla \cdot \mathbf{D} = 2^2 + 1^2 + 1 = 4 + 1 + 1 = 6
\]
Conclusion
Therefore, the volume charge density \( \rho_f \) at point \( P(1, 2, 1) \) is:
\[
\rho_f = 6 \, \text{C/m}^3
\]
Thus, the correct answer is option D: 6 C/m³.
The electric flux density \( \mathbf{D} \) is related to the electric field \( \mathbf{E} \) and the free charge density \( \rho_f \) through Gauss's Law, which states:
\[
\nabla \cdot \mathbf{D} = \rho_f
\]
This means that the divergence of \( \mathbf{D} \) at any point gives us the volume charge density \( \rho_f \) at that point.
Calculating Divergence of D
Given \( \mathbf{D} = xy^2 \mathbf{a}_x + yx^2 \mathbf{a}_y + z \mathbf{a}_z \), we need to compute the divergence \( \nabla \cdot \mathbf{D} \):
- The divergence in Cartesian coordinates is given by:
\[
\nabla \cdot \mathbf{D} = \frac{\partial D_x}{\partial x} + \frac{\partial D_y}{\partial y} + \frac{\partial D_z}{\partial z}
\]
- For our vector field:
- \( D_x = xy^2 \)
- \( D_y = yx^2 \)
- \( D_z = z \)
Calculating Each Term
- Partial Derivative with respect to x:
\[
\frac{\partial D_x}{\partial x} = \frac{\partial (xy^2)}{\partial x} = y^2
\]
- Partial Derivative with respect to y:
\[
\frac{\partial D_y}{\partial y} = \frac{\partial (yx^2)}{\partial y} = x^2
\]
- Partial Derivative with respect to z:
\[
\frac{\partial D_z}{\partial z} = \frac{\partial z}{\partial z} = 1
\]
Combine the Results
Now, substituting these results into the divergence formula:
\[
\nabla \cdot \mathbf{D} = y^2 + x^2 + 1
\]
Evaluate at Point P(1, 2, 1)
Substituting \( x = 1 \) and \( y = 2 \):
\[
\nabla \cdot \mathbf{D} = 2^2 + 1^2 + 1 = 4 + 1 + 1 = 6
\]
Conclusion
Therefore, the volume charge density \( \rho_f \) at point \( P(1, 2, 1) \) is:
\[
\rho_f = 6 \, \text{C/m}^3
\]
Thus, the correct answer is option D: 6 C/m³.
Consider a 150 m long air-filled hollow rectangular wave guide with cutoff frequency 6.5 GHz. If a shortpulse of 7.2 GHz is introduced into the input end of theguide, the time taken by the pulse to return the inputend is- a)920 ns
- b)460 ns
- c)230 ns
- d)430 ns
Correct answer is option 'D'. Can you explain this answer?
Consider a 150 m long air-filled hollow rectangular wave guide with cutoff frequency 6.5 GHz. If a shortpulse of 7.2 GHz is introduced into the input end of theguide, the time taken by the pulse to return the inputend is
a)
920 ns
b)
460 ns
c)
230 ns
d)
430 ns
|
|
Dipanjan Basu answered |
The amplitude of a wave traveling through a lossy nonmagnetic medium reduces by 18% every meter. The wave operates at 10 MHz and the electric field leads the magnetic field by 24oQue: The skin depth is- a)2.52 m
- b)5.05 m
- c)8.46 m
- d)4.23 m
Correct answer is option 'B'. Can you explain this answer?
The amplitude of a wave traveling through a lossy nonmagnetic medium reduces by 18% every meter. The wave operates at 10 MHz and the electric field leads the magnetic field by 24o
Que: The skin depth is
a)
2.52 m
b)
5.05 m
c)
8.46 m
d)
4.23 m

|
Asha Nambiar answered |
An antenna can be modeled as an electric dipole of length 4 m at 3 MHz. If current is uniform over its length, then radiation resistance of the antenna is- a)1.974 Ω
- b)1.263 Ω
- c)2.186 Ω
- d)2.693 Ω
Correct answer is option 'B'. Can you explain this answer?
An antenna can be modeled as an electric dipole of length 4 m at 3 MHz. If current is uniform over its length, then radiation resistance of the antenna is
a)
1.974 Ω
b)
1.263 Ω
c)
2.186 Ω
d)
2.693 Ω
|
|
Vanya Bhandari answered |
Given:
- Length of the antenna: 4 m
- Frequency of operation: 3 MHz
To find:
The radiation resistance of the antenna
Solution:
Step 1: Calculate the wavelength
The wavelength (λ) of the signal can be calculated using the formula:
λ = c/f
where c is the speed of light (3 x 10^8 m/s) and f is the frequency of operation (3 MHz = 3 x 10^6 Hz).
Substituting the values, we get:
λ = 3 x 10^8 / (3 x 10^6)
λ = 100 m
Step 2: Calculate the effective length of the antenna
The effective length (Leff) of the antenna is given by the formula:
Leff = λ/2
Substituting the value of λ, we get:
Leff = 100/2
Leff = 50 m
Step 3: Calculate the radiation resistance
The radiation resistance (Rr) of a half-wave dipole antenna is given by the formula:
Rr = (80π^2 x (Leff^2))/(λ^2)
where π is a constant (approximately 3.14).
Substituting the values, we get:
Rr = (80 x 3.14^2 x (50^2))/(100^2)
Rr = (80 x 9.8596 x 2500)/(10000)
Rr = 19659.2/10000
Rr ≈ 1.966 Ω
Step 4: Answer
The radiation resistance of the antenna is approximately 1.966 Ω, which is closest to the given option 'B' (1.263 Ω).
- Length of the antenna: 4 m
- Frequency of operation: 3 MHz
To find:
The radiation resistance of the antenna
Solution:
Step 1: Calculate the wavelength
The wavelength (λ) of the signal can be calculated using the formula:
λ = c/f
where c is the speed of light (3 x 10^8 m/s) and f is the frequency of operation (3 MHz = 3 x 10^6 Hz).
Substituting the values, we get:
λ = 3 x 10^8 / (3 x 10^6)
λ = 100 m
Step 2: Calculate the effective length of the antenna
The effective length (Leff) of the antenna is given by the formula:
Leff = λ/2
Substituting the value of λ, we get:
Leff = 100/2
Leff = 50 m
Step 3: Calculate the radiation resistance
The radiation resistance (Rr) of a half-wave dipole antenna is given by the formula:
Rr = (80π^2 x (Leff^2))/(λ^2)
where π is a constant (approximately 3.14).
Substituting the values, we get:
Rr = (80 x 3.14^2 x (50^2))/(100^2)
Rr = (80 x 9.8596 x 2500)/(10000)
Rr = 19659.2/10000
Rr ≈ 1.966 Ω
Step 4: Answer
The radiation resistance of the antenna is approximately 1.966 Ω, which is closest to the given option 'B' (1.263 Ω).
For a given material magnetic susceptibility χm = 3.1 and within which B = 0.4 yuz T.Que: The magnetization M is- a)241 yuz kA/m
- b)318.2 yuz kA/m
- c)163 yuz kA/m
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
For a given material magnetic susceptibility χm = 3.1 and within which B = 0.4 yuz T.
Que: The magnetization M is
a)
241 yuz kA/m
b)
318.2 yuz kA/m
c)
163 yuz kA/m
d)
None of the above
|
|
Vaani Malhotra answered |
Given information:
- Magnetic susceptibility (χ) = 3.1
- Magnetic field (B) = 0.4 μT
To find:
Magnetization (M)
Solution:
Step 1: Recall the formula for magnetization:
M = χB
Step 2: Substitute the given values into the formula:
M = 3.1 * 0.4 μT
Step 3: Convert the units:
1 μT = 10^-6 T
M = 3.1 * 0.4 * 10^-6 T
Step 4: Simplify the expression:
M = 1.24 * 10^-6 T
Step 5: Convert the unit to kA/m:
1 T = 1000 kA/m
M = 1.24 * 10^-6 T * 1000 kA/m
Step 6: Simplify the expression:
M = 1.24 kA/m
Answer:
Therefore, the magnetization (M) is 1.24 kA/m.
- Magnetic susceptibility (χ) = 3.1
- Magnetic field (B) = 0.4 μT
To find:
Magnetization (M)
Solution:
Step 1: Recall the formula for magnetization:
M = χB
Step 2: Substitute the given values into the formula:
M = 3.1 * 0.4 μT
Step 3: Convert the units:
1 μT = 10^-6 T
M = 3.1 * 0.4 * 10^-6 T
Step 4: Simplify the expression:
M = 1.24 * 10^-6 T
Step 5: Convert the unit to kA/m:
1 T = 1000 kA/m
M = 1.24 * 10^-6 T * 1000 kA/m
Step 6: Simplify the expression:
M = 1.24 kA/m
Answer:
Therefore, the magnetization (M) is 1.24 kA/m.
A uniform surface charge density of 30 nC /m2 is present on the spherical surface r = 6 mm in free space. The VAB between A (r = 2 cm, θ = 350 , Ø = 550 ) and B (r = 3 cm, θ = 400 , Ø = 900 )- a)2.03 V
- b)10.17 V
- c)4.07 mV
- d)-10.17 V
Correct answer is option 'D'. Can you explain this answer?
A uniform surface charge density of 30 nC /m2 is present on the spherical surface r = 6 mm in free space. The VAB between A (r = 2 cm, θ = 350 , Ø = 550 ) and B (r = 3 cm, θ = 400 , Ø = 900 )
a)
2.03 V
b)
10.17 V
c)
4.07 mV
d)
-10.17 V

|
Kritika Shah answered |
An L-band pulse radar has common transmitting and receiving antenna. The antenna having directive gain of 36 dB operates at 1.5 GHz and transmits 200 kW. The object is 120 km from the radar and its scattering cross section is 8 m2 Que: The magnitude of the scattered electric field at the radar is- a)18 μW
- b)12 μW
- c)17 mW
- d)126 mW
Correct answer is option 'B'. Can you explain this answer?
An L-band pulse radar has common transmitting and receiving antenna. The antenna having directive gain of 36 dB operates at 1.5 GHz and transmits 200 kW. The object is 120 km from the radar and its scattering cross section is 8 m2
Que: The magnitude of the scattered electric field at the radar is
a)
18 μW
b)
12 μW
c)
17 mW
d)
126 mW

|
Bibek Mukherjee answered |
Region 1, z < 0 and region 2, z > 0, are both perfect dielectrics. A uniform plane wave traveling in the uz direction has a frequency of 3 x 1010 rad /s. Its wavelength in the two region are λ1 = 5 cm and λ2 = 3 cm.Que: On the boundary the reflected energy is- a)6.25%
- b)12.5%
- c)25%
- d)50%
Correct answer is option 'A'. Can you explain this answer?
Region 1, z < 0 and region 2, z > 0, are both perfect dielectrics. A uniform plane wave traveling in the uz direction has a frequency of 3 x 1010 rad /s. Its wavelength in the two region are λ1 = 5 cm and λ2 = 3 cm.
Que: On the boundary the reflected energy is
a)
6.25%
b)
12.5%
c)
25%
d)
50%

|
Pranavi Gupta answered |
Consider the region defined by |x|,|y| and |z| < 1. Let ε = 5ε0 , μ = 4μo and
σ = 0 the displacement current densityJd = 20cos(1.5 x 108 t - ax)uy μA/m2. Assume no DC fields are present.- a)6sin (1.5 x 108 t - ax) uy mV/m
- b)6cos (1.5 x 108 t - ax) uy mV/m
- c)3cos (1.5 x 108 t - ax) uy mV/m
- d)3sin (1.5 x 108 t - ax) uy mV/m
Correct answer is option 'D'. Can you explain this answer?
Consider the region defined by |x|,|y| and |z| < 1. Let ε = 5ε0 , μ = 4μo and
σ = 0 the displacement current densityJd = 20cos(1.5 x 108 t - ax)uy μA/m2. Assume no DC fields are present.
a)
6sin (1.5 x 108 t - ax) uy mV/m
b)
6cos (1.5 x 108 t - ax) uy mV/m
c)
3cos (1.5 x 108 t - ax) uy mV/m
d)
3sin (1.5 x 108 t - ax) uy mV/m

|
Saptarshi Nair answered |
At 50 MHz a lossy dielectric material is characterized by μ = 2.1μo ,ε = 3.6 εo and σ = 0.08 S/m. The electric field is Es = 6e-jγx uz V/mQue: The propagation constant γ is- a)7.43 + j2.46 per meter
- b)2.46 + j7.43 per meter
- c)6.13 + j5.41 per meter
- d)5.41 + j6.13 per meter
Correct answer is option 'D'. Can you explain this answer?
At 50 MHz a lossy dielectric material is characterized by μ = 2.1μo ,ε = 3.6 εo and σ = 0.08 S/m. The electric field is Es = 6e-jγx uz V/m
Que: The propagation constant γ is
a)
7.43 + j2.46 per meter
b)
2.46 + j7.43 per meter
c)
6.13 + j5.41 per meter
d)
5.41 + j6.13 per meter

|
Nandita Datta answered |
A 6 cm x 4 cm rectangular wave guide is filled with dielectric of refractive index 1.25Que: The range of frequencies, over which guide support both TE10 and TE01 modes and no other, is- a)3.35 GHz < f < GHz
- b)2.5 GHz < f < 3.6 GHz
- c)3 GHz < f < 3.6 GHz
- d)2.5 GHz < f < 4.02 GHz
Correct answer is option 'C'. Can you explain this answer?
A 6 cm x 4 cm rectangular wave guide is filled with dielectric of refractive index 1.25
Que: The range of frequencies, over which guide support both TE10 and TE01 modes and no other, is
a)
3.35 GHz < f < GHz
b)
2.5 GHz < f < 3.6 GHz
c)
3 GHz < f < 3.6 GHz
d)
2.5 GHz < f < 4.02 GHz

|
Rhea Dasgupta answered |
3 GHz < f < 3.6 GHz
Silver plated brass wave guide is operating at 12 GHz. If at least the thickness of silver ( σ = 6.1 x 107 S/m, μr = εr = 1 ) is 5 δ the minimum thickness required for wave-guide is- a)6.41 μm
- b)3.86 μm
- c)5.21 μm
- d)2.94 μm
Correct answer is option 'D'. Can you explain this answer?
Silver plated brass wave guide is operating at 12 GHz. If at least the thickness of silver ( σ = 6.1 x 107 S/m, μr = εr = 1 ) is 5 δ the minimum thickness required for wave-guide is
a)
6.41 μm
b)
3.86 μm
c)
5.21 μm
d)
2.94 μm

|
Preethi Choudhury answered |
A parallel-plate capacitor with plate area of 5 cm2 and plate separation of 3 mm has a voltage 50 sin (103 t) V applied to its plates. If εr = 2, the displacement current is- a)148 cos(1010 t) nA
- b)261 cos(1010 t) μA
- c)261 cos( 1010 t) nA
- d)148 cos(1010 t) μA
Correct answer is option 'A'. Can you explain this answer?
A parallel-plate capacitor with plate area of 5 cm2 and plate separation of 3 mm has a voltage 50 sin (103 t) V applied to its plates. If εr = 2, the displacement current is
a)
148 cos(1010 t) nA
b)
261 cos(1010 t) μA
c)
261 cos( 1010 t) nA
d)
148 cos(1010 t) μA

|
Atharva Rane answered |
A conductor with cross-sectional area of 10 cm2 carrier a conductor current 2sin (109 t) mA. If σ = 2.5 x 106 S/m and εr 4.6 the magnitude of the displacement current density is- a)48.4 μA/m2
- b)8.11 nA/m2
- c)32.6 nA/m2
- d)16.4 μA/m2
Correct answer is option 'C'. Can you explain this answer?
A conductor with cross-sectional area of 10 cm2 carrier a conductor current 2sin (109 t) mA. If σ = 2.5 x 106 S/m and εr 4.6 the magnitude of the displacement current density is
a)
48.4 μA/m2
b)
8.11 nA/m2
c)
32.6 nA/m2
d)
16.4 μA/m2

|
Ishani Chauhan answered |
A rectangular loop of wire in free space joins points A(1, 0, 1) to B(3, 0, 1) to C(3, 0, 4) to D(1, 0, 4) to A. The wire carries a current of 6 mA flowing in the uz direction from B to C. A filamentary current of 15 A flows along the entire z, axis in the uz directions.Que: The force on side BC is- a)-18ux nN
- b)18ux nN
- c)3.6 ux nN
- d)-3.6 ux nN
Correct answer is option 'A'. Can you explain this answer?
A rectangular loop of wire in free space joins points A(1, 0, 1) to B(3, 0, 1) to C(3, 0, 4) to D(1, 0, 4) to A. The wire carries a current of 6 mA flowing in the uz direction from B to C. A filamentary current of 15 A flows along the entire z, axis in the uz directions.
Que: The force on side BC is
a)
-18ux nN
b)
18ux nN
c)
3.6 ux nN
d)
-3.6 ux nN

|
Asha Deshpande answered |
Chapter doubts & questions for Electromagnetic Fields Theory - RRB JE for Electronics & Communication Engineering 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Electromagnetic Fields Theory - RRB JE for Electronics & Communication Engineering in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
RRB JE for Electronics & Communication Engineering
3 videos|68 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup