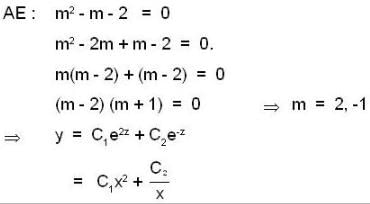All Exams >
Mathematics >
IIT JAM Mathematics Mock Test Series >
All Questions
All questions of Practice Test for IIT Jam Mathematics for Mathematics Exam
A group (G, *) has 10 elements. The minimum number of elements of G, which are their own inverse is- a)2
- b)1
- c)9
- d)0
Correct answer is option 'B'. Can you explain this answer?
A group (G, *) has 10 elements. The minimum number of elements of G, which are their own inverse is
a)
2
b)
1
c)
9
d)
0
|
|
Chirag Verma answered |
Since,in a group there must be an identity element.Also it is its own inverse. Therefore,minimum number of elements of G,which are their own inverse=1
Find the number of element of order 10 in Z30‘
Correct answer is '4'. Can you explain this answer?
Find the number of element of order 10 in Z30‘
|
|
Chirag Verma answered |
Since, the number of elements of order cl in a cyclic group of order n is φ(d), where d is positive divisor of n. Hence, the number of elements of order 10 in 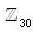 is
is
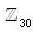 is
is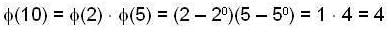
The system of linear equations(4d - 1) x + y + z = 0, - y + z = 0, (4d - 1 )z = 0 has a non-trivial solution, if the value of d is ___ .
Correct answer is '0.25'. Can you explain this answer?
The system of linear equations
(4d - 1) x + y + z = 0, - y + z = 0, (4d - 1 )z = 0 has a non-trivial solution, if the value of d is ___ .
|
|
Chirag Verma answered |
The system of homogeneous linear equations has a non-trivial solution, if
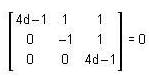

Find the directional derivative of φ = x2yz + 4xz2 at (1, - 2 , - 1 ) in the direction 2i - j - 2k.
Correct answer is '12.34'. Can you explain this answer?
Find the directional derivative of φ = x2yz + 4xz2 at (1, - 2 , - 1 ) in the direction 2i - j - 2k.
|
|
Chirag Verma answered |

The unit vector in the direction of 2i - j - 2k is
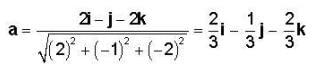
Then the required directional derivative is
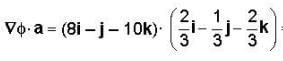
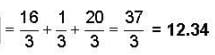
Since this is positive,increasing in this direction.
Which one is a group under multiplication modulo 11?- a){1,8}
- b){9,1}
- c){10,1}
- d){1,3,5,7,8}
Correct answer is option 'C'. Can you explain this answer?
Which one is a group under multiplication modulo 11?
a)
{1,8}
b)
{9,1}
c)
{10,1}
d)
{1,3,5,7,8}
|
|
Chirag Verma answered |
By the definition of operation table of a group.


Which of the following is correct?- a)Every subgroup of an abelian group is normal
- b)Every subgroup of a cyclic group is normal
- c)Intersection of any two normal subgroup is a normal subgroup
- d)If N is a normal subgroup of G and H is any subgroup of G then NH is normal subgroup of G.
Correct answer is option 'A,B,C'. Can you explain this answer?
Which of the following is correct?
a)
Every subgroup of an abelian group is normal
b)
Every subgroup of a cyclic group is normal
c)
Intersection of any two normal subgroup is a normal subgroup
d)
If N is a normal subgroup of G and H is any subgroup of G then NH is normal subgroup of G.
|
|
Chirag Verma answered |
Every subgroup of an abelian group is normal as for every x ∈ G and h ∈ H
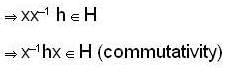
Every subgroup of cyclic group is normal and intersection of two normal subgroups is normal subgroup again.
If N is a normal subgroup of G and H is any subgroup of G then NH is a subgroup of G but NH is necessarily not normal.
If N is a normal subgroup of G and H is any subgroup of G then NH is a subgroup of G but NH is necessarily not normal.
___________ is the order of {3} in the multiplicative group of integers modulo 5.
Correct answer is '4'. Can you explain this answer?
___________ is the order of {3} in the multiplicative group of integers modulo 5.
|
|
Chirag Verma answered |
The identity of the multiplicative group of integers modulo 5 is {1}.
Here
{3}.5{3} = 4 * {1} [•, 3.3 0 4 (mod 5)]
∴ {3}.5{3}.5{3} = {4}.5{3} = {2} * {1} [∵, 4.30 2 (mod 5)]
∴{3}.5{3}.5{3}.5{3} = {2}.5{3} = {1} [∵, 2.30 (mod 5)]
Hence, the order of {3} is 4.
Let {un} be a sequence of real number's. If ∑|un| is convergent series. Then which of the following's is/are true?- a)
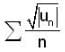 is convergent
is convergent - b)
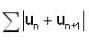 divergent
divergent - c)
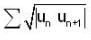 is convergent
is convergent - d)
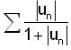 is convergent
is convergent
Correct answer is option 'A,C,D'. Can you explain this answer?
Let {un} be a sequence of real number's. If ∑|un| is convergent series. Then which of the following's is/are true?
a)
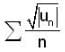 is convergent
is convergent b)
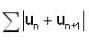 divergent
divergentc)
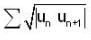 is convergent
is convergent d)
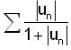 is convergent
is convergent |
|
Chirag Verma answered |
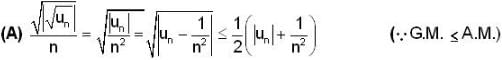
Now given ∑|un| Convergent and we know ∑1/n2 is convergent so by comparison test
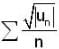 is Convergent.
is Convergent.
Let G be a group of order 143, then the centre of G is isomorphic to- a)Z
- b)Z11
- c)Z13
- d)Z143
Correct answer is option 'D'. Can you explain this answer?
Let G be a group of order 143, then the centre of G is isomorphic to
a)
Z
b)
Z11
c)
Z13
d)
Z143
|
|
Chirag Verma answered |
O(G) = 143
i.e. O(G) =11 x 13 (p < q)
Here.O(G) = pq , p < q and p X q -1, so G be a cyclic group of order 143 and every cyclic group is an abelian group.
Hence G is an abelian group, if G be an abelian group then centre of G is equal to group G.
G = Z(G) [∵ G is an abelian]
i.e. O[Z(G)] = 143 so Z(G) is isomorphic to Z143.
i.e. O(G) =11 x 13 (p < q)
Here.O(G) = pq , p < q and p X q -1, so G be a cyclic group of order 143 and every cyclic group is an abelian group.
Hence G is an abelian group, if G be an abelian group then centre of G is equal to group G.
G = Z(G) [∵ G is an abelian]
i.e. O[Z(G)] = 143 so Z(G) is isomorphic to Z143.
If G is a group, Z its center and if G/Z is cyclic then G- a)must be abelian
- b)must be non abelian
- c)must be normal subgroup
- d)must be subgroup
Correct answer is option 'A'. Can you explain this answer?
If G is a group, Z its center and if G/Z is cyclic then G
a)
must be abelian
b)
must be non abelian
c)
must be normal subgroup
d)
must be subgroup
|
|
Chirag Verma answered |
We have given that G/Z is a cyclic group, so let Zg is a generator of the cyclic group G/Z, where g ∈ G.
W e now show that G is an abelian group i.e.,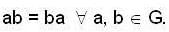
Since a ∈ G, so Za ∈ G/Z. But G/Z is a cyclic group which is gen era ted by Zg. Thus there exists an integer m such that
W e now show that G is an abelian group i.e.,
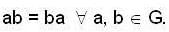
Since a ∈ G, so Za ∈ G/Z. But G/Z is a cyclic group which is gen era ted by Zg. Thus there exists an integer m such that
Za = (Zg)m = Zgm [∵ Z is a normal subgroup of G]
Again
a ∈ Za and Za = Zgm ⇒ a ∈ Z gm.
Now
a ∈ Z g m ⇒  z1 ∈ Z such that a ∈ z1 gm
z1 ∈ Z such that a ∈ z1 gm
 z1 ∈ Z such that a ∈ z1 gm
z1 ∈ Z such that a ∈ z1 gmSimilarly, for b ∈ G, b = z2 gn, where z2 ∈ z and n is any integer.
Now
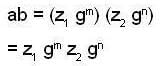
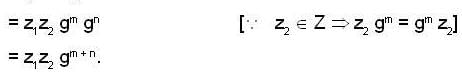 Again
Again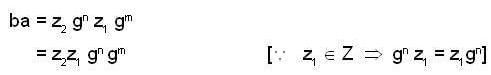
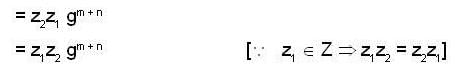
Let GL(2, Z5) is a group for multiplication of matrix operation such that ad - be ≠ 0 then order of the group GL(2,Z5) is
Correct answer is '480'. Can you explain this answer?
Let GL(2, Z5) is a group for multiplication of matrix operation such that ad - be ≠ 0 then order of the group GL(2,Z5) is
|
|
Chirag Verma answered |
We know that the order of general linear group GL(n, Zp) is
= (Pn-1) (Pn - P) (Pn - P2)_____ (Pn - Pn-1)
Here P = 5 , n = 2
0[GL(2,Z5)] = (52 - 1) (52 - 5)
= 24 x 20
= 480
= (Pn-1) (Pn - P) (Pn - P2)_____ (Pn - Pn-1)
Here P = 5 , n = 2
0[GL(2,Z5)] = (52 - 1) (52 - 5)
= 24 x 20
= 480
Find the total number of cyclic subgroups of order 10 in 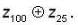
Correct answer is '6'. Can you explain this answer?
Find the total number of cyclic subgroups of order 10 in 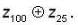
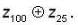

|
Veda Institute answered |
Case - I
|a|= 10 and|b| = 1 or 5. since z100 has a unique cyclic subgroup of order 10 and cyclic group of order 10 has four generators, i.e. there are four choices for a Similarly, there are five choices for b. This gives 20 possibilities for (a,b).
Case - II lal = 2 and|b| = 5 .
Since any finite cyclic group of even order has a unique subgroup of order 2, there is only one choice for a.
So, obviously there are four choices for b.
Hence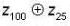 has 24 elements of order 10. Because each cyclic subgroup of order 10 has four elements of order 10 and no two of the cyclic subgroups can have an element of order 10 in common. There must be 24/4 = 6 cyclic subgroups of order 10.
has 24 elements of order 10. Because each cyclic subgroup of order 10 has four elements of order 10 and no two of the cyclic subgroups can have an element of order 10 in common. There must be 24/4 = 6 cyclic subgroups of order 10.
|a|= 10 and|b| = 1 or 5. since z100 has a unique cyclic subgroup of order 10 and cyclic group of order 10 has four generators, i.e. there are four choices for a Similarly, there are five choices for b. This gives 20 possibilities for (a,b).
Case - II lal = 2 and|b| = 5 .
Since any finite cyclic group of even order has a unique subgroup of order 2, there is only one choice for a.
So, obviously there are four choices for b.
Hence
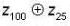 has 24 elements of order 10. Because each cyclic subgroup of order 10 has four elements of order 10 and no two of the cyclic subgroups can have an element of order 10 in common. There must be 24/4 = 6 cyclic subgroups of order 10.
has 24 elements of order 10. Because each cyclic subgroup of order 10 has four elements of order 10 and no two of the cyclic subgroups can have an element of order 10 in common. There must be 24/4 = 6 cyclic subgroups of order 10.Find the length of the arc of the semi cubical parabola ay2 = x3 from its vertex to the point (a, a).- a)
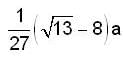
- b)
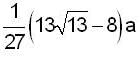
- c)
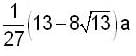
- d)
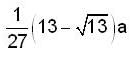
Correct answer is option 'B'. Can you explain this answer?
Find the length of the arc of the semi cubical parabola ay2 = x3 from its vertex to the point (a, a).
a)
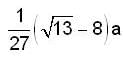
b)
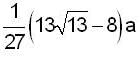
c)
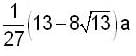
d)
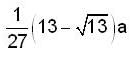

|
Veda Institute answered |
Differentiating the equation of the curve
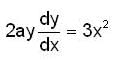
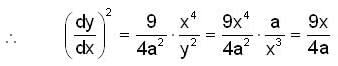
Therefore the required length
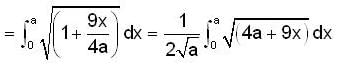

Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is ______.
Correct answer is '7'. Can you explain this answer?
Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is ______.
|
|
Chirag Verma answered |
Group G has 35 elements, i.e. its order is 35
So, possible subgroup sizes can be 1, 5, 7, 35.
Thus the largest possible size of subgroup other than G itself (proper subgroup) is 7.
Let T = { z ∈ c : | z | = 1} then (T, x) is a group which o f the following are not subgroup of (T, x)- a)({1, -1, i, -i}, x)
- b)({1.-1}. X)
- c)
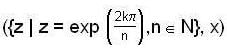
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Let T = { z ∈ c : | z | = 1} then (T, x) is a group which o f the following are not subgroup of (T, x)
a)
({1, -1, i, -i}, x)
b)
({1.-1}. X)
c)
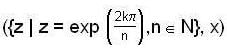
d)
None of these
|
|
Mister Genius answered |
If T = {z ∈ s c : | z | = 1} then (T, x) is said to be a circle group All though the circle group has infinite order it has many finite subgroups as the complex numbers satisfying the equation zn = 1 are called the nth root of unity. They are
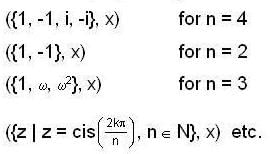
Which one of the following is a group?- a)(N, *) where a * b = a for all a, b ∈ N
- b)(Z, *) where a + b = a - b for all a, b ∈ Z
- c)(Q, *) where a * b = ab/2 for all a, b ∈ Q
- d)(R, *) where a + b = a + b + 1 for all a, b ∈ R
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is a group?
a)
(N, *) where a * b = a for all a, b ∈ N
b)
(Z, *) where a + b = a - b for all a, b ∈ Z
c)
(Q, *) where a * b = ab/2 for all a, b ∈ Q
d)
(R, *) where a + b = a + b + 1 for all a, b ∈ R
|
|
Chirag Verma answered |
(N, *) where 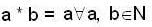
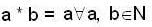
closure property a* b = a ∈ N
Associativity (a * b) * c = a * c = a
a * (b * c) = a * b = a
a * (b * c) = a * b = a
identity
a * e = a
a = a
⇒ there does not exist identity
⇒ (N, *) is not a group.
(B) (Z, *) where a * b = a - b for all a, b ∈Z (Z, *) is a group if all four properties of the group are satisfied. These properties are
(1) Closure property : If a, b ∈ Z, then a * b = a - b∈Z => closure property is satisfied
(2) Associativity => If a, b, c ∈ Z, then (a * b) * c = (a - b) * c = a - b - c ...(i)
and a*(b*c) = a * ( b - c ) = a - ( b - c ) = a - b + c ...(ii)
Hence by Eqs. (i) and (ii) (a * b) * c≠a*(b*c)
Hence the property of associativity is not satisfied.
=> (Z, *) is not a group.
(C) (Q, *) where 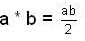 for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.
for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.
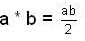 for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.
for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.For; identity => let identity is e, then a * e = a, let a ≠ o .
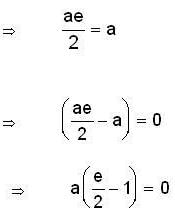
⇒ if a ≠ 0 then e = 2, Thus if a = 0 then e cannot be 2
⇒ inverse of a = 0 does not exist. Hence it is not a group
(D) (R, *) w here a * b = a + b + 1 ,a , b ∈ R This is a g roup with identity given as a *
e = a + e +1 = a
⇒ a + e + 1 = a
⇒ e + 1 = a - a
⇒ e + 1 =0
⇒ e = - 1
Since - 1 ∈ Q, so e ∈ Q, So (R, *) is a group with identity - 1 .
If f(x) = (x2 - 1) |x2 - 3x + 2| + cos|x| then the set of point of non-differentiability is,- a){1,0,2}
- b){1,2}
- c){2}
- d){0,2}
Correct answer is option 'C'. Can you explain this answer?
If f(x) = (x2 - 1) |x2 - 3x + 2| + cos|x| then the set of point of non-differentiability is,
a)
{1,0,2}
b)
{1,2}
c)
{2}
d)
{0,2}

|
Veda Institute answered |
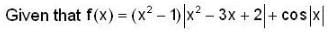
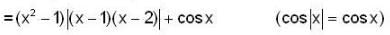
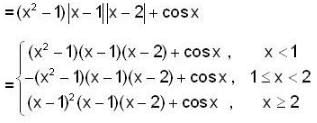
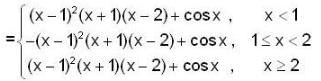
Clearly the rule of the function is changing of x = 1 and 2.
So we shall test the differentiability of f(x) only at the points x = 1 and x = 2.
clearly Rf '(1) - Lf'(1)
and Rf*(2) ≠ Lf'(2)
hence f(x) is not differentiable at x = 2.
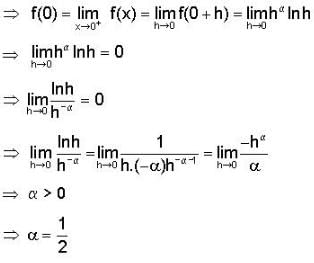
If f(x) = xα In x and f(0) = 0, then the value of α for which Rolle’s theorem can be applied in [0,1] is,- a)-2
- b)-1
- c)0
- d)1/2
Correct answer is option 'D'. Can you explain this answer?
If f(x) = xα In x and f(0) = 0, then the value of α for which Rolle’s theorem can be applied in [0,1] is,
a)
-2
b)
-1
c)
0
d)
1/2
|
|
Chirag Verma answered |
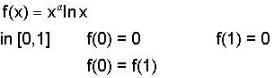
The function has to be continuous in [0,1]
Number of generators of group Z16- a)7
- b)8
- c)9
- d)16
Correct answer is option 'B'. Can you explain this answer?
Number of generators of group Z16
a)
7
b)
8
c)
9
d)
16
|
|
Chirag Verma answered |
Since Z16 = {0, 1 , 2 ..... . 15}
The numbers 1, 3, 5, 7, 9, 11, 13,15 are the elements of Z16 that are relatively prime to 16. Each of these elements generates Z16.
So no. of generators = 8
So no. of generators = 8
Which of the following is a 2 -dimensional subspace of R3 over R ?- a)
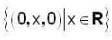
- b)
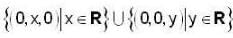
- c)
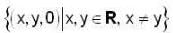
- d)
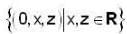
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a 2 -dimensional subspace of R3 over R ?
a)
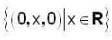
b)
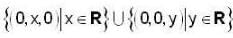
c)
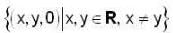
d)
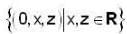
|
|
Chirag Verma answered |
Here (a) be a subspace but basis of it is {(0. 1, 0)} so it be a subspace of dimension 1.
(b), (c) are not subspace, so they don't have dim.
Now (d) be a subspace and its basis is {(0, 0. 1) (0, 1. 0)} so it be a subspace with dimension 2.
(b), (c) are not subspace, so they don't have dim.
Now (d) be a subspace and its basis is {(0, 0. 1) (0, 1. 0)} so it be a subspace with dimension 2.
How many numbers satisfied the equation x ≌ 7 (mod 17), where x in the range 1 < x < 100.- a)4
- b)5
- c)6
- d)7
Correct answer is option 'C'. Can you explain this answer?
How many numbers satisfied the equation x ≌ 7 (mod 17), where x in the range 1 < x < 100.
a)
4
b)
5
c)
6
d)
7
|
|
Devansh Choudhary answered |
The equation x ≡ 7 (mod 17) can be rewritten as x = 17k + 7, where k is an integer.
To find the range of x, we can substitute the given range 1 ≤ x ≤ 100 into the equation:
1 ≤ 17k + 7 ≤ 100
Subtracting 7 from all parts of the inequality:
-6 ≤ 17k ≤ 93
Dividing by 17:
-6/17 ≤ k ≤ 93/17
Since k must be an integer, we can round down the lower bound and round up the upper bound:
-1 ≤ k ≤ 5
Now we can find the number of values of x within this range:
For k = -1, we have x = 17(-1) + 7 = 0, which is not within the given range.
For k = 0, we have x = 17(0) + 7 = 7.
For k = 1, we have x = 17(1) + 7 = 24.
For k = 2, we have x = 17(2) + 7 = 41.
For k = 3, we have x = 17(3) + 7 = 58.
For k = 4, we have x = 17(4) + 7 = 75.
For k = 5, we have x = 17(5) + 7 = 92.
Therefore, there are 6 numbers (7, 24, 41, 58, 75, 92) that satisfy the equation x ≡ 7 (mod 17) within the given range 1 ≤ x ≤ 100.
To find the range of x, we can substitute the given range 1 ≤ x ≤ 100 into the equation:
1 ≤ 17k + 7 ≤ 100
Subtracting 7 from all parts of the inequality:
-6 ≤ 17k ≤ 93
Dividing by 17:
-6/17 ≤ k ≤ 93/17
Since k must be an integer, we can round down the lower bound and round up the upper bound:
-1 ≤ k ≤ 5
Now we can find the number of values of x within this range:
For k = -1, we have x = 17(-1) + 7 = 0, which is not within the given range.
For k = 0, we have x = 17(0) + 7 = 7.
For k = 1, we have x = 17(1) + 7 = 24.
For k = 2, we have x = 17(2) + 7 = 41.
For k = 3, we have x = 17(3) + 7 = 58.
For k = 4, we have x = 17(4) + 7 = 75.
For k = 5, we have x = 17(5) + 7 = 92.
Therefore, there are 6 numbers (7, 24, 41, 58, 75, 92) that satisfy the equation x ≡ 7 (mod 17) within the given range 1 ≤ x ≤ 100.
{0, 1, 2, 3, 4, 5} is a group under addition modulo 6, then the order of 1 is ___________.
Correct answer is '6'. Can you explain this answer?
{0, 1, 2, 3, 4, 5} is a group under addition modulo 6, then the order of 1 is ___________.
|
|
Chirag Verma answered |
(1)6 = 1 + 1 + 1 + 1 + 1 +1 = 6 (mod 6) = 0
∴ Older of 1 is 6.
∴ Older of 1 is 6.
Let T : V → w be a linear transformation, where V is a finite dimensional vector space. Let B be a subspace of W, then- a)T-1 (B) = φ
- b)T-1 (B) is a subspace of V
- c)dim ( ker T ) ≤ dim (T-1 (B))
- d)dim(T-1 (B)) ≤ dim (ker T)
Correct answer is option 'B,C'. Can you explain this answer?
Let T : V → w be a linear transformation, where V is a finite dimensional vector space. Let B be a subspace of W, then
a)
T-1 (B) = φ
b)
T-1 (B) is a subspace of V
c)
dim ( ker T ) ≤ dim (T-1 (B))
d)
dim(T-1 (B)) ≤ dim (ker T)
|
|
Siddharth Verma answered |
Be a linear operator on a finite-dimensional vector space V. Suppose that the only eigenvalues of T are scalars λ1, λ2, ..., λk. Prove that the characteristic polynomial of T is equal to (x - λ1)(x - λ2)...(x - λk).
Proof:
Let n be the dimension of V. Since T is a linear operator on V, we can represent T by a matrix A with respect to some basis of V. Let {v1, v2, ..., vn} be a basis of V. Then we can write Tvj as a linear combination of {v1, v2, ..., vn} for each j = 1, 2, ..., n.
Suppose that λ is an eigenvalue of T and let v be an eigenvector corresponding to λ. Then we have Tv = λv. Writing v as a linear combination of {v1, v2, ..., vn}, we have v = a1v1 + a2v2 + ... + anvn for some scalars a1, a2, ..., an.
Now, applying T to both sides of the equation, we have Tv = T(a1v1 + a2v2 + ... + anvn). By linearity of T, this becomes λv = a1Tv1 + a2Tv2 + ... + anTvn.
Since {v1, v2, ..., vn} is a basis, we can express each Tvi as a linear combination of {v1, v2, ..., vn}. Let Tvi = b1v1 + b2v2 + ... + bnvn for each i = 1, 2, ..., n.
Substituting these expressions into the equation above, we have λ(a1v1 + a2v2 + ... + anvn) = a1(b1v1 + b2v2 + ... + bnvn) + a2(b1v1 + b2v2 + ... + bnvn) + ... + an(b1v1 + b2v2 + ... + bnvn).
Expanding both sides and regrouping terms, we have (λ - b1)a1v1 + (λ - b2)a2v2 + ... + (λ - bn)anvn = 0.
Since {v1, v2, ..., vn} is linearly independent, the coefficients of each vi must be zero. This gives us a system of n linear equations in the variables a1, a2, ..., an. Since v is nonzero, at least one of the ai must be nonzero.
Since λ is an eigenvalue, the system of equations above has a nonzero solution. This means that the determinant of the coefficient matrix of the system is zero. Therefore, we have (λ - b1)(λ - b2)...(λ - bn) = 0.
Since λ can be any eigenvalue of T, we have the characteristic polynomial of T as (x - λ1)(x - λ2)...(x - λk), where λ1, λ2, ..., λk are the eigenvalues of T.
Proof:
Let n be the dimension of V. Since T is a linear operator on V, we can represent T by a matrix A with respect to some basis of V. Let {v1, v2, ..., vn} be a basis of V. Then we can write Tvj as a linear combination of {v1, v2, ..., vn} for each j = 1, 2, ..., n.
Suppose that λ is an eigenvalue of T and let v be an eigenvector corresponding to λ. Then we have Tv = λv. Writing v as a linear combination of {v1, v2, ..., vn}, we have v = a1v1 + a2v2 + ... + anvn for some scalars a1, a2, ..., an.
Now, applying T to both sides of the equation, we have Tv = T(a1v1 + a2v2 + ... + anvn). By linearity of T, this becomes λv = a1Tv1 + a2Tv2 + ... + anTvn.
Since {v1, v2, ..., vn} is a basis, we can express each Tvi as a linear combination of {v1, v2, ..., vn}. Let Tvi = b1v1 + b2v2 + ... + bnvn for each i = 1, 2, ..., n.
Substituting these expressions into the equation above, we have λ(a1v1 + a2v2 + ... + anvn) = a1(b1v1 + b2v2 + ... + bnvn) + a2(b1v1 + b2v2 + ... + bnvn) + ... + an(b1v1 + b2v2 + ... + bnvn).
Expanding both sides and regrouping terms, we have (λ - b1)a1v1 + (λ - b2)a2v2 + ... + (λ - bn)anvn = 0.
Since {v1, v2, ..., vn} is linearly independent, the coefficients of each vi must be zero. This gives us a system of n linear equations in the variables a1, a2, ..., an. Since v is nonzero, at least one of the ai must be nonzero.
Since λ is an eigenvalue, the system of equations above has a nonzero solution. This means that the determinant of the coefficient matrix of the system is zero. Therefore, we have (λ - b1)(λ - b2)...(λ - bn) = 0.
Since λ can be any eigenvalue of T, we have the characteristic polynomial of T as (x - λ1)(x - λ2)...(x - λk), where λ1, λ2, ..., λk are the eigenvalues of T.
Let ( y - C)2 = Cx be the primitive of  The no. of integral curves which will pass through (1, 2) is,
The no. of integral curves which will pass through (1, 2) is,- a)1
- b)2
- c)3
- d)0
Correct answer is option 'D'. Can you explain this answer?
Let ( y - C)2 = Cx be the primitive of  The no. of integral curves which will pass through (1, 2) is,
The no. of integral curves which will pass through (1, 2) is,
 The no. of integral curves which will pass through (1, 2) is,
The no. of integral curves which will pass through (1, 2) is,a)
1
b)
2
c)
3
d)
0

|
Sravya Mehta answered |
We have y(1) = 2
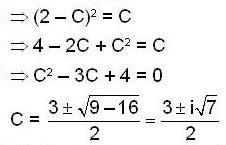
We have no real value of C.
We have no curve which passing through (1, 2).
We have no curve which passing through (1, 2).
If y1 and y2 are two solution of the differential equation 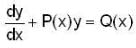 . Then which of the followings can be given as general soln of this differential eqn.
. Then which of the followings can be given as general soln of this differential eqn.- a)y(x) = c1 y1
- b)y(x) = c2 y2
- c)y(x) = y1 + C(y1 - y2)
- d)None of these
Correct answer is option 'A,B,C'. Can you explain this answer?
If y1 and y2 are two solution of the differential equation 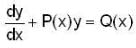 . Then which of the followings can be given as general soln of this differential eqn.
. Then which of the followings can be given as general soln of this differential eqn.
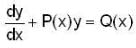 . Then which of the followings can be given as general soln of this differential eqn.
. Then which of the followings can be given as general soln of this differential eqn.a)
y(x) = c1 y1
b)
y(x) = c2 y2
c)
y(x) = y1 + C(y1 - y2)
d)
None of these
|
|
Chirag Verma answered |
Option (a), (b) are clearly correct
Now we have
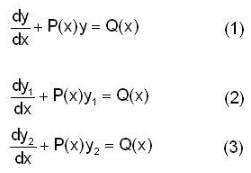
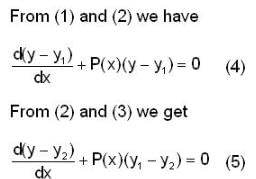
Now from (4) and (5)
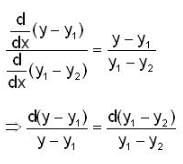
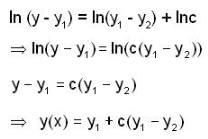
If G be an one empty set(1) a(bc) = (ab)c for all a, b, c ∈ G(2) For any a, b ∈ G, the equations ax = b and ya = b have solutions in G.
then- a)<G, •> is not group
- b)<G. •> is a group
- c)<G,•> is a sub group
- d)<G, •> is not a sub group.
Correct answer is option 'B'. Can you explain this answer?
If G be an one empty set
(1) a(bc) = (ab)c for all a, b, c ∈ G
(2) For any a, b ∈ G, the equations ax = b and ya = b have solutions in G.
then
then
a)
<G, •> is not group
b)
<G. •> is a group
c)
<G,•> is a sub group
d)
<G, •> is not a sub group.

|
Veda Institute answered |
Let (1) and (2) hold. To show G is a group, we need prove existence of identity and
Let a ∈ G be any element inverse.
By (2) the equations ax = a
ya = a
have solutions in G.
Let x = e and y = f be the solutions.
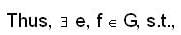
ae = a
fa = a
Let now b e G be any element then again by (2) 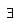 some x, y in G s.t.,
some x, y in G s.t.,
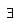 some x, y in G s.t.,
some x, y in G s.t.,ax = b
ya = b.
Now ax = b ⇒ f.(a.x) = f.b
⇒ (f.a).x = f.b
⇒ a.x = f.b
⇒ b = f.b
Again y.a = h
⇒ (y.a).e = b.e
⇒y.(a.e) = b.e
⇒ y.a = be
⇒ b = be
thus we have b = fb ... (i)
b = be ... (ii)
for any b ∈ G
Putting b = e in (i) and b = f in (ii) we get
e = fe
f = fe
⇒ e = f.
Hence ae = a = fa = ea
Hence ae = a = fa = ea
i.e., 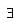 e ∈ G, s.t., ae = ea = a
e ∈ G, s.t., ae = ea = a
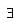 e ∈ G, s.t., ae = ea = a
e ∈ G, s.t., ae = ea = a⇒ e is identity.
Again, for any a ∈ G, and (the identity) e ∈ G, the equations ax = e and ya = e have solutions.
Let the solutions be x = a1, and y = a2
Again, for any a ∈ G, and (the identity) e ∈ G, the equations ax = e and ya = e have solutions.
Let the solutions be x = a1, and y = a2
then aa1 = e,
a2a = e
Now a1 = ea1 = (a2a)a1 = a2(aa1) = a2e = a2.
Hence aa1 = e = a1a for any a ∈ G
i.e., for any a ∈ G, 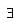 some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.
some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.
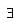 some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.
some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.Total number of non abelian groups of order 23 . 34. 5 is __________.
Correct answer is '15'. Can you explain this answer?
Total number of non abelian groups of order 23 . 34. 5 is __________.

|
Veda Institute answered |
Partitions of 3 are three namely
3 = 3,2 + 1, 1 +1 +1.
Partition of 4 are five namely
4 = 4, 3 + 1, 2 + 2, 2 + 1 +1, 1 +1 +1 +1.
Partition of 1 is only one 1 = 1
Thus there are (I) non isomorphic abelian group of order 2.
(II) five non isomorphic abelian group of order 34. and
(III) One abelian group of order 5.
Hence total number of non abelian group of order
23. 34. 5 = 3 x 5 x 1 = 1
=15
The area between the curves y = xex and y = xe-x and the line x = 1 is __________ ( Write upto Four decimal Places)
Correct answer is '0.7357'. Can you explain this answer?
The area between the curves y = xex and y = xe-x and the line x = 1 is __________ ( Write upto Four decimal Places)
|
|
Chirag Verma answered |
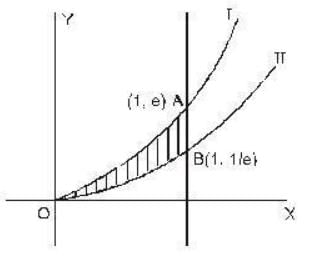
The line x = 1 meets the curves in (1,e) and B(1, 1/e). The second curve is lower cuive as ordinate of B is less than ordinate of A.
Both the curves pass through origin.
Both the curves pass through origin.
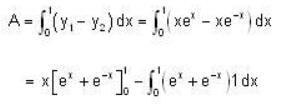
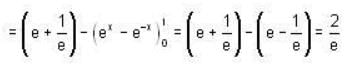
= 0.7357
For the three equations
-2x + y + z = a
x - 2y + z = b
x + y - 2z = c- a)have no solution unless a + b + c = 0
- b)when a + b + c = 0, then solution exist.
- c)have solution when a + b + c ≠ 0
- d)when a + b + c ≠ 0, then solution exist
Correct answer is option 'A,B'. Can you explain this answer?
For the three equations
-2x + y + z = a
x - 2y + z = b
x + y - 2z = c
-2x + y + z = a
x - 2y + z = b
x + y - 2z = c
a)
have no solution unless a + b + c = 0
b)
when a + b + c = 0, then solution exist.
c)
have solution when a + b + c ≠ 0
d)
when a + b + c ≠ 0, then solution exist
|
|
Chirag Verma answered |

Take augmented matrix

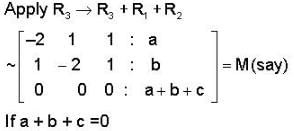
then Rank A = Rank M = 2,then system has solution otherwise no solution.
So if a + b + c = 0 then solution is exist.
So option A and B are correct.
Consider the differential equation y” + 9y = 0 with the boundary conditions, y(0) = 0, y(2π) = 1, then the differential equation has- a)A unique solution
- b)A singly infinite family of solutions
- c)No solution
- d)At least two solutions
Correct answer is option 'C'. Can you explain this answer?
Consider the differential equation y” + 9y = 0 with the boundary conditions, y(0) = 0, y(2π) = 1, then the differential equation has
a)
A unique solution
b)
A singly infinite family of solutions
c)
No solution
d)
At least two solutions

|
Veda Institute answered |
We have (D2 + 9)y = 0
⇒ y(x) = c1cos 3x + c2sin3x
y(0) = 0 ⇒c1 = 0
y(2π) = 1 ⇒ c1 = 1
⇒ DE has no solution.
If 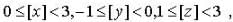 where [.] denotes the greatest integer function, then the minimum value of the determinant
where [.] denotes the greatest integer function, then the minimum value of the determinant 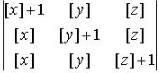 is _____.
is _____.
Correct answer is '1'. Can you explain this answer?
If 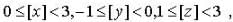 where [.] denotes the greatest integer function, then the minimum value of the determinant
where [.] denotes the greatest integer function, then the minimum value of the determinant 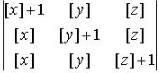 is _____.
is _____.
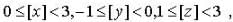 where [.] denotes the greatest integer function, then the minimum value of the determinant
where [.] denotes the greatest integer function, then the minimum value of the determinant 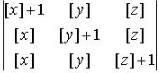 is _____.
is _____.|
|
Chirag Verma answered |
Here
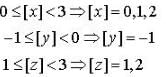
Thus the minimum value of the determinant will be given by
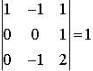
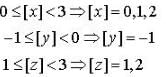
Thus the minimum value of the determinant will be given by
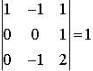
Let 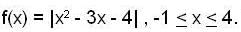 then, which of the follwing is not true ?
then, which of the follwing is not true ?- a)f(x) is monotonically increases in

- b)f(x) is monotonically decreases in
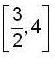
- c)f(x) is monotonically value of f(x) is 25/3
- d)The minimum value of f(x) is 0
Correct answer is option 'C'. Can you explain this answer?
Let 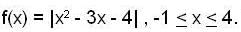 then, which of the follwing is not true ?
then, which of the follwing is not true ?
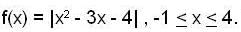 then, which of the follwing is not true ?
then, which of the follwing is not true ?a)
f(x) is monotonically increases in 

b)
f(x) is monotonically decreases in 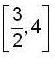
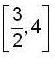
c)
f(x) is monotonically value of f(x) is 25/3
d)
The minimum value of f(x) is 0

|
Veda Institute answered |
we have
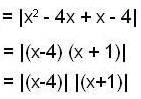
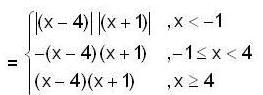
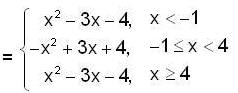
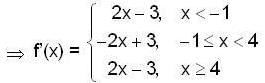
clearly when
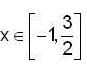
and f'(x) < 0
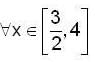
f is decreasing in 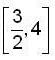
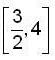
Now at x = -1, sign of f changes from -ive to +ive
=> at x = -1, f has minimum.
=> min f = 0 at x = 4 also f has minimum.
=> only option (c) is not true.
Which one of the following statements is true?- a)Every permutation is a cycle
- b)Every cycle is a permutation
- c)Sn is not cyclic for all n
- d)Every permutations s ∈ Sn can be written as product of (n - 1) transposition
Correct answer is option 'B,C,D'. Can you explain this answer?
Which one of the following statements is true?
a)
Every permutation is a cycle
b)
Every cycle is a permutation
c)
Sn is not cyclic for all n
d)
Every permutations s ∈ Sn can be written as product of (n - 1) transposition
|
|
Chirag Verma answered |
We know that every cycle is permutation but every permutation is not a cycle and it is also true that Sn is not cyclic for all n and every permutation s ∈ Sn can be written as product of (n -1) transposition.
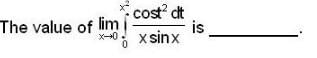
Correct answer is '1'. Can you explain this answer?
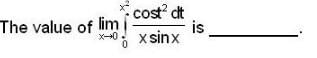

|
Veda Institute answered |
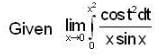
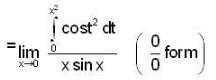
apply L-Hospital Rule, we get
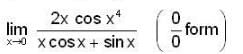
again apply L-Hospital Rule, we get
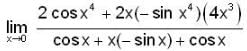
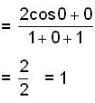
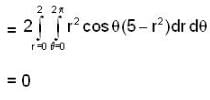
Let {an} be a sequence of non-negative real n o s such that the series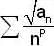 ,is convergent. If P is a real number such that the series
,is convergent. If P is a real number such that the series 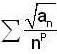 diverges, then
diverges, then- a)P must be strictly less than 1/2
- b)P must be strictly less than or equal to 1/2
- c)P must be strictly less than or equal to 1 but can be greater than 1/2
- d)P must be strictly less than 1 but can be greater than or equal to 1/2
Correct answer is option 'A'. Can you explain this answer?
Let {an} be a sequence of non-negative real n o s such that the series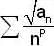 ,is convergent. If P is a real number such that the series
,is convergent. If P is a real number such that the series 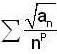 diverges, then
diverges, then
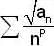 ,is convergent. If P is a real number such that the series
,is convergent. If P is a real number such that the series 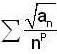 diverges, then
diverges, thena)
P must be strictly less than 1/2
b)
P must be strictly less than or equal to 1/2
c)
P must be strictly less than or equal to 1 but can be greater than 1/2
d)
P must be strictly less than 1 but can be greater than or equal to 1/2
|
|
Chirag Verma answered |

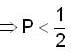
Chapter doubts & questions for Practice Test for IIT Jam Mathematics - IIT JAM Mathematics Mock Test Series 2025 is part of Mathematics exam preparation. The chapters have been prepared according to the Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Practice Test for IIT Jam Mathematics - IIT JAM Mathematics Mock Test Series in English & Hindi are available as part of Mathematics exam.
Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free.
IIT JAM Mathematics Mock Test Series
1 docs|26 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily
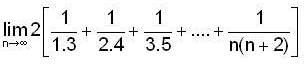 is equal to _______________
is equal to _______________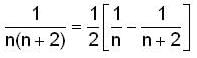
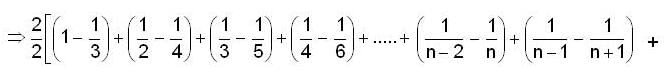
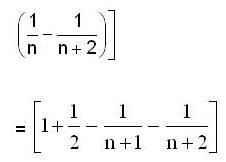
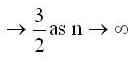

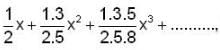 is ______.
is ______.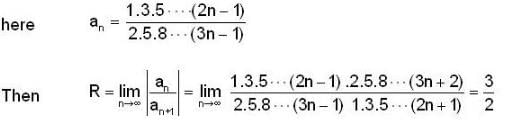

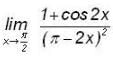 is equal to ..........
is equal to ..........
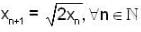 , then which of the following(s) is/are true for {xn}?
, then which of the following(s) is/are true for {xn}?

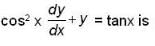
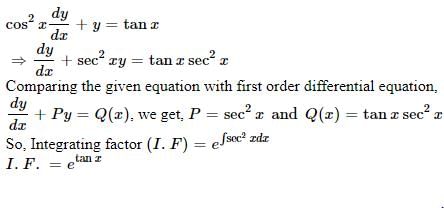
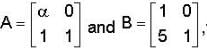 then value of a for which A2= B, is _____
then value of a for which A2= B, is _____
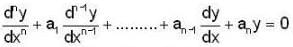 with real constant coefficients, then the least possible value of n is _________.
with real constant coefficients, then the least possible value of n is _________.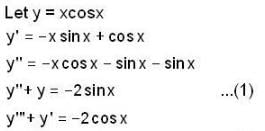
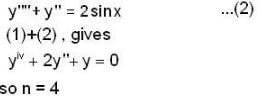
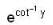
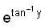


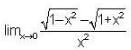 is given by ______
is given by ______
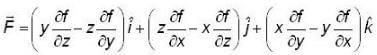 and
and 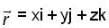 with r =
with r = 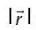 then which of the followings is /are true ? (where f be a SPF).
then which of the followings is /are true ? (where f be a SPF).
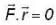
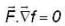

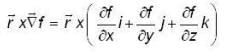
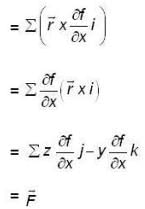

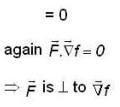
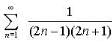 then its sum is equals to _____.
then its sum is equals to _____.
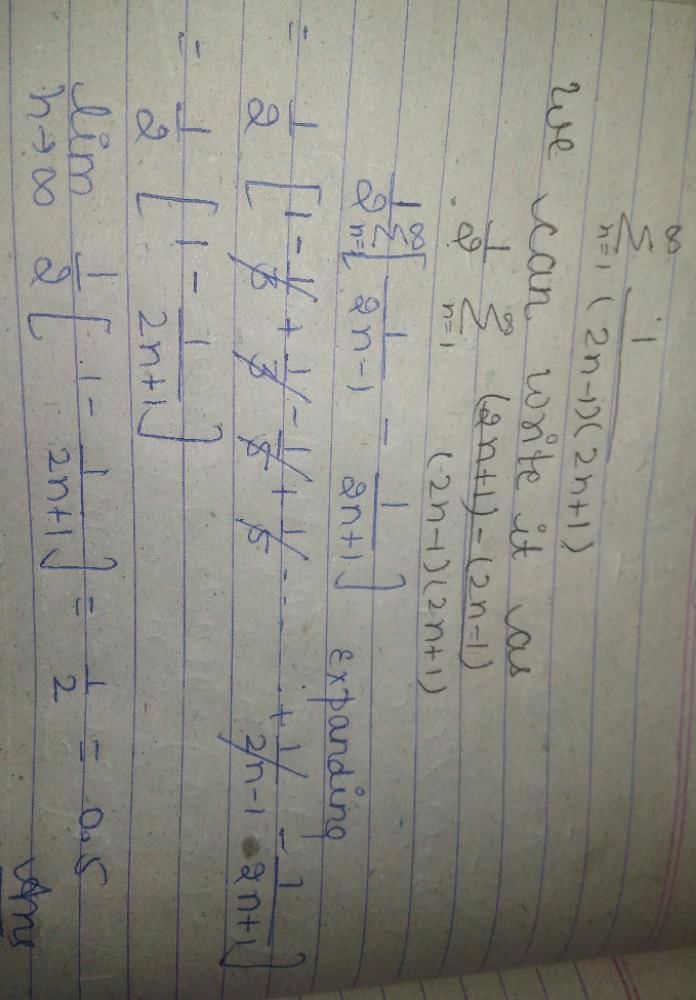
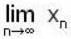 is equal to _________ .
is equal to _________ .
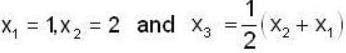
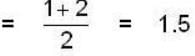
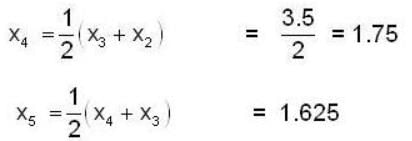
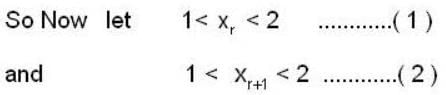
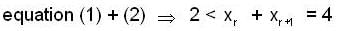
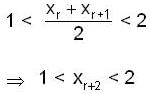

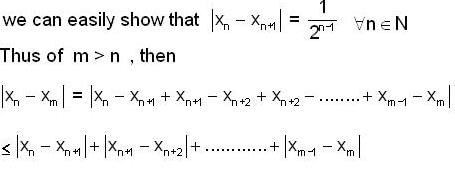
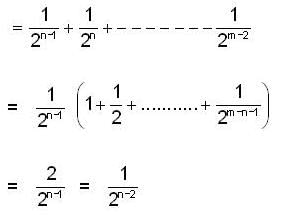
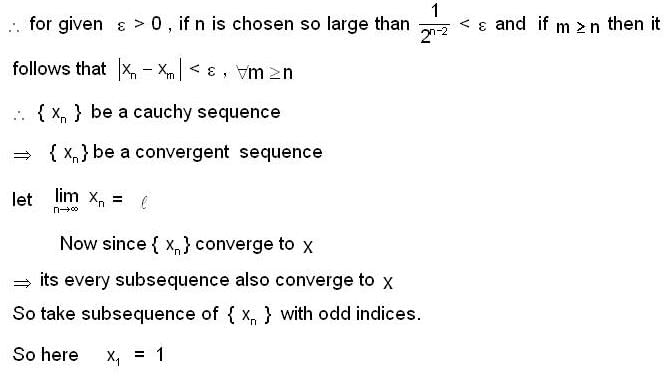
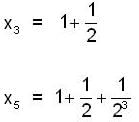
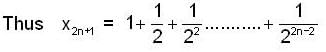
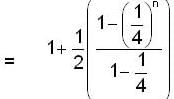

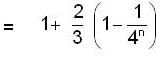
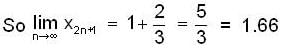
 is equal to _________, where
is equal to _________, where 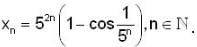

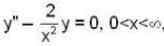 then which of the following(s) is/are not its 2nd L.l. solution.
then which of the following(s) is/are not its 2nd L.l. solution.