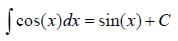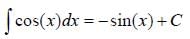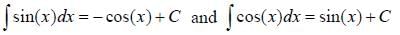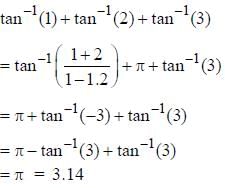All Exams >
Biotechnology Engineering (BT) >
Mock Test Series of IIT JAM Biotechnology 2026 >
All Questions
All questions of Maths for Biotechnology Engineering (BT) Exam
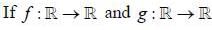 are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 are
are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 are- a)1, 2
- b)-1, 2
- c)-1, -2
- d)1, -2
Correct answer is option 'C'. Can you explain this answer?
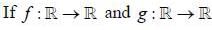 are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 are
are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 area)
1, 2
b)
-1, 2
c)
-1, -2
d)
1, -2

|
Anisha Banerjee answered |
Given that f(x) = 2x + 3, g(x) = x2+7
∴ g(f(x)) = g(2x + 3) = (2x + 3)2 + 7
= 4x2 + 9 + 12x+ 7 = 4x2 + 12x + 16
Given that g (f (x)) = 8
⇒ 4x2 + 12x + 16 = 8
⇒ 4x2 + 12x + 8 = 0
⇒ 4(x2 + 3x + 2) = 0
⇒ 4(x + l)(x + 2) = 0
∴ x = -1 and x = -2
∴ g(f(x)) = g(2x + 3) = (2x + 3)2 + 7
= 4x2 + 9 + 12x+ 7 = 4x2 + 12x + 16
Given that g (f (x)) = 8
⇒ 4x2 + 12x + 16 = 8
⇒ 4x2 + 12x + 8 = 0
⇒ 4(x2 + 3x + 2) = 0
⇒ 4(x + l)(x + 2) = 0
∴ x = -1 and x = -2
The function f(x) = |x|+|x - 1| is- a)Continuous at , but not differentiable at
- b)Both continuous and differentiable at x = 1
- c)Not continuous x = 1
- d)Not differentiable at x = 1
Correct answer is option 'A,D'. Can you explain this answer?
The function f(x) = |x|+|x - 1| is
a)
Continuous at , but not differentiable at
b)
Both continuous and differentiable at x = 1
c)
Not continuous x = 1
d)
Not differentiable at x = 1

|
Isha Bose answered |
Given that f (x) = |x| + |x-1|, then f(1) = 1
Since absolute volue functions are continuous everywhere so f(x) = |x| + |x-1|. being the sum of two continuous function is continuous everywhere. Now we check differentiability at x = 1, we have
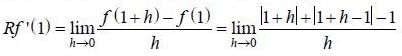
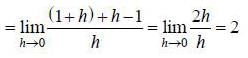
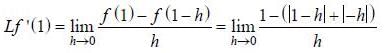

Hence Lf'(1) ≠ Rf'(1)
∴ Derivative do not exist at x = 1.
Since absolute volue functions are continuous everywhere so f(x) = |x| + |x-1|. being the sum of two continuous function is continuous everywhere. Now we check differentiability at x = 1, we have
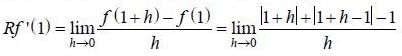
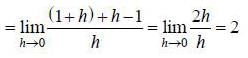
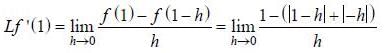

Hence Lf'(1) ≠ Rf'(1)
∴ Derivative do not exist at x = 1.
If Z is a complex number, then the minimum value of |z| + |z-l| is- a)1
- b)0
- c)1/2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If Z is a complex number, then the minimum value of |z| + |z-l| is
a)
1
b)
0
c)
1/2
d)
None of these

|
Pie Academy answered |
Note that
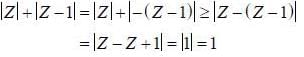
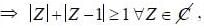
, hence minimum value is 1 and it is attained at Z = 0, 1/2
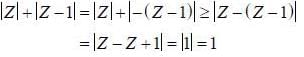
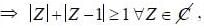
, hence minimum value is 1 and it is attained at Z = 0, 1/2
The value of log4(512) is- a)4.5
- b)9
- c)5
- d)128
Correct answer is option 'A'. Can you explain this answer?
The value of log4(512) is
a)
4.5
b)
9
c)
5
d)
128

|
Priya Saha answered |
log4(512) = log4(29) = log4(49/2) =9/2
=4.5
=4.5
The diffemetial equation representing the family of curves. y2 = 2c (x + √c). where c is positive parameter is of- a)order 1
- b)order 2
- c)degree 3
- d)degree 4
Correct answer is option 'A,C'. Can you explain this answer?
The diffemetial equation representing the family of curves. y2 = 2c (x + √c). where c is positive parameter is of
a)
order 1
b)
order 2
c)
degree 3
d)
degree 4
|
|
Pooja Choudhury answered |
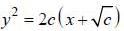 ......(1)
......(1)differentiating both side, we have
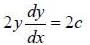
i.e.c =yy’ ...(2)
from (1) we have
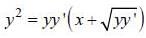

Squaring both side we have

Hence order of differential equation is 1 and degree is 3.
The area bounded by the curves y = |x| -1 and y = - |x| +1 is- a)1
- b)2
- c)2√2
- d)4
Correct answer is option 'B'. Can you explain this answer?
The area bounded by the curves y = |x| -1 and y = - |x| +1 is
a)
1
b)
2
c)
2√2
d)
4

|
Vandana Gupta answered |
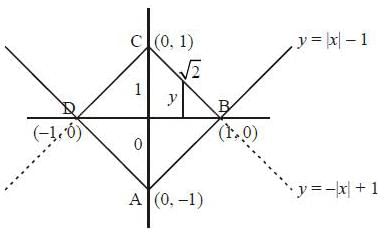
Method-I: From the figure, it is clear that ABCD fonn a square having each side √2.
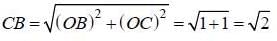
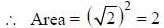
Method -II: Area ofABCD = 4 x Area of OBC
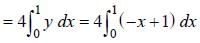 (as equation of CB is y = -x+ 1)
(as equation of CB is y = -x+ 1)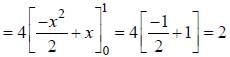
The product of all real roots of the equation x2 - |x| - 6 = 0 is- a)-9
- b)6
- c)9
- d)36
Correct answer is option 'A'. Can you explain this answer?
The product of all real roots of the equation x2 - |x| - 6 = 0 is
a)
-9
b)
6
c)
9
d)
36

|
Raghav Rane answered |
Equation is x2 - |x| - 6 = 0
Case I: x > 0. then we have
x2 - x - 6 = 0 (lx| = x)
⇒ (x-3)(x+2) = 0
⇒ x = 3 is the solution as x > 0.
(So x = -2 can’t be solution)
Case II: x < 0. then we have
x2 + x - 6 = 0 (|x| = -x)
⇒ (x + 3)(x - 2) = 0
⇒ x = -3 is the solution as x < 0
(So x = 2 can't be solution)
∴ product of roots = 3. - 3 = -9
Case I: x > 0. then we have
x2 - x - 6 = 0 (lx| = x)
⇒ (x-3)(x+2) = 0
⇒ x = 3 is the solution as x > 0.
(So x = -2 can’t be solution)
Case II: x < 0. then we have
x2 + x - 6 = 0 (|x| = -x)
⇒ (x + 3)(x - 2) = 0
⇒ x = -3 is the solution as x < 0
(So x = 2 can't be solution)
∴ product of roots = 3. - 3 = -9
The radius of the circle x2 + y2 - 2x + 4y = 8- a)
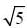
- b)
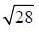
- c)
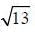
- d)
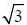
Correct answer is option 'C'. Can you explain this answer?
The radius of the circle x2 + y2 - 2x + 4y = 8
a)
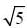
b)
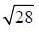
c)
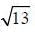
d)
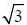
|
|
Vikram Kapoor answered |
Given circle x2 + y2 - 2x + 4y - 8 = 0
Comparing with the general equation of circle x2 + y2 + 2gx + 2fy - c = 0, we get g = -1. f = 2, c = -8
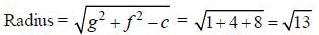
Comparing with the general equation of circle x2 + y2 + 2gx + 2fy - c = 0, we get g = -1. f = 2, c = -8
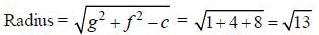
The distance between the lines 3x + 4y = 9 and 6x + 8y = 15 is _______.
Correct answer is '0.3'. Can you explain this answer?
The distance between the lines 3x + 4y = 9 and 6x + 8y = 15 is _______.

|
Soumya Sharma answered |
3x + 4y = 9 and 6x + 8y = 15
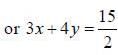
We know that the distance between the two parallel lines ax + by = c1 and ax + by = c2 is
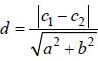
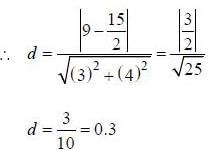
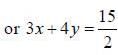
We know that the distance between the two parallel lines ax + by = c1 and ax + by = c2 is
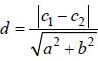
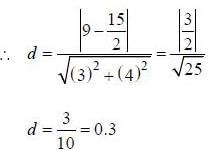
The number of arrangements of the letters of the word BANANA in which the two N’s do not appear adjacently is _____________.
Correct answer is '40'. Can you explain this answer?
The number of arrangements of the letters of the word BANANA in which the two N’s do not appear adjacently is _____________.

|
Bhavana Dasgupta answered |
In BANANA. Letter A reapets 3 times and N reapets 2 times.
Total number of arrangements of word BANANA is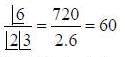
Let both N s are appear together, then they are considered is single letter.
In this way total number of arrangements are
Hence total number of arrangements where N do not appear adjacently is = 60 - 20 = 40
Total number of arrangements of word BANANA is
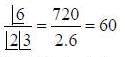
Let both N s are appear together, then they are considered is single letter.
In this way total number of arrangements are

Hence total number of arrangements where N do not appear adjacently is = 60 - 20 = 40
If α, β and γ are complex solution of equation a3 =1 then- a)α + β + γ =0
- b)αβγ=1
- c)α2 + β2 + γ2 =0
- d)αβ + βγ + γα = 0
Correct answer is option 'A,B,C,D'. Can you explain this answer?
If α, β and γ are complex solution of equation a3 =1 then
a)
α + β + γ =0
b)
αβγ=1
c)
α2 + β2 + γ2 =0
d)
αβ + βγ + γα = 0

|
Sanaya Kulkarni answered |
x3 = 1= >x3 - l = 0
=>(x-1)(x2 + x + 1) =0
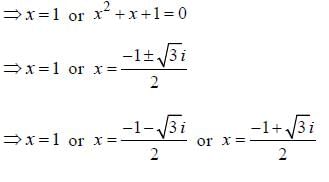
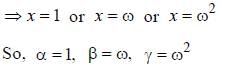

=>(x-1)(x2 + x + 1) =0
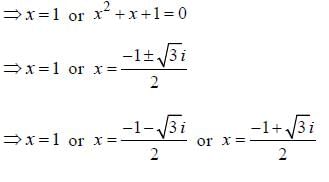
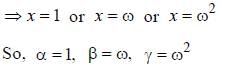

Two dice are rolled simultaneously. The probability that the sum of the two numbers on the top faces will be at least 10 is- a)1/6
- b)1/12
- c)1/18
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Two dice are rolled simultaneously. The probability that the sum of the two numbers on the top faces will be at least 10 is
a)
1/6
b)
1/12
c)
1/18
d)
none of these

|
Ameya Rane answered |
Two dice are rolled simultaneously, hence total number of elements in sample space is = 6 * 6 = 36
We have event E is the collection of those elements having sum greater or equal than 10.
i.e. E = {(4,6),(5.6).(6.6).(6.5).(6.4).(5.5)}
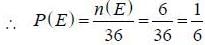
We have event E is the collection of those elements having sum greater or equal than 10.
i.e. E = {(4,6),(5.6).(6.6).(6.5).(6.4).(5.5)}
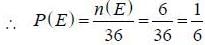
On the interval [0,1], the function f(x) = x25 (1 - x)75 takes its maximum value at the point _______.
Correct answer is '0.25'. Can you explain this answer?
On the interval [0,1], the function f(x) = x25 (1 - x)75 takes its maximum value at the point _______.

|
Tanishq Goyal answered |

For critical point, we have f'(x) = 0
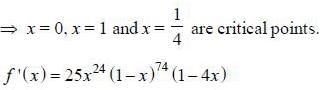
Note that sign of f' (x) depends on the sign of (1 - 4x).
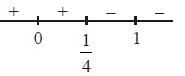
hence f (x) is increasing when
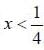 and f (x) is decreasing when
and f (x) is decreasing when 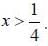
∴ f (x) is maximum at x = 1/4
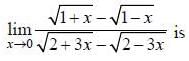
- a)Does not exist
- b)Lies between 0 and 1/2
- c)Lies between 1/2 and 1
- d)Greater than 1
Correct answer is option 'B'. Can you explain this answer?
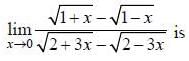
a)
Does not exist
b)
Lies between 0 and 1/2
c)
Lies between 1/2 and 1
d)
Greater than 1

|
Raksha Pillai answered |
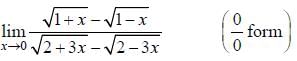
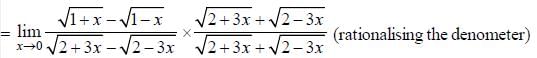
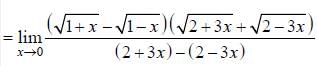
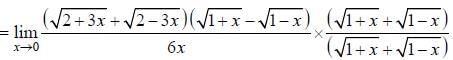
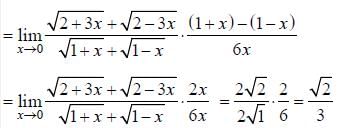
Hence limit lies between 0 and 1/2
The equations of lines which pass through the point (3, -2) and are inclined at 60° to the line 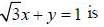
- a)y + 2 = 0
- b)x - 2 = 0
- c)

- d)
Correct answer is option 'A,C'. Can you explain this answer?
The equations of lines which pass through the point (3, -2) and are inclined at 60° to the line 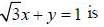
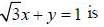
a)
y + 2 = 0
b)
x - 2 = 0
c)

d)
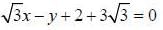

|
Preethi Joshi answered |
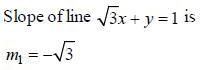
Let slope of a line making 60° angle with
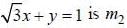
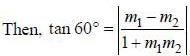
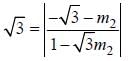
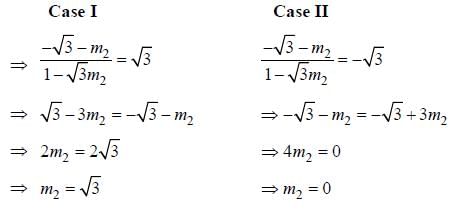
So. there will be two lines of such type. One is having slope
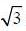 and the otehr one is having slope 0.
and the otehr one is having slope 0. Therefore.
Line 1: passing through (3, -2) and slope
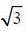

Line 2: passing through (3.-2) and slope 0.
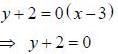
Option (A) and (C) are correct.
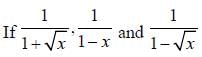 are consecutive forms of a series, then series is
are consecutive forms of a series, then series is- a)H.P
- b)G.P
- c)A.P
- d)Both A.P and G.P
Correct answer is option 'C'. Can you explain this answer?
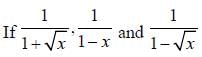 are consecutive forms of a series, then series is
are consecutive forms of a series, then series isa)
H.P
b)
G.P
c)
A.P
d)
Both A.P and G.P

|
Yash Roy answered |
Note that if a. b. c are three consecutive terms
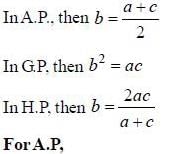
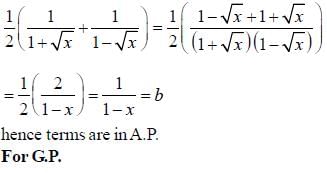
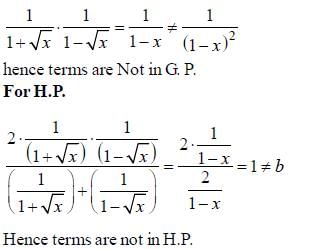
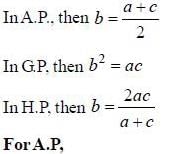
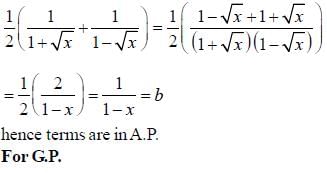
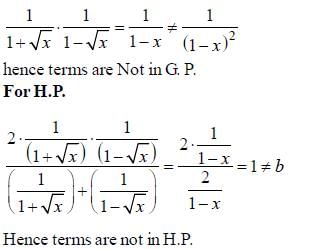
If 0 and 1 are roots of equation ax2 + bx + c = 0 where a ≠ 0 then a2 -b2 +c2 is equal to- a)-1
- b)0
- c)1
- d)Not possible
Correct answer is option 'B'. Can you explain this answer?
If 0 and 1 are roots of equation ax2 + bx + c = 0 where a ≠ 0 then a2 -b2 +c2 is equal to
a)
-1
b)
0
c)
1
d)
Not possible

|
Saranya Mehta answered |
ax2 + bx + c = 0
x = 0 is a solution =>0 + 0 + c = 0
=> c = 0
x = 1 is a solution =>a + b + c = 0
=> a + b = 0
= > b = - a
= > b2 = a2
so, a2 - b2 + c2 =02 + 02 = 0
x = 0 is a solution =>0 + 0 + c = 0
=> c = 0
x = 1 is a solution =>a + b + c = 0
=> a + b = 0
= > b = - a
= > b2 = a2
so, a2 - b2 + c2 =02 + 02 = 0
Let R = {(3,3),(6.6),(9,9),(12,12),(6.12),(3,9),(3,12),(3,6)} be a relation on the se A = {3,6,9,12}. The relation is- a)Reflexive and transitive
- b)Reflexive only
- c)Ail equivalence relation
- d)None
Correct answer is option 'D'. Can you explain this answer?
Let R = {(3,3),(6.6),(9,9),(12,12),(6.12),(3,9),(3,12),(3,6)} be a relation on the se A = {3,6,9,12}. The relation is
a)
Reflexive and transitive
b)
Reflexive only
c)
Ail equivalence relation
d)
None

|
Srishti Kulkarni answered |
(d) : For (3, 9) ∈ R, (9, 3) ∉ R
Therefore,relation is not symmetric which means our choice
(a) and (b) are out of court. We need to prove reflexivity and transitivity.
For reflexivity a ∈ R, (a, a) ∈ R which is hold i.e. R is reflexive. Again,
for transitivity of (a, b) ∈ R , (b, c) ∈ R
⇒ (a, c) ∈ R
which is also true in R = {(3, 3)(6, 6), (9, 9), (12, 12), (6,12), (3, 9), (3, 12), (3, 6)}.
If X and 7are two sets, then
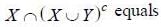
- a)X
- b)Y
- c)φ
- d)None
Correct answer is option 'C'. Can you explain this answer?
If X and 7are two sets, then
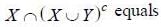
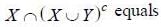
a)
X
b)
Y
c)
φ
d)
None

|
Shivam Khanna answered |
 (using De'morgans law)
(using De'morgans law) 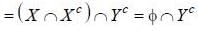
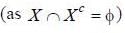
= φ
The value of f' (1) where f(x) = 1 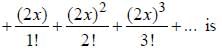
- a)2e
- b)2e2
- c)e2
- d)e
Correct answer is option 'B'. Can you explain this answer?
The value of f' (1) where f(x) = 1 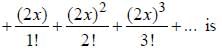
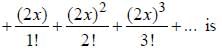
a)
2e
b)
2e2
c)
e2
d)
e

|
Nandini Das answered |

f(x) = e2x
f'(x) = 2.e2x
f'(1) = 2.e2
f'(x) = 2.e2x
f'(1) = 2.e2
If E = {1,2,3,4} and F = {1,2}, then the niunber of onto functions on E to F is ______.
Correct answer is '14'. Can you explain this answer?
If E = {1,2,3,4} and F = {1,2}, then the niunber of onto functions on E to F is ______.

|
Sinjini Nair answered |
n(E) = 4 n(F) = 2
Then total number of onto functions from E to F are =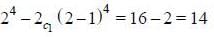
Note: If n(A) = n and n(B) = m then total number of onto functions from A to B are
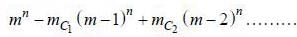
Then total number of onto functions from E to F are =
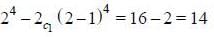
Note: If n(A) = n and n(B) = m then total number of onto functions from A to B are
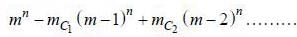
The distance from origin to the centre of a circle x2 + y2 - 4x - 6y + 4 = 0 is- a)2
- b)3
- c)
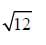
- d)

Correct answer is option 'D'. Can you explain this answer?
The distance from origin to the centre of a circle x2 + y2 - 4x - 6y + 4 = 0 is
a)
2
b)
3
c)
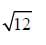
d)


|
Rutuja Sengupta answered |
x2 + y2 - 4x - 6y + 4 = 0
=>(x-2)2+ ( y - 3 )2 = 4 - 4 + 9
=> (x- 2)2 + (y- 3)2 = 32
Centre (2, 3) and origin (0,0)
Distance between origin and centre
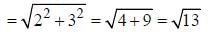
=>(x-2)2+ ( y - 3 )2 = 4 - 4 + 9
=> (x- 2)2 + (y- 3)2 = 32
Centre (2, 3) and origin (0,0)
Distance between origin and centre
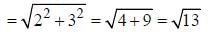
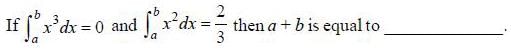
Correct answer is '0'. Can you explain this answer?
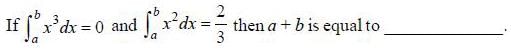

|
Abhishek Nambiar answered |

Clearly from options, we have
b = 1. a = -1
Hence (0) is answer
In throwing a die, let
A be the event 'coining up of an odd number'
B be the event 'coming up of an even number'
C' be the event ‘coming up of a number > 4' and D be the event ‘coming up of a number <3'
Then- a)A and B are mutally exclusive and exhautive
- b)A and C are mutually exclusive and exhautive
- c)A, C and D form an exhautive system
- d)B, C and D form an exhautive system
Correct answer is option 'A,C'. Can you explain this answer?
In throwing a die, let
A be the event 'coining up of an odd number'
B be the event 'coming up of an even number'
C' be the event ‘coming up of a number > 4' and D be the event ‘coming up of a number <3'
Then
A be the event 'coining up of an odd number'
B be the event 'coming up of an even number'
C' be the event ‘coming up of a number > 4' and D be the event ‘coming up of a number <3'
Then
a)
A and B are mutally exclusive and exhautive
b)
A and C are mutually exclusive and exhautive
c)
A, C and D form an exhautive system
d)
B, C and D form an exhautive system

|
Akash Kulkarni answered |
For throwing a dice, sample space S = {1,2,3,4,5,6} and
A = {1,3,5}
B = {2,4,6}
C = {4,5,6}
D = {1,2}
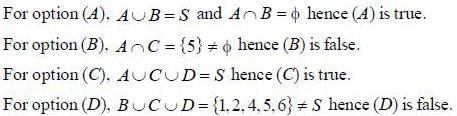
A = {1,3,5}
B = {2,4,6}
C = {4,5,6}
D = {1,2}
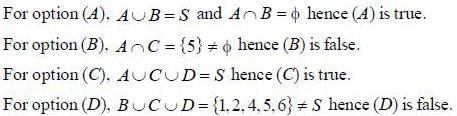
Chapter doubts & questions for Maths - Mock Test Series of IIT JAM Biotechnology 2026 2025 is part of Biotechnology Engineering (BT) exam preparation. The chapters have been prepared according to the Biotechnology Engineering (BT) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Biotechnology Engineering (BT) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Maths - Mock Test Series of IIT JAM Biotechnology 2026 in English & Hindi are available as part of Biotechnology Engineering (BT) exam.
Download more important topics, notes, lectures and mock test series for Biotechnology Engineering (BT) Exam by signing up for free.
Mock Test Series of IIT JAM Biotechnology 2026
7 docs|34 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily
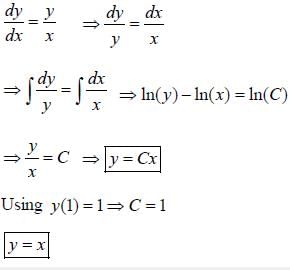

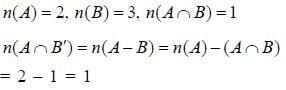
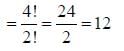
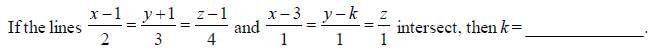
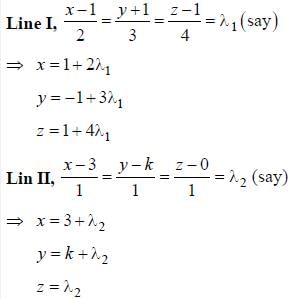
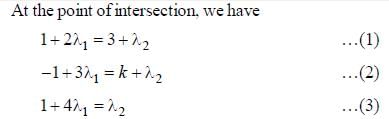
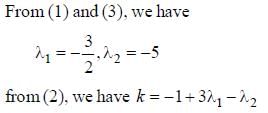
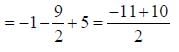
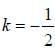
 is ____________________.
is ____________________.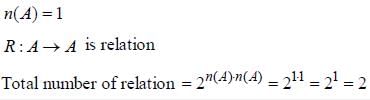
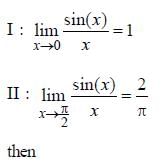
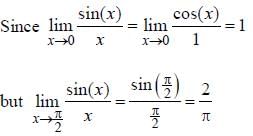
 then f (100) + f (-100) +
then f (100) + f (-100) + 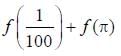 is equal to ____________.
is equal to ____________.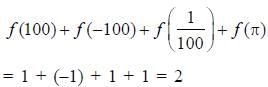
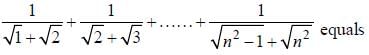
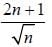
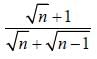

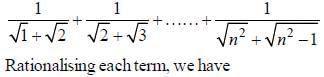
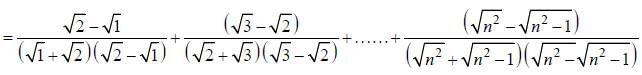
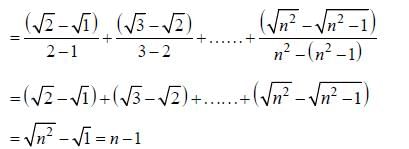
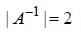
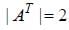
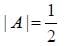

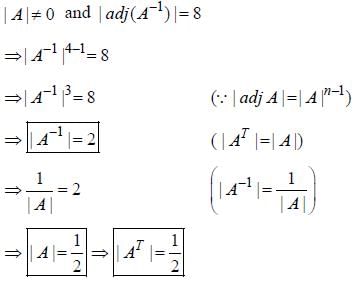
 is both continuous and differentiable function then a + b = _____________.
is both continuous and differentiable function then a + b = _____________.
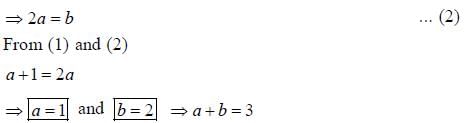

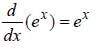
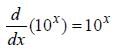

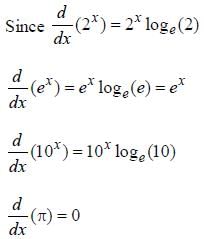
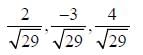
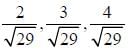
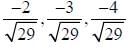

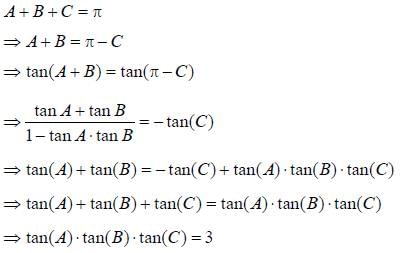
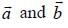 are unit vectors inclined with angle 60° then
are unit vectors inclined with angle 60° then 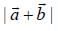 is equal to
is equal to