All questions of Theory of Computation for Computer Science Engineering (CSE) Exam
Over the alphabet , {0,1} consider the language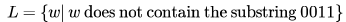
Which of the following is true about L.- a)L is not context free
- b)L is regular
- c)L is not regular but it is context free
- d)L is context free but not recursively enumerable
Correct answer is option 'B'. Can you explain this answer?
Over the alphabet , {0,1} consider the language
Which of the following is true about L.
a)
L is not context free
b)
L is regular
c)
L is not regular but it is context free
d)
L is context free but not recursively enumerable
|
Raj Sen answered |
L is regular.
Which one of the following languages over Σ = {a, b} is NOT context-free?- a){wwR |w ϵ {a, b}*}
- b){wanbnwR |w ∈ {a, b}*, n ≥ 0}
- c){wanwRbn|w ∈ {a, b}*, n ≥ 0}
- d){anbi |i ∈ {n, 3n, 5n}, n ≥ 0}
Correct answer is option 'C'. Can you explain this answer?
Which one of the following languages over Σ = {a, b} is NOT context-free?
a)
{wwR |w ϵ {a, b}*}
b)
{wanbnwR |w ∈ {a, b}*, n ≥ 0}
c)
{wanwRbn|w ∈ {a, b}*, n ≥ 0}
d)
{anbi |i ∈ {n, 3n, 5n}, n ≥ 0}
|
Sudhir Patel answered |
- {wanbnwR |w ∈ {a, b}*, n ≥ 0} is accepted by a non-deterministic pushdown automaton and hence it is a context-free language
- {wwR |w ϵ {a, b}*} is accepted by a non-deterministic pushdown automaton and hence it is context-free language.
- {wanwRbn|w ∈ {a, b}*, n ≥ 0} is not accepted by a pushdown automaton and hence it is not a context-free language.
- i = n, 2n, 3n, 4n, etc. forms and arithmetic series. anbn, anb2n and anb3n is accepted by a deterministic pushdown automaton and context-free language are closed under union and hence anbn ∪ anb2n ∪ anb3n is a context-free language. Hence {anbi |i ∈ {n, 3n, 5n}, n ≥ 0} is a context-free language.
Which of the following is not true?- a)Any LL grammar is unambiguous.
- b)DCFL’s are never inherently ambiguous.
- c)If G is an LR(k) grammar, then L(G) is a DCFL.
- d)All CFL’s which are not DCFL’s are ambiguous.
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not true?
a)
Any LL grammar is unambiguous.
b)
DCFL’s are never inherently ambiguous.
c)
If G is an LR(k) grammar, then L(G) is a DCFL.
d)
All CFL’s which are not DCFL’s are ambiguous.
|
Nishanth Roy answered |
• Every LL grammar must be unambiguous but every unambiguous need not be LL grammar.
• Ambiguity in language starts from CFL. So, DCFL cannot be inherently ambiguous.
• if G is an LR(K) grammar, then L{G) is a DCFL.
• Every CFL’s which are not DCFL need not be ambiguous.
• Ambiguity in language starts from CFL. So, DCFL cannot be inherently ambiguous.
• if G is an LR(K) grammar, then L{G) is a DCFL.
• Every CFL’s which are not DCFL need not be ambiguous.
Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol:
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?- a){(ab)n (cb)n | n ≥ 1}
- b){(ab)n cbm1 cbm2 .... cbmn |n, m1, m2 ....., mn ≥ 1}
- c){(ab)n (cbm)n | m, n ≥ 1}
- d){(ab)n (cbn)m | m, n ≥ 1}
Correct answer is option 'B'. Can you explain this answer?
Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol:
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?
a)
{(ab)n (cb)n | n ≥ 1}
b)
{(ab)n cbm1 cbm2 .... cbmn |n, m1, m2 ....., mn ≥ 1}
c)
{(ab)n (cbm)n | m, n ≥ 1}
d)
{(ab)n (cbn)m | m, n ≥ 1}
|
Riverdale Learning Institute answered |
S → abScT
→ ababScTcT (∵ S → abScT)
→ abababcTcTcT (∵ S → abcT)
→ abababcbTcTcT (∵ T → bT)
→ abababcbbTcTcT (∵ T → bT)
→ abababcbbbTcTcT (∵ T → bT)
→ abababcbbbbcTcT (∵ T → b)
→ abababcbbbbcbcT (∵ T → b)
→ abababcbbbbcbcbT (∵ T → bT)
→ abababcbbbbcbcbb (∵ T → b)
abababcbbbbcbcbb = (ab)3cb4cbcb2
From this string, it is clear that all the option 1),3) and 4) are not generated by given grammar.
→ ababScTcT (∵ S → abScT)
→ abababcTcTcT (∵ S → abcT)
→ abababcbTcTcT (∵ T → bT)
→ abababcbbTcTcT (∵ T → bT)
→ abababcbbbTcTcT (∵ T → bT)
→ abababcbbbbcTcT (∵ T → b)
→ abababcbbbbcbcT (∵ T → b)
→ abababcbbbbcbcbT (∵ T → bT)
→ abababcbbbbcbcbb (∵ T → b)
abababcbbbbcbcbb = (ab)3cb4cbcb2
From this string, it is clear that all the option 1),3) and 4) are not generated by given grammar.
Which of the following is false?
- a)The languages accepted by FA’s are regular languages.
- b)Every DFA is an NFA.
- c)There are some NFA’s for which no DFA can be constructed.
- d)If L is accepted by an NFA with ∈ transition then L is accepted by an NFA without ∈ transition.
Correct answer is option 'C'. Can you explain this answer?
Which of the following is false?
a)
The languages accepted by FA’s are regular languages.
b)
Every DFA is an NFA.
c)
There are some NFA’s for which no DFA can be constructed.
d)
If L is accepted by an NFA with ∈ transition then L is accepted by an NFA without ∈ transition.
|
Ravi Singh answered |
There are some NFA's for which no DFA can be constructed.
Explanation:
Explanation:
Option 3 is false because every NFA (Nondeterministic Finite Automaton) can be converted into an equivalent DFA (Deterministic Finite Automaton). This conversion is known as the subset construction or powerset construction.
The subset construction algorithm allows us to construct a DFA that recognizes the same language as a given NFA. Therefore, for any NFA, it is always possible to construct a DFA that accepts the same language.
Hence, the correct answer is 3. There are no NFAs for which no DFA can be constructed.
The language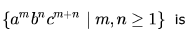 
- a)regular
- b)context-free but not regular
- c)context-sensitive but not context free
- d)type-0 but not context sensitive
Correct answer is option 'B'. Can you explain this answer?
The language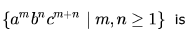
a)
regular
b)
context-free but not regular
c)
context-sensitive but not context free
d)
type-0 but not context sensitive
|
|
Pallavi Reddy answered |
Language is not regular bcoz we need to match count of c's is equal to count of b's + count of a's
and that can implement by PDA
∂(q0,a,^)= (q0,a) [ push a in stack, as per language a comes first]
∂(q0,a,a)= (q0,aa) [push all a's into stack]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q2,c,b) = (q2,c) [ pop one b's for each c and continue same ]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
Note :1. state changes make sure b's comes after a and c's comes after b's]
How many minimum number of states are required in the DFA (over the alphabet {a, b}) accepting all the strings with the number of a’s divisible by 4 and number of b’s divisible by 5?- a)20
- b)9
- c)7
- d)15
Correct answer is option 'A'. Can you explain this answer?
How many minimum number of states are required in the DFA (over the alphabet {a, b}) accepting all the strings with the number of a’s divisible by 4 and number of b’s divisible by 5?
a)
20
b)
9
c)
7
d)
15
|
Naina Shah answered |
For DFA accepting all the strings with number of a’s divisible by 4; four states are required similarly for DFA accepting all the strings with number of b’s divisible by 5, five states are required and for their combination, states will be multiplied. So 5 x 4 = 20 states will be required.
Which of the following are regular languages?
(i) The language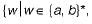 
w has an odd number of b’s}.
(ii) The language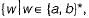 
w has an even number of b’s).
(iii) The language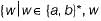 
has an even number of b’s and odd number of a’s).- a)(i) and (ii) only
- b)(i) only
- c)(ii) only
- d)All of these
Correct answer is option 'D'. Can you explain this answer?
Which of the following are regular languages?
(i) The language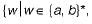 w has an odd number of b’s}.
(ii) The language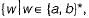 w has an even number of b’s).
(iii) The language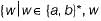 has an even number of b’s and odd number of a’s).
(i) The language
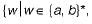w has an odd number of b’s}.(ii) The language
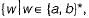w has an even number of b’s).(iii) The language
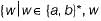has an even number of b’s and odd number of a’s).a)
(i) and (ii) only
b)
(i) only
c)
(ii) only
d)
All of these
|
|
Ravi Singh answered |
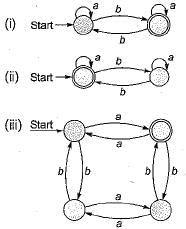
As we can construct the DFA for the given languages, hence all of the given languages are regular.
Let denote the languages generated by the grammar S→ 0S0 I 00.Which of the following is TRUE?- a)L=0+
- b)L is regular but not 0+
- c) L is context free but not regular
- d)L is not context free
Correct answer is option 'B'. Can you explain this answer?
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
a)
L=0+
b)
L is regular but not 0+
c)
L is context free but not regular
d)
L is not context free
|
Aditya Deshmukh answered |
Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0’s ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,…}, i.e only even no of 0’s ( excluding empty string}.
Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)
Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+.
Option B : Hence This option is Correct, because L is Regular but not 0+, as we proved above.
Consider the following statements about L:
(i) L is accepted by multi-tape turing machine M1.
(ii) L is also accpted by a single tape turing machine M2.
Which of the following statement is correct?- a)Acceptance by M2 is slower by O(n2)
- b)Acceptance of M2 is slower by O(n)
- c)Acceptance of M2 is faster by O(n2)
- d)Acceptabce by M2 is faster by 0(n)
Correct answer is option 'A'. Can you explain this answer?
Consider the following statements about L:
(i) L is accepted by multi-tape turing machine M1.
(ii) L is also accpted by a single tape turing machine M2.
Which of the following statement is correct?
(i) L is accepted by multi-tape turing machine M1.
(ii) L is also accpted by a single tape turing machine M2.
Which of the following statement is correct?
a)
Acceptance by M2 is slower by O(n2)
b)
Acceptance of M2 is slower by O(n)
c)
Acceptance of M2 is faster by O(n2)
d)
Acceptabce by M2 is faster by 0(n)
|
Ashwin Dasgupta answered |
While simulating multi-tape TM on a single tape TM, the head has to move at least 2k cells per move, where k is the number of tracks on single tape TM. Thus for k moves, we get
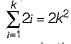
which means quadratic slow down. Thus, acceptance by single-tape is slower by 0(n2).
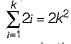
which means quadratic slow down. Thus, acceptance by single-tape is slower by 0(n2).
Which of the following functions are computable with Turning Machine?- a)n*( n - 1)*(n- 2)* . . , * 2* 1*
- b)[log2n]
- c)22n
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following functions are computable with Turning Machine?
a)
n*( n - 1)*(n- 2)* . . , * 2* 1*
b)
[log2n]
c)
22n
d)
All of the above
|
Akshay Singh answered |
All the above functions are total recursive functions. The total recursive functions are like recursive language. Turing machine halts on each and every input of recursive language. All of the above functions are turing computable.
If the strings of a language L can be effectively enumerated in lexicographic (i.e. alphabetic) order which of the following statements is true?- a)L is necessarily finite
- b)L is regular but not necessarily finite
- c)L is context free but not necessarily regular
- d)L is recursive but not necessarily context free
Correct answer is option 'D'. Can you explain this answer?
If the strings of a language L can be effectively enumerated in lexicographic (i.e. alphabetic) order which of the following statements is true?
a)
L is necessarily finite
b)
L is regular but not necessarily finite
c)
L is context free but not necessarily regular
d)
L is recursive but not necessarily context free
|
|
Priyanka Ahuja answered |
L is recursive iff L is enumerable in Lexicographic order (alphabetic).
It is also known that context free language is a subset of recursive languages.
It is also known that context free language is a subset of recursive languages.
What is the minimum number of productions present in the below given context free grammar to make it Chomsky Normal Form?
S → XYx
X → xxy
Y → Xz- a)7
- b)8
- c)9
- d)10
Correct answer is option 'B'. Can you explain this answer?
What is the minimum number of productions present in the below given context free grammar to make it Chomsky Normal Form?
S → XYx
X → xxy
Y → Xz
S → XYx
X → xxy
Y → Xz
a)
7
b)
8
c)
9
d)
10
|
Eesha Bhat answered |
Concepts:
A context-free grammar is in Chomsky Normal Form if all productions are of the form
A → BC or A → a
{A, B, C} ϵ V and a ϵ T
V is variable(non-terminal) and a is terminal
A context-free grammar is in Chomsky Normal Form if all productions are of the form
A → BC or A → a
{A, B, C} ϵ V and a ϵ T
V is variable(non-terminal) and a is terminal
Calculation:
S → XA
A → YB
B → x
X → BC
C → BD
D → y
Y → XE
E → z
S → XA
A → YB
B → x
X → BC
C → BD
D → y
Y → XE
E → z
With reference to the process of conversion of a context free grammar to CNF, the number of variables to be introduced for the terminals are:
S->ABa
A->aab
B->Ac- a)3
- b)4
- c)2
- d)5
Correct answer is option 'A'. Can you explain this answer?
With reference to the process of conversion of a context free grammar to CNF, the number of variables to be introduced for the terminals are:
S->ABa
A->aab
B->Ac
S->ABa
A->aab
B->Ac
a)
3
b)
4
c)
2
d)
5
|
Amrutha Sengupta answered |
The number of variables to be introduced for the terminals in the conversion of a context-free grammar to Chomsky Normal Form (CNF) depends on the number of terminal symbols in the original grammar.
In CNF, each production rule is either of the form A → BC or A → a, where A, B, and C are variables and a is a terminal symbol.
To convert a terminal symbol to CNF, we introduce a new variable for each terminal symbol. Therefore, the number of variables to be introduced for the terminals is equal to the number of terminal symbols in the original grammar.
In CNF, each production rule is either of the form A → BC or A → a, where A, B, and C are variables and a is a terminal symbol.
To convert a terminal symbol to CNF, we introduce a new variable for each terminal symbol. Therefore, the number of variables to be introduced for the terminals is equal to the number of terminal symbols in the original grammar.
Let G be a grammar. When the production in G satisfy certain restrictions, then G is said to be in ___________- a)restricted form
- b)parsed form
- c)normal form
- d)all of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Let G be a grammar. When the production in G satisfy certain restrictions, then G is said to be in ___________
a)
restricted form
b)
parsed form
c)
normal form
d)
all of the mentioned
|
|
Bijoy Sharma answered |
Understanding Normal Forms in Grammar
In formal language theory, grammars can be classified based on their structure and the restrictions placed on their production rules. When a grammar meets specific criteria, it is referred to as being in *normal form*.
Types of Normal Forms
- Chomsky Normal Form (CNF):
- All production rules are of the form A → BC or A → a, where A, B, and C are non-terminal symbols and a is a terminal symbol.
- Greibach Normal Form (GNF):
- All production rules are of the form A → aα, where A is a non-terminal, a is a terminal, and α is a string of non-terminals (possibly empty).
Importance of Normal Forms
- Simplification:
- Normal forms simplify the parsing process, making it easier to analyze or implement parsing algorithms.
- Universality:
- Any context-free grammar can be converted into a normal form, ensuring that properties of the grammar remain intact.
Applications
- Compiler Design:
- Normal forms are essential in parsing techniques used in compiler design, ensuring the correct interpretation of programming languages.
- Automata Theory:
- They play a crucial role in the theoretical aspects of automata and formal languages, enabling a clearer understanding of language recognition.
In summary, when the productions in a grammar satisfy specific restrictions, the grammar is said to be in *normal form*. This classification is pivotal in computer science, especially in the fields of programming languages and compiler construction.
In formal language theory, grammars can be classified based on their structure and the restrictions placed on their production rules. When a grammar meets specific criteria, it is referred to as being in *normal form*.
Types of Normal Forms
- Chomsky Normal Form (CNF):
- All production rules are of the form A → BC or A → a, where A, B, and C are non-terminal symbols and a is a terminal symbol.
- Greibach Normal Form (GNF):
- All production rules are of the form A → aα, where A is a non-terminal, a is a terminal, and α is a string of non-terminals (possibly empty).
Importance of Normal Forms
- Simplification:
- Normal forms simplify the parsing process, making it easier to analyze or implement parsing algorithms.
- Universality:
- Any context-free grammar can be converted into a normal form, ensuring that properties of the grammar remain intact.
Applications
- Compiler Design:
- Normal forms are essential in parsing techniques used in compiler design, ensuring the correct interpretation of programming languages.
- Automata Theory:
- They play a crucial role in the theoretical aspects of automata and formal languages, enabling a clearer understanding of language recognition.
In summary, when the productions in a grammar satisfy specific restrictions, the grammar is said to be in *normal form*. This classification is pivotal in computer science, especially in the fields of programming languages and compiler construction.
The reduced grammar equivalent to the grammar, whose production rules are given below, isS → AB | CAB → BC | ABA → aC → a B | b- a)S → CA, A → a, C → b
- b)S → CA | B, B → BC | B, A → a, C → aB | b
- c)S → CA | B, B → BC, A → a, C → aB | b
- d)S → AB | AC, B → BC | BA, A → a, C → aB | b
Correct answer is option 'A'. Can you explain this answer?
The reduced grammar equivalent to the grammar, whose production rules are given below, is
S → AB | CA
B → BC | AB
A → a
C → a B | b
a)
S → CA, A → a, C → b
b)
S → CA | B, B → BC | B, A → a, C → aB | b
c)
S → CA | B, B → BC, A → a, C → aB | b
d)
S → AB | AC, B → BC | BA, A → a, C → aB | b
|
Luminary Institute answered |
S→AB |CA
B→BC |AB
A→a
C→aB | b
Here B is not derive any terminal string so remove productions contains B
S→CA
A→a
C→b
Hence above grammar is Reduced grammar.
Consider the languages L1 = {0i1j | i ≠ j}. L2 = {0i1j | i = j}. L3 = {0i1j | i = 2j + 1}. L4 = {0i1j | i ≠ 2j} Which one of the following statements is true?- a)Only L2 is context free
- b)Only L2 and L3 are context free
- c)Only L1 and L2 are context free
- d)All are context free
Correct answer is option 'D'. Can you explain this answer?
Consider the languages L1 = {0i1j | i ≠ j}. L2 = {0i1j | i = j}. L3 = {0i1j | i = 2j + 1}. L4 = {0i1j | i ≠ 2j} Which one of the following statements is true?
a)
Only L2 is context free
b)
Only L2 and L3 are context free
c)
Only L1 and L2 are context free
d)
All are context free
|
|
Eesha Bhat answered |
L1 = {0i1j | i ≠ j} → Context free
A regular expression for this is (0*1*)
A language that generates a regular expression is called regular language that is accepted by deterministic finite automata(DFA) can also be accepted by PDA
So, this language is also a context-free language
L2 = {0i1j | i = j} → Context free
First, push 0 into a stack then pop 0 for each 1 from the stack. The given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
L3 = {0i1j | i = 2j + 1} → Context free
If first 0 came then do nothing and for others 0's, for each zero push two 0's on the stack, and when 1 comes then pop two 0's for each 1 from the stack.
here pushing two 0's sounds non-deterministic but we push one symbol on the stack so it is deterministic
So, the given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
L4 = {0i1j | i ≠ 2j} → Context-free
let's take i = 2j +1
so it becomes as language L3
So, the given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
So, all the language are context-free
A regular expression for this is (0*1*)
A language that generates a regular expression is called regular language that is accepted by deterministic finite automata(DFA) can also be accepted by PDA
So, this language is also a context-free language
L2 = {0i1j | i = j} → Context free
First, push 0 into a stack then pop 0 for each 1 from the stack. The given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
L3 = {0i1j | i = 2j + 1} → Context free
If first 0 came then do nothing and for others 0's, for each zero push two 0's on the stack, and when 1 comes then pop two 0's for each 1 from the stack.
here pushing two 0's sounds non-deterministic but we push one symbol on the stack so it is deterministic
So, the given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
L4 = {0i1j | i ≠ 2j} → Context-free
let's take i = 2j +1
so it becomes as language L3
So, the given language is accepted by
Deterministic Pushdown Automaton. Therefore, L2 is deterministic context-free.
So, all the language are context-free
Consider the language L = {an |n ≥ 0} ∪ {anbn| n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?- a)I only
- b)II only
- c)I and III only
- d)III only
Correct answer is option 'C'. Can you explain this answer?
Consider the language L = {an |n ≥ 0} ∪ {anbn| n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k) for any k.
Which of the above statements is/are TRUE?
a)
I only
b)
II only
c)
I and III only
d)
III only
|
|
Sudhir Patel answered |
Statement I: TRUE.
L = {an |n ≥ 0} ∪ {anbn| n ≥ 0}
{an |n ≥ 0} is a regular language and {anbn| n ≥ 0} is a DCFL and hence, there Union would be a DCFL.
L = {an |n ≥ 0} ∪ {anbn| n ≥ 0}
{an |n ≥ 0} is a regular language and {anbn| n ≥ 0} is a DCFL and hence, there Union would be a DCFL.
Statement II: FALSE.
L is DCFL then it is CFL too.
L is DCFL then it is CFL too.
Statement III: TRUE
L cannot be LL(k) for any number of look-ahead. LL(k) cannot conclusively distinguish that whether the string to be parsed is from an or from anbn. Both have a common prefix.
L cannot be LL(k) for any number of look-ahead. LL(k) cannot conclusively distinguish that whether the string to be parsed is from an or from anbn. Both have a common prefix.
Let denote the languages generated by the grammar S→ 0S0 I 00.Which of the following is TRUE?- a)L=0+
- b)L is regular but not 0+
- c) L is context free but not regular
- d)L is not context free
Correct answer is 'B'. Can you explain this answer?
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
a)
L=0+
b)
L is regular but not 0+
c)
L is context free but not regular
d)
L is not context free
|
|
Avinash Mehta answered |
Explaining all the options:
Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0’s ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,…}, i.e only even no of 0’s ( excluding empty string}.
Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)
Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+.
Hence This option is Correct, because L is Regular but not 0+, as we proved above.
Which of the following languages can’t be accepted by a deterministic PDA?- a)The set of palindromes over alphabet {a, b}
- b)The set of all strings of balanced parenthesis
- c)L = {wcwRw in (0 + 1)*}
- d)L = {0n1n | n ≥ 0}
Correct answer is option 'A'. Can you explain this answer?
Which of the following languages can’t be accepted by a deterministic PDA?
a)
The set of palindromes over alphabet {a, b}
b)
The set of all strings of balanced parenthesis
c)
L = {wcwRw in (0 + 1)*}
d)
L = {0n1n | n ≥ 0}
|
Aditi Gupta answered |
Deterministic PDA can accept
(b) The set of all strings of balanced parenthesis.
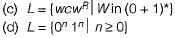
In each of the above the PDA can deterministically separate the push and pop operations,
But it cannot do the same in case (a), since it has to guess middle of palindrome, In DPDA we can’t do guesing, NPDA is required for this.
(b) The set of all strings of balanced parenthesis.
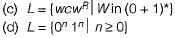
In each of the above the PDA can deterministically separate the push and pop operations,
But it cannot do the same in case (a), since it has to guess middle of palindrome, In DPDA we can’t do guesing, NPDA is required for this.
Which of the following is not true?- a)CFLs are closed under union and concatenation.
- b)Regular languages are closed under union and intersection.
- c)CFLs are not closed under intersection and complementation.
- d)If L is a CFL and R is a regular set then L ∩ R is not a CFL.
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not true?
a)
CFLs are closed under union and concatenation.
b)
Regular languages are closed under union and intersection.
c)
CFLs are not closed under intersection and complementation.
d)
If L is a CFL and R is a regular set then L ∩ R is not a CFL.
|
Krithika Kaur answered |
According to closure properties regular languages are closed under the ail finite basic operations like: 
But CFL is closed only under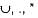
Also Regular inter section of CFL i.e. CFL intersected with regular language.
But CFL is closed only under
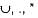
Also Regular inter section of CFL i.e. CFL intersected with regular language.
Ram and Shyam have been asked to show that a cartain problem II is NP-complete. Ram shows a polynomial time reduction from the 3-SAT problem to II and Shyam shows a polynomial time reduction from II to 3-SAT. Which of the following can be inferred from these reductions?- a)II is NP-hard but not NP-comp!ete
- b)II is NP-complete
- c)II is in NP, but is not NP-complete
- d)II is neither NP-hard, nor in NP
Correct answer is option 'B'. Can you explain this answer?
Ram and Shyam have been asked to show that a cartain problem II is NP-complete. Ram shows a polynomial time reduction from the 3-SAT problem to II and Shyam shows a polynomial time reduction from II to 3-SAT. Which of the following can be inferred from these reductions?
a)
II is NP-hard but not NP-comp!ete
b)
II is NP-complete
c)
II is in NP, but is not NP-complete
d)
II is neither NP-hard, nor in NP
|
|
Gitanjali Singh answered |
Since 3-SAT problem is NP-complete and 3-SAT is polynomial time reducible to π hence π is is also NP-complete.
If L1, is regular and L2 is CFL over ∑* which of the following statement is incorrect?- a) L1 ∪ L2 is CFL
- b)L1 ∩ L2 is regular
- c) L1* is regular
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If L1, is regular and L2 is CFL over ∑* which of the following statement is incorrect?
a)
L1 ∪ L2 is CFL
b)
L1 ∩ L2 is regular
c)
L1* is regular
d)
None of these
|
|
Hrishikesh Unni answered |
Since L1 and L2 are regular and context free languages respectively CFL are closed under regular ∪, ∩, therefore
(a) L1 ∪ L2 is CFL and therefore regular too.
(b) L1 ∩ L2 is not regular
(c) L1 * is regular
(a) L1 ∪ L2 is CFL and therefore regular too.
(b) L1 ∩ L2 is not regular
(c) L1 * is regular
Which of the following is/are FALSE regarding pumping lemma for regular languages?- a)Satisfying pumping lemma is a necessary condition for language to be regular
- b)Satisfying pumping lemma is a sufficient condition for language to be regular
- c)Not Satisfying pumping lemma is a necessary condition for language to be regular
- d)Not Satisfying pumping lemma is a sufficient condition for language to be not regular
Correct answer is option 'B,C'. Can you explain this answer?
Which of the following is/are FALSE regarding pumping lemma for regular languages?
a)
Satisfying pumping lemma is a necessary condition for language to be regular
b)
Satisfying pumping lemma is a sufficient condition for language to be regular
c)
Not Satisfying pumping lemma is a necessary condition for language to be regular
d)
Not Satisfying pumping lemma is a sufficient condition for language to be not regular
|
|
Anisha Chavan answered |
False Statements Regarding Pumping Lemma for Regular Languages:
b) Satisfying pumping lemma is a sufficient condition for a language to be regular.
The statement that satisfying the pumping lemma is a sufficient condition for a language to be regular is false. The pumping lemma is a necessary condition, but it is not sufficient. This means that if a language satisfies the pumping lemma, it may or may not be regular. The pumping lemma only guarantees that a language is not regular if it fails to satisfy the conditions of the lemma.
c) Not satisfying pumping lemma is a necessary condition for a language to be regular.
The statement that not satisfying the pumping lemma is a necessary condition for a language to be regular is also false. It is important to note that the pumping lemma can only be used to prove that a language is not regular. It cannot be used to prove that a language is regular. There are many regular languages that do not satisfy the pumping lemma, so the failure to satisfy the pumping lemma does not imply that a language is regular.
Explanation:
The pumping lemma for regular languages is a useful tool for proving that a language is not regular. It states that for any regular language L, there exists a constant p (the pumping length) such that any string s in L with length |s| ≥ p can be divided into three parts: s = xyz, satisfying the following conditions:
1. |xy| ≤ p: The length of xy (the first two parts of the string) is less than or equal to the pumping length.
2. |y| > 0: The length of y (the middle part of the string) is greater than zero.
3. For all i ≥ 0, the string xy^iz is also in L.
If a language fails to satisfy any of these conditions, it can be concluded that the language is not regular. However, it is important to note that satisfying the pumping lemma does not guarantee that a language is regular, as there are regular languages that do not satisfy the conditions of the pumping lemma.
In conclusion, the pumping lemma is a necessary condition for a language to be regular, but it is not sufficient. The failure to satisfy the pumping lemma does not necessarily imply that a language is regular. Therefore, options B and C are false statements regarding the pumping lemma for regular languages.
b) Satisfying pumping lemma is a sufficient condition for a language to be regular.
The statement that satisfying the pumping lemma is a sufficient condition for a language to be regular is false. The pumping lemma is a necessary condition, but it is not sufficient. This means that if a language satisfies the pumping lemma, it may or may not be regular. The pumping lemma only guarantees that a language is not regular if it fails to satisfy the conditions of the lemma.
c) Not satisfying pumping lemma is a necessary condition for a language to be regular.
The statement that not satisfying the pumping lemma is a necessary condition for a language to be regular is also false. It is important to note that the pumping lemma can only be used to prove that a language is not regular. It cannot be used to prove that a language is regular. There are many regular languages that do not satisfy the pumping lemma, so the failure to satisfy the pumping lemma does not imply that a language is regular.
Explanation:
The pumping lemma for regular languages is a useful tool for proving that a language is not regular. It states that for any regular language L, there exists a constant p (the pumping length) such that any string s in L with length |s| ≥ p can be divided into three parts: s = xyz, satisfying the following conditions:
1. |xy| ≤ p: The length of xy (the first two parts of the string) is less than or equal to the pumping length.
2. |y| > 0: The length of y (the middle part of the string) is greater than zero.
3. For all i ≥ 0, the string xy^iz is also in L.
If a language fails to satisfy any of these conditions, it can be concluded that the language is not regular. However, it is important to note that satisfying the pumping lemma does not guarantee that a language is regular, as there are regular languages that do not satisfy the conditions of the pumping lemma.
In conclusion, the pumping lemma is a necessary condition for a language to be regular, but it is not sufficient. The failure to satisfy the pumping lemma does not necessarily imply that a language is regular. Therefore, options B and C are false statements regarding the pumping lemma for regular languages.
Consider the following languages.
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?- a)L1 is regular and L2 is context-free.
- b)L1 is context-free but not regular and L2 is context-free.
- c)Neither L1 nor L2 is context-free.
- d)L1 is context-free but L2 is not context-free
Correct answer is option 'A'. Can you explain this answer?
Consider the following languages.
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
a)
L1 is regular and L2 is context-free.
b)
L1 is context-free but not regular and L2 is context-free.
c)
Neither L1 nor L2 is context-free.
d)
L1 is context-free but L2 is not context-free
|
|
Eesha Bhat answered |
Concept:
A language is regular if we could find a corresponding regular expression that generates it and an finite automata that accepts it. A language is CFL, if we could construct a Push Down Automata (PDA) that accepts it.
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L1 is a regular language.
Since it is given that w, x, y ϵ (0 + 1)+}, that means w, x, y all three can be strings of {0, 1}.
L1 can be generated by a regular expression of the form:
(0+1)+0 (0+1)+0 + (0+1)+1 (0+1)+1, by putting x as 0 and 1 alternatively. Since it can be represented as a regular expression, it is a regular language.
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
L2 is a Context Free Language.
L2 consists of set of strings which could be split into two non-identical substrings, but of equal length. Since comparison is involved, it cannot be done with a finite automata. However, a PDA can do comparisons, so PDA would accept the above language. Thus L2 is a CFL.
A language is regular if we could find a corresponding regular expression that generates it and an finite automata that accepts it. A language is CFL, if we could construct a Push Down Automata (PDA) that accepts it.
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L1 is a regular language.
Since it is given that w, x, y ϵ (0 + 1)+}, that means w, x, y all three can be strings of {0, 1}.
L1 can be generated by a regular expression of the form:
(0+1)+0 (0+1)+0 + (0+1)+1 (0+1)+1, by putting x as 0 and 1 alternatively. Since it can be represented as a regular expression, it is a regular language.
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
L2 is a Context Free Language.
L2 consists of set of strings which could be split into two non-identical substrings, but of equal length. Since comparison is involved, it cannot be done with a finite automata. However, a PDA can do comparisons, so PDA would accept the above language. Thus L2 is a CFL.
Referring to Turing Machine in previous question, what will be the output when the input is
I1 = 0100 and I2 = 0010?- a)I1 = 0 and I2 = Blank
- b)I1 = Blank and I2 = 0
- c)I1 = 1 and I2 = 1
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Referring to Turing Machine in previous question, what will be the output when the input is
I1 = 0100 and I2 = 0010?
I1 = 0100 and I2 = 0010?
a)
I1 = 0 and I2 = Blank
b)
I1 = Blank and I2 = 0
c)
I1 = 1 and I2 = 1
d)
None of the above
|
|
Anjali Saha answered |
Introduction:
In this question, we are given two inputs I1 and I2, which are binary strings. We need to determine the output of a Turing Machine when these inputs are given.
Explanation:
A Turing Machine is a theoretical model of a computing device that can manipulate symbols on a tape according to a set of rules. It has a tape with an infinite length divided into cells, each containing a symbol. The machine has a read/write head that can move left or right on the tape and read or write symbols on the cells.
Input:
I1 = 0100
I2 = 0010
Working of the Turing Machine:
1. Initially, the Turing Machine's read/write head is positioned at the leftmost cell of the tape, and the tape contains the input strings I1 and I2 separated by a blank symbol.
2. The machine starts by reading the first symbol of I1 and I2.
3. If the symbols at the current position are both 0, the machine moves to the right and continues to the next symbols.
4. If the symbol in I1 is 1 and the symbol in I2 is 0, the machine overwrites the symbol in I1 with a blank symbol and moves to the right.
5. If the symbol in I1 is 0 and the symbol in I2 is 1, the machine overwrites the symbol in I2 with a blank symbol and moves to the right.
6. If the symbol in I1 is 1 and the symbol in I2 is 1, the machine overwrites the symbol in I1 with a 0 and moves to the right.
7. The machine repeats steps 3-6 until it reaches the end of the input strings, indicated by a blank symbol.
8. After reaching the end of the input strings, the machine halts.
Output:
In this case, the machine will overwrite the symbols in I1 and I2 as follows:
1. Read the first symbol: 0 and 0
2. Move to the right
3. Read the second symbol: 1 and 0
4. Overwrite I1 with a blank symbol and move to the right
5. Read the third symbol: 0 and 1
6. Overwrite I2 with a blank symbol and move to the right
7. Read the fourth symbol: 0 and blank
8. The machine has reached the end of the input strings and halts.
Final Output:
After the machine halts, the symbols in I1 and I2 are as follows:
I1 = 0 and I2 = Blank
Therefore, the correct answer is option 'A' (I1 = 0 and I2 = Blank).
In this question, we are given two inputs I1 and I2, which are binary strings. We need to determine the output of a Turing Machine when these inputs are given.
Explanation:
A Turing Machine is a theoretical model of a computing device that can manipulate symbols on a tape according to a set of rules. It has a tape with an infinite length divided into cells, each containing a symbol. The machine has a read/write head that can move left or right on the tape and read or write symbols on the cells.
Input:
I1 = 0100
I2 = 0010
Working of the Turing Machine:
1. Initially, the Turing Machine's read/write head is positioned at the leftmost cell of the tape, and the tape contains the input strings I1 and I2 separated by a blank symbol.
2. The machine starts by reading the first symbol of I1 and I2.
3. If the symbols at the current position are both 0, the machine moves to the right and continues to the next symbols.
4. If the symbol in I1 is 1 and the symbol in I2 is 0, the machine overwrites the symbol in I1 with a blank symbol and moves to the right.
5. If the symbol in I1 is 0 and the symbol in I2 is 1, the machine overwrites the symbol in I2 with a blank symbol and moves to the right.
6. If the symbol in I1 is 1 and the symbol in I2 is 1, the machine overwrites the symbol in I1 with a 0 and moves to the right.
7. The machine repeats steps 3-6 until it reaches the end of the input strings, indicated by a blank symbol.
8. After reaching the end of the input strings, the machine halts.
Output:
In this case, the machine will overwrite the symbols in I1 and I2 as follows:
1. Read the first symbol: 0 and 0
2. Move to the right
3. Read the second symbol: 1 and 0
4. Overwrite I1 with a blank symbol and move to the right
5. Read the third symbol: 0 and 1
6. Overwrite I2 with a blank symbol and move to the right
7. Read the fourth symbol: 0 and blank
8. The machine has reached the end of the input strings and halts.
Final Output:
After the machine halts, the symbols in I1 and I2 are as follows:
I1 = 0 and I2 = Blank
Therefore, the correct answer is option 'A' (I1 = 0 and I2 = Blank).
he diagnoalization language, Ld is a- a)Recursive language.
- b)Recursive enumerable but not recursive
- c)Non-recurisvily - enumerable (non-RE) language
- d)Both (b) and (c)
Correct answer is option 'B'. Can you explain this answer?
he diagnoalization language, Ld is a
a)
Recursive language.
b)
Recursive enumerable but not recursive
c)
Non-recurisvily - enumerable (non-RE) language
d)
Both (b) and (c)
|
Soumya Desai answered |
The diagonalization language, Ld, is a language that cannot be enumerated by any Turing machine. In other words, there is no Turing machine that can generate a list of all the strings in Ld.
To understand why Ld is recursively enumerable but not recursive, let's break down the definitions of these terms:
1. Recursive language:
- A language is recursive if there exists a Turing machine that can halt and accept or reject any given input string.
- This means that for any input string, the Turing machine will always reach a final state and provide a definite answer (accept or reject).
2. Recursive enumerable language:
- A language is recursively enumerable if there exists a Turing machine that can enumerate (list) all the strings in the language.
- This means that for any string in the language, the Turing machine will eventually generate it.
- However, the Turing machine may not halt or generate any output for strings that are not in the language.
Now, let's analyze Ld:
- Ld is the language that contains all the binary strings that do not belong to themselves. In other words, for any string x, x is in Ld if and only if x is not in the language described by the xth Turing machine.
- Assume that there exists a Turing machine TMd that can enumerate all the strings in Ld. This means that TMd can generate a list of all the binary strings that do not belong to themselves.
- Now, let's construct a contradiction by considering a new string d, which is the description of a Turing machine that behaves differently than all the Turing machines in the list generated by TMd.
- Since d is different from every Turing machine in the list, it must either belong to Ld or not. However, both possibilities lead to a contradiction:
1. If d is in Ld, it means that d does not belong to itself. But since d is different from all the machines in the list, it must belong to itself. This is a contradiction.
2. If d is not in Ld, it means that d belongs to itself. But again, since d is different from all the machines in the list, it must not belong to itself. This is also a contradiction.
The contradiction arises from assuming the existence of TMd, which means that no Turing machine can enumerate all the strings in Ld. Therefore, Ld is recursively enumerable but not recursive.
To understand why Ld is recursively enumerable but not recursive, let's break down the definitions of these terms:
1. Recursive language:
- A language is recursive if there exists a Turing machine that can halt and accept or reject any given input string.
- This means that for any input string, the Turing machine will always reach a final state and provide a definite answer (accept or reject).
2. Recursive enumerable language:
- A language is recursively enumerable if there exists a Turing machine that can enumerate (list) all the strings in the language.
- This means that for any string in the language, the Turing machine will eventually generate it.
- However, the Turing machine may not halt or generate any output for strings that are not in the language.
Now, let's analyze Ld:
- Ld is the language that contains all the binary strings that do not belong to themselves. In other words, for any string x, x is in Ld if and only if x is not in the language described by the xth Turing machine.
- Assume that there exists a Turing machine TMd that can enumerate all the strings in Ld. This means that TMd can generate a list of all the binary strings that do not belong to themselves.
- Now, let's construct a contradiction by considering a new string d, which is the description of a Turing machine that behaves differently than all the Turing machines in the list generated by TMd.
- Since d is different from every Turing machine in the list, it must either belong to Ld or not. However, both possibilities lead to a contradiction:
1. If d is in Ld, it means that d does not belong to itself. But since d is different from all the machines in the list, it must belong to itself. This is a contradiction.
2. If d is not in Ld, it means that d belongs to itself. But again, since d is different from all the machines in the list, it must not belong to itself. This is also a contradiction.
The contradiction arises from assuming the existence of TMd, which means that no Turing machine can enumerate all the strings in Ld. Therefore, Ld is recursively enumerable but not recursive.
Which of the following languages are context free ?
L1 = {aibj ck | i< j < k}
L2 = {am bn | m≠n and m ≠2n}- a)Only L1
- b)Only L2
- c)Both L1 and L2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Which of the following languages are context free ?
L1 = {aibj ck | i< j < k}
L2 = {am bn | m≠n and m ≠2n}
L1 = {aibj ck | i< j < k}
L2 = {am bn | m≠n and m ≠2n}
a)
Only L1
b)
Only L2
c)
Both L1 and L2
d)
None of these
|
|
Eesha Bhat answered |
L1 = {aibj ck | i < j < k} is not context free
We can prove this using the pumping lemma also let pumping constant = n
String S = an bn+1 cn+2∈L
Let S = uvwxy where |vx| ≥1 and |vwx| ≤n
We can prove this using the pumping lemma also let pumping constant = n
String S = an bn+1 cn+2∈L
Let S = uvwxy where |vx| ≥1 and |vwx| ≤n
Cases :
- vwx is in an : for i = 2, S1 = uviwxiy has more or equal a’s than b’s ⇒ S1∉L
- vwx is in bn : for i = 0, S1 = uviwxiy has more or equal a’s than b’s ⇒ S1∉ L
- vwx is in cn : for i = 0, S1 = uviwxiy has more or equal b’s than c’s ⇒ S1∉ L
- vwx contains both a and b i.e. an bn+1 :
- Since x has atleast one b, for i = 2, S1 = uviwxiy has more b’s than c’s ⇒ S1∉ L
- vwx contains both b and c i.e. bn+1 cn+2 since v has atleast one b, for i = 0,
S1 = uviwxi y has more or equal a’s than b’s ⇒ S1∉ L
So we can say that by pumping lemma, given language is not CFL.
L2 = {am bn | m ≠n and m ≠2n} is CFL
L2 can be define as L21 = {am bn | m < n}
L22 = {am bn | n < m < 2n}
L23 = {am bn | m > 2n}
So, L2 = L21∪L22∪L23
As there exists CFGs for L21, L22 and L23 and since union of CFL’s is a CFL. Thus L2 is CFL.
So we can say that by pumping lemma, given language is not CFL.
L2 = {am bn | m ≠n and m ≠2n} is CFL
L2 can be define as L21 = {am bn | m < n}
L22 = {am bn | n < m < 2n}
L23 = {am bn | m > 2n}
So, L2 = L21∪L22∪L23
As there exists CFGs for L21, L22 and L23 and since union of CFL’s is a CFL. Thus L2 is CFL.
Let G = (V, T, S, P) be any context-free grammar without any λ-productions or unit productions. Let K be the maximum number of symbols on the right of any production in P. The maximum number of production rules for any equivalent grammar in Chomsky normal form is given by:
Where |⋅| denotes the cardinality of the set.- a)(K - 1)|P| + |T| -1
- b)(K - 1)|P| + |T|
- c)K |P| + |T| -1
- d)K |P| + |T|
Correct answer is option 'B'. Can you explain this answer?
Let G = (V, T, S, P) be any context-free grammar without any λ-productions or unit productions. Let K be the maximum number of symbols on the right of any production in P. The maximum number of production rules for any equivalent grammar in Chomsky normal form is given by:
Where |⋅| denotes the cardinality of the set.
Where |⋅| denotes the cardinality of the set.
a)
(K - 1)|P| + |T| -1
b)
(K - 1)|P| + |T|
c)
K |P| + |T| -1
d)
K |P| + |T|
|
|
Shail Kulkarni answered |
Restrictions on the production rules.
1. V is a finite set of variables or non-terminals.
2. T is a finite set of terminals.
3. S is the start symbol, which is a member of V.
4. P is a finite set of production rules, where each rule has the form A -> α, where A is a variable in V, and α is a string of variables and terminals in (V ∪ T)*.
Here, V represents the set of variables or non-terminals in the grammar, which are placeholders that can be replaced by strings of terminals and variables. T represents the set of terminals, which are the actual symbols in the language defined by the grammar. S is the start symbol, which is the initial variable or non-terminal from which the language can be derived. P represents the set of production rules, which define how variables can be replaced by other variables and terminals.
A context-free grammar without any restrictions on the production rules means that any variable can be replaced by any string of terminals and variables. This allows for more flexibility in defining the language and generating strings that belong to the language. However, it also means that the grammar might generate ambiguous or infinite languages, which can make parsing and understanding the language more difficult.
1. V is a finite set of variables or non-terminals.
2. T is a finite set of terminals.
3. S is the start symbol, which is a member of V.
4. P is a finite set of production rules, where each rule has the form A -> α, where A is a variable in V, and α is a string of variables and terminals in (V ∪ T)*.
Here, V represents the set of variables or non-terminals in the grammar, which are placeholders that can be replaced by strings of terminals and variables. T represents the set of terminals, which are the actual symbols in the language defined by the grammar. S is the start symbol, which is the initial variable or non-terminal from which the language can be derived. P represents the set of production rules, which define how variables can be replaced by other variables and terminals.
A context-free grammar without any restrictions on the production rules means that any variable can be replaced by any string of terminals and variables. This allows for more flexibility in defining the language and generating strings that belong to the language. However, it also means that the grammar might generate ambiguous or infinite languages, which can make parsing and understanding the language more difficult.
Context-free language can be recognized by- a)Finite state automaton.
- b)Linear bounded automata
- c)Push down automata
- d)Both (b) and (c) above
Correct answer is option 'D'. Can you explain this answer?
Context-free language can be recognized by
a)
Finite state automaton.
b)
Linear bounded automata
c)
Push down automata
d)
Both (b) and (c) above
|
|
Garima Dasgupta answered |
Since the power of recognization of NFA is less then the PDA. Also CFL can be recognized by the one which has equal or higher power than the PDA. Both PDA and LBA can recognize the CFL.
Let L be a regular language and M be a context-free language, both over the alphabet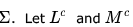 
denote the complements of L and M respectively. Which of the following statements about the language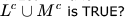 
- a)It is necessarily regular but not necessarily context-free.
- b)It is necessarily context-free.
- c)It is necessarily non-regular.
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Let L be a regular language and M be a context-free language, both over the alphabet 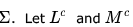denote the complements of L and M respectively. Which of the following statements about the language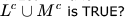
denote the complements of L and M respectively. Which of the following statements about the language a)
It is necessarily regular but not necessarily context-free.
b)
It is necessarily context-free.
c)
It is necessarily non-regular.
d)
None of the above
|
Anirban Khanna answered |
Proposition:
L is a regular language
M is a context free language
Derivation:
L_c union M_c = complement{L intersection M}
Now, L intersection M is a CFL according to closure laws of CFLs, i.e. intersection of a CFL with RL is always a CFL.
But, complement{L intersection M} might not be a CFL because complement over CFL doesn’t guarantee a CFL. It can even be a RL or it might even lie outside the CFL circle. It will be a context-sensitive language certainly, but nothing else can be said about it.
Conclusion:
Considering the above derivation, none of the statements are true. Hence correct answer would be (D) None of the above.
The language accepted by a Pushdown Automaton in which the stack is limited to 10 items is best described as- a)Context free
- b)Regular
- c)Deterministic Context free
- d)Recursive
Correct answer is option 'B'. Can you explain this answer?
The language accepted by a Pushdown Automaton in which the stack is limited to 10 items is best described as
a)
Context free
b)
Regular
c)
Deterministic Context free
d)
Recursive
|
|
Rajeev Menon answered |
Pushdown automata is used for context free languages, i.e., languages in which the length of elements is unrestricted and length of one element is related to other. To resolve this problem, we use a stack with no restrictions on length.
But in the given case, length of stack is restricted. Thus, this pushdown automata can only accept languages which can also be accepted by finite state automata and a finite state automata accepts only regular languages.
Which of the following statement is correct?- a)All Regular grammar are context free but not vice versa
- b)All context free grammar are regular grammar but not vice versa
- c)Regular grammar and context free grammar are the same entity
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Which of the following statement is correct?
a)
All Regular grammar are context free but not vice versa
b)
All context free grammar are regular grammar but not vice versa
c)
Regular grammar and context free grammar are the same entity
d)
None of the mentioned
|
|
Swati Kaur answered |
Regular Grammar and Context-Free Grammar
Regular grammar and context-free grammar are two types of formal grammars used in computer science and linguistics. While they share similarities, there are also significant differences between the two.
Regular Grammar
A regular grammar is a type of formal grammar that generates regular languages. A regular language is a language that can be recognized by a finite automaton, such as a deterministic finite automaton (DFA) or a non-deterministic finite automaton (NFA).
Regular grammar is defined by a set of production rules of the form:
A → aB or A → a
where A and B are non-terminal symbols, a is a terminal symbol, and the arrow → denotes a production rule.
Context-Free Grammar
A context-free grammar is a type of formal grammar that generates context-free languages. A context-free language is a language that can be recognized by a pushdown automaton (PDA).
Context-free grammar is defined by a set of production rules of the form:
A → α
where A is a non-terminal symbol and α is a string of terminal and/or non-terminal symbols.
Comparison
While both regular grammar and context-free grammar are types of formal grammars, there are significant differences between the two:
- Regular grammar generates regular languages, while context-free grammar generates context-free languages.
- Regular grammar is defined by a set of production rules of the form A → aB or A → a, while context-free grammar is defined by a set of production rules of the form A → α.
- Regular grammar is a subset of context-free grammar, meaning that all regular grammars are also context-free grammars. However, not all context-free grammars are regular grammars.
Conclusion
In summary, the correct statement is that all regular grammars are context-free but not vice versa. This is because regular grammar is a subset of context-free grammar, meaning that every regular grammar is also a context-free grammar. However, not every context-free grammar is a regular grammar, as context-free languages can be more complex than regular languages.
Regular grammar and context-free grammar are two types of formal grammars used in computer science and linguistics. While they share similarities, there are also significant differences between the two.
Regular Grammar
A regular grammar is a type of formal grammar that generates regular languages. A regular language is a language that can be recognized by a finite automaton, such as a deterministic finite automaton (DFA) or a non-deterministic finite automaton (NFA).
Regular grammar is defined by a set of production rules of the form:
A → aB or A → a
where A and B are non-terminal symbols, a is a terminal symbol, and the arrow → denotes a production rule.
Context-Free Grammar
A context-free grammar is a type of formal grammar that generates context-free languages. A context-free language is a language that can be recognized by a pushdown automaton (PDA).
Context-free grammar is defined by a set of production rules of the form:
A → α
where A is a non-terminal symbol and α is a string of terminal and/or non-terminal symbols.
Comparison
While both regular grammar and context-free grammar are types of formal grammars, there are significant differences between the two:
- Regular grammar generates regular languages, while context-free grammar generates context-free languages.
- Regular grammar is defined by a set of production rules of the form A → aB or A → a, while context-free grammar is defined by a set of production rules of the form A → α.
- Regular grammar is a subset of context-free grammar, meaning that all regular grammars are also context-free grammars. However, not all context-free grammars are regular grammars.
Conclusion
In summary, the correct statement is that all regular grammars are context-free but not vice versa. This is because regular grammar is a subset of context-free grammar, meaning that every regular grammar is also a context-free grammar. However, not every context-free grammar is a regular grammar, as context-free languages can be more complex than regular languages.
Regular grammar is - a)non context free grammar
- b)english grammar
- c)none of the mentioned
- d)context free grammar
Correct answer is option 'D'. Can you explain this answer?
Regular grammar is
a)
non context free grammar
b)
english grammar
c)
none of the mentioned
d)
context free grammar
|
|
Ananya Shah answered |
Understanding Regular Grammar
Regular grammar is a formal grammar that is used to define regular languages, which can be recognized by finite automata. The key characteristics of regular grammar are essential for distinguishing it from other types of grammars.
Key Characteristics of Regular Grammar:
- Definition: Regular grammar comprises productions where the left-hand side consists of a single non-terminal symbol, and the right-hand side can be either a terminal symbol or a terminal symbol followed by a non-terminal symbol.
- Types: There are two types of regular grammars: right-linear and left-linear. In right-linear grammars, the non-terminal appears at the right end of the production, while in left-linear grammars, it appears at the left end.
- Language Recognition: Regular grammars generate languages that can be recognized by finite state machines. This means that the languages they produce have a limited structural complexity.
Comparison with Context-Free Grammar:
- Context-Free Grammar (CFG): This is a more powerful type of grammar that allows for productions where the left-hand side can be a single non-terminal and the right-hand side can be a string of terminals and non-terminals. CFGs can describe languages that require a stack for recognition, such as balanced parentheses.
- Inclusion: All regular languages are also context-free, meaning that regular grammars are a subset of context-free grammars. However, not all context-free grammars are regular.
Conclusion:
Given these characteristics and relationships, the correct answer to the question is option 'D' - "context-free grammar." Regular grammar is indeed a specific form of context-free grammar that captures simpler structures within formal language theory.
Regular grammar is a formal grammar that is used to define regular languages, which can be recognized by finite automata. The key characteristics of regular grammar are essential for distinguishing it from other types of grammars.
Key Characteristics of Regular Grammar:
- Definition: Regular grammar comprises productions where the left-hand side consists of a single non-terminal symbol, and the right-hand side can be either a terminal symbol or a terminal symbol followed by a non-terminal symbol.
- Types: There are two types of regular grammars: right-linear and left-linear. In right-linear grammars, the non-terminal appears at the right end of the production, while in left-linear grammars, it appears at the left end.
- Language Recognition: Regular grammars generate languages that can be recognized by finite state machines. This means that the languages they produce have a limited structural complexity.
Comparison with Context-Free Grammar:
- Context-Free Grammar (CFG): This is a more powerful type of grammar that allows for productions where the left-hand side can be a single non-terminal and the right-hand side can be a string of terminals and non-terminals. CFGs can describe languages that require a stack for recognition, such as balanced parentheses.
- Inclusion: All regular languages are also context-free, meaning that regular grammars are a subset of context-free grammars. However, not all context-free grammars are regular.
Conclusion:
Given these characteristics and relationships, the correct answer to the question is option 'D' - "context-free grammar." Regular grammar is indeed a specific form of context-free grammar that captures simpler structures within formal language theory.
Time taken by one tape TM to simulate n moves of k-tape TM is- a)O(n)
- b)0(nk)
- c)O(n2)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Time taken by one tape TM to simulate n moves of k-tape TM is
a)
O(n)
b)
0(nk)
c)
O(n2)
d)
None of these
|
|
Swati Kaur answered |
Single tape turing machine can simulate n-moves of k-tape TM in O(n2).
Let ∑ = {a, b}, r1 = a(a + b)* and r2 = b(a + b)*. Which of the following is true?- a)L(r1) = L(r2) = ∑*
- b)L(r1) ∩ L (r2) = {∈}
- c)L(r1) ∪ L(r2) = ∑*
- d)L(r1) ∪ L(r2) ∪ {∈} = ∑*
Correct answer is option 'D'. Can you explain this answer?
Let ∑ = {a, b}, r1 = a(a + b)* and r2 = b(a + b)*. Which of the following is true?
a)
L(r1) = L(r2) = ∑*
b)
L(r1) ∩ L (r2) = {∈}
c)
L(r1) ∪ L(r2) = ∑*
d)
L(r1) ∪ L(r2) ∪ {∈} = ∑*
|
Krish Datta answered |
L(r1) is the set of all string starting with ‘a’.
L(r2) is the set of all starting with ‘b’.
Since any word belonging to ∑* either starts with “ a ” or starts with " b ” or is “∈ ” , therefore
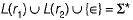
L(r2) is the set of all starting with ‘b’.
Since any word belonging to ∑* either starts with “ a ” or starts with " b ” or is “∈ ” , therefore
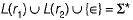
To derive the string length 4, How many minimum productions are required for Chomsky normal form ?
Correct answer is '7'. Can you explain this answer?
To derive the string length 4, How many minimum productions are required for Chomsky normal form ?
|
|
Garima Bose answered |
Chomsky Normal Form (CNF)
Chomsky Normal Form (CNF) is a way to represent a context-free grammar in a simplified form. In CNF, all production rules have the following forms:
1. A -> BC (Binary Rule)
2. A -> a (Terminal Rule)
Where A, B, and C are non-terminal symbols, and a is a terminal symbol.
Finding the Minimum Productions for Length 4
To derive a string of length 4 in Chomsky Normal Form, we need to consider all possible combinations of binary and terminal rules. Let's break down the process step by step:
Step 1: Start by introducing the initial non-terminal symbol S.
Step 2: Generate all possible combinations of binary and terminal rules to derive a string of length 4.
We can represent the length 4 string as follows:
S -> AB
A -> BC
B -> CD
C -> DE
Here, each non-terminal symbol represents a length 1 string. By chaining the non-terminal symbols together, we can derive a string of length 4.
Step 3: Finally, we convert the grammar to Chomsky Normal Form by eliminating unit rules and long rules.
In our case, there are no unit rules or long rules, so we don't need to perform any further conversions.
Calculating the Minimum Productions
To calculate the minimum number of productions, we count the number of binary and terminal rules used in the derivation.
In our case, we have used 4 binary rules and 3 terminal rules, resulting in a total of 7 productions.
Therefore, the correct answer is '7'.
Summary
To derive a string of length 4 in Chomsky Normal Form, we need a minimum of 7 productions. This involves introducing the initial non-terminal symbol, generating all possible combinations of binary and terminal rules, and converting the grammar to Chomsky Normal Form if necessary. By following these steps, we can obtain the desired string length while adhering to the rules of CNF.
Chomsky Normal Form (CNF) is a way to represent a context-free grammar in a simplified form. In CNF, all production rules have the following forms:
1. A -> BC (Binary Rule)
2. A -> a (Terminal Rule)
Where A, B, and C are non-terminal symbols, and a is a terminal symbol.
Finding the Minimum Productions for Length 4
To derive a string of length 4 in Chomsky Normal Form, we need to consider all possible combinations of binary and terminal rules. Let's break down the process step by step:
Step 1: Start by introducing the initial non-terminal symbol S.
Step 2: Generate all possible combinations of binary and terminal rules to derive a string of length 4.
We can represent the length 4 string as follows:
S -> AB
A -> BC
B -> CD
C -> DE
Here, each non-terminal symbol represents a length 1 string. By chaining the non-terminal symbols together, we can derive a string of length 4.
Step 3: Finally, we convert the grammar to Chomsky Normal Form by eliminating unit rules and long rules.
In our case, there are no unit rules or long rules, so we don't need to perform any further conversions.
Calculating the Minimum Productions
To calculate the minimum number of productions, we count the number of binary and terminal rules used in the derivation.
In our case, we have used 4 binary rules and 3 terminal rules, resulting in a total of 7 productions.
Therefore, the correct answer is '7'.
Summary
To derive a string of length 4 in Chomsky Normal Form, we need a minimum of 7 productions. This involves introducing the initial non-terminal symbol, generating all possible combinations of binary and terminal rules, and converting the grammar to Chomsky Normal Form if necessary. By following these steps, we can obtain the desired string length while adhering to the rules of CNF.
Context-free languages and regular languages are both closed under the operations(s) of
(i) Union
(ii) Intersection
(iii) Concatenation- a)(i) and (ii) only
- b)(ii) and (iii) only
- c)(i) and (iii) only
- d)All of these
Correct answer is option 'C'. Can you explain this answer?
Context-free languages and regular languages are both closed under the operations(s) of
(i) Union
(ii) Intersection
(iii) Concatenation
(i) Union
(ii) Intersection
(iii) Concatenation
a)
(i) and (ii) only
b)
(ii) and (iii) only
c)
(i) and (iii) only
d)
All of these
|
|
Yashvi Das answered |
Regular and context free languages are both closed under union and concatenation while only regular is closed under intersection.
If L1 is context free language and L2 is a regular language which of the following is/are false?
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular- a)Both a and c
- b) Both b and c
- c)Only b
- d)Only c
Correct answer is option 'A'. Can you explain this answer?
If L1 is context free language and L2 is a regular language which of the following is/are false?
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
a) L1-L2 is not context free
b) L1 ∩ L2 is context free
c) ~L1 is context free
d) ~L2 is regular
a)
Both a and c
b)
Both b and c
c)
Only b
d)
Only c
|
Kabir Verma answered |
- Given L1 is a context free language and L2 as a regular language then L1-L2 is context free language and
- ~L1(complement of context free) is not context free because context free is not closed under complement.
- Complement of regular language i.e. ~L2 is also regular ( so d is correct ) since statements a and c are false.
Hence,Option (C) is correct.
Pumping lemma for regular language is generally used for proving :- a)whether two given regular expressions are equivalent
- b)a given grammar is ambiguous
- c)a given grammar is regular
- d)a given grammar is not regular
Correct answer is option 'D'. Can you explain this answer?
Pumping lemma for regular language is generally used for proving :
a)
whether two given regular expressions are equivalent
b)
a given grammar is ambiguous
c)
a given grammar is regular
d)
a given grammar is not regular
|
|
Riverdale Learning Institute answered |
The pumping lemma is often used to prove that a particular language is non-regular. Pumping lemma for regular language is generally used for proving a given grammar is not regular.
Hence the correct answer is a given grammar is not regular.
Hence the correct answer is a given grammar is not regular.
If L1 and L2 are a pair of complementary languages. Which of the following statement is not possible?- a)Both L1, and L2 are recursive.
- b)L1 is recursive and L2 is recursively enumerable but not a recursive.
- c)Neither L1, nor L2 is recursively enumerable.
- d)One is recursively enumerable but not recursive, the other is is not recursively enumberable.
Correct answer is option 'B'. Can you explain this answer?
If L1 and L2 are a pair of complementary languages. Which of the following statement is not possible?
a)
Both L1, and L2 are recursive.
b)
L1 is recursive and L2 is recursively enumerable but not a recursive.
c)
Neither L1, nor L2 is recursively enumerable.
d)
One is recursively enumerable but not recursive, the other is is not recursively enumberable.
|
Devansh Chavan answered |
The correct statement follows from following theorem:
Theorem: If L1 and L2 is a pair of complementary language then either
• Both L1 and L2 are recursive.
• Neither L1, and L2 are recursively enumerable.
• One is recursively enumerable but not recursive, the other is not RE.
Option (b) is not possible, since if L1 is recursive, then
will also be recursive.
Theorem: If L1 and L2 is a pair of complementary language then either
• Both L1 and L2 are recursive.
• Neither L1, and L2 are recursively enumerable.
• One is recursively enumerable but not recursive, the other is not RE.
Option (b) is not possible, since if L1 is recursive, then
will also be recursive.For S->0S1|e for ∑={0,1}*, which of the following is wrong for the language produced?- a)Non regular language
- b)0n1n | n > = 0
- c)0n1n | n > = 1
- d)None of the mentioned
Correct answer is option 'D'. Can you explain this answer?
For S->0S1|e for ∑={0,1}*, which of the following is wrong for the language produced?
a)
Non regular language
b)
0n1n | n > = 0
c)
0n1n | n > = 1
d)
None of the mentioned
|
|
Sudhir Patel answered |
L = {e, 01, 0011, 000111, ……0n1n}. As epsilon is a part of the set, thus all the options are correct implying none of them to be wrong.
r1 = {b* ab* ab* ab*)*, r2 = (b* ab* ab*)*. What is L(r1) ∩ L(r2)?- a)[(b* ab* ab* ab*)*]
- b)[(b* ab* ab*)*]
- c)[(if ab* a b*)6]
- d)[(b* ab* ab* ab* ab* ab* ab*)*]
Correct answer is option 'D'. Can you explain this answer?
r1 = {b* ab* ab* ab*)*, r2 = (b* ab* ab*)*. What is L(r1) ∩ L(r2)?
a)
[(b* ab* ab* ab*)*]
b)
[(b* ab* ab*)*]
c)
[(if ab* a b*)6]
d)
[(b* ab* ab* ab* ab* ab* ab*)*]
|
Naina Sharma answered |
r1, denotes multiple of 3 a’s, with any number of b’s.
r2 denotes multiple of 2 a’s, with any number of b’s. L(r1) ∩ L(r2) denotes multiple of 6 a’s, with any number of b’s. Hence,
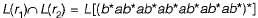
A CFG (Context Free Grammar) is said to be in Chomsky Normal Form (CNF), if all the productions are of the form A → BC or A → a. Let G be a CFG in CNF. To derive a string of terminals of length x, the number of products to be used is- a)2x - 1
- b)2x
- c)2x + 1
- d)2
Correct answer is option 'A'. Can you explain this answer?
A CFG (Context Free Grammar) is said to be in Chomsky Normal Form (CNF), if all the productions are of the form A → BC or A → a. Let G be a CFG in CNF. To derive a string of terminals of length x, the number of products to be used is
a)
2x - 1
b)
2x
c)
2x + 1
d)
2
|
|
Eesha Bhat answered |
Concept:
A context-free grammar is in Chomsky Normal Form if all productions are of the form
A → BC or A → a
{A, B, C} ϵ V and a ϵ T
V is variable(non-terminal) and a is terminal
A context-free grammar is in Chomsky Normal Form if all productions are of the form
A → BC or A → a
{A, B, C} ϵ V and a ϵ T
V is variable(non-terminal) and a is terminal
Formula:
n = 2x - 1
number of productions required to generates string of length x.
where x is the length of the string
n = 2x - 1
number of productions required to generates string of length x.
where x is the length of the string
Production:
S → XY
X → a
Y → b
Derive the string ab
S → XY
S → aY
S → ab
Number of productions needed = 3
Verification
2x - 1 = 2(2) - 1 = 3
S → XY
X → a
Y → b
Derive the string ab
S → XY
S → aY
S → ab
Number of productions needed = 3
Verification
2x - 1 = 2(2) - 1 = 3
Consider G = {(a, b), {S}, S, |S→b|Sa|aS|SS}) Which of the following are true?
(i) aabbaa ∈ G
(ii) G is ambiguous
(iii) Regular expression corresponding to G is ba*- a)(i) and (ii) only
- b)(ii) and (iii) only
- c)(i) and (iii) only
- d)all of the above
Correct answer is option 'A'. Can you explain this answer?
Consider G = {(a, b), {S}, S, |S→b|Sa|aS|SS}) Which of the following are true?
(i) aabbaa ∈ G
(ii) G is ambiguous
(iii) Regular expression corresponding to G is ba*
(i) aabbaa ∈ G
(ii) G is ambiguous
(iii) Regular expression corresponding to G is ba*
a)
(i) and (ii) only
b)
(ii) and (iii) only
c)
(i) and (iii) only
d)
all of the above
|
Bibek Choudhary answered |
Two derivation trees are possible for aabba as given below:
Therefore (i) and (ii) are both true.
Choice (iii): ‘aba’ is also accepted by the given grammar. Therefore (iii) is false.
Therefore (i) and (ii) are both true.
Choice (iii): ‘aba’ is also accepted by the given grammar. Therefore (iii) is false.
A PDA behaves like a TM when the number of auxiliary memory it has, is- a)0
- b)1 or more
- c)2 or more
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A PDA behaves like a TM when the number of auxiliary memory it has, is
a)
0
b)
1 or more
c)
2 or more
d)
None of these
|
Advait Shah answered |
Auxiliary memory = memory used by the machine for calculations or swappings.
PDA with 2 or more stacks is equivalent to TM.
PDA with 2 or more stacks is equivalent to TM.
Which of the following statements are true?
(i) The complement of a language is always regular.
(ii) The intersection of regular languages is regular.
(iii) The complement of a regular language is regular.- a)(i) and (ii) only
- b)(ii) and (iii) only
- c)(i) and (iii) only
- d)All of these
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements are true?
(i) The complement of a language is always regular.
(ii) The intersection of regular languages is regular.
(iii) The complement of a regular language is regular.
(i) The complement of a language is always regular.
(ii) The intersection of regular languages is regular.
(iii) The complement of a regular language is regular.
a)
(i) and (ii) only
b)
(ii) and (iii) only
c)
(i) and (iii) only
d)
All of these
|
|
Maitri Bose answered |
According to the closure properties regular language is closed under union, intersection, Kleen closure, concatenation, complementation. But the complementation of any language need not to be always regular.
Which among the following cannot be accepted by a regular grammar?- a)L is a set of numbers divisible by 2
- b)L is a set of binary complement
- c)L is a set of string with odd number of 0
- d)L is a set of 0n1n
Correct answer is option 'D'. Can you explain this answer?
Which among the following cannot be accepted by a regular grammar?
a)
L is a set of numbers divisible by 2
b)
L is a set of binary complement
c)
L is a set of string with odd number of 0
d)
L is a set of 0n1n
|
|
Sudhir Patel answered |
There exists no finite automata to accept the given language i.e. 0n1n. For other options, it is possible to make a dfa or nfa representing the language set.
A countable union of countable sets is not- a)Countable
- b)Uncountable
- c)Countably infinite
- d)Denumerable
Correct answer is option 'B'. Can you explain this answer?
A countable union of countable sets is not
a)
Countable
b)
Uncountable
c)
Countably infinite
d)
Denumerable
|
|
Maitri Bose answered |
A countable union of countable set is countable. Countably infinite and denumerable are alternate names of countable sets.
Every grammar in Chomsky Normal Form is:- a)regular
- b)context sensitive
- c)context free
- d)all of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Every grammar in Chomsky Normal Form is:
a)
regular
b)
context sensitive
c)
context free
d)
all of the mentioned
|
|
Yash Verma answered |
Chomsky Normal Form (CNF) is a specific form of grammar that is commonly used in computer science and linguistics. It is named after the renowned linguist Noam Chomsky, who introduced this form of grammar in the 1950s. CNF has certain characteristics that set it apart from other forms of grammar, such as regular grammar and context-sensitive grammar.
Chomsky Normal Form (CNF)
--------------------------
Chomsky Normal Form (CNF) is a type of context-free grammar (CFG) that has the following properties:
1. Every production rule is of the form A -> BC or A -> a, where A, B, and C are non-terminal symbols, and a is a terminal symbol.
2. The start symbol S does not appear on the right-hand side of any production rule, except for the rule S -> ε, where ε represents the empty string.
In CNF, each production rule either produces two non-terminal symbols or a non-terminal symbol and a terminal symbol. This form simplifies the derivation process and allows for more efficient parsing algorithms.
Explanation of the Answer
--------------------------
The correct answer to the question is "C) context-free." This means that every grammar in Chomsky Normal Form is a context-free grammar (CFG). Here's why:
1. Regular Grammar (Option A): Regular grammars have production rules of the form A -> aB or A -> a, where A and B are non-terminals, and a is a terminal symbol. In CNF, the production rules are not limited to this form, as they can also have rules of the form A -> BC. Therefore, CNF is not equivalent to regular grammar.
2. Context-Sensitive Grammar (Option B): Context-sensitive grammars have production rules of the form αAβ -> αγβ, where A is a non-terminal, α and β are strings of terminals and non-terminals, and γ is a string of terminals and non-terminals that is not empty. CNF does not fit this form because it restricts the production rules to either A -> BC or A -> a. Therefore, CNF is not equivalent to context-sensitive grammar.
3. Context-Free Grammar (Option C): Context-free grammars have production rules of the form A -> α, where A is a non-terminal, and α is a string of terminals and non-terminals. CNF is a specific form of context-free grammar that satisfies the properties mentioned earlier. Therefore, every grammar in Chomsky Normal Form is a context-free grammar.
In summary, Chomsky Normal Form is a specific form of context-free grammar. It is not equivalent to regular grammar or context-sensitive grammar. Therefore, the correct answer to the question is option C) context-free.
Chomsky Normal Form (CNF)
--------------------------
Chomsky Normal Form (CNF) is a type of context-free grammar (CFG) that has the following properties:
1. Every production rule is of the form A -> BC or A -> a, where A, B, and C are non-terminal symbols, and a is a terminal symbol.
2. The start symbol S does not appear on the right-hand side of any production rule, except for the rule S -> ε, where ε represents the empty string.
In CNF, each production rule either produces two non-terminal symbols or a non-terminal symbol and a terminal symbol. This form simplifies the derivation process and allows for more efficient parsing algorithms.
Explanation of the Answer
--------------------------
The correct answer to the question is "C) context-free." This means that every grammar in Chomsky Normal Form is a context-free grammar (CFG). Here's why:
1. Regular Grammar (Option A): Regular grammars have production rules of the form A -> aB or A -> a, where A and B are non-terminals, and a is a terminal symbol. In CNF, the production rules are not limited to this form, as they can also have rules of the form A -> BC. Therefore, CNF is not equivalent to regular grammar.
2. Context-Sensitive Grammar (Option B): Context-sensitive grammars have production rules of the form αAβ -> αγβ, where A is a non-terminal, α and β are strings of terminals and non-terminals, and γ is a string of terminals and non-terminals that is not empty. CNF does not fit this form because it restricts the production rules to either A -> BC or A -> a. Therefore, CNF is not equivalent to context-sensitive grammar.
3. Context-Free Grammar (Option C): Context-free grammars have production rules of the form A -> α, where A is a non-terminal, and α is a string of terminals and non-terminals. CNF is a specific form of context-free grammar that satisfies the properties mentioned earlier. Therefore, every grammar in Chomsky Normal Form is a context-free grammar.
In summary, Chomsky Normal Form is a specific form of context-free grammar. It is not equivalent to regular grammar or context-sensitive grammar. Therefore, the correct answer to the question is option C) context-free.
Chapter doubts & questions for Theory of Computation - Question Bank for GATE Computer Science Engineering 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Theory of Computation - Question Bank for GATE Computer Science Engineering in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Question Bank for GATE Computer Science Engineering
63 videos|8 docs|165 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup