GATE Exam > GATE Questions > he diagnoalization language, Ld is aa)Recursi...
Start Learning for Free
he diagnoalization language, Ld is a
- a)Recursive language.
- b)Recursive enumerable but not recursive
- c)Non-recurisvily - enumerable (non-RE) language
- d)Both (b) and (c)
Correct answer is option 'B'. Can you explain this answer?
Verified Answer
he diagnoalization language, Ld is aa)Recursive language.b)Recursive e...
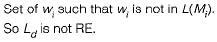
Most Upvoted Answer
he diagnoalization language, Ld is aa)Recursive language.b)Recursive e...
The diagonalization language, Ld, is a language that cannot be enumerated by any Turing machine. In other words, there is no Turing machine that can generate a list of all the strings in Ld.
To understand why Ld is recursively enumerable but not recursive, let's break down the definitions of these terms:
1. Recursive language:
- A language is recursive if there exists a Turing machine that can halt and accept or reject any given input string.
- This means that for any input string, the Turing machine will always reach a final state and provide a definite answer (accept or reject).
2. Recursive enumerable language:
- A language is recursively enumerable if there exists a Turing machine that can enumerate (list) all the strings in the language.
- This means that for any string in the language, the Turing machine will eventually generate it.
- However, the Turing machine may not halt or generate any output for strings that are not in the language.
Now, let's analyze Ld:
- Ld is the language that contains all the binary strings that do not belong to themselves. In other words, for any string x, x is in Ld if and only if x is not in the language described by the xth Turing machine.
- Assume that there exists a Turing machine TMd that can enumerate all the strings in Ld. This means that TMd can generate a list of all the binary strings that do not belong to themselves.
- Now, let's construct a contradiction by considering a new string d, which is the description of a Turing machine that behaves differently than all the Turing machines in the list generated by TMd.
- Since d is different from every Turing machine in the list, it must either belong to Ld or not. However, both possibilities lead to a contradiction:
1. If d is in Ld, it means that d does not belong to itself. But since d is different from all the machines in the list, it must belong to itself. This is a contradiction.
2. If d is not in Ld, it means that d belongs to itself. But again, since d is different from all the machines in the list, it must not belong to itself. This is also a contradiction.
The contradiction arises from assuming the existence of TMd, which means that no Turing machine can enumerate all the strings in Ld. Therefore, Ld is recursively enumerable but not recursive.
To understand why Ld is recursively enumerable but not recursive, let's break down the definitions of these terms:
1. Recursive language:
- A language is recursive if there exists a Turing machine that can halt and accept or reject any given input string.
- This means that for any input string, the Turing machine will always reach a final state and provide a definite answer (accept or reject).
2. Recursive enumerable language:
- A language is recursively enumerable if there exists a Turing machine that can enumerate (list) all the strings in the language.
- This means that for any string in the language, the Turing machine will eventually generate it.
- However, the Turing machine may not halt or generate any output for strings that are not in the language.
Now, let's analyze Ld:
- Ld is the language that contains all the binary strings that do not belong to themselves. In other words, for any string x, x is in Ld if and only if x is not in the language described by the xth Turing machine.
- Assume that there exists a Turing machine TMd that can enumerate all the strings in Ld. This means that TMd can generate a list of all the binary strings that do not belong to themselves.
- Now, let's construct a contradiction by considering a new string d, which is the description of a Turing machine that behaves differently than all the Turing machines in the list generated by TMd.
- Since d is different from every Turing machine in the list, it must either belong to Ld or not. However, both possibilities lead to a contradiction:
1. If d is in Ld, it means that d does not belong to itself. But since d is different from all the machines in the list, it must belong to itself. This is a contradiction.
2. If d is not in Ld, it means that d belongs to itself. But again, since d is different from all the machines in the list, it must not belong to itself. This is also a contradiction.
The contradiction arises from assuming the existence of TMd, which means that no Turing machine can enumerate all the strings in Ld. Therefore, Ld is recursively enumerable but not recursive.

|
Explore Courses for GATE exam
|

|
Question Description
he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer?.
he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer?.
Solutions for he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer?, a detailed solution for he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice he diagnoalization language, Ld is aa)Recursive language.b)Recursive enumerable but not recursivec)Non-recurisvily - enumerable (non-RE) languaged)Both (b) and (c)Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























