All Exams >
Electronics and Communication Engineering (ECE) >
Communication System >
All Questions
All questions of Information Theory & Coding for Electronics and Communication Engineering (ECE) Exam
The maximum rate at which nearly error-free data can be theoretically transmitted over a communication channel is defined as- a)Modulation
- b)Signal to Noise Ratio
- c)Frequency Bandwidth
- d)Channel Capacity
Correct answer is option 'D'. Can you explain this answer?
The maximum rate at which nearly error-free data can be theoretically transmitted over a communication channel is defined as
a)
Modulation
b)
Signal to Noise Ratio
c)
Frequency Bandwidth
d)
Channel Capacity

|
Imtiaz Ahmad answered |
- Channel capacity is the maximum rate at which the data can be transmitted through a channel without errors.
- The capacity of a channel can be increased by increasing channel bandwidth as well as by increasing signal to noise ratio.
- Channel capacity (C) is given as,
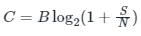
Where,
B: Bandwidth
S/N: Signal to noise ratio
Entropy:
The entropy of a probability distribution is the average or the amount of information when drawing from a probability distribution.
It is calculated as:
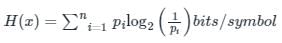
pi is the probability of the occurrence of a symbol.
B: Bandwidth
S/N: Signal to noise ratio
Entropy:
The entropy of a probability distribution is the average or the amount of information when drawing from a probability distribution.
It is calculated as:
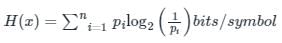
pi is the probability of the occurrence of a symbol.
The Shannon’s Theorem sets limit on the- a)Highest frequency that may be sent over channel
- b)Maximum capacity of a channel with a given noise level
- c)Maximum number coding levels in a channel
- d)Maximum number of quantizing levels in a channel
Correct answer is option 'B'. Can you explain this answer?
The Shannon’s Theorem sets limit on the
a)
Highest frequency that may be sent over channel
b)
Maximum capacity of a channel with a given noise level
c)
Maximum number coding levels in a channel
d)
Maximum number of quantizing levels in a channel

|
Imtiaz Ahmad answered |
Shannon–Hartley theorem:
It states the channel capacity C, i.e. the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
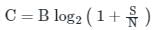
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
∴ It is a measure of capacity on a channel. And it is impossible to transmit information at a faster rate without error.
So that Shannon’s Theorem sets limit on the maximum capacity of a channel with a given noise level.
The Shannon–Hartley theorem establishes that the channel capacity for a finite-bandwidth continuous-time channel is subject to Gaussian noise.
It connects Hartley's result with Shannon's channel capacity theorem in a form that is equivalent to specifying the M in Hartley's line rate formula in terms of a signal-to-noise ratio, but achieving reliability through error-correction coding rather than through reliably distinguishable pulse levels.
Bandwidth and noise affect the rate at which information can be transmitted over an analog channel.
Bandwidth limitations alone do not impose a cap on the maximum information rate because it is still possible for the signal to take on an indefinitely large number of different voltage levels on each symbol pulse, with each slightly different level being assigned a different meaning or bit sequence.
Taking into account both noise and bandwidth limitations, however, there is a limit to the amount of information that can be transferred by a signal of a bounded power, even when sophisticated multi-level encoding techniques are used.
In the channel considered by the Shannon–Hartley theorem, noise and signal are combined by addition. That is, the receiver measures a signal that is equal to the sum of the signal encoding the desired information and a continuous random variable that represents the noise.
It states the channel capacity C, i.e. the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
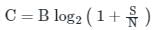
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
∴ It is a measure of capacity on a channel. And it is impossible to transmit information at a faster rate without error.
So that Shannon’s Theorem sets limit on the maximum capacity of a channel with a given noise level.
The Shannon–Hartley theorem establishes that the channel capacity for a finite-bandwidth continuous-time channel is subject to Gaussian noise.
It connects Hartley's result with Shannon's channel capacity theorem in a form that is equivalent to specifying the M in Hartley's line rate formula in terms of a signal-to-noise ratio, but achieving reliability through error-correction coding rather than through reliably distinguishable pulse levels.
Bandwidth and noise affect the rate at which information can be transmitted over an analog channel.
Bandwidth limitations alone do not impose a cap on the maximum information rate because it is still possible for the signal to take on an indefinitely large number of different voltage levels on each symbol pulse, with each slightly different level being assigned a different meaning or bit sequence.
Taking into account both noise and bandwidth limitations, however, there is a limit to the amount of information that can be transferred by a signal of a bounded power, even when sophisticated multi-level encoding techniques are used.
In the channel considered by the Shannon–Hartley theorem, noise and signal are combined by addition. That is, the receiver measures a signal that is equal to the sum of the signal encoding the desired information and a continuous random variable that represents the noise.
A source generates 4 messages. The entropy of the source will be maximum when- a)all probabilities are equal
- b)one of the probabilities equal to 1 and two others are zero
- c)the probabilities are 1/2, 1/4 and 1/2
- d)the two of the probabilities are 1/2 each and other zero
Correct answer is option 'A'. Can you explain this answer?
A source generates 4 messages. The entropy of the source will be maximum when
a)
all probabilities are equal
b)
one of the probabilities equal to 1 and two others are zero
c)
the probabilities are 1/2, 1/4 and 1/2
d)
the two of the probabilities are 1/2 each and other zero
|
|
Ravi Singh answered |
Answer :
- a)all probabilities are equal
The entropy of the source will be maximum when. all probabilities are equal.
one of the probabilities equal to 1 and two others are zero.
Assertion (A): The Shannon-Hartley law shows that we can exchange increased bandwidth for decreased signal power for a system with given capacity C.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.- a)Both A and R are true and R is the correct explanation of A.
- b)Both A and R are true but R is not the correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Assertion (A): The Shannon-Hartley law shows that we can exchange increased bandwidth for decreased signal power for a system with given capacity C.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
Reason (R): The bandwidth and the signal power place a restriction upon the rate of information that can be transmitted by a channel.
a)
Both A and R are true and R is the correct explanation of A.
b)
Both A and R are true but R is not the correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.

|
Sanchita Pillai answered |
According to Shannon-Hartley faw, the channel capacity is expressed as

Thus, if signal power is more, bandwidth will be less and vice-versa. Thus, assertion is a true statement. Reason is also a true statement because the rate of information that can be transmitted depends on bandwidth and signal to noise power. Thus, both assertion and reason are true but reason is not the correct explanation of assertion.
A 1200 band data stream is to be sent over a non-redundant frequency hopping system, The maximum bandwidth for the spread spectrum signal is 10 MHz. if no overlap occurs, the number of channels are equal to- a)2175
- b)3125
- c)4167
- d)5286
Correct answer is option 'C'. Can you explain this answer?
A 1200 band data stream is to be sent over a non-redundant frequency hopping system, The maximum bandwidth for the spread spectrum signal is 10 MHz. if no overlap occurs, the number of channels are equal to
a)
2175
b)
3125
c)
4167
d)
5286

|
Subhankar Ghoshal answered |
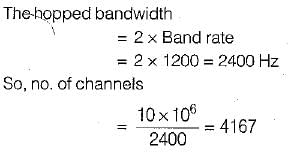
Let (X1, X2) be independent random varibales. X1 has mean 0 and variance 1, while X2 has mean 1 and variance 4. The mutual information I(X1 ; X2) between X1 and X2 in bits is_______.Correct answer is '0'. Can you explain this answer?
Let (X1, X2) be independent random varibales. X1 has mean 0 and variance 1, while X2 has mean 1 and variance 4. The mutual information I(X1 ; X2) between X1 and X2 in bits is_______.
|
|
Kunal Yadav answered |
Understanding Mutual Information
Mutual information quantifies the amount of information obtained about one random variable through another. It is defined mathematically as:
- I(X1; X2) = H(X1) + H(X2) - H(X1, X2)
Where H denotes entropy.
Independence of Random Variables
In the given scenario, X1 and X2 are independent random variables. This independence implies:
- The occurrence of X1 provides no information about X2 and vice versa.
Implications of Independence
For independent random variables:
- I(X1; X2) = 0
This is because when two variables are independent, their joint entropy equals the sum of their individual entropies:
- H(X1, X2) = H(X1) + H(X2)
As a result, the mutual information, which measures shared information, becomes zero.
Specifics of X1 and X2
- X1 has a mean of 0 and variance of 1.
- X2 has a mean of 1 and variance of 4.
These parameters do not affect the independence property. Hence, while their distributions differ, they do not share any information.
Conclusion
Given that X1 and X2 are independent, the mutual information I(X1; X2) is:
- 0 bits
This reflects the absence of any predictive relationship between the two variables.
Mutual information quantifies the amount of information obtained about one random variable through another. It is defined mathematically as:
- I(X1; X2) = H(X1) + H(X2) - H(X1, X2)
Where H denotes entropy.
Independence of Random Variables
In the given scenario, X1 and X2 are independent random variables. This independence implies:
- The occurrence of X1 provides no information about X2 and vice versa.
Implications of Independence
For independent random variables:
- I(X1; X2) = 0
This is because when two variables are independent, their joint entropy equals the sum of their individual entropies:
- H(X1, X2) = H(X1) + H(X2)
As a result, the mutual information, which measures shared information, becomes zero.
Specifics of X1 and X2
- X1 has a mean of 0 and variance of 1.
- X2 has a mean of 1 and variance of 4.
These parameters do not affect the independence property. Hence, while their distributions differ, they do not share any information.
Conclusion
Given that X1 and X2 are independent, the mutual information I(X1; X2) is:
- 0 bits
This reflects the absence of any predictive relationship between the two variables.
Consider the binary Hamming code of block length 31 and rate equal to (26/31). Its minimum distance is
- a)3
- b)5
- c)26
- d)31
Correct answer is option 'A'. Can you explain this answer?
Consider the binary Hamming code of block length 31 and rate equal to (26/31). Its minimum distance is
a)
3
b)
5
c)
26
d)
31

|
Partho Singh answered |
Minimum distance in hamming code = 3.
The minimum distance of a Hamming code is always 3. This property allows Hamming codes to detect up to two-bit errors and correct single-bit errors within a block of data. The minimum distance is not directly related to the block length or rate but is a characteristic of the Hamming code's design.
The minimum distance of a Hamming code is always 3. This property allows Hamming codes to detect up to two-bit errors and correct single-bit errors within a block of data. The minimum distance is not directly related to the block length or rate but is a characteristic of the Hamming code's design.
During transmission over a communication channel bit errors occurs independently with probability 1/2 . If a block of 3 bits are transmitted the probability of at least one bit error is equal to- a)1/2
- b)3/2
- c)7/8
- d)5/8
Correct answer is option 'A'. Can you explain this answer?
During transmission over a communication channel bit errors occurs independently with probability 1/2 . If a block of 3 bits are transmitted the probability of at least one bit error is equal to
a)
1/2
b)
3/2
c)
7/8
d)
5/8

|
Mira Sharma answered |
(1 - p)n + np{ 1 - p)n-1 = Required probability
(Here, n = no. of bits and p = probability) ∴ Required probability
(Here, n = no. of bits and p = probability) ∴ Required probability
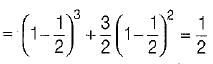
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9) W/Hz?- a)17.4 Mbit/s
- b)12.28 Mbit/s
- c)26.56 Mbit/s
- d)6.64 Mbit/s
Correct answer is option 'B'. Can you explain this answer?
What is the capacity of an additive white Gaussian noise channel with bandwidth of 1 MHz, power of 10W and noise power spectral density of No/2 = 10(−9) W/Hz?
a)
17.4 Mbit/s
b)
12.28 Mbit/s
c)
26.56 Mbit/s
d)
6.64 Mbit/s

|
Starcoders answered |
Additive white Gaussian noise (AWGN) is a basic noise model used in information theory to mimic the effect of many random processes that occur in nature.
The modifiers denote specific characteristics: Additive because it is added to any noise that might be intrinsic to the information system.
The capacity of an additive white Gaussian noise channel by Shanon's formula:
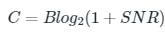
Where B refers to the bandwidth of the channel
SNR means Signal to Noise Ratio : can be defined as the ratio of relevant to irrelevant information in an interface or communication channel.
SNR now can be calculated as,
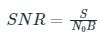
In the above problem, S is the signal power which is equivalent to 10 W.
Bandwidth = 1 MHz
Noise power spectral density of No/2 = 10(−9) W/Hz
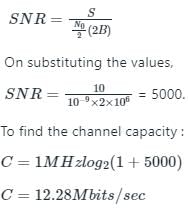
The modifiers denote specific characteristics: Additive because it is added to any noise that might be intrinsic to the information system.
The capacity of an additive white Gaussian noise channel by Shanon's formula:
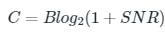
Where B refers to the bandwidth of the channel
SNR means Signal to Noise Ratio : can be defined as the ratio of relevant to irrelevant information in an interface or communication channel.
SNR now can be calculated as,
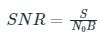
In the above problem, S is the signal power which is equivalent to 10 W.
Bandwidth = 1 MHz
Noise power spectral density of No/2 = 10(−9) W/Hz
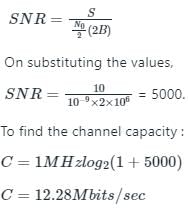
The information capacity (bits/sec) of a channel with bandwidth C and transmission time T is given by - a)C α ω T
- b)C = ω/T
- c)C = T/ω
- d)C = ω2T
Correct answer is option 'D'. Can you explain this answer?
The information capacity (bits/sec) of a channel with bandwidth C and transmission time T is given by
a)
C α ω T
b)
C = ω/T
c)
C = T/ω
d)
C = ω2T

|
Starcoders answered |
Shannon–Hartley theorem:
It states the channel capacity C, i.e. the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
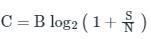
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
It states the channel capacity C, i.e. the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
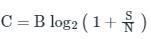
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
An Ideal power limited communication channel with additive white Gaussian noise is having 4 kHz band width and Signal to Noise ratio of 255. The channel capacity is:- a)8 kilo bits / sec
- b)9.63 kilo bits / sec
- c)16 kilo bits / sec
- d)32 kilo bits / sec
Correct answer is option 'D'. Can you explain this answer?
An Ideal power limited communication channel with additive white Gaussian noise is having 4 kHz band width and Signal to Noise ratio of 255. The channel capacity is:
a)
8 kilo bits / sec
b)
9.63 kilo bits / sec
c)
16 kilo bits / sec
d)
32 kilo bits / sec

|
Imtiaz Ahmad answered |
Shannon’s channel capacity is the maximum bits that can be transferred error-free. Mathematically, this is defined as:
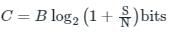
B = Bandwidth of the channel
S/N =Signal to noise ratio
Note: In the expression of channel capacity, S/N is not in dB.
Calculation:
Given B = 4 kHz and SNR = 255
Channel capacity will be:
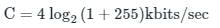
C = 32 kbits/sec
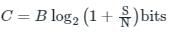
B = Bandwidth of the channel
S/N =Signal to noise ratio
Note: In the expression of channel capacity, S/N is not in dB.
Calculation:
Given B = 4 kHz and SNR = 255
Channel capacity will be:
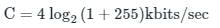
C = 32 kbits/sec
Two binary channels have been connected in a cascade as shown in the figure.
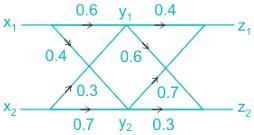
It is given that P(x1) = 0.7 and P(x2) = 0.3, then choose correct option from below.
- a)P(z1) =0.547
- b)P(z2) =0.453
- c)P(x2/y1) =0.376
- d)P(x2/y1) =0.176
Correct answer is option 'D'. Can you explain this answer?
Two binary channels have been connected in a cascade as shown in the figure.

It is given that P(x1) = 0.7 and P(x2) = 0.3, then choose correct option from below.

It is given that P(x1) = 0.7 and P(x2) = 0.3, then choose correct option from below.
a)
P(z1) =0.547
b)
P(z2) =0.453
c)
P(x2/y1) =0.376
d)
P(x2/y1) =0.176

|
Imtiaz Ahmad answered |
For a binary channel as shown below
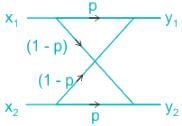
P(yn) = P(xm)P(yn/xm) , n = 1,2 and m = 1,2
Where,
P(yn) → Probability of receiving output yn
P(xm) → Probability of the transmitting signal
P(yn/xm) → Probability of the received output provided x was transmitted
P(xm/yn) = [P(yn/xm)× P(xm)]/P(yn)
Where;
P(xm/yn) → Probability of xm transmitted given that yn was received
Calculation of P(z1);

The marked line shows the path from x1 to z1 (abc and aec) and x2 to z1 (dec and dbc)
Following these paths, we can calculate P(z1)
P(z1) = [P(x1) {(0.6× 0.4) or(0.4 × 0.7}] or [P(x2){(0.3 × 0.4) or (0.7 × 0.7)}]
⇒ P(z1) = [0.7 {(0.6× 0.4) + (0.4 × 0.7}] + [0.3{(0.3 × 0.4) + (0.7 × 0.7)}]
∴ P(z1) = 0.547
Similarly, P(z2) can be calculated;
P(z2) = [P(x1) {(0.6× 0.6) +(0.4 × 0.3}] + [P(x2){(0.3 × 0.6) + (0.7 × 0.3)}] = 0.453
Calculation of P(x2/y1):
P(y1) = (0.7 × 0.6) + (0.3 × 0.3) = 0.51


P(yn) = P(xm)P(yn/xm) , n = 1,2 and m = 1,2
Where,
P(yn) → Probability of receiving output yn
P(xm) → Probability of the transmitting signal
P(yn/xm) → Probability of the received output provided x was transmitted
P(xm/yn) = [P(yn/xm)× P(xm)]/P(yn)
Where;
P(xm/yn) → Probability of xm transmitted given that yn was received
Calculation of P(z1);

The marked line shows the path from x1 to z1 (abc and aec) and x2 to z1 (dec and dbc)
Following these paths, we can calculate P(z1)
P(z1) = [P(x1) {(0.6× 0.4) or(0.4 × 0.7}] or [P(x2){(0.3 × 0.4) or (0.7 × 0.7)}]
⇒ P(z1) = [0.7 {(0.6× 0.4) + (0.4 × 0.7}] + [0.3{(0.3 × 0.4) + (0.7 × 0.7)}]
∴ P(z1) = 0.547
Similarly, P(z2) can be calculated;
P(z2) = [P(x1) {(0.6× 0.6) +(0.4 × 0.3}] + [P(x2){(0.3 × 0.6) + (0.7 × 0.3)}] = 0.453
Calculation of P(x2/y1):
P(y1) = (0.7 × 0.6) + (0.3 × 0.3) = 0.51

For the channel shown below if the source generates two symbols m0 and m1 with a probability of 0.6 and 0.4 respectively. The probability of error if the receiver uses MAP coding will be_______(correct up to two decimal places)
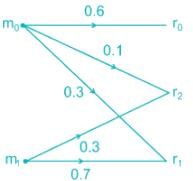 Correct answer is between '0.23,0.25'. Can you explain this answer?
Correct answer is between '0.23,0.25'. Can you explain this answer?
For the channel shown below if the source generates two symbols m0 and m1 with a probability of 0.6 and 0.4 respectively. The probability of error if the receiver uses MAP coding will be_______(correct up to two decimal places)



|
Starcoders answered |
If r0 is received:
P(m0) P(r0/m0) = 0.6 × 0.6 = 0.36
Also,
P(m1) P(r0/m1) = 0.4 × 0 = 0
If r1 is received:
P(m0) P (r1/m0) = (0.6) (0.3)
= 0.18
P(m1) P(r1/m1)
= (0.4) (0.7)
= 0.28
If r2 is received:
P(m0) P(r2/m0)
(0.6) (0.1)
= 0.06
P(m1) P(r2/m1)
= (0.4) (0.3)
= 0.12
Probability of correct detection
Pc = 0.12 + 0.28 + 0.36
= 0.76
Pe = 1 – 0.76
= 0.24
P(m0) P(r0/m0) = 0.6 × 0.6 = 0.36
Also,
P(m1) P(r0/m1) = 0.4 × 0 = 0
If r1 is received:
P(m0) P (r1/m0) = (0.6) (0.3)
= 0.18
P(m1) P(r1/m1)
= (0.4) (0.7)
= 0.28
If r2 is received:
P(m0) P(r2/m0)
(0.6) (0.1)
= 0.06
P(m1) P(r2/m1)
= (0.4) (0.3)
= 0.12
Probability of correct detection
Pc = 0.12 + 0.28 + 0.36
= 0.76
Pe = 1 – 0.76
= 0.24
The Shannon limit for information capacity I is

Where:
N = Noise power (W)
B = Bandwidth (Hz)
S = Signal power (W) - a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
The Shannon limit for information capacity I is

Where:
N = Noise power (W)
B = Bandwidth (Hz)
S = Signal power (W)

Where:
N = Noise power (W)
B = Bandwidth (Hz)
S = Signal power (W)
a)
1
b)
2
c)
3
d)
4

|
Starcoders answered |
Shannon–Hartley theorem:
It states the channel capacity C, meaning the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
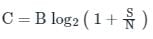
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
∴ It is a measure of capacity on a channel. And it is impossible to transmit information at a faster rate without error.
It states the channel capacity C, meaning the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
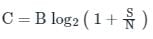
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
∴ It is a measure of capacity on a channel. And it is impossible to transmit information at a faster rate without error.
Consider a Binary - channel
P(x1) = 0.5
P(x2) = 0.5
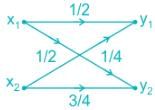
Find the mutual Information in bits/symbolCorrect answer is between '0.04,0.06'. Can you explain this answer?
Consider a Binary - channel
P(x1) = 0.5
P(x2) = 0.5

Find the mutual Information in bits/symbol
P(x1) = 0.5
P(x2) = 0.5

Find the mutual Information in bits/symbol

|
Imtiaz Ahmad answered |
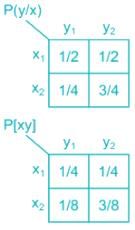
P(y1) = 3/8
P(y2) = 5/8
Mutual Information I(xy)
I(xy) = H(x) - H(x/y)
= H(y) - H(y/x)
H(y) - Σ P(yj) log2 P(yi)
= - [0.375 log2(0.375) + 0.625 log2(0.625)]
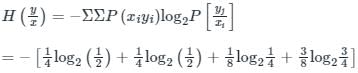
I(xy) = 0.05 bits/symbol
In the communication system, if for a given rate of information transmission requires channel bandwidth, B1 and signal-to-noise ratio SNR1. If the channel bandwidth is doubled for same rate of information then a new signal-to-noise ratio will be- a)SNR1
- b)2SNR1
- c)
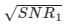
- d)
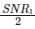
Correct answer is option 'C'. Can you explain this answer?
In the communication system, if for a given rate of information transmission requires channel bandwidth, B1 and signal-to-noise ratio SNR1. If the channel bandwidth is doubled for same rate of information then a new signal-to-noise ratio will be
a)
SNR1
b)
2SNR1
c)
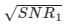
d)
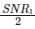

|
Starcoders answered |
Shannon-Hartley Theorem- It tells the maximum rate at which information can be transmitted over a communications channel of a specified bandwidth in the presence of noise.
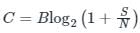
Where C is the channel capacity in bits per second
B is the bandwidth of the channel in hertz
S is the average received signal power over the bandwidth
N is the average noise
S/N is the signal-to-noise ratio (SNR)
For transmitting data without error R ≤ C where R = information rate
Assume information Rate = R
Form Shanon hartley theorem
Rmax = C

When channel Band width (B) = B1
Signal to noise ratio = SNR1

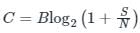
Where C is the channel capacity in bits per second
B is the bandwidth of the channel in hertz
S is the average received signal power over the bandwidth
N is the average noise
S/N is the signal-to-noise ratio (SNR)
For transmitting data without error R ≤ C where R = information rate
Assume information Rate = R
Form Shanon hartley theorem
Rmax = C

When channel Band width (B) = B1
Signal to noise ratio = SNR1

Channel capacity is a measure of -- a)Entropy
- b)Differential entropy
- c)Lower bound on the maximum rate
- d)The maximum rate at which information can be reliably transmitted over a channel
Correct answer is option 'D'. Can you explain this answer?
Channel capacity is a measure of -
a)
Entropy
b)
Differential entropy
c)
Lower bound on the maximum rate
d)
The maximum rate at which information can be reliably transmitted over a channel

|
Imtiaz Ahmad answered |
Channel capacity:
- Channel capacity is the maximum rate at which the data can be transmitted through a channel without errors.
- The capacity of a channel can be increased by increasing channel bandwidth as well as by increasing signal to noise ratio.
- Channel capacity (C) is given as,
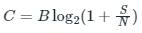
Where,
B: Bandwidth
S/N: Signal to noise ratio
B: Bandwidth
S/N: Signal to noise ratio
Entropy:
The entropy of a probability distribution is the average or the amount of information when drawing from a probability distribution.
It is calculated as:
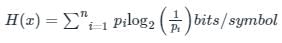
pi is the probability of the occurrence of a symbol.
The entropy of a probability distribution is the average or the amount of information when drawing from a probability distribution.
It is calculated as:
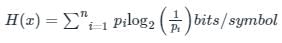
pi is the probability of the occurrence of a symbol.
Read the following expression regarding mutual information I(X;Y). Which of the following expressions is/are correct- a)I(X;Y) = H(X) – H(Y/X)
- b)I(X;Y) = H(X) – H(X/Y)
- c)I(X;Y) = H(X) + H(Y) – H(X,Y)
- d)I(X;Y) = H(X) + H(Y) + H(X,Y)
Correct answer is option 'B,C'. Can you explain this answer?
Read the following expression regarding mutual information I(X;Y). Which of the following expressions is/are correct
a)
I(X;Y) = H(X) – H(Y/X)
b)
I(X;Y) = H(X) – H(X/Y)
c)
I(X;Y) = H(X) + H(Y) – H(X,Y)
d)
I(X;Y) = H(X) + H(Y) + H(X,Y)

|
Starcoders answered |
Mutual Information measures the amount of information that one Random variable contains about another Random variable.
The mutual information between two jointly distributed discrete Random variables X and Y is given by:

In terms of Entropy, this is written as:
I(X ; Y) = H(X) – H(X/Y) ---(1)
(Option (b) is correct)
Also, the conditional entropy states that:
H(X, Y) = H(Y/X) + H(X)
H(X, Y) = H(X/Y) + H(Y)
From above equations we can write:
H(X/Y) = H(X, Y) – H(Y) ---(2)
Using Equations (1) and (2), we can write:
I(X ; Y) = H(X) – [H(X, Y) – H(Y)]
I(X ; Y) = H(X) + H(Y) – H(X, Y) ---(3)
(Option (c) is correct)
The mutual information between two jointly distributed discrete Random variables X and Y is given by:

In terms of Entropy, this is written as:
I(X ; Y) = H(X) – H(X/Y) ---(1)
(Option (b) is correct)
Also, the conditional entropy states that:
H(X, Y) = H(Y/X) + H(X)
H(X, Y) = H(X/Y) + H(Y)
From above equations we can write:
H(X/Y) = H(X, Y) – H(Y) ---(2)
Using Equations (1) and (2), we can write:
I(X ; Y) = H(X) – [H(X, Y) – H(Y)]
I(X ; Y) = H(X) + H(Y) – H(X, Y) ---(3)
(Option (c) is correct)
In data communication using error detection code, as soon as an error is detected, an automatic request for retransmission (ARQ) enables retransmission of data. such binary erasure channel can be modeled as shown:
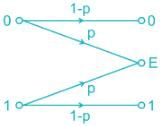
If P = 0.2 and both symbols are generated with equal probability. Then mutual information I(x, y) is _______.Correct answer is '0.8'. Can you explain this answer?
In data communication using error detection code, as soon as an error is detected, an automatic request for retransmission (ARQ) enables retransmission of data. such binary erasure channel can be modeled as shown:

If P = 0.2 and both symbols are generated with equal probability. Then mutual information I(x, y) is _______.

If P = 0.2 and both symbols are generated with equal probability. Then mutual information I(x, y) is _______.

|
Imtiaz Ahmad answered |
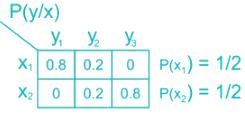
I (xy) = (1 - p) H (x)
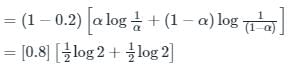
= 0.4 [2 log 2] ( log used is base 2)
⇒ 0.8
A channel has a bandwidth of 8 kHz and signal to noise ratio of 31. For same channel capacity, if the signal to noise ratio is increased to 61, then, the new channel bandwidth would be equal to- a)
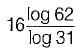
- b)
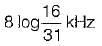
- c)

- d)
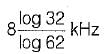
Correct answer is option 'D'. Can you explain this answer?
A channel has a bandwidth of 8 kHz and signal to noise ratio of 31. For same channel capacity, if the signal to noise ratio is increased to 61, then, the new channel bandwidth would be equal to
a)
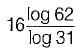
b)
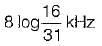
c)

d)
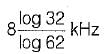

|
Nitya Sharma answered |
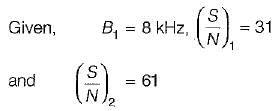
We know that channel capacity is

Since channel capacity remains constant, therefore
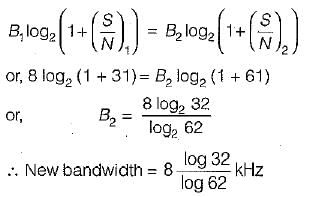
The probabilities of the five possible outcomes of an experiment are given as: If there are 16 outcomes per second then the rate of information would be equal to
If there are 16 outcomes per second then the rate of information would be equal to- a)25 bits/sec
- b)30 bits/sec
- c)35 bits/sec
- d)40 bits/sec
Correct answer is option 'B'. Can you explain this answer?
The probabilities of the five possible outcomes of an experiment are given as:

If there are 16 outcomes per second then the rate of information would be equal to
a)
25 bits/sec
b)
30 bits/sec
c)
35 bits/sec
d)
40 bits/sec

|
Bhaskar Unni answered |
The entropy of the system is
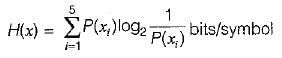
or

Now, rate of outcome r= 16 outcomes/sec (Given)
∴ The rate of information R is
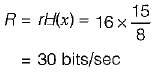
The differential entropy H(x) of the uniformly distributed random variable* with the following probability density function for a = 1 is
- a)-1
- b)0.5
- c)1
- d)0
Correct answer is option 'D'. Can you explain this answer?
The differential entropy H(x) of the uniformly distributed random variable* with the following probability density function for a = 1 is

a)
-1
b)
0.5
c)
1
d)
0

|
Ritika Menon answered |
We know that the differential entropy of x is given by
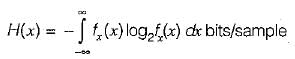
Using the given probability density function, we have:

for
a = 1, H(x) = log2 1 = 0
Match List I with List II:
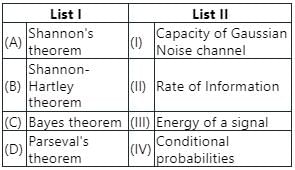
Choose the correct answer from the options given below:- a)(A) - (II), (B) - (I), (C) - (III), (D) - (IV)
- b)(A) - (II), (B) - (I), (C) - (IV), (D) - (III)
- c)(A) - (III), (B) - (II), (C) - (IV), (D) - (I)
- d)(A) - (II), (B) - (III), (C) - (I), (D) - (IV)
Correct answer is option 'B'. Can you explain this answer?
Match List I with List II:

Choose the correct answer from the options given below:

Choose the correct answer from the options given below:
a)
(A) - (II), (B) - (I), (C) - (III), (D) - (IV)
b)
(A) - (II), (B) - (I), (C) - (IV), (D) - (III)
c)
(A) - (III), (B) - (II), (C) - (IV), (D) - (I)
d)
(A) - (II), (B) - (III), (C) - (I), (D) - (IV)

|
Imtiaz Ahmad answered |
It states the channel capacity C, i.e. the theoretical highest upper bound on the information rate of data that can be communicated at an arbitrarily low error rate using an average received signal power S through an analog communication channel that is subject to additive white Gaussian noise (AWGN) of power N.
Mathematically, it is defined as:
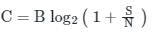
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
Bayes’ theorem
It states that the conditional probability of an event, based on the occurrence of another event, is equal to the likelihood of the second event given the first event multiplied by the probability of the first event.
Parseval's Theorem:
For continuous-time, periodic signal, the energy is given by:
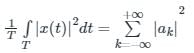
Where ak is the Fourier series coefficient of x(t), and T is the period of the signal.
For average power in one period of the periodic signal x(t), we write:
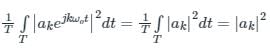
∴ |ak|2 is the average power in the kth harmonic of x(t).
∴ Parseval's relation states that the total average power in a periodic signal equals the sum of the average powers in all of its harmonic components.
Mathematically, it is defined as:
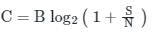
C = Channel capacity
B = Bandwidth of the channel
S = Signal power
N = Noise power
Bayes’ theorem
It states that the conditional probability of an event, based on the occurrence of another event, is equal to the likelihood of the second event given the first event multiplied by the probability of the first event.
Parseval's Theorem:
For continuous-time, periodic signal, the energy is given by:
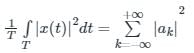
Where ak is the Fourier series coefficient of x(t), and T is the period of the signal.
For average power in one period of the periodic signal x(t), we write:
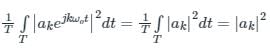
∴ |ak|2 is the average power in the kth harmonic of x(t).
∴ Parseval's relation states that the total average power in a periodic signal equals the sum of the average powers in all of its harmonic components.
Chapter doubts & questions for Information Theory & Coding - Communication System 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Information Theory & Coding - Communication System in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Communication System
13 videos|44 docs|30 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily


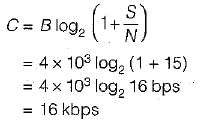
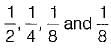 respectively.
respectively.