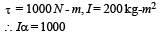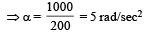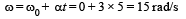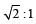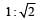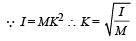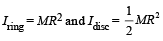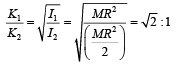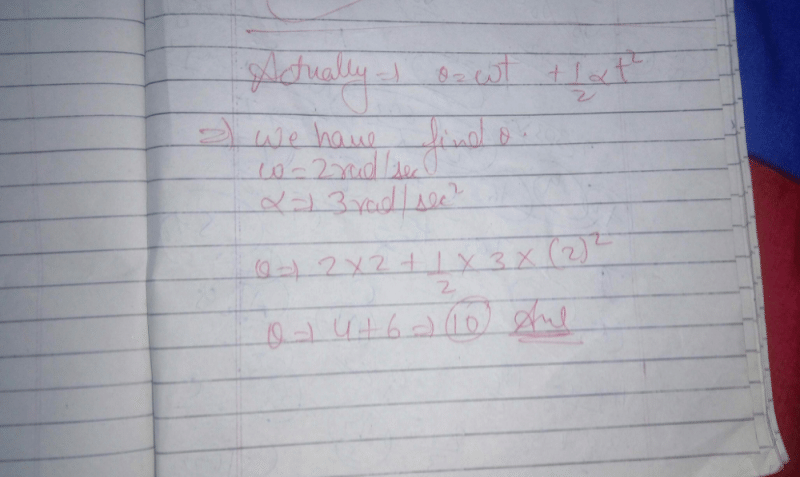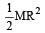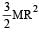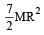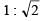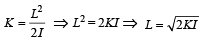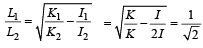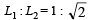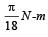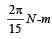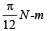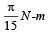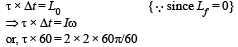All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of System of Particles and Rotational Motion for NEET Exam
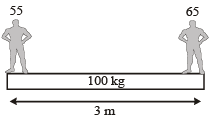
Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat.The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by : [2012]- a)3.0 m
- b)2.3 m
- c)zero
- d)0.75 m
Correct answer is option 'C'. Can you explain this answer?
Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat.The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by : [2012]
a)
3.0 m
b)
2.3 m
c)
zero
d)
0.75 m

|
Ayush Sengupta answered |
There is no external force so centre of mass of the system will not shift
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along : [2012]- a)a line perpendicular to the plane of rotation
- b)the line making an angle of 45° to the plane of rotation
- c)the radius
- d)the tangent to the orbit
Correct answer is option 'A'. Can you explain this answer?
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along : [2012]
a)
a line perpendicular to the plane of rotation
b)
the line making an angle of 45° to the plane of rotation
c)
the radius
d)
the tangent to the orbit
|
|
Cute Princess answered |
A line perpendicular to the plane of rotation.
A small object of uniform density rolls up a curved surface with an initial velocity ‘ν’. It reaches upto a maximum height of 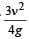 with respect to the initial position. The object is a [NEET 2013]
with respect to the initial position. The object is a [NEET 2013]- a)solid sphere
- b)hollow sphere
- c)disc
- d)ring
Correct answer is option 'C'. Can you explain this answer?
A small object of uniform density rolls up a curved surface with an initial velocity ‘ν’. It reaches upto a maximum height of 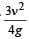 with respect to the initial position. The object is a [NEET 2013]
with respect to the initial position. The object is a [NEET 2013]
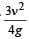 with respect to the initial position. The object is a [NEET 2013]
with respect to the initial position. The object is a [NEET 2013]a)
solid sphere
b)
hollow sphere
c)
disc
d)
ring
|
|
Pallavi Sarkar answered |
Please provide the necessary information for me to assist you.
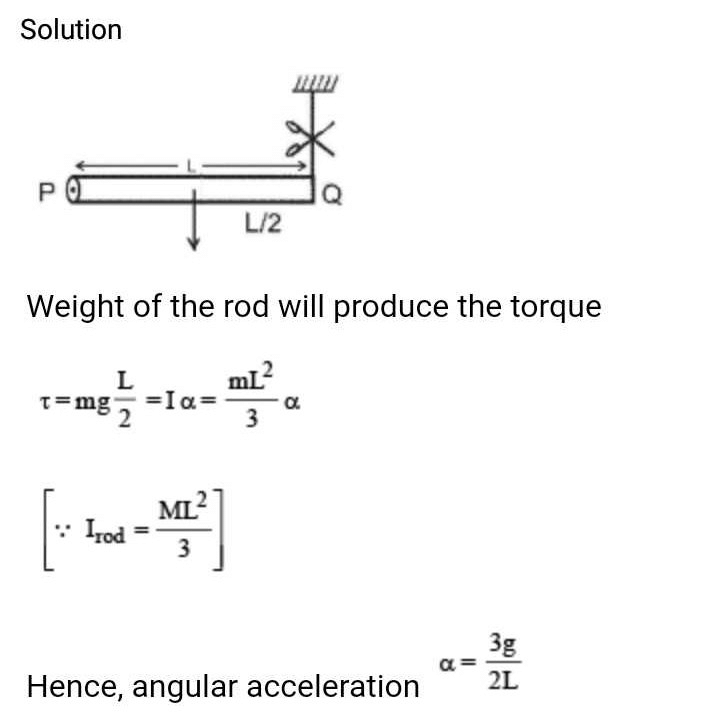
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is [NEET 2013]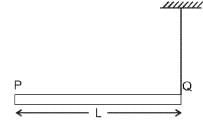
- a)g /L
- b)2g/L
- c)
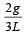
- d)
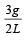
Correct answer is option 'D'. Can you explain this answer?
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is [NEET 2013]

a)
g /L
b)
2g/L
c)
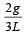
d)
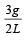
|
|
Wahid Khan answered |
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved ? [2002]- a)Linear momentum
- b)Angular momentum
- c)Kinetic energy
- d)Moment of inertia
Correct answer is option 'B'. Can you explain this answer?
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved ? [2002]
a)
Linear momentum
b)
Angular momentum
c)
Kinetic energy
d)
Moment of inertia

|
Krish Khanna answered |
If external torque is zero, angular momentum remains conserved. [External torque is zero because the weight of child acts downward]
L = Iω = constant
L = Iω = constant
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is[2002]- a)2.5 m
- b)1 m
- c)1.5 m
- d)2 m
Correct answer is option 'D'. Can you explain this answer?
If the linear density (mass per unit length) of a rod of length 3m is proportional to x, where x is the distance from one end of the rod, the distance of the centre of gravity of the rod from this end is[2002]
a)
2.5 m
b)
1 m
c)
1.5 m
d)
2 m
|
|
Sakshi Sharma answered |
Given, linear density of the rod is proportional to x, where x is the distance from one end of the rod.
Let the linear density of the rod at distance x from one end be ρ(x).
We know that the mass of an element of length dx at a distance x from one end is given by dm = ρ(x) dx.
The total mass of the rod is given by integrating the above expression from 0 to 3m:
M = ∫₀³ ρ(x) dx
We also know that the position of the centre of gravity of the rod is given by:
x_bar = (1/M) ∫₀³ x ρ(x) dx
Substituting dm = ρ(x) dx in the above expression, we get:
x_bar = (1/M) ∫₀³ x dm
x_bar = (1/M) ∫₀³ x ρ(x) dx
x_bar = (1/M) ∫₀³ x (kx) dx (since ρ(x) is proportional to x)
x_bar = (k/M) ∫₀³ x² dx
x_bar = (k/M) [x³/3]₀³
x_bar = (k/M) [3³/3]
x_bar = 3k/M
But we know that M = ∫₀³ ρ(x) dx
M = k ∫₀³ x dx
M = k [x²/2]₀³
M = k (9/2)
Therefore, x_bar = 3k/M = 3k/(k(9/2)) = 2/3 * 3 = 2m
Hence, the distance of the centre of gravity of the rod from one end is 2m, which is option D.
Let the linear density of the rod at distance x from one end be ρ(x).
We know that the mass of an element of length dx at a distance x from one end is given by dm = ρ(x) dx.
The total mass of the rod is given by integrating the above expression from 0 to 3m:
M = ∫₀³ ρ(x) dx
We also know that the position of the centre of gravity of the rod is given by:
x_bar = (1/M) ∫₀³ x ρ(x) dx
Substituting dm = ρ(x) dx in the above expression, we get:
x_bar = (1/M) ∫₀³ x dm
x_bar = (1/M) ∫₀³ x ρ(x) dx
x_bar = (1/M) ∫₀³ x (kx) dx (since ρ(x) is proportional to x)
x_bar = (k/M) ∫₀³ x² dx
x_bar = (k/M) [x³/3]₀³
x_bar = (k/M) [3³/3]
x_bar = 3k/M
But we know that M = ∫₀³ ρ(x) dx
M = k ∫₀³ x dx
M = k [x²/2]₀³
M = k (9/2)
Therefore, x_bar = 3k/M = 3k/(k(9/2)) = 2/3 * 3 = 2m
Hence, the distance of the centre of gravity of the rod from one end is 2m, which is option D.
A wheel of radius 1m r olls for war d half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially in contact with the ground is [2002]- a)π
- b)2π
- c)
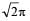
- d)
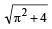
Correct answer is option 'D'. Can you explain this answer?
A wheel of radius 1m r olls for war d half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially in contact with the ground is [2002]
a)
π
b)
2π
c)
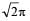
d)
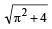

|
Sarthak Saini answered |
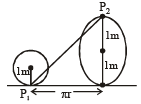
Linear distance moved by wheel in half revolution = πr. Point P1 after half revolution reaches at P2 vertically 2m above the ground.
∴ Displacement P1P2
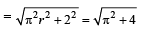 [∵ r = 1m]
[∵ r = 1m]Three masses are placed on the x-axis : 300g at origin, 500g at x = 40cm and 400g at x = 70 cm.The distance of the centre of mass from the origin is : [2012M]- a)40 cm
- b)45 cm
- c)50 cm
- d)30 cm
Correct answer is option 'A'. Can you explain this answer?
Three masses are placed on the x-axis : 300g at origin, 500g at x = 40cm and 400g at x = 70 cm.The distance of the centre of mass from the origin is : [2012M]
a)
40 cm
b)
45 cm
c)
50 cm
d)
30 cm
|
|
Jhanvi Tiwari answered |
Calculation of Centre of Mass:
To find the centre of mass of the system, we can use the formula:
Xcm = (m1x1 + m2x2 + m3x3)/M
where m1, m2, m3 are the masses of the three particles, x1, x2, x3 are their respective distances from the origin, and M = m1 + m2 + m3 is the total mass of the system.
Substituting the given values, we get:
Xcm = (0.3 kg x 0 m + 0.5 kg x 0.4 m + 0.4 kg x 0.7 m)/(0.3 kg + 0.5 kg + 0.4 kg)
Xcm = 0.12 m + 0.2 m + 0.28 m / 1.2 kg
Xcm = 0.6 m
Therefore, the distance of the centre of mass from the origin is 0.6 m or 60 cm.
Answer:
The correct option is (A) 40 cm.
To find the centre of mass of the system, we can use the formula:
Xcm = (m1x1 + m2x2 + m3x3)/M
where m1, m2, m3 are the masses of the three particles, x1, x2, x3 are their respective distances from the origin, and M = m1 + m2 + m3 is the total mass of the system.
Substituting the given values, we get:
Xcm = (0.3 kg x 0 m + 0.5 kg x 0.4 m + 0.4 kg x 0.7 m)/(0.3 kg + 0.5 kg + 0.4 kg)
Xcm = 0.12 m + 0.2 m + 0.28 m / 1.2 kg
Xcm = 0.6 m
Therefore, the distance of the centre of mass from the origin is 0.6 m or 60 cm.
Answer:
The correct option is (A) 40 cm.
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]- a)the surfaces of the discs are made of iron with aluminium inside
- b)the whole of aluminium is kept in the core and the iron at the outer rim of the disc
- c)the whole of the iron is kept in the core and the aluminium at the outer rim of the disc
- d)the whole disc is made with thin alternate sheets of iron and aluminium
Correct answer is option 'B'. Can you explain this answer?
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]
a)
the surfaces of the discs are made of iron with aluminium inside
b)
the whole of aluminium is kept in the core and the iron at the outer rim of the disc
c)
the whole of the iron is kept in the core and the aluminium at the outer rim of the disc
d)
the whole disc is made with thin alternate sheets of iron and aluminium

|
Naveen Menon answered |
Density of iron > density of aluminium moment of inertia 
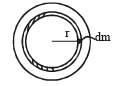
∴ Since, ρiron > ρaluminium
So, whole of aluminium is kept in the core and the iron at the outer rim of the disc.
The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is [2004]- a)1 : √2
- b)1 : 3
- c)2 : 1
- d)√5 : √6
Correct answer is option 'D'. Can you explain this answer?
The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is [2004]
a)
1 : √2
b)
1 : 3
c)
2 : 1
d)
√5 : √6

|
Suvarna Malvekar answered |
Moment of inertia of disc along tangent in plane is 5/4mr^2 and that of ring is 3/2mr^2 then take ratio that is equal to√5/√6.
Two discs are rotating about their axes, normal to the discs and passing through the centres of the discs. Disc D1 has 2 kg mass and 0.2 m radius and initial angular velocity of 50 rad s–1. Disc D2 has 4kg mass, 0.1 m radius and initial angular velocity of 200 rad s–1. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad s–1) of the system is [NEET Kar. 2013]- a)40
- b)60
- c)100
- d)120
Correct answer is option 'C'. Can you explain this answer?
Two discs are rotating about their axes, normal to the discs and passing through the centres of the discs. Disc D1 has 2 kg mass and 0.2 m radius and initial angular velocity of 50 rad s–1. Disc D2 has 4kg mass, 0.1 m radius and initial angular velocity of 200 rad s–1. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad s–1) of the system is [NEET Kar. 2013]
a)
40
b)
60
c)
100
d)
120

|
Abhishek Desai answered |
Given: m1 = 2 kg m2 = 4 kg
r1 = 0.2 m r2 = 0.1 m
w1 = 50 rad s–1 w2 = 200 rad s–1
As, I1W1 = I2W2 = Constant
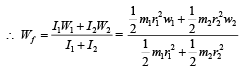
By putting the value of m1, m2, r1, r2 and solving we get = 100 rad s–1
Three particles, each of mass m gram, are situated at the vertices of an equilateral triangle ABC of side l cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm2 units will be [2004]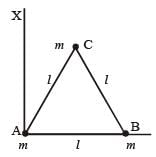
- a)
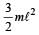
- b)
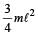
- c)2 mℓ2
- d)
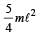
Correct answer is option 'D'. Can you explain this answer?
Three particles, each of mass m gram, are situated at the vertices of an equilateral triangle ABC of side l cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm2 units will be [2004]

a)
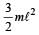
b)
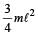
c)
2 mℓ2
d)
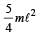
|
|
Gaurav Kumar answered |
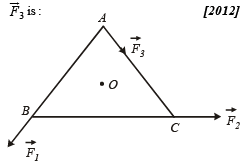
ABC is an equilateral triangle with O as its centre.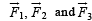 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
- a)F1 + F2
- b)F1 – F2
- c)
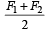
- d) 2(F1 + F2)
Correct answer is option 'A'. Can you explain this answer?
ABC is an equilateral triangle with O as its centre.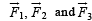 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of

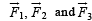 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero the magnitude of
a)
F1 + F2
b)
F1 – F2
c)
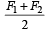
d)
2(F1 + F2)

|
Krish Chakraborty answered |
F1 x + F2 x = F3 x
F3 = F1 + F2
F3 = F1 + F2
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through : [2012M]
- a)B
- b)C
- c)D
- d)A
Correct answer is option 'A'. Can you explain this answer?
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through : [2012M]

a)
B
b)
C
c)
D
d)
A

|
Tejas Chavan answered |
According to parallel axis theorem of the moment of Inertia I = Icm + md2
d is maximum for point B so Imax about B.
A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force [2005]- a)dissipates energy as heat
- b)decreases the rotational motion
- c)decreases the rotational and translational motion
- d)converts translational energy to rotational energy
Correct answer is option 'D'. Can you explain this answer?
A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force [2005]
a)
dissipates energy as heat
b)
decreases the rotational motion
c)
decreases the rotational and translational motion
d)
converts translational energy to rotational energy

|
Pooja Saha answered |
Net work done by frictional force when drum rolls down without slipping is zero.
Wnet = 0
Wnet = 0

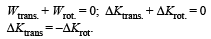
i.e., converts translation energy to rotational energy.
Consider a system of two particles having masses m1 and m2 . If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the centre of mass of particles at the original position? [2004]- a)
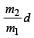
- b)
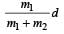
- c)
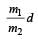
- d)d
Correct answer is option 'C'. Can you explain this answer?
Consider a system of two particles having masses m1 and m2 . If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the centre of mass of particles at the original position? [2004]
a)
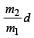
b)
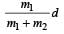
c)
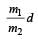
d)
d

|
Kajal Bose answered |

The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t) = 2t3 – 6t2. The torque on the wheel becomes zero at[2011]- a)t = 1s
- b)t = 0.5 s
- c)t = 0.25 s
- d)t = 2s
Correct answer is option 'A'. Can you explain this answer?
The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t) = 2t3 – 6t2. The torque on the wheel becomes zero at[2011]
a)
t = 1s
b)
t = 0.5 s
c)
t = 0.25 s
d)
t = 2s

|
Arnab Iyer answered |
When angular acceleration (α) is zero then torque on the wheel becomes zero. θ(t) = 2t3 – 6t2
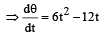
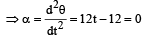
∴ t = 1 sec.
A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass, [2002]- a)h = R
- b)h = 2R
- c)h = 0
- d)The acceleration will be same whatever h may be
Correct answer is option 'D'. Can you explain this answer?
A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass, [2002]
a)
h = R
b)
h = 2R
c)
h = 0
d)
The acceleration will be same whatever h may be

|
Aman Sharma answered |
As friction is absent at the point of contact,
Accelerati on 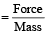
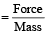
It is independent of h
The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0. Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is [2011]- a)I0 + ML2/2
- b)I0 + ML2/4
- c)I0 + 2ML2
- d)I0 + ML2
Correct answer is option 'B'. Can you explain this answer?
The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is I0. Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is [2011]
a)
I0 + ML2/2
b)
I0 + ML2/4
c)
I0 + 2ML2
d)
I0 + ML2

|
Ruchi Chakraborty answered |
By theorem of parallel axes,
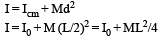
A circular platform is mounted on a frictionless vertical axle. Its radius R = 2 m and its moment of inertia about the axle is 200 kgm2. It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms–1 relative to the ground. Time taken by the man to complete one revolution is :- a)πs
- b)3π / 2 s
- c)2πs
- d)π / 2 s
Correct answer is option 'C'. Can you explain this answer?
A circular platform is mounted on a frictionless vertical axle. Its radius R = 2 m and its moment of inertia about the axle is 200 kgm2. It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms–1 relative to the ground. Time taken by the man to complete one revolution is :
a)
πs
b)
3π / 2 s
c)
2πs
d)
π / 2 s
|
|
Sagnik Jain answered |
By applying the law of conservation of angular momentum,
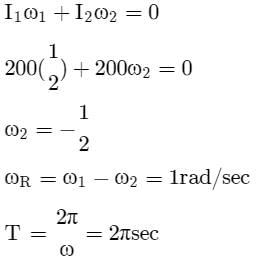
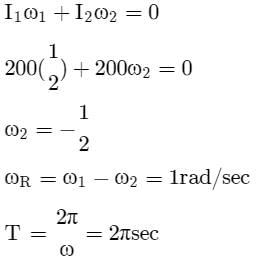
A boy suddenly comes and sits on a circular rotating table. What will remain conserved? [2002]- a)Angular velocity
- b)Angular momentum
- c)Linear momentum
- d)Kinetic energy
Correct answer is option 'B'. Can you explain this answer?
A boy suddenly comes and sits on a circular rotating table. What will remain conserved? [2002]
a)
Angular velocity
b)
Angular momentum
c)
Linear momentum
d)
Kinetic energy

|
Ruchi Chakraborty answered |
As net torque applied is zero. Hence,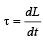
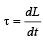
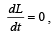 , L = constant.
, L = constant.L (angular momentum) remains conserved.
A particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then
- a)LA = LB [2007]
- b)the relationship between LA and LB depends upon the slope of the line AB
- c)LA < LB
- d)LA > LB
Correct answer is option 'A'. Can you explain this answer?
A particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle with respect to origin O is LA when it is at A and LB when it is at B, then

a)
LA = LB [2007]
b)
the relationship between LA and LB depends upon the slope of the line AB
c)
LA < LB
d)
LA > LB

|
Ishani Nambiar answered |
Angular momentum = Linear momentum × distance of line of action of linear momentum about the origin.
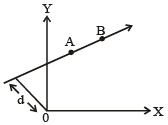
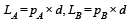
As linear momenta are pA and pB equal, therefore, LA = LB.
A uniform rod AB of length ℓ, and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is 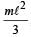 , the initial angular acceleration of the rod will be
, the initial angular acceleration of the rod will be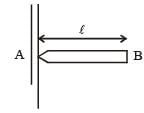
- a)
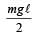
- b)
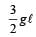
- c)
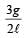
- d)
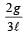
Correct answer is option 'C'. Can you explain this answer?
A uniform rod AB of length ℓ, and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is 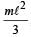 , the initial angular acceleration of the rod will be
, the initial angular acceleration of the rod will be
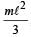 , the initial angular acceleration of the rod will be
, the initial angular acceleration of the rod will be
a)
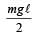
b)
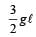
c)
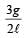
d)
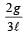
|
|
Ramappa Giddaluru answered |
3
A r ound disc of moment of in ertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combin ation of discs is [2004]- a)
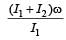
- b)
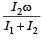
- c)ω
- d)

Correct answer is option 'D'. Can you explain this answer?
A r ound disc of moment of in ertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combin ation of discs is [2004]
a)
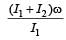
b)
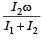
c)
ω
d)


|
Prisha Singh answered |
Angular momentum will be conserved
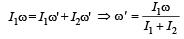
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be [2003]- a)
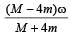
- b)
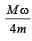
- c)
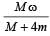
- d)
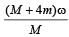
Correct answer is option 'C'. Can you explain this answer?
A thin circular ring of mass M and radius r is rotating about its axis with a constant angular velocity ω. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be [2003]
a)
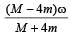
b)
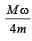
c)
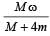
d)
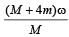

|
Arnab Iyer answered |

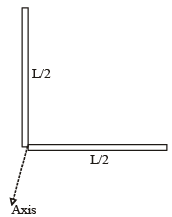
A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90°. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is: [2008]- a)
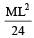
- b)
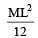
- c)
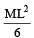
- d)
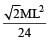
Correct answer is option 'B'. Can you explain this answer?
A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90°. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is: [2008]
a)
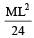
b)
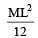
c)
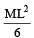
d)
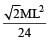

|
Rhea Sarkar answered |
Mass of each part = M/2 Length of each part = L/2
Total M.I. = Sum of M.I.s of both parts
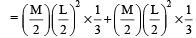
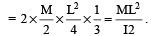
Two bodies of mass 1 kg and 3 kg have position vectors 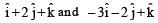 ˆ respectively. The centre of mass of this system has a position vector: [2009]
ˆ respectively. The centre of mass of this system has a position vector: [2009]- a)
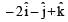
- b)
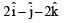
- c)
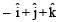
- d)
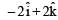
Correct answer is option 'A'. Can you explain this answer?
Two bodies of mass 1 kg and 3 kg have position vectors 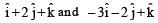 ˆ respectively. The centre of mass of this system has a position vector: [2009]
ˆ respectively. The centre of mass of this system has a position vector: [2009]
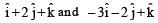 ˆ respectively. The centre of mass of this system has a position vector: [2009]
ˆ respectively. The centre of mass of this system has a position vector: [2009]a)
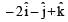
b)
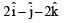
c)
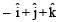
d)
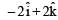

|
Mrinalini Bajaj answered |
The position vector of the centre of mass of two particle system is given by
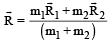
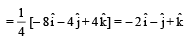
The ratio of the radii or gyration of a circular disc to that of a circular ring, each of same mass and radius, around their respective axes is:- a)
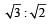
- b)
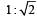 [2008]
[2008] - c)
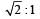
- d)
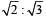
Correct answer is option 'B'. Can you explain this answer?
The ratio of the radii or gyration of a circular disc to that of a circular ring, each of same mass and radius, around their respective axes is:
a)
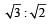
b)
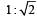 [2008]
[2008]c)
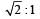
d)
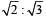

|
Nayanika Dasgupta answered |
The radius of gyration of a circular disc
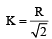
The radius of gyration of a circular ring K' = R (Since both have the same mass and radius)
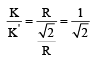
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ? [2003]- a)
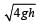
- b)

- c)

- d)
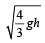
Correct answer is option 'D'. Can you explain this answer?
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ? [2003]
a)
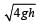
b)

c)

d)
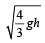

|
Aashna Mukherjee answered |
Applying principle of conservation of total mechanical energy

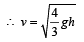
Two particles which are initially at rest, move towards each other under the action of their internal attraction. If their speeds are v and 2v at any instant, then the speed of centre of mass of the system will be: [2010]- a)2v
- b)zero
- c)1.5
- d)v
Correct answer is option 'B'. Can you explain this answer?
Two particles which are initially at rest, move towards each other under the action of their internal attraction. If their speeds are v and 2v at any instant, then the speed of centre of mass of the system will be: [2010]
a)
2v
b)
zero
c)
1.5
d)
v

|
Shivani Tiwari answered |
If n o extern al for ce actson a system of particles, the centre of mass remains at rest.
So, speed of centre of mass is zero.
So, speed of centre of mass is zero.
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is [2006]- a)
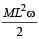
- b)MLω 2
- c)
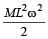
- d)
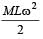
Correct answer is option 'D'. Can you explain this answer?
A tube of length L is filled completely with an incompressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity ω. The force exerted by the liquid at the other end is [2006]
a)
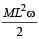
b)
MLω 2
c)
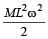
d)
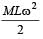
|
|
Yash Modi answered |

A circular disk of moment of inertia It is rotating in a horizontal plane, its symmetry axis, with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disk to friction is:
[2010]- a)
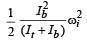
- b)
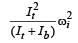
- c)
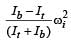
- d)
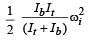
Correct answer is option 'D'. Can you explain this answer?
A circular disk of moment of inertia It is rotating in a horizontal plane, its symmetry axis, with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disk to friction is:
[2010]
[2010]
a)
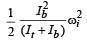
b)
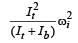
c)
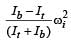
d)
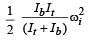
|
|
Yash Modi answered |
Four identical th in rods each of mass M and length l, form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is : [2009]- a)
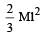
- b)
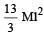
- c)
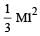
- d)
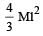
Correct answer is option 'D'. Can you explain this answer?
Four identical th in rods each of mass M and length l, form a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is : [2009]
a)
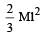
b)
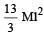
c)
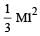
d)
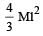

|
Shalini Saha answered |
Moment of in ertia of a thin rod of length l about an axis passing through centre and perpendicular to the rod =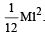
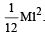
Thus moment of inertia of the frame.
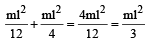
Total M.I. 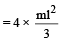
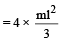
A gramophone recor d is revolving with an angular velocity ω. A coin is placed at a distance r from the centre of the record. The static coefficient of friction is ω. The coin will revolve with the record if: [2010]- a)

- b)
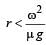
- c)
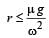
- d)
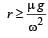
Correct answer is option 'C'. Can you explain this answer?
A gramophone recor d is revolving with an angular velocity ω. A coin is placed at a distance r from the centre of the record. The static coefficient of friction is ω. The coin will revolve with the record if: [2010]
a)

b)
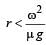
c)
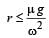
d)
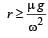

|
Aman Sharma answered |
For the coin to revolve with the record, centrifugal force ≤ frictional force
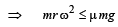
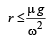
If 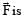 the force acting on a particle having position vector
the force acting on a particle having position vector 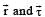 be the tor que of this force about the origin, then: [2009]
be the tor que of this force about the origin, then: [2009]- a)
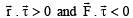
- b)
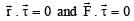
- c)
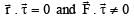
- d)
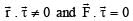
Correct answer is option 'B'. Can you explain this answer?
If 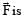 the force acting on a particle having position vector
the force acting on a particle having position vector 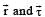 be the tor que of this force about the origin, then: [2009]
be the tor que of this force about the origin, then: [2009]
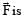 the force acting on a particle having position vector
the force acting on a particle having position vector 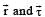 be the tor que of this force about the origin, then: [2009]
be the tor que of this force about the origin, then: [2009]a)
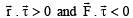
b)
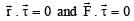
c)
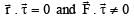
d)
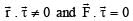

|
Shivani Rane answered |
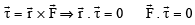
Since, 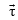 is perpendicular to the plane of
is perpendicular to the plane of 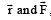 , h ence the dot product of
, h ence the dot product of 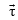 with
with 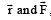 is zero.
is zero.
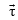 is perpendicular to the plane of
is perpendicular to the plane of 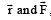 , h ence the dot product of
, h ence the dot product of 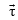 with
with 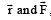 is zero.
is zero.A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K. If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be [2003- a)
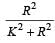
- b)

- c)

- d)
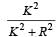
Correct answer is option 'D'. Can you explain this answer?
A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K. If radius of the ball be R, then the fraction of total energy associated with its rotational energy will be [2003
a)
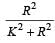
b)

c)

d)
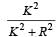

|
Anu Bajaj answered |
Rotational energy 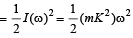
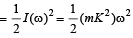
Linear kinetic energy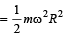
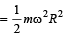
∴ Required fraction
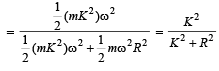
The moment of inertia of a uniform circular disc of radius R and mass M about an axis touching the disc at its diameter and normal to the disc is- a)
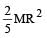
- b)
- c)
- d)MR2
Correct answer is option 'B'. Can you explain this answer?
The moment of inertia of a uniform circular disc of radius R and mass M about an axis touching the disc at its diameter and normal to the disc is
a)
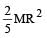
b)
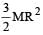
c)
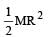
d)
MR2

|
Shanaya Rane answered |
Moment of Inertia of a disc about an axis perpendicular to its face & passing through its centre is
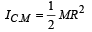
Now, given axis is parallel to the axis given above, so, applying theorem of parallel axis.

A t hin circular ring of mass M an d radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity: [2009]- a)
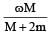
- b)
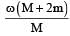
- c)
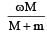
- d)

Correct answer is option 'A'. Can you explain this answer?
A t hin circular ring of mass M an d radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity ω. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity: [2009]
a)
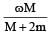
b)
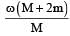
c)
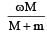
d)


|
Pooja Saha answered |
In absence of exter nal torque, L = Iω = constant
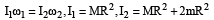
(Moment of inertia of a thin circular ring about an axis vertical to its plane = MR2)
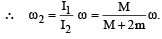
A small mass attached to a string rotates on frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will [2011M]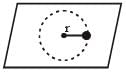
- a)remain constant
- b)increase by a factor of 2
- c)increase by a factor of 4
- d)decrease by a factor of 2
Correct answer is option 'C'. Can you explain this answer?
A small mass attached to a string rotates on frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will [2011M]

a)
remain constant
b)
increase by a factor of 2
c)
increase by a factor of 4
d)
decrease by a factor of 2

|
Ashok Kumar answered |
B
Chapter doubts & questions for System of Particles and Rotational Motion - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of System of Particles and Rotational Motion - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup