NEET Exam > NEET Questions > A composite disc is to be made using equal ma...
Start Learning for Free
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]
- a)the surfaces of the discs are made of iron with aluminium inside
- b)the whole of aluminium is kept in the core and the iron at the outer rim of the disc
- c)the whole of the iron is kept in the core and the aluminium at the outer rim of the disc
- d)the whole disc is made with thin alternate sheets of iron and aluminium
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A composite disc is to be made using equal masses of aluminium and iro...
Density of iron > density of aluminium moment of inertia 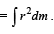
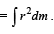
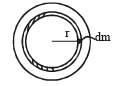
∴ Since, ρiron > ρaluminium
So, whole of aluminium is kept in the core and the iron at the outer rim of the disc.
Most Upvoted Answer
A composite disc is to be made using equal masses of aluminium and iro...
Free Test
| FREE | Start Free Test |
Community Answer
A composite disc is to be made using equal masses of aluminium and iro...
Explanation:
Introduction:
In this question, we are asked to determine the arrangement of aluminium and iron in a composite disc in order to maximize its moment of inertia. Moment of inertia is a measure of an object's resistance to changes in its rotational motion. It depends on the mass distribution of the object.
Analysis:
To analyze the given options and determine the arrangement that maximizes the moment of inertia, we need to understand the concept of moment of inertia and how it is affected by the distribution of mass.
Moment of Inertia:
Moment of inertia, denoted by 'I', is defined as the sum of the products of the masses of individual particles in an object and the square of their respective distances from the axis of rotation. Mathematically, it is represented as:
I = Σmr²
where I = moment of inertia
m = mass of a particle
r = distance of the particle from the axis of rotation
Analysis of Options:
Now, let's analyze each option given and determine which arrangement would maximize the moment of inertia.
Option a) The surfaces of the discs are made of iron with aluminium inside:
In this arrangement, the outer surface is made of iron, and aluminium is placed inside. This arrangement would not maximize the moment of inertia because the majority of the mass (iron) is concentrated at the outer surface, resulting in a smaller moment of inertia compared to other arrangements.
Option b) The whole of aluminium is kept in the core and the iron at the outer rim of the disc:
In this arrangement, all of the aluminium is placed in the core of the disc, while iron is concentrated at the outer rim. This arrangement would maximize the moment of inertia because the majority of the mass (iron) is located farther from the axis of rotation, resulting in a larger moment of inertia compared to other arrangements.
Option c) The whole of the iron is kept in the core and the aluminium at the outer rim of the disc:
In this arrangement, all of the iron is placed in the core of the disc, while aluminium is concentrated at the outer rim. This arrangement would not maximize the moment of inertia because the majority of the mass (aluminium) is located closer to the axis of rotation, resulting in a smaller moment of inertia compared to other arrangements.
Option d) The whole disc is made with thin alternate sheets of iron and aluminium:
In this arrangement, the disc is made by stacking thin alternate sheets of iron and aluminium. This arrangement would not maximize the moment of inertia because the mass distribution is uniform throughout the disc, resulting in a smaller moment of inertia compared to other arrangements.
Conclusion:
Based on the analysis, option b) The whole of aluminium is kept in the core and the iron at the outer rim of the disc would result in the highest moment of inertia. This is because the majority of the mass (iron) is located farther from the axis of rotation, leading to a larger moment of inertia.
Introduction:
In this question, we are asked to determine the arrangement of aluminium and iron in a composite disc in order to maximize its moment of inertia. Moment of inertia is a measure of an object's resistance to changes in its rotational motion. It depends on the mass distribution of the object.
Analysis:
To analyze the given options and determine the arrangement that maximizes the moment of inertia, we need to understand the concept of moment of inertia and how it is affected by the distribution of mass.
Moment of Inertia:
Moment of inertia, denoted by 'I', is defined as the sum of the products of the masses of individual particles in an object and the square of their respective distances from the axis of rotation. Mathematically, it is represented as:
I = Σmr²
where I = moment of inertia
m = mass of a particle
r = distance of the particle from the axis of rotation
Analysis of Options:
Now, let's analyze each option given and determine which arrangement would maximize the moment of inertia.
Option a) The surfaces of the discs are made of iron with aluminium inside:
In this arrangement, the outer surface is made of iron, and aluminium is placed inside. This arrangement would not maximize the moment of inertia because the majority of the mass (iron) is concentrated at the outer surface, resulting in a smaller moment of inertia compared to other arrangements.
Option b) The whole of aluminium is kept in the core and the iron at the outer rim of the disc:
In this arrangement, all of the aluminium is placed in the core of the disc, while iron is concentrated at the outer rim. This arrangement would maximize the moment of inertia because the majority of the mass (iron) is located farther from the axis of rotation, resulting in a larger moment of inertia compared to other arrangements.
Option c) The whole of the iron is kept in the core and the aluminium at the outer rim of the disc:
In this arrangement, all of the iron is placed in the core of the disc, while aluminium is concentrated at the outer rim. This arrangement would not maximize the moment of inertia because the majority of the mass (aluminium) is located closer to the axis of rotation, resulting in a smaller moment of inertia compared to other arrangements.
Option d) The whole disc is made with thin alternate sheets of iron and aluminium:
In this arrangement, the disc is made by stacking thin alternate sheets of iron and aluminium. This arrangement would not maximize the moment of inertia because the mass distribution is uniform throughout the disc, resulting in a smaller moment of inertia compared to other arrangements.
Conclusion:
Based on the analysis, option b) The whole of aluminium is kept in the core and the iron at the outer rim of the disc would result in the highest moment of inertia. This is because the majority of the mass (iron) is located farther from the axis of rotation, leading to a larger moment of inertia.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer?
Question Description
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer?.
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A composite disc is to be made using equal masses of aluminium and iron so that it has as high a moment of inertia as possible. This is possible when [2002]a)the surfaces of the discs are made of iron with aluminium insideb)the whole of aluminium is kept in the core and the iron at the outer rim of the discc)the whole of the iron is kept in the core and the aluminium at the outer rim of the discd)the whole disc is made with thin alternate sheets of iron and aluminiumCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























