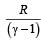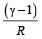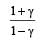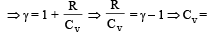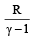All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Thermal Properties of Matter for NEET Exam
Consider a compound slab consisting of two different materials having equal thicknesses and thermal conductivities K and 2K, respectively.
The equivalent thermal conductivity of the slab is [2003]- a)
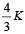
- b)
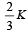
- c)
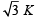
- d)3 K
Correct answer is option 'A'. Can you explain this answer?
Consider a compound slab consisting of two different materials having equal thicknesses and thermal conductivities K and 2K, respectively.
The equivalent thermal conductivity of the slab is [2003]
The equivalent thermal conductivity of the slab is [2003]
a)
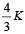
b)
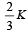
c)
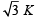
d)
3 K

|
Rajeev Sharma answered |
In series, equivalent thermal conductivity
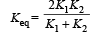

A black body is at 727° C. It emits energy at a rate which is proportional to [2007]- a)(1000)4
- b)(1000)2
- c)727)4
- d)(727)2
Correct answer is option 'A'. Can you explain this answer?
A black body is at 727° C. It emits energy at a rate which is proportional to [2007]
a)
(1000)4
b)
(1000)2
c)
727)4
d)
(727)2

|
Ashwini Khanna answered |
According to Stefan's law, E ∝ T4
∝ (t + 273)4 K [727°C = (727 + 273)K]
∝ (727 + 273)4 K
∝ (1000)4 K
∝ (727 + 273)4 K
∝ (1000)4 K
A body cools from 50.0°C to 48°C in 5s. How long will it take to cool from 40.0°C to 39°C?Assume the temperature of surroundings to be 30.0°C and Newton's law of cooling to be valid.
- a)2.5 sec
- b)10 sec
- c)20 sec
- d)9 sec
Correct answer is option 'B'. Can you explain this answer?
A body cools from 50.0°C to 48°C in 5s. How long will it take to cool from 40.0°C to 39°C?Assume the temperature of surroundings to be 30.0°C and Newton's law of cooling to be valid.
a)
2.5 sec
b)
10 sec
c)
20 sec
d)
9 sec

|
Maheshwar Saini answered |
Rate of cooling ∝ temperature difference between system and surrounding.
As the temperature difference is halved, so the rate of cooling will also be halved
As the temperature difference is halved, so the rate of cooling will also be halved
Radiation from which of the following sources, approximates black body radiation best? [2002]- a)A tungsten lamp
- b)Sodium flame
- c)Hot lamp black
- d)A hole in a cavity, maintained at constant temperature
Correct answer is option 'D'. Can you explain this answer?
Radiation from which of the following sources, approximates black body radiation best? [2002]
a)
A tungsten lamp
b)
Sodium flame
c)
Hot lamp black
d)
A hole in a cavity, maintained at constant temperature
|
|
Zaid Ali answered |
Option D this holed cavity is also called Fery's black body it is made such that when light enter the cavity it suffer multiple reflection inside it and since with every reflection some part is absorbed so almost all the radiant light get absorbed...
A piece of iron is heated in a flame. It first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using [NEET 2013]- a)Wien’s displacement law
- b)Kirchoff’s law
- c)Newton’s law of cooling
- d)Stefan’s law
Correct answer is option 'A'. Can you explain this answer?
A piece of iron is heated in a flame. It first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using [NEET 2013]
a)
Wien’s displacement law
b)
Kirchoff’s law
c)
Newton’s law of cooling
d)
Stefan’s law

|
Srishti Sen answered |
Wein’s displacement law According to this law
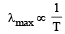
or, λmax × T = constant
So, as the temperature increases λ decreases.
So, as the temperature increases λ decreases.
If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q ? [2012](σ stands for Stefan’S constant)- a)Q/4πR2σ
- b)(Q/4πR2σ)–1/2
- c)(4πR2Q/σ)1/4
- d)(Q/4πR2σ)1/4
Correct answer is option 'D'. Can you explain this answer?
If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q ? [2012]
(σ stands for Stefan’S constant)
a)
Q/4πR2σ
b)
(Q/4πR2σ)–1/2
c)
(4πR2Q/σ)1/4
d)
(Q/4πR2σ)1/4

|
Ashwini Khanna answered |
Stefan’s law for black body radiation Q = σe AT4
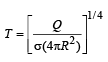
Here e = 1
A = 4πR2
A = 4πR2
An electric kettle takes 4A current at 220 V. How much time will it take to boil 1 kg of water from temperature 20° C? The temperature of boiling water is 100° C. [2008]- a)6.3 min
- b)8.4 min
- c)12.6 min
- d)4.2 min
Correct answer is option 'A'. Can you explain this answer?
An electric kettle takes 4A current at 220 V. How much time will it take to boil 1 kg of water from temperature 20° C? The temperature of boiling water is 100° C. [2008]
a)
6.3 min
b)
8.4 min
c)
12.6 min
d)
4.2 min

|
Ishaan Menon answered |
Heat required to raise the temperature of 1kg water from 20°C to 100°C is given by Q = msΔθ = (1× 4200 × 80) J
Power of kettle (P) = VI = (220 × 4)W
Power of kettle (P) = VI = (220 × 4)W
∴ Time taken =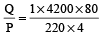
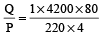
= 381.81 sec = 6.36 min
The density of water at 20°C is 998 kg/m3 and at 40°C 992 kg/m3. The coefficient of volume expansion of water is [NEET Kar. 2013]- a)10–4/°C
- b)3 × 10–4/°C
- c)2 × 10–4/°C
- d)6 × 10–4/°C
Correct answer is option 'B'. Can you explain this answer?
The density of water at 20°C is 998 kg/m3 and at 40°C 992 kg/m3. The coefficient of volume expansion of water is [NEET Kar. 2013]
a)
10–4/°C
b)
3 × 10–4/°C
c)
2 × 10–4/°C
d)
6 × 10–4/°C
|
|
Priya Menon answered |
From question, Δρ = (998 – 992) kg/m3 = 6 kg/m3
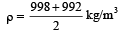 = 995 kg/m3
= 995 kg/m3
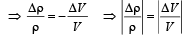
∴ Coefficient of volume expansion of water,
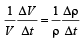
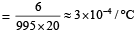
N molecules each of mass m of a gas A and 2N molecules each of mass 2m of gas B are contained in the same vessel which is maintained at temperature T. The mean square velocity of molecules of B type is v2 and the mean square rectangular component of the velocity of A type is denoted by ω2. Then ω2/v2 [1991]- a)2
- b)1
- c)1/3
- d)2/3
Correct answer is option 'D'. Can you explain this answer?
N molecules each of mass m of a gas A and 2N molecules each of mass 2m of gas B are contained in the same vessel which is maintained at temperature T. The mean square velocity of molecules of B type is v2 and the mean square rectangular component of the velocity of A type is denoted by ω2. Then ω2/v2 [1991]
a)
2
b)
1
c)
1/3
d)
2/3

|
Aashna Mukherjee answered |
Mean kinetic energy of the two types of molecules should be equal. The mean square velocity of A type molecules = ω2 + ω2 + ω2 = 3ω2
Therefore, 

This gives ω2 / v2 = 2/3
The presence of gravitational field is required for the heat transfer by [2000]- a)con duction
- b)stirring of liquids
- c)natural convection
- d)radiation
Correct answer is option 'C'. Can you explain this answer?
The presence of gravitational field is required for the heat transfer by [2000]
a)
con duction
b)
stirring of liquids
c)
natural convection
d)
radiation

|
Shruti Chauhan answered |
In convection, the temperature gradient exists in the vertical direction and not in the horizontal direction. So, up and down movement of particles takes place which depends on the weight and gravity.
Two rods of thermal conductivities K1 and K2, cross-sections A1 and A2 and specific heats S1 and S2 are of equal lengths. The temperatures of two ends of each rod are T1 and T2. The rate of flow of heat at the steady state will be equal if [2002]- a)

- b)K1A1 = K2A2
- c)K1S1 = K2S2
- d)A1S1 = A2S2
Correct answer is option 'B'. Can you explain this answer?
Two rods of thermal conductivities K1 and K2, cross-sections A1 and A2 and specific heats S1 and S2 are of equal lengths. The temperatures of two ends of each rod are T1 and T2. The rate of flow of heat at the steady state will be equal if [2002]
a)

b)
K1A1 = K2A2
c)
K1S1 = K2S2
d)
A1S1 = A2S2
|
|
Hansa Sharma answered |
Rate of heat flow for one rod
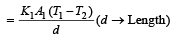
.Rate of heat flow for other rod
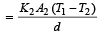
In steady state, 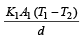
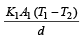
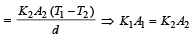
A cylindrical metallic rod in therrnal contact with two reservoirs of heat at its two ends conducts an amount of heat Q in time t. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod, when placed in thermal contact with the two reservoirs in time t? [2010]- a)
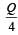
- b)

- c)2Q
- d)
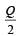
Correct answer is option 'B'. Can you explain this answer?
A cylindrical metallic rod in therrnal contact with two reservoirs of heat at its two ends conducts an amount of heat Q in time t. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod, when placed in thermal contact with the two reservoirs in time t? [2010]
a)
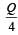
b)

c)
2Q
d)
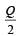
|
|
Yash Modi answered |
If 1 g of steam is mixed with 1 g of ice, then the resultant temperature of the mixture is [1999]- a)270ºC
- b)230ºC
- c)100ºC
- d)50ºC
Correct answer is option 'C'. Can you explain this answer?
If 1 g of steam is mixed with 1 g of ice, then the resultant temperature of the mixture is [1999]
a)
270ºC
b)
230ºC
c)
100ºC
d)
50ºC

|
Pooja Choudhary answered |
Heat required by ice a t 0° C to reach a temperature of 100°C = mL + mcΔθ = 1 × 80 + 1 × 1 × (100 – 0) = 180 cal
Heat available with 1 g steam to condense into 1 g of water at 100°C = 536 cal.
Obviously the whole steam will not be condensed and ice will attain a temperature of 100°C; so the temperature of mixture = 100°C.
Heat available with 1 g steam to condense into 1 g of water at 100°C = 536 cal.
Obviously the whole steam will not be condensed and ice will attain a temperature of 100°C; so the temperature of mixture = 100°C.
The radiant energy from the sun, incident normally at the surface of earth is 20 k cal/m2 min. What would have been the radiant energy, incident normally on the earth, if the sun had a temperature, twice of the present one? [1998]- a)160 k cal/m2 min
- b)40 k cal/m2 min
- c)320k cal/m2 min
- d)80 k cal/m2 min
Correct answer is option 'C'. Can you explain this answer?
The radiant energy from the sun, incident normally at the surface of earth is 20 k cal/m2 min. What would have been the radiant energy, incident normally on the earth, if the sun had a temperature, twice of the present one? [1998]
a)
160 k cal/m2 min
b)
40 k cal/m2 min
c)
320k cal/m2 min
d)
80 k cal/m2 min
|
|
Gargi Yadav answered |
Solution:
To solve this problem, we need to use the Stefan-Boltzmann law, which states that the radiant energy emitted by a black body is proportional to the fourth power of its temperature.
The radiant energy incident normally on the surface of the Earth can be given by the equation:
E = σT^4
Where E is the radiant energy, σ is the Stefan-Boltzmann constant, and T is the temperature of the sun.
We are given that the radiant energy incident normally on the surface of the Earth is 20 k cal/m2 min. Let's assume the temperature of the sun is T1.
So, we have:
20 = σT1^4 .......(1)
We need to find the radiant energy incident normally on the Earth's surface if the sun had a temperature twice of the present one. Let's assume the new temperature of the sun is T2.
So, the new radiant energy can be given by:
E' = σT2^4
We know that T2 = 2T1 (twice the present temperature). Substituting this value into the equation above, we get:
E' = σ(2T1)^4
= σ16T1^4
= 16σT1^4
Now, we need to find the ratio of the new radiant energy (E') to the old radiant energy (E) to determine how much it has increased:
E'/E = (16σT1^4)/(σT1^4)
= 16
Therefore, the new radiant energy is 16 times the old radiant energy.
Given that the old radiant energy is 20 k cal/m2 min, the new radiant energy will be:
E' = 16 * 20 k cal/m2 min
= 320 k cal/m2 min
Hence, the correct answer is option C) 320 k cal/m2 min.
To solve this problem, we need to use the Stefan-Boltzmann law, which states that the radiant energy emitted by a black body is proportional to the fourth power of its temperature.
The radiant energy incident normally on the surface of the Earth can be given by the equation:
E = σT^4
Where E is the radiant energy, σ is the Stefan-Boltzmann constant, and T is the temperature of the sun.
We are given that the radiant energy incident normally on the surface of the Earth is 20 k cal/m2 min. Let's assume the temperature of the sun is T1.
So, we have:
20 = σT1^4 .......(1)
We need to find the radiant energy incident normally on the Earth's surface if the sun had a temperature twice of the present one. Let's assume the new temperature of the sun is T2.
So, the new radiant energy can be given by:
E' = σT2^4
We know that T2 = 2T1 (twice the present temperature). Substituting this value into the equation above, we get:
E' = σ(2T1)^4
= σ16T1^4
= 16σT1^4
Now, we need to find the ratio of the new radiant energy (E') to the old radiant energy (E) to determine how much it has increased:
E'/E = (16σT1^4)/(σT1^4)
= 16
Therefore, the new radiant energy is 16 times the old radiant energy.
Given that the old radiant energy is 20 k cal/m2 min, the new radiant energy will be:
E' = 16 * 20 k cal/m2 min
= 320 k cal/m2 min
Hence, the correct answer is option C) 320 k cal/m2 min.
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]- a)1.24 J/m/s/°C
- b)1.29 J/m/s/°C
- c)2.05 J/m/s/°C
- d)1.02 J/m/s/°C
Correct answer is option 'A'. Can you explain this answer?
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]
a)
1.24 J/m/s/°C
b)
1.29 J/m/s/°C
c)
2.05 J/m/s/°C
d)
1.02 J/m/s/°C

|
Pankaj Banerjee answered |

Rate of heat given by steam = Rate of heat taken by ice where
K = Thermal conductivity of the slab
m = Mass of the ice
L = Latent heat of melting/fusion
A = Area of the slab
K = Thermal conductivity of the slab
m = Mass of the ice
L = Latent heat of melting/fusion
A = Area of the slab

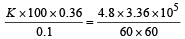
K =1.24 J/m/s/°C
A black body at 1227°C emits radiations with maximum intensity at a wavelength of 5000Å. If the temperature of the body is increased by 1000°C, the maximum intensity will be observed at
- a)5000Å
- b)6000Å
- c)3000Å
- d)4000Å
Correct answer is option 'C'. Can you explain this answer?
A black body at 1227°C emits radiations with maximum intensity at a wavelength of 5000Å. If the temperature of the body is increased by 1000°C, the maximum intensity will be observed at
a)
5000Å
b)
6000Å
c)
3000Å
d)
4000Å

|
Ayush Choudhury answered |
Applying Wein's displacement law, λmT = constant
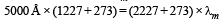
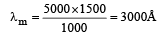
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends.Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2, respectively. If the rate of heat conduction in rod 1 is four times that in rod 2, then [NEET Kar. 2013]- a)K1A1 = K2A2
- b)K1A1 = 4K2A2
- c)K1A1 = 2K2A2
- d)4K1A1 = K2A2
Correct answer is option 'B'. Can you explain this answer?
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends.Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2, respectively. If the rate of heat conduction in rod 1 is four times that in rod 2, then [NEET Kar. 2013]
a)
K1A1 = K2A2
b)
K1A1 = 4K2A2
c)
K1A1 = 2K2A2
d)
4K1A1 = K2A2
|
|
Nishtha Chopra answered |
**Given Information:**
- Two metal rods, 1 and 2, have the same length and the same temperature difference between their ends.
- The thermal conductivities of the rods are represented as K1 and K2.
- The cross-sectional areas of the rods are represented as A1 and A2.
- The rate of heat conduction in rod 1 is four times that in rod 2.
**To Find:**
The relationship between the thermal conductivities and cross-sectional areas of the rods.
**Explanation:**
Let's assume the rate of heat conduction in rod 1 is Q1 and in rod 2 is Q2.
According to Fourier's Law of Heat Conduction, the rate of heat conduction is given by:
Q = (k * A * ΔT) / L,
where Q is the rate of heat conduction, k is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and L is the length of the rod.
**Step 1:**
Using the given information, we can write the equations for the rates of heat conduction in rod 1 and rod 2 as follows:
Q1 = (K1 * A1 * ΔT) / L,
Q2 = (K2 * A2 * ΔT) / L.
**Step 2:**
Given that the rate of heat conduction in rod 1 is four times that in rod 2, we can write the equation:
Q1 = 4 * Q2.
**Step 3:**
Substituting the expressions for Q1 and Q2 from Step 1 into the equation from Step 2, we get:
(K1 * A1 * ΔT) / L = 4 * (K2 * A2 * ΔT) / L.
**Step 4:**
Canceling out the common terms (ΔT and L) from both sides of the equation, we get:
K1 * A1 = 4 * K2 * A2.
**Step 5:**
Rearranging the equation, we obtain:
K1 * A1 = 4 * K2 * A2.
Therefore, the correct answer is option b) K1A1 = 4K2A2, which shows the relationship between the thermal conductivities and cross-sectional areas of the rods.
- Two metal rods, 1 and 2, have the same length and the same temperature difference between their ends.
- The thermal conductivities of the rods are represented as K1 and K2.
- The cross-sectional areas of the rods are represented as A1 and A2.
- The rate of heat conduction in rod 1 is four times that in rod 2.
**To Find:**
The relationship between the thermal conductivities and cross-sectional areas of the rods.
**Explanation:**
Let's assume the rate of heat conduction in rod 1 is Q1 and in rod 2 is Q2.
According to Fourier's Law of Heat Conduction, the rate of heat conduction is given by:
Q = (k * A * ΔT) / L,
where Q is the rate of heat conduction, k is the thermal conductivity, A is the cross-sectional area, ΔT is the temperature difference, and L is the length of the rod.
**Step 1:**
Using the given information, we can write the equations for the rates of heat conduction in rod 1 and rod 2 as follows:
Q1 = (K1 * A1 * ΔT) / L,
Q2 = (K2 * A2 * ΔT) / L.
**Step 2:**
Given that the rate of heat conduction in rod 1 is four times that in rod 2, we can write the equation:
Q1 = 4 * Q2.
**Step 3:**
Substituting the expressions for Q1 and Q2 from Step 1 into the equation from Step 2, we get:
(K1 * A1 * ΔT) / L = 4 * (K2 * A2 * ΔT) / L.
**Step 4:**
Canceling out the common terms (ΔT and L) from both sides of the equation, we get:
K1 * A1 = 4 * K2 * A2.
**Step 5:**
Rearranging the equation, we obtain:
K1 * A1 = 4 * K2 * A2.
Therefore, the correct answer is option b) K1A1 = 4K2A2, which shows the relationship between the thermal conductivities and cross-sectional areas of the rods.
A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°. What is the fall in temperature as registered by the Centigrade thermometer ?- a)80°
- b)60° [1990]
- c)40°
- d)30°
Correct answer is option 'C'. Can you explain this answer?
A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°. What is the fall in temperature as registered by the Centigrade thermometer ?
a)
80°
b)
60° [1990]
c)
40°
d)
30°

|
Pooja Choudhary answered |
Using 

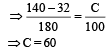
Temperature of boiling water = 100°C
We get, fall in temperature = 100 – 60 = 40°C
We get, fall in temperature = 100 – 60 = 40°C
A cylindrical rod having temperature T1 and T2 at its end. The rate of flow of heat is Q1 cal/sec.If all the linear dimensions are doubled keeping temperature constant, then the rate of flow of heat Q2 will be [2001]- a)4Q1
- b)2Q1
- c)Q1/4
- d)Q1/2
Correct answer is option 'B'. Can you explain this answer?
A cylindrical rod having temperature T1 and T2 at its end. The rate of flow of heat is Q1 cal/sec.If all the linear dimensions are doubled keeping temperature constant, then the rate of flow of heat Q2 will be [2001]
a)
4Q1
b)
2Q1
c)
Q1/4
d)
Q1/2

|
Rhea Sarkar answered |
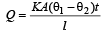
Rate of heat flow
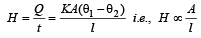
Dimensions of area A = [L2], dimensions of distance l = [L]

Thermal capacity of 40 g of aluminium (s = 0.2 cal /g K) is [1990]- a)168 joule /°C
- b)672 joule/°C
- c)840 joule/°C
- d)33.6 joule/°C
Correct answer is option 'D'. Can you explain this answer?
Thermal capacity of 40 g of aluminium (s = 0.2 cal /g K) is [1990]
a)
168 joule /°C
b)
672 joule/°C
c)
840 joule/°C
d)
33.6 joule/°C

|
Mehul Iyer answered |
Thermal capacity = ms = 40 × 0.2 = 8 cal/°C = 4.2 × 8 J = 33.6 joules/°C
10 gm of ice cubes at 0°C are released in a tumbler (water equivalent 55 g) at 40°C.Assuming that negligible heat is taken from the surroundings, the temperature of water in the tumbler becomes nearly (L = 80 cal/g) [1988]- a)31°C
- b)22°C
- c)19°C
- d)15°C
Correct answer is option 'B'. Can you explain this answer?
10 gm of ice cubes at 0°C are released in a tumbler (water equivalent 55 g) at 40°C.Assuming that negligible heat is taken from the surroundings, the temperature of water in the tumbler becomes nearly (L = 80 cal/g) [1988]
a)
31°C
b)
22°C
c)
19°C
d)
15°C

|
Arnav Iyer answered |
Let the final temperature be T Heat gained by ice = mL + m × s × (T – 0) = 10 × 80 + 10 × 1 × T
Heat lost by water = 55 × 1× (40 – T)
By using law of calorimetery, 800 + 10 T = 55 × (40 – T)
⇒ T = 21.54°C = 22°C
Heat lost by water = 55 × 1× (40 – T)
By using law of calorimetery, 800 + 10 T = 55 × (40 – T)
⇒ T = 21.54°C = 22°C
A black body has maximum wavelength λm at temperature 2000 K. Its corresponding wavelength at temperature 3000 K will be- a)

- b)
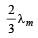
- c)
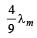
- d)

Correct answer is option 'B'. Can you explain this answer?
A black body has maximum wavelength λm at temperature 2000 K. Its corresponding wavelength at temperature 3000 K will be
a)

b)
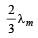
c)
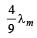
d)


|
Ayush Choudhury answered |
According to Wein's displacement law,
λmT = 2.88 × 10–3 When T = 2000 K,
λm (2000) = 2.88 × 10–3 ....(1)
When T = 3000 K, λ'm (3000) = 2.88 × 10–3 ....(2)
Dividing (1) by (2),
λm (2000) = 2.88 × 10–3 ....(1)
When T = 3000 K, λ'm (3000) = 2.88 × 10–3 ....(2)
Dividing (1) by (2),
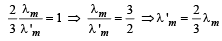
Wien's law is concerned with [2002]- a)relation between emissivity and absorptivity of a radiating surface
- b)total radiation, emitted by a hot surface
- c)an expression for spectral distribution of energy of a radiation from any source
- d)a relation between the temperature of a black body and the wavelength at which there is maximum radiant energy per unit wavelength
Correct answer is option 'D'. Can you explain this answer?
Wien's law is concerned with [2002]
a)
relation between emissivity and absorptivity of a radiating surface
b)
total radiation, emitted by a hot surface
c)
an expression for spectral distribution of energy of a radiation from any source
d)
a relation between the temperature of a black body and the wavelength at which there is maximum radiant energy per unit wavelength

|
Subhankar Datta answered |
According to Wein's displacement law, product of wavelength belonging to maximum intensity and temperature is constant i.e., λmT = constant.
Liquid oxygen at 50 K is heated to 300 K at constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time? [2012]- a)

- b)

- c)

- d)

Correct answer is option 'A'. Can you explain this answer?
Liquid oxygen at 50 K is heated to 300 K at constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time? [2012]
a)

b)

c)

d)


|
Harshitha Dey answered |
Initially liquid oxygen will gain the temperature up to its boiling temperature then it change its state to gas. After this again its temperature will increase, so corresponding graph will be
If the cold junction of a thermo-couple is kept at 0°C and the hot junction is kept at T°C then the relation between neutral temperature (Tn) and temperature of inversion (Ti) is [2007]- a)Tn = 2Ti
- b)Tn = Ti – T
- c)Tn = Ti + T
- d)Tn = Ti/2
Correct answer is option 'D'. Can you explain this answer?
If the cold junction of a thermo-couple is kept at 0°C and the hot junction is kept at T°C then the relation between neutral temperature (Tn) and temperature of inversion (Ti) is [2007]
a)
Tn = 2Ti
b)
Tn = Ti – T
c)
Tn = Ti + T
d)
Tn = Ti/2

|
Ruchi Chopra answered |
Since 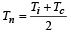 = Neutral temperature
= Neutral temperature
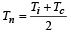 = Neutral temperature
= Neutral temperature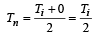
[Tc = 0°C = temperature of cold junction]
Mercury thermometer can be used to measure temperature upto [1992]- a)260°C
- b)100°C
- c)357°C
- d)500°C
Correct answer is option 'C'. Can you explain this answer?
Mercury thermometer can be used to measure temperature upto [1992]
a)
260°C
b)
100°C
c)
357°C
d)
500°C

|
Subhankar Datta answered |
Mercury thermometer is based on the principle of change of volume with rise of temperature and can measure temperatures ranging from –30°C to 357°C.
Which of the following circular rods (given radius r and length l), each made of the same material and whose ends are maintained at the same temperature will conduct most heat? [2005]- a)r = r0 ; l = l0
- b)r = 2r0 ; l = l0
- c)r = r0; l = 2l0
- d)r = 2r0; l = 2l0
Correct answer is option 'B'. Can you explain this answer?
Which of the following circular rods (given radius r and length l), each made of the same material and whose ends are maintained at the same temperature will conduct most heat? [2005]
a)
r = r0 ; l = l0
b)
r = 2r0 ; l = l0
c)
r = r0; l = 2l0
d)
r = 2r0; l = 2l0
|
|
Kumari Nandani answered |
A
A black body at 227°C radiates heat at the r ate of 7 cals/cm2s. At a temperature of 727°C, the rate of heat radiated in the same units will be:- a)50
- b)112 [2009]
- c)80
- d)60
Correct answer is option 'B'. Can you explain this answer?
A black body at 227°C radiates heat at the r ate of 7 cals/cm2s. At a temperature of 727°C, the rate of heat radiated in the same units will be:
a)
50
b)
112 [2009]
c)
80
d)
60

|
Moumita Khanna answered |
Accordin g to Stefan’s law E = σT4,
T1 = 500 K
T2 = 1000 K
T1 = 500 K
T2 = 1000 K
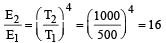
∴ E2 = 16 × 7 = 112 cal / cm2s
The total radiant energy per unit area, normal to the direction of incidence, received at a distance R from the centre of a star of radius r, whose outer surface radiates as a black body at a temperature T K is given by: [2010]- a)
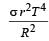
- b)
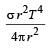
- c)
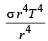
- d)
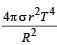
Correct answer is option 'A'. Can you explain this answer?
The total radiant energy per unit area, normal to the direction of incidence, received at a distance R from the centre of a star of radius r, whose outer surface radiates as a black body at a temperature T K is given by: [2010]
a)
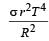
b)
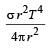
c)
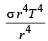
d)
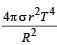

|
Mehul Iyer answered |
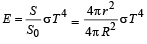
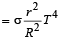
Assuming the sun to have a sph erical outer surface of radius r, radiating like a black body at temperature t°C, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is [2007] where σ is the Stefan’s constant.- a)
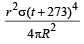
- b)
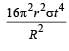
- c)
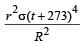
- d)
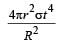
Correct answer is option 'C'. Can you explain this answer?
Assuming the sun to have a sph erical outer surface of radius r, radiating like a black body at temperature t°C, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is [2007] where σ is the Stefan’s constant.
a)
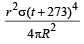
b)
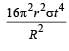
c)
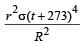
d)
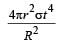

|
Dipika Das answered |
Power radiated by the sun at t°C
= σ(t + 273)44πr2
Power received by a unit surface
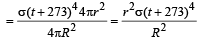
A beaker full of hot water is kept in a room. If it cools from 80°C to 75°C in t1 minutes, from 75° C to 70°C in t2 minutes and from 70°C to 65°C in t3 minutes, then [1995]- a)t1 = t2 = t3
- b)t1 < t2 = t3
- c)t1 < t2 < t3
- d)t1 > t2 > t3
Correct answer is option 'C'. Can you explain this answer?
A beaker full of hot water is kept in a room. If it cools from 80°C to 75°C in t1 minutes, from 75° C to 70°C in t2 minutes and from 70°C to 65°C in t3 minutes, then [1995]
a)
t1 = t2 = t3
b)
t1 < t2 = t3
c)
t1 < t2 < t3
d)
t1 > t2 > t3

|
Mrosmick Mani answered |
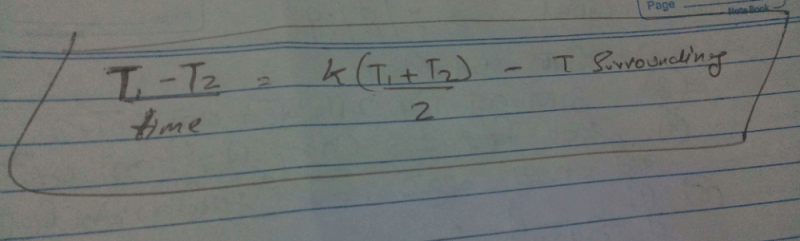
The coefficient of linear expansions of brass and steel are α1 and α2 respectively. When we take a brass rod of length ℓ1 and a steel rod of length ℓ2 at 0ºC, then the difference in their lengths (ℓ2 – ℓ1) will remain the same at all temperatures if [1995, 1999]- a)
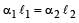
- b)
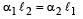
- c)
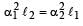
- d)
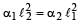
Correct answer is option 'A'. Can you explain this answer?
The coefficient of linear expansions of brass and steel are α1 and α2 respectively. When we take a brass rod of length ℓ1 and a steel rod of length ℓ2 at 0ºC, then the difference in their lengths (ℓ2 – ℓ1) will remain the same at all temperatures if [1995, 1999]
a)
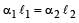
b)
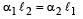
c)
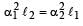
d)
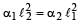

|
Krish Saha answered |
Let ΔT be increase in the temperature of brass wire.Then length of brass wire, 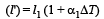
Similarly, length of steel wire when temperature is increased by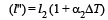 According to question , l' – l'' = l1 – l2
According to question , l' – l'' = l1 – l2
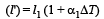
Similarly, length of steel wire when temperature is increased by
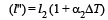 According to question , l' – l'' = l1 – l2
According to question , l' – l'' = l1 – l2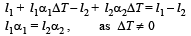
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperatures T1 and T2 (T1 > T2). The rate of heat transfer, 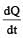 through the rod in a steady state is given by: [2009]
through the rod in a steady state is given by: [2009]- a)
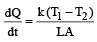
- b)
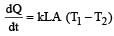
- c)
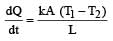
- d)
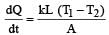
Correct answer is option 'C'. Can you explain this answer?
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperatures T1 and T2 (T1 > T2). The rate of heat transfer, 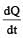 through the rod in a steady state is given by: [2009]
through the rod in a steady state is given by: [2009]
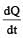 through the rod in a steady state is given by: [2009]
through the rod in a steady state is given by: [2009]a)
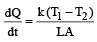
b)
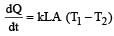
c)
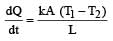
d)
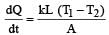

|
Krish Saha answered |
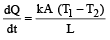
[(T1–T2) is the temperature difference]
On a new scale of temperature (which is linear) and called the W scale, the freezing and boiling points of water are 39° W and 239° W respectively. What will be the temperature on the new scale, corresponding to a temperature of 39° C on the Celsius scale? [2008]- a)78° W
- b)117° W
- c)200° W
- d)139° W
Correct answer is option 'B'. Can you explain this answer?
On a new scale of temperature (which is linear) and called the W scale, the freezing and boiling points of water are 39° W and 239° W respectively. What will be the temperature on the new scale, corresponding to a temperature of 39° C on the Celsius scale? [2008]
a)
78° W
b)
117° W
c)
200° W
d)
139° W

|
Abhishek Choudhary answered |
For different temperature scales, we have
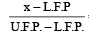 = constant
= constantWhere L.F.P ⇒ Lower Fixed point
U.H.F. ⇒ Upper fixed point
where x is the measurement at that scale.
Here, if C and W be the measurements on Celsius and W scale then,
U.H.F. ⇒ Upper fixed point
where x is the measurement at that scale.
Here, if C and W be the measurements on Celsius and W scale then,

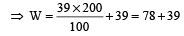
= 117° W
Chapter doubts & questions for Thermal Properties of Matter - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Thermal Properties of Matter - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

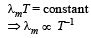


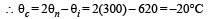

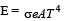
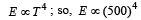
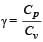 and R is theuniversal gas constant, then Cv is equal to [NEET 2013]
and R is theuniversal gas constant, then Cv is equal to [NEET 2013]