NEET Exam > NEET Questions > A slab of stone of area 0.36 m2 and thickness...
Start Learning for Free
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]
- a)1.24 J/m/s/°C
- b)1.29 J/m/s/°C
- c)2.05 J/m/s/°C
- d)1.02 J/m/s/°C
Correct answer is option 'A'. Can you explain this answer?
Verified Answer
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the ...

Rate of heat given by steam = Rate of heat taken by ice where
K = Thermal conductivity of the slab
m = Mass of the ice
L = Latent heat of melting/fusion
A = Area of the slab
K = Thermal conductivity of the slab
m = Mass of the ice
L = Latent heat of melting/fusion
A = Area of the slab

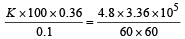
K =1.24 J/m/s/°C
Most Upvoted Answer
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the ...
°C. The upper surface is exposed to air at 25°C. The thermal conductivity of the stone is 2.5 W/mK. The density of the stone is 2500 kg/m3 and its specific heat capacity is 800 J/kgK.
We can use the following equation to calculate the rate of heat transfer through the slab:
Q/t = kA(T1 - T2)/L
where Q/t is the rate of heat transfer (in watts), k is the thermal conductivity (in watts per meter Kelvin), A is the area of the slab (in square meters), T1 is the temperature of the steam (in Kelvin), T2 is the temperature of the air (in Kelvin), and L is the thickness of the slab (in meters).
Plugging in the given values, we get:
Q/t = (2.5 W/mK)(0.36 m2)((100 + 273) K - (25 + 273) K)/(0.1 m) = 738 W
This means that 738 joules of heat are transferred through the slab every second.
To calculate the temperature of the slab at any given time, we need to use the following equation:
Q = mcΔT
where Q is the amount of heat transferred (in joules), m is the mass of the slab (in kilograms), c is the specific heat capacity of the stone (in joules per kilogram Kelvin), and ΔT is the change in temperature (in Kelvin).
We can rearrange this equation to solve for ΔT:
ΔT = Q/(mc)
Plugging in the given values, we get:
ΔT = 738 J/(2500 kg)(800 J/kgK) = 0.37 K
This means that the temperature of the slab will increase by 0.37 Kelvin every second. After a certain amount of time, the temperature of the slab will reach an equilibrium point where the rate of heat transfer into the slab equals the rate of heat transfer out of the slab. At this point, the temperature of the slab will be constant.
We can use the following equation to calculate the rate of heat transfer through the slab:
Q/t = kA(T1 - T2)/L
where Q/t is the rate of heat transfer (in watts), k is the thermal conductivity (in watts per meter Kelvin), A is the area of the slab (in square meters), T1 is the temperature of the steam (in Kelvin), T2 is the temperature of the air (in Kelvin), and L is the thickness of the slab (in meters).
Plugging in the given values, we get:
Q/t = (2.5 W/mK)(0.36 m2)((100 + 273) K - (25 + 273) K)/(0.1 m) = 738 W
This means that 738 joules of heat are transferred through the slab every second.
To calculate the temperature of the slab at any given time, we need to use the following equation:
Q = mcΔT
where Q is the amount of heat transferred (in joules), m is the mass of the slab (in kilograms), c is the specific heat capacity of the stone (in joules per kilogram Kelvin), and ΔT is the change in temperature (in Kelvin).
We can rearrange this equation to solve for ΔT:
ΔT = Q/(mc)
Plugging in the given values, we get:
ΔT = 738 J/(2500 kg)(800 J/kgK) = 0.37 K
This means that the temperature of the slab will increase by 0.37 Kelvin every second. After a certain amount of time, the temperature of the slab will reach an equilibrium point where the rate of heat transfer into the slab equals the rate of heat transfer out of the slab. At this point, the temperature of the slab will be constant.

|
Explore Courses for NEET exam
|

|
Question Description
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer?.
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A slab of stone of area 0.36 m2 and thickness 0.1 m is exposed on the lower surface to steam at 100°C. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of slab is : (Given latent heat of fusion of ice = 3.36 × 105 Jkg–1.) : [2012M]a)1.24 J/m/s/°Cb)1.29 J/m/s/°Cc)2.05 J/m/s/°Cd)1.02 J/m/s/°CCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.























