All Exams >
NEET >
NCERT Based Tests for NEET >
All Questions
All questions of Gravitation for NEET Exam
A man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface, he realizes that he will pass through a small hole in the planet. As he enters the hole, he sees that the planet is really made of two pieces a spherical shell of negligible thickness of mass 2M/3 and a point mass M/3 at the centre. Change in the force of gravity experienced by the man is- a)
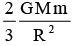
- b)0
- c)
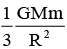
- d)
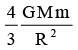
Correct answer is option 'A'. Can you explain this answer?
A man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface, he realizes that he will pass through a small hole in the planet. As he enters the hole, he sees that the planet is really made of two pieces a spherical shell of negligible thickness of mass 2M/3 and a point mass M/3 at the centre. Change in the force of gravity experienced by the man is
a)
b)
0
c)
d)
|
Shailja Jadon answered |
The gravitational force on the man when he was falling towards the planet was (GMm)/r^2. G here is the constant. M is mass of the whole planet ie M/3 + 2M/3. m is mass of the man. and r is the radius of the planet. once he has entered the hole in the planet. the force he was experiencing earlier due to the outer shell of the planet becomes 0. and now he experiences force only due to the point mass at the centre. this force is equal to (GMm)/3r^2. thus the change in force is initial - final force experienced which is equal to (2GMm)/3r^2. thus the answer.
Journey through the center of earth:
Suppose you could dig a tunnel from one surface to the opposite through the centre of the Earth. How will the journey be through the tunnel? Let us assume that the Earth to be of uniform density, there is no air friction and temperature is normal. At the starting point the initial acceleration will be g = 9.8 m/s2.
The acceleration gradually reduces as one approaches the center.
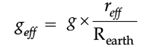The gravity at any radius reff is less than REarth and is linearly proportional to the distance from the center. So, the weight will goes on reducing as the centre is approached. It will again goes on increasing as one moves from away from the centre. The traveller will pop up on the opposite side of the Earth within 42 minutes approximately. But unless the traveller grabs something to hold on, he or she will fall back for a return journey and continue to oscillate with a round-trip time. The time period will be
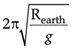Compare the weight of the traveller at point A and B inside the tunnel.- a)Weight at A > weight at B
- b)Weight at B > Weight at A
- c)Weight at A = Weight at B
- d)Weight at A = Weight at B = 0
Correct answer is option 'A'. Can you explain this answer?
Journey through the center of earth:
Suppose you could dig a tunnel from one surface to the opposite through the centre of the Earth. How will the journey be through the tunnel? Let us assume that the Earth to be of uniform density, there is no air friction and temperature is normal. At the starting point the initial acceleration will be g = 9.8 m/s2.
Suppose you could dig a tunnel from one surface to the opposite through the centre of the Earth. How will the journey be through the tunnel? Let us assume that the Earth to be of uniform density, there is no air friction and temperature is normal. At the starting point the initial acceleration will be g = 9.8 m/s2.
The acceleration gradually reduces as one approaches the center.
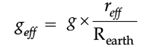
The gravity at any radius reff is less than REarth and is linearly proportional to the distance from the center. So, the weight will goes on reducing as the centre is approached. It will again goes on increasing as one moves from away from the centre. The traveller will pop up on the opposite side of the Earth within 42 minutes approximately. But unless the traveller grabs something to hold on, he or she will fall back for a return journey and continue to oscillate with a round-trip time. The time period will be
Compare the weight of the traveller at point A and B inside the tunnel.
a)
Weight at A > weight at B
b)
Weight at B > Weight at A
c)
Weight at A = Weight at B
d)
Weight at A = Weight at B = 0
|
Knowledge Hub answered |
The acceleration gradually reduce as one approaches the center of earth. The weight will reduce accordingly and will be zero at the center of the Earth.
Can you explain the answer of this question below:The value of escape velocity on earth when the body is thrown making an angle of 45o with the horizontal is
- A:
11.2 x 21/4 km/s
- B:
22.4 km/s
- C:
11.2 x 21/2 km/s
- D:
11.2 km/s
The answer is d.
The value of escape velocity on earth when the body is thrown making an angle of 45o with the horizontal is
11.2 x 21/4 km/s
22.4 km/s
11.2 x 21/2 km/s
11.2 km/s
|
Neha Joshi answered |
Escape velocity does not depend on the angle of projection. Escape velocity will remain the same.
Hence, escape velocity is 11.2km/s .
Hence, escape velocity is 11.2km/s .
Two uniform spherical stars made of same material have radii R and 2R. Mass of the smaller planet is m. They start moving from rest towards each other from a large distance under mutual force of gravity. The collision between the stars is inelastic with coefficient of restitution 1/2.Kinetic energy of the system just after the collision is- a)
- b)
- c)
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Two uniform spherical stars made of same material have radii R and 2R. Mass of the smaller planet is m. They start moving from rest towards each other from a large distance under mutual force of gravity. The collision between the stars is inelastic with coefficient of restitution 1/2.
Kinetic energy of the system just after the collision is
a)
b)
c)
d)
Cannot be determined
|
EduRev JEE answered |
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is- a)1:4
- b)4:1
- c)1:2
- d)2:1
Correct answer is 'B'. Can you explain this answer?
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is
a)
1:4
b)
4:1
c)
1:2
d)
2:1
|
Niharika Nair answered |
We know that the force of gravitation is inversely proportional to square of the distance between the two bodies,
i.e. F∝ r-2
Hence, when the distance between them will be doubled, the force will be reduced by 4 times
So, the ratio will be 4:1
Which is untrue about orbital velocity?
- a)increases with the increase in height of satellite
- b)depends on mass and radius of planet around which it revolves
- c)it is independent of mass of satellite
- d)decreases with an increase in radius of orbit
Correct answer is option 'A'. Can you explain this answer?
Which is untrue about orbital velocity?
a)
increases with the increase in height of satellite
b)
depends on mass and radius of planet around which it revolves
c)
it is independent of mass of satellite
d)
decreases with an increase in radius of orbit
|
Om Desai answered |
The untrue statement about orbital velocity is:
1. increases with the increase in height of satellite
Explanation: Orbital velocity is the speed at which an object revolves around a planet or other celestial body in a stable orbit. According to the equation for orbital velocity, v = √(GM/r+h), where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
As the height of the satellite increases (meaning it gets far to the planet), its h increase , so reasulting in decrease in velocity .
The other statements are true:
2. depends on mass and radius of planet around which it revolves: As mentioned in the equation, orbital velocity depends on both the mass (M) of the planet and the radius (r) of the orbit.
3. it is independent of mass of satellite: The mass of the satellite does not appear in the equation for orbital velocity, so it does not affect the speed at which the satellite orbits the planet.
4. decreases with an increase in radius of orbit: From the equation, we can see that as the radius of the orbit (r) increases, the orbital velocity (v) decreases.
1. increases with the increase in height of satellite
Explanation: Orbital velocity is the speed at which an object revolves around a planet or other celestial body in a stable orbit. According to the equation for orbital velocity, v = √(GM/r+h), where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
As the height of the satellite increases (meaning it gets far to the planet), its h increase , so reasulting in decrease in velocity .
The other statements are true:
2. depends on mass and radius of planet around which it revolves: As mentioned in the equation, orbital velocity depends on both the mass (M) of the planet and the radius (r) of the orbit.
3. it is independent of mass of satellite: The mass of the satellite does not appear in the equation for orbital velocity, so it does not affect the speed at which the satellite orbits the planet.
4. decreases with an increase in radius of orbit: From the equation, we can see that as the radius of the orbit (r) increases, the orbital velocity (v) decreases.
With what angular velocity the earth should spin in order that a body lying at 30° latitude may become weightless [R is radius of earth and g is acceleration due to gravity on the surface of earth]- a)
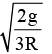
- b)
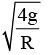
- c)
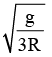
- d)
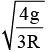
Correct answer is option 'D'. Can you explain this answer?
With what angular velocity the earth should spin in order that a body lying at 30° latitude may become weightless [R is radius of earth and g is acceleration due to gravity on the surface of earth]
a)
b)
c)
d)
|
|
Nandini Iyer answered |
g' = acceleration due to gravity at latitude
g = acceleration due to gravity at poles
ω = angular velocity of earth
(θ) = latitude angle
Now,
g' = g - Rω^2 cos^2(θ)
As, g' = 0 (weightless):
g = Rω^2 cos^2(θ)
g = Rω^2 cos^2(30)
g = Rω^2 (3/4)
ω^2 = 4g/3R
ω = √(4g/3R)
g = acceleration due to gravity at poles
ω = angular velocity of earth
(θ) = latitude angle
Now,
g' = g - Rω^2 cos^2(θ)
As, g' = 0 (weightless):
g = Rω^2 cos^2(θ)
g = Rω^2 cos^2(30)
g = Rω^2 (3/4)
ω^2 = 4g/3R
ω = √(4g/3R)
At what altitude will the acceleration due to gravity be 25% of that at the earth’s surface (given radius of earth is R)?- a)R/4
- b)R
- c)3R/8
- d)R/2
Correct answer is option 'B'. Can you explain this answer?
At what altitude will the acceleration due to gravity be 25% of that at the earth’s surface (given radius of earth is R)?
a)
R/4
b)
R
c)
3R/8
d)
R/2
|
|
Neha Sharma answered |
Force on the body placed on Earth's surface is
F=GMm/R2
But, F=mg hence,
mg=GMm/R2
where, variables have their usual meanings.
gR2=GM
Now, force on the body at geo-potential height say h (altitude) where the acceleration due to gravity is 25% of that at the earth's surface i.e.
25g/100=g/4
Hence, we can write
g/4=GM/(R+h)2
g/4= gR2 /(R+h)2
(R+h)2=4R2
Taking roots for both sides we get
R+h=2R
h=R
F=GMm/R2
But, F=mg hence,
mg=GMm/R2
where, variables have their usual meanings.
gR2=GM
Now, force on the body at geo-potential height say h (altitude) where the acceleration due to gravity is 25% of that at the earth's surface i.e.
25g/100=g/4
Hence, we can write
g/4=GM/(R+h)2
g/4= gR2 /(R+h)2
(R+h)2=4R2
Taking roots for both sides we get
R+h=2R
h=R
What does the term escape speed of a planet mean?- a)the minimum speed of an object to reach a height equal to the radius of the planet
- b)cannot be defined
- c)the minimum speed required for an object to reach infinity
- d)the maximum speed required for an object to reach infinity
Correct answer is option 'C'. Can you explain this answer?
What does the term escape speed of a planet mean?
a)
the minimum speed of an object to reach a height equal to the radius of the planet
b)
cannot be defined
c)
the minimum speed required for an object to reach infinity
d)
the maximum speed required for an object to reach infinity
|
|
Om Desai answered |
Escape velocity is the minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own.
A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is V. Due to the rotation of planet about its axis the acceleration due to gravity g at equator is 1/2 of g at poles. The escape velocity of a particle on the pole of planet in terms of V.- a)Ve = 2V
- b)Ve= V
- c)Ve= V/2
- d)Ve =
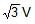
Correct answer is option 'A'. Can you explain this answer?
A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is V. Due to the rotation of planet about its axis the acceleration due to gravity g at equator is 1/2 of g at poles. The escape velocity of a particle on the pole of planet in terms of V.
a)
Ve = 2V
b)
Ve= V
c)
Ve= V/2
d)
Ve =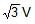
|
Mohit Rajpoot answered |
India’s first artificial satellite was:- a)Sputnik
- b)Rohini
- c)Insat
- d)Aryabhatta
Correct answer is option 'D'. Can you explain this answer?
India’s first artificial satellite was:
a)
Sputnik
b)
Rohini
c)
Insat
d)
Aryabhatta
|
Geetika Shah answered |
India's first artificial satellite was Aryabhata. Launched by soviet union on 19 April 1975
An unmanned space probe is to the thrown with such a velocity that it does not return to earth. It should be thrown with- a)velocity ≥ (2GM/ R)1/2
- b)a great velocity but nothing more can be said
- c)velocity >(2GM)1/2/ R necessarily
- d)only the velocity = (2GM)1/2/R
Correct answer is option 'A'. Can you explain this answer?
An unmanned space probe is to the thrown with such a velocity that it does not return to earth. It should be thrown with
a)
velocity ≥ (2GM/ R)1/2
b)
a great velocity but nothing more can be said
c)
velocity >(2GM)1/2/ R necessarily
d)
only the velocity = (2GM)1/2/R
|
Riya Banerjee answered |
It should be thrown with a velocity greater than or equal to escape velocity of the planet only then it will not return to Earth
Escape Velocity = √(2GM/R) = (2GM/R)1/2
Hence A is the correct answer.
Escape Velocity = √(2GM/R) = (2GM/R)1/2
Hence A is the correct answer.
A satellite which appears to be at a fixed position at a definite height to an observer is called:- a)Geostationary satellite and geosynchronous satellite
- b)Polar satellite
- c)Geostationary satellite
- d)Geosynchronous satellite
Correct answer is option 'A'. Can you explain this answer?
A satellite which appears to be at a fixed position at a definite height to an observer is called:
a)
Geostationary satellite and geosynchronous satellite
b)
Polar satellite
c)
Geostationary satellite
d)
Geosynchronous satellite
|
|
Neha Joshi answered |
As the relative velocity of the satellite with respect to the earth is zero, it appears stationary from the Earth surface and therefore it is called is geostationary satellite or geosynchronous satellite.
The escape velocity for the moon is nearly- a)11.2km/s
- b)2.4km/s
- c)24km/s
- d)10km/s
Correct answer is option 'B'. Can you explain this answer?
The escape velocity for the moon is nearly
a)
11.2km/s
b)
2.4km/s
c)
24km/s
d)
10km/s
|
|
Rohit Shah answered |
About 11.2 km/s
In common usage, the initial point is on the surface of a planet or moon. On the surface of the Earth, the escape velocity is about 11.2 km/s, which is approximately 33 times the speed of sound (Mach 33) and several times the muzzle velocity of a rifle bullet (up to 1.7 km/s).
Four particles, each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction. (Take that gravitational force between two point masses m1 and m2 separated by is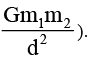 
The speed of each particle is- a)
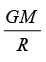
- b)
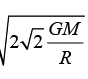
- c)
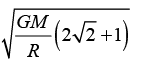
- d)
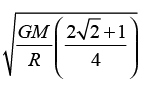
Correct answer is option 'D'. Can you explain this answer?
Four particles, each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction. (Take that gravitational force between two point masses m1 and m2 separated by is 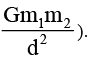The speed of each particle is
The speed of each particle isa)
b)
c)
d)
|
Lohit Matani answered |
The resultant of these two forces is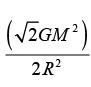 
.Now 
.Now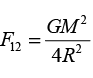 
Assuming the earth to be a sphere of uniform density the acceleration due to gravity- a)At a point outside the earth is inversely proportional to the square of its distance from the center
- b) At a point outside the earth is inversely proportional to its distance from the centre
- c)At a point inside is zero
- d)At a point inside is proportional to its distance from the centre
Correct answer is option 'A,D'. Can you explain this answer?
Assuming the earth to be a sphere of uniform density the acceleration due to gravity
a)
At a point outside the earth is inversely proportional to the square of its distance from the center
b)
At a point outside the earth is inversely proportional to its distance from the centre
c)
At a point inside is zero
d)
At a point inside is proportional to its distance from the centre
|
Krishna Iyer answered |
As g is inversely proportional to (R+h)2 when we go away from earth's surface g is inversely proportional to square of the distance and g is directly proportional to (R-d) when we go inside the surface of Earth therefore g is directly proportional to distance travelled inside the Earth
g=Gmr/a3=r for r<R
g=Gm/a2 for r<R
g=Gmr/a3=r for r<R
g=Gm/a2 for r<R
Titania, the largest moon of the planet Uranus, has 1/8 the radius of the earth and 1/1700 the mass of the earth. What is the acceleration due to gravity at the surface of TitaniaData: G = 6.67x10−11 N m2/kg, RE = 6.38 x 106 m, mE = 5.97 x 1024 kg- a)0.43 m/s2 Hz
- b)0.18 m/s2
- c)0.28 m/s2
- d)0.37 m/s2
Correct answer is option 'D'. Can you explain this answer?
Titania, the largest moon of the planet Uranus, has
1/8
the radius of the earth and 1/1700 the mass of the earth. What is the acceleration due to gravity at the surface of TitaniaData: G = 6.67x
10−11
N m2/kg, RE = 6.38 x 106
m, mE = 5.97 x 1024
kga)
0.43 m/s2 Hz
b)
0.18 m/s2
c)
0.28 m/s2
d)
0.37 m/s2
|
Suresh Iyer answered |
We know that gravitational acceleration, g = GM/R2
We know that M = Mass of earth /1700 and R = Radius of earth /8
Hence we get g = 64/1700 times the gravitational acceleration of earth
I.e. g = 64/1700 x 9.8
= 0.37 m/s2
We know that M = Mass of earth /1700 and R = Radius of earth /8
Hence we get g = 64/1700 times the gravitational acceleration of earth
I.e. g = 64/1700 x 9.8
= 0.37 m/s2
A geostationary satellite is at a height h above the surface of earth. If earth radius is R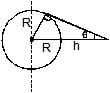 
- a)The minimum colatitude on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
- b)The maximum colatitudes on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
- c)The area on earth escaped from this satellite is given as 2pR2(1 + sinq)
- d) The area on earth escaped from this satellite is given as 2pR2(1 + cosq)
Correct answer is option 'A,C'. Can you explain this answer?
A geostationary satellite is at a height h above the surface of earth. If earth radius is R
a)
The minimum colatitude on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
b)
The maximum colatitudes on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
c)
The area on earth escaped from this satellite is given as 2pR2(1 + sinq)
d)
The area on earth escaped from this satellite is given as 2pR2(1 + cosq)
|
|
Knowledge Hub answered |
Minimum colatitude=sin θ=R/R+h
θ=sin-1(R/R+h)
The curved area AB on earth =2πR2(1−sinθ)
Area on earth escaped from satellite =4πR2−2πR2(1−sinθ)
=2πR2(1+sinθ)
θ=sin-1(R/R+h)
The curved area AB on earth =2πR2(1−sinθ)
Area on earth escaped from satellite =4πR2−2πR2(1−sinθ)
=2πR2(1+sinθ)
Two masses m1 & m2 are initially at rest and are separated by a very large distance. If the masses approach each other subsequently, due to gravitational attraction between them, their relative velocity of approach at a separation distance of d is :- a)
- b)
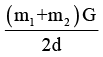
- c)
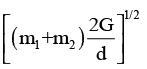
- d)
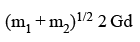
Correct answer is option 'C'. Can you explain this answer?
Two masses m1 & m2 are initially at rest and are separated by a very large distance. If the masses approach each other subsequently, due to gravitational attraction between them, their relative velocity of approach at a separation distance of d is :
a)
b)
c)
d)
|
|
Neha Joshi answered |
We use the energy balance
Initial potential energy equals final kinetic energy
Gm1m2/d=1mv12/2+1mv22/2
also, from the conservation of momentum we have
m1v1=m2v2
or
v1= m1v1/ m2
Substituting this we get
v1=√2Gm22/d(m1+m2)
Similarly, we have
v2= √2Gm12/ d(m1+m2)
Now as velocities are in opposite direction their relative velocity is v1−(−v2)=v1+v2
or
[2G(m1+m2)/ d]1/2
Initial potential energy equals final kinetic energy
Gm1m2/d=1mv12/2+1mv22/2
also, from the conservation of momentum we have
m1v1=m2v2
or
v1= m1v1/ m2
Substituting this we get
v1=√2Gm22/d(m1+m2)
Similarly, we have
v2= √2Gm12/ d(m1+m2)
Now as velocities are in opposite direction their relative velocity is v1−(−v2)=v1+v2
or
[2G(m1+m2)/ d]1/2
The gravitational potential due to the gravitational force on the earth is defined as the- a)potential energy multiplied by the mass of the object
- b)potential energy of the mass placed at that point
- c)numerically equal to the potential energy
- d)potential energy of a unit mass at that point.
Correct answer is option 'D'. Can you explain this answer?
The gravitational potential due to the gravitational force on the earth is defined as the
a)
potential energy multiplied by the mass of the object
b)
potential energy of the mass placed at that point
c)
numerically equal to the potential energy
d)
potential energy of a unit mass at that point.
|
|
Nandini Patel answered |
Gravitational Potential
Gravitational Potential is dened as the potential energy of a particle of unit mass at that point due to the gravitational force exerted byearth. Gravitational potential energy of a unit mass is known as gravitational potential.
Gravitational Potential is:- a)negative, scalar quantity , unit JKg-1
- b)positive, vector quantity , unit JKg-1
- c)positive, scalar quantity , unit JKg-1
- d)negative, vector quantity , unit JKg-1
Correct answer is option 'A'. Can you explain this answer?
Gravitational Potential is:
a)
negative, scalar quantity , unit JKg-1
b)
positive, vector quantity , unit JKg-1
c)
positive, scalar quantity , unit JKg-1
d)
negative, vector quantity , unit JKg-1
|
Ayush Joshi answered |
Gravitational potential (radial fields) at a point in a radial field is the work done per unit mass against the field, in bringing a small mass from infinite distance to the point. Since gravitational fields are attractive and the potential at infinite distance is zero, all points within the field have negative values of potential. Gravitational potential is a scalar quantity with SI unit J kg^-1. The symbol used is mostly V but sometimes or Vr or V(r). A radial gravitational field is one in which the field strength has the same magnitude at all points at a given distance from the center.
According to Kepler’s Law of orbits:- a)All planets move in parabolic orbits with the Earth situated at one of the foci of the parabola.
- b)All planets move in elliptical orbits with the earth situated at one of the foci of the ellipse.
- c)All planets move in elliptical orbits with the Sun situated at one of the foci of the ellipse
- d)All planets move in parabolic orbits with the Sun situated at one of the foci of the parabola.
Correct answer is option 'C'. Can you explain this answer?
According to Kepler’s Law of orbits:
a)
All planets move in parabolic orbits with the Earth situated at one of the foci of the parabola.
b)
All planets move in elliptical orbits with the earth situated at one of the foci of the ellipse.
c)
All planets move in elliptical orbits with the Sun situated at one of the foci of the ellipse
d)
All planets move in parabolic orbits with the Sun situated at one of the foci of the parabola.
|
Muskaan Mishra answered |
Explanation:The orbit of a planet around the Sun (or of a satellite around a planet) is not a perfect circle. It is an ellipse—a “flattened” circle. The Sun (or the centre of the planet) occupies one focus of the ellipse. A focus is one of the two internal points that help determine the shape of an ellipse. The distance from one focus to any point on the ellipse and then back to the second focus is always the same.
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is- a) R/2
- b)2R
- c)R/3
- d)3R
Correct answer is option 'B'. Can you explain this answer?
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is
a)
R/2
b)
2R
c)
R/3
d)
3R
|
|
Ritu Singh answered |
Acceleration due to gravity at a height “h” is given by
g’ = g (R/R+h)2
Here,
g is the acceleration due to gravity on the surface
R is the radius of the earth
As g’ is given as g/9, we get
g/9 = g(R/R+h)2
⅓ = R/(R+h)
h=2R
Satellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is- a)1 : 2
- b)1 : 4
- c)1 : 8
- d)1 : 16
Correct answer is option 'A'. Can you explain this answer?
Satellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is
a)
1 : 2
b)
1 : 4
c)
1 : 8
d)
1 : 16
|
|
Gaurav Kumar answered |
Answer :- a
Solution :- L = mvr
⇒L=m√GMr/r
L = m√GMr−−−−.....(1)
L = 2mdA/dt....(2)
From (1) and (2)
dA/dt ∝ (r)^1/2
= √(dA/dt)1/(dA/dt)2
= √4/1 = 2/1
How much deep inside the earth should a man go so that his weight becomes one fourth of that at a point which is at a height R above the surface of earth .- a)R/4
- b)15R/16
- c)3R/4
- d) R/2
Correct answer is option 'B'. Can you explain this answer?
How much deep inside the earth should a man go so that his weight becomes one fourth of that at a point which is at a height R above the surface of earth .
a)
R/4
b)
15R/16
c)
3R/4
d)
R/2
|
Hansa Sharma answered |
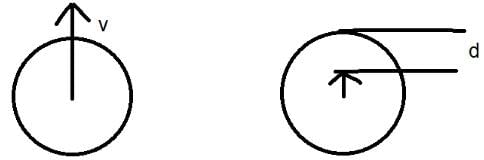
g=GM/r2 g1=GMr/R3
we are given that,
GMr/R3 =(1/4) GM/(R+R)2
=>r/R3=(1/4).(1/4R2)
=>r=R/6
Therefore, d=R-r=15R/16
The acceleration due to gravity at the North Pole of Neptune is approximately 10.7 x m/s2. Neptune has mass 1.0 x 1026 kg and radius 2.5 x 104 km and rotates once around its axis in about 16 h. What is the apparent weight a 5.0-kg object at Neptune’s equator?- a)51 N
- b)49 N
- c)50 N
- d)52 N
Correct answer is option 'D'. Can you explain this answer?
The acceleration due to gravity at the North Pole of Neptune is approximately 10.7 x m/s2. Neptune has mass 1.0 x
1026
kg and radius 2.5 x 104
km and rotates once around its axis in about 16 h. What is the apparent weight a 5.0-kg object at Neptune’s equator?a)
51 N
b)
49 N
c)
50 N
d)
52 N
|
Puja Kaur answered |
To find the resultant gravitational force acting on the particle m due to a number of masses we need to use:- a)the principle of no action
- b)the principle of maximal action
- c)the principle of superposition
- d)the principle of least action
Correct answer is option 'C'. Can you explain this answer?
To find the resultant gravitational force acting on the particle m due to a number of masses we need to use:
a)
the principle of no action
b)
the principle of maximal action
c)
the principle of superposition
d)
the principle of least action
|
|
Reena Dhanesh Kumar answered |
Refer ncert u have a gud definition
If a tunnel is cut at any orientation through earth, then a ball released from one end will reach the other end in time (neglect earth rotation)- a)84.6 minutes
- b)42.3 minutes
- c)8 minutes
- d)Depends on orientation
Correct answer is option 'B'. Can you explain this answer?
If a tunnel is cut at any orientation through earth, then a ball released from one end will reach the other end in time (neglect earth rotation)
a)
84.6 minutes
b)
42.3 minutes
c)
8 minutes
d)
Depends on orientation
|
|
Neha Joshi answered |
Total time period will be 84.6 min when ball released from one end and it come backs to same point as in oscillation.
When ball is released from one end then time taken to reach other end will be half of total time period then that will be 42.3 min.
When ball is released from one end then time taken to reach other end will be half of total time period then that will be 42.3 min.
A satellite of mass 5M orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass M and the other of mass 4M. After the explosion the mass M ends up travelling in the same circular orbit, but in opposite direction. After explosion the mass 4M is in- a)Bound orbit
- b)Unbound orbit
- c)Partially bound orbit
- d)Data is insufficient to determine the nature of the orbit
Correct answer is option 'B'. Can you explain this answer?
A satellite of mass 5M orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass M and the other of mass 4M. After the explosion the mass M ends up travelling in the same circular orbit, but in opposite direction. After explosion the mass 4M is in
a)
Bound orbit
b)
Unbound orbit
c)
Partially bound orbit
d)
Data is insufficient to determine the nature of the orbit
|
|
Suresh Reddy answered |
Applying the conservation of momentum, we get:
V = velocity of 5M, V1 = velocity of 4M, V2 = velocity of M and ATQ V2 = -V
5MV = 4MV1 + M(-V)
6MV = 4MV1
V1 = 3/2 V
Now, Vo = orbital velocity and Ve = escape velocity
Ve = √2 Vo
In a bound orbit the object is gravitationally bound to the body that is the source of gravity (like the Earth is bound to the Sun, or the Moon to the Earth). An unbound orbit is typically hyperbolic, and the object will escape from the source of gravity
V = velocity of 5M, V1 = velocity of 4M, V2 = velocity of M and ATQ V2 = -V
5MV = 4MV1 + M(-V)
6MV = 4MV1
V1 = 3/2 V
Now, Vo = orbital velocity and Ve = escape velocity
Ve = √2 Vo
In a bound orbit the object is gravitationally bound to the body that is the source of gravity (like the Earth is bound to the Sun, or the Moon to the Earth). An unbound orbit is typically hyperbolic, and the object will escape from the source of gravity
The orbit of a planet P round the sun S. AB and CD are the minor and major axes of the ellipse.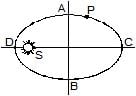 
If t1 is the time taken by the planet to travel along ACB and t2 the time along BDA, then- a) t1 = t2
- b)t1 > t2
- c) t1 < t2
- d)Nothing can be concluded
Correct answer is option 'B'. Can you explain this answer?
The orbit of a planet P round the sun S. AB and CD are the minor and major axes of the ellipse.
If t1 is the time taken by the planet to travel along ACB and t2 the time along BDA, then
a)
t1 = t2
b)
t1 > t2
c)
t1 < t2
d)
Nothing can be concluded
|
Pooja Shah answered |
Here, the angular momentum is conserved i.e. mvr is constant. Where r is the distance from centre of the sun to centre of the planet.
Now, consider one point each from both the mentioned paths. (Shown in fig.)
Applying conservation of angular momentum for these points we get
mv1r1=mv2r2. Simplifying this, v1/v2=r2/r1<1
Time period are given by
t1=L/ v1, t2= L/ v2
Comparing them by taking the ratio
t1/t2=(L/ v1)×(v2/L)
So, t1/t2=v2/v1>1.Thus t1>t2
Now, consider one point each from both the mentioned paths. (Shown in fig.)
Applying conservation of angular momentum for these points we get
mv1r1=mv2r2. Simplifying this, v1/v2=r2/r1<1
Time period are given by
t1=L/ v1, t2= L/ v2
Comparing them by taking the ratio
t1/t2=(L/ v1)×(v2/L)
So, t1/t2=v2/v1>1.Thus t1>t2
When a satellite moves in a circular orbit, the _______acceleration is provided by the gravitational attraction of the earth- a)tangential
- b)centrifugal
- c)centripetal
- d)fictitious
Correct answer is option 'C'. Can you explain this answer?
When a satellite moves in a circular orbit, the _______acceleration is provided by the gravitational attraction of the earth
a)
tangential
b)
centrifugal
c)
centripetal
d)
fictitious
|
|
Hansa Sharma answered |
When any body or particle moves in circular orbit centripetal force acts on it and to move the object centripetal acceleration is necessary. So, when a satellite moves in circular orbit the centripetal acceleration is provided by the gravitational attraction of the earth.
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre- a)Increases
- b) Decreases
- c) Remains same
- d)Ruring the compression increases then returns at the previous value
Correct answer is option 'B'. Can you explain this answer?
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
a)
Increases
b)
Decreases
c)
Remains same
d)
Ruring the compression increases then returns at the previous value
|
|
Suresh Iyer answered |
Gravitational Potential V = -GM/R for hollow spherical shell at the centre. If we replace R by R/2 then we get V = -2GM/R. Therefore it decreases.
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is- a)Mg/h
- b)
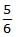mgh - c)
mgh - d)
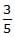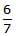mgh
Correct answer is option 'B'. Can you explain this answer?
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
a)
Mg/h
b)
mgh c)
mghd)
mgh|
|
Suresh Iyer answered |
Initial PE = -GMm/R
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?- a)
second - b)
seconds - c)
second - d)
second
Correct answer is option 'B'. Can you explain this answer?
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?
a)
secondb)
secondsc)
secondd)
second|
|
Pooja Shah answered |
As Mp=2Me and Dp=2De
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
In side a hollow spherical shell- a)Everywhere gravitational potential is zero
- b)Everywhere gravitational field is zero
- c) Everywhere gravitational potential is same
- d)Everywhere gravitational field is same
Correct answer is option 'B,C,D'. Can you explain this answer?
In side a hollow spherical shell
a)
Everywhere gravitational potential is zero
b)
Everywhere gravitational field is zero
c)
Everywhere gravitational potential is same
d)
Everywhere gravitational field is same
|
Lavanya Menon answered |
The gravitational field inside a uniform spherical shell is 0 from gauss law for gravitation since no mass is enclosed in any Gaussian surface.
Since gravitational potential is given by φ=−∫ gdr, hence, φ=constant since g=0.
Since the gravitational field is 0 everywhere, it is apparently the same everywhere.
Answer is B,C,D.
Since gravitational potential is given by φ=−∫ gdr, hence, φ=constant since g=0.
Since the gravitational field is 0 everywhere, it is apparently the same everywhere.
Answer is B,C,D.
A communications Earth satellite- a)Goes round the earth from east to west
- b)Can be in the equatorial plane only
- c)Can be vertically above any place on the earth
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A communications Earth satellite
a)
Goes round the earth from east to west
b)
Can be in the equatorial plane only
c)
Can be vertically above any place on the earth
d)
none of these
|
|
Pooja Shah answered |
Communication satellites are supposed to be geostationary in nature. So, from the above properties options B is correct.
Weightlessness is:- a)a situation in which the effective weight of the body becomes zero
- b)a situation in which the effective weight of the body becomes 10N
- c)a situation in which the effective weight of the body becomes 9.8N.
- d)a situation in which the effective mass of the body becomes zero
Correct answer is option 'A'. Can you explain this answer?
Weightlessness is:
a)
a situation in which the effective weight of the body becomes zero
b)
a situation in which the effective weight of the body becomes 10N
c)
a situation in which the effective weight of the body becomes 9.8N.
d)
a situation in which the effective mass of the body becomes zero
|
Akshay Shah answered |
Weight becomes zero in a freefall or when the total force on your body is zero.For example in a freely falling lift the contact force on your body is zero,so the wieghting machine would show zero reading.so you are wieghtless.
Consider two configurations of a system of three particles of masses m, 2m and 3m. The work done by external agent in changing the configuration of the system from figure (i) to figure (ii) is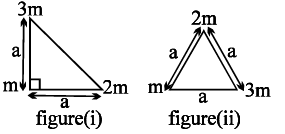
- a)zero
- b)
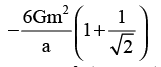
- c)
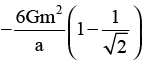
- d)
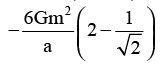
Correct answer is option 'C'. Can you explain this answer?
Consider two configurations of a system of three particles of masses m, 2m and 3m. The work done by external agent in changing the configuration of the system from figure (i) to figure (ii) is
a)
zero
b)
c)
d)
|
Arjun Singh answered |
Pick up either 2m or 3m mass for both configuration as the distance of other masses with respect to these is changing and find the sum of potential energy on that particular mass in both configurations subtract initial energy from final energy you will get answer
An earth satellite is moved from one stable circular orbit to a farther stable circular orbit. which one of following quantity increases- a)gravitational potential energy
- b)centripetal acceleration
- c)gravitationl force
- d)linear orbital speed
Correct answer is option 'A'. Can you explain this answer?
An earth satellite is moved from one stable circular orbit to a farther stable circular orbit. which one of following quantity increases
a)
gravitational potential energy
b)
centripetal acceleration
c)
gravitationl force
d)
linear orbital speed
|
|
Neha Joshi answered |
We know that gravitational potential is negative in sign and its magnitude decreases when distance from the massive attracting object increases, hence when considered with sign we can say that gravitational potential increases with increases in distance.
Escape velocity is:- a)The minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own.
- b)The minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and returns back
- c)The maximum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and returns back.
- d)The maximum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own
Correct answer is option 'A'. Can you explain this answer?
Escape velocity is:
a)
The minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own.
b)
The minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and returns back
c)
The maximum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and returns back.
d)
The maximum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own
|
|
Geetika Shah answered |
Escape velocity is the minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own.
What could be the maximum value for gravitational potential energy?- a)1
- b)zero
- c)infinity
- d)1000
Correct answer is option 'B'. Can you explain this answer?
What could be the maximum value for gravitational potential energy?
a)
1
b)
zero
c)
infinity
d)
1000
|
|
Riya Banerjee answered |
As, U=−Gm1m2/r,
it can be used to describe the potential energy in a system of point charges (or radially symmetric spheres) as a function of their separation distance r, then the maximum value is zero at infinite separation.
Hence, its maximum value is zero at infinity.
it can be used to describe the potential energy in a system of point charges (or radially symmetric spheres) as a function of their separation distance r, then the maximum value is zero at infinite separation.
Hence, its maximum value is zero at infinity.
When a satellite in a circular orbit around the earth enters the atmospheric region, it encounters small air resistance to its motion. Then- a) Its kinetic energy increases
- b)Its kinetic energy decreases
- c)Its angular momentum about the earth decreases
- d)Its period of revolution around the earth increases
Correct answer is option 'A'. Can you explain this answer?
When a satellite in a circular orbit around the earth enters the atmospheric region, it encounters small air resistance to its motion. Then
a)
Its kinetic energy increases
b)
Its kinetic energy decreases
c)
Its angular momentum about the earth decreases
d)
Its period of revolution around the earth increases
|
|
Hansa Sharma answered |
Due to air drag some mechanical energy of satellite will converted into heat energy, there will be loss of ME of satellite, so radius of orbit will decrease and satellite will follow a spiral path towards earth.
If r is decreases,
P.E.=−GMm/r, P.E. is also decreases.
K.E=GMm/2r K.E increasing, increased speed in spite of decrease in M.E. But rate of P.E decreases is more than the rate at which M.E decreases.
Angular momentum L=mrv=mr√GMr=m√GMr⇒L∝√r.
So, angular momentum decreases as r decreases.
If r is decreases,
P.E.=−GMm/r, P.E. is also decreases.
K.E=GMm/2r K.E increasing, increased speed in spite of decrease in M.E. But rate of P.E decreases is more than the rate at which M.E decreases.
Angular momentum L=mrv=mr√GMr=m√GMr⇒L∝√r.
So, angular momentum decreases as r decreases.
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 x 108 km.- a)2.4 x 1030 kg
- b)1.8 x 1030 kg
- c)2 x 1030 kg
- d)2.2 x 1030 kg
Correct answer is option 'C'. Can you explain this answer?
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 x 108 km.
a)
2.4 x 1030 kg
b)
1.8 x 1030 kg
c)
2 x 1030 kg
d)
2.2 x 1030 kg
|
Vaishnavi Bajaj answered |
R = Radius of Orbit of earth = 1.5 x 108 km = 1.5 x 1011m
T = time Period of earth around the sun = 365 Days
In Cavendish’s experiment,- a)torque on bar AB having two small lead spheres due to gravitational forces is balanced by the restoring torque of the wire
- b)net force on bar AB having two small lead spheres due to gravitational forces is positive
- c)net force on bar AB having two small lead spheres due to gravitational forces is negative
- d)net torque on bar AB having two small lead spheres due to gravitational forces is positive
Correct answer is option 'A'. Can you explain this answer?
In Cavendish’s experiment,
a)
torque on bar AB having two small lead spheres due to gravitational forces is balanced by the restoring torque of the wire
b)
net force on bar AB having two small lead spheres due to gravitational forces is positive
c)
net force on bar AB having two small lead spheres due to gravitational forces is negative
d)
net torque on bar AB having two small lead spheres due to gravitational forces is positive
|
Gowri Kulkarni answered |
Cavendish's apparatus for experimentally determining the value of G involved a light, rigid rod about 2-feet long. Two small lead spheres were attached to the ends of the rod and the rod was suspended by a thin wire. When the rod becomes twisted, the torsion of the wire begins to exert a torsional force that is proportional to the angle of rotation of the rod. The more twist of the wire, the more the system pushes backwards to restore itself towards the original position.
If a film of width l is stretched in the longitudinal direction a distance d by force F, surface tension is given by- a)S = F/l
- b)S = F/3l
- c)S = F/4l
- d)S = F/2l
Correct answer is option 'D'. Can you explain this answer?
If a film of width l is stretched in the longitudinal direction a distance d by force F, surface tension is given by
a)
S = F/l
b)
S = F/3l
c)
S = F/4l
d)
S = F/2l
|
|
Hansa Sharma answered |
- Let L be the width of the film. Since the film has two surfaces, the total length along which the surface force acts on the slider is 2L.
- The surface tension S in the film is defined as the ratio of the surface force F to the length d (perpendicular to the force) along which the force acts S=F/d
- Hence, in the case, d = 2L S=F/2L
If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g the same?- a)1/25
- b)1/5
- c)1
- d)5
Correct answer is option 'B'. Can you explain this answer?
If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g the same?
a)
1/25
b)
1/5
c)
1
d)
5
|
|
Suresh Reddy answered |
Since density = M/V and M = gr^2/G and V = 4/3πr^3
Therefore density = (3/4) * (g/πrG) and new density = (3/4)*(g/πr'G)
As r’ = 5r then the new density = ¾ * (g/5rGπ)
d’ = 1/5*3/4(g/πrG)
d'=1/5 d
Therefore density = (3/4) * (g/πrG) and new density = (3/4)*(g/πr'G)
As r’ = 5r then the new density = ¾ * (g/5rGπ)
d’ = 1/5*3/4(g/πrG)
d'=1/5 d
Chapter doubts & questions for Gravitation - NCERT Based Tests for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Gravitation - NCERT Based Tests for NEET in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NCERT Based Tests for NEET
684 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup