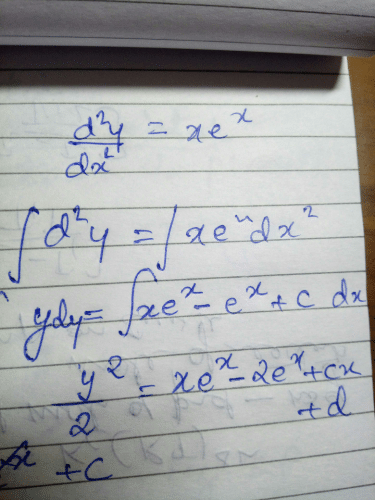All Exams >
JEE >
Mathematics CUET UG Mock Test Series 2026 >
All Questions
All questions of Chapter 9 - Differential Equations for JEE Exam
Low Haemoglobin causes________.
- a)Malaria
- b)Anaemia
- c)Cancer
- d)Cholera
Correct answer is option 'B'. Can you explain this answer?
Low Haemoglobin causes________.
a)
Malaria
b)
Anaemia
c)
Cancer
d)
Cholera
|
|
Priyanka Sharma answered |
Hemoglobin, the substance that gives color to red blood cells, is the substance that allows for the transport of oxygen throughout the body. Low hemoglobin levels lead to anemia, which causes symptoms like fatigue and trouble breathing.
The solution of the initial value problem edy/dx = x + 1, y(0) = 3 is :
- a)y = (x – 1)log(x + 1) + 3
- b)y = (x + 1)log(x + 1) -x+3
- c)y = (x + 1)log(x + 1) + 4
- d)y = (x + 1)log(x + 1) – 1
Correct answer is option 'B'. Can you explain this answer?
The solution of the initial value problem edy/dx = x + 1, y(0) = 3 is :
a)
y = (x – 1)log(x + 1) + 3
b)
y = (x + 1)log(x + 1) -x+3
c)
y = (x + 1)log(x + 1) + 4
d)
y = (x + 1)log(x + 1) – 1

|
Gunjan Lakhani answered |
edy/dx = x + 1
⇒ dy/dx = log(x+1)
⇒ dy = log(x+1)dx
Integrating both sides, we get
⇒ ∫dy = ∫log(x+1)dx
y = log(x + 1) ∫1dx - ∫[d/dx{log(x + 1)} ∫1dx]dx
y = xlog(x + 1) - ∫1/(x+1)xdx
y = xlog(x + 1) - ∫(1 - 1/(x + 1)dx
y = xlog(x + 1) - ∫dx + ∫1/(x+1)dx
y = xlog(x + 1) - x + log|x + 1| + c
y = (x + 1)log|x + 1| - x + c
Here c is 3
y = (x + 1)log|x + 1| - x + 3
⇒ dy/dx = log(x+1)
⇒ dy = log(x+1)dx
Integrating both sides, we get
⇒ ∫dy = ∫log(x+1)dx
y = log(x + 1) ∫1dx - ∫[d/dx{log(x + 1)} ∫1dx]dx
y = xlog(x + 1) - ∫1/(x+1)xdx
y = xlog(x + 1) - ∫(1 - 1/(x + 1)dx
y = xlog(x + 1) - ∫dx + ∫1/(x+1)dx
y = xlog(x + 1) - x + log|x + 1| + c
y = (x + 1)log|x + 1| - x + c
Here c is 3
y = (x + 1)log|x + 1| - x + 3
The differential equation,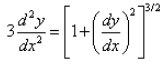 is a:
is a:
- a)second order, third degree equation.
- b)second order, second degree equation.
- c)third order, third degree equation.
- d)second order, first degree equation
Correct answer is option 'D'. Can you explain this answer?
The differential equation,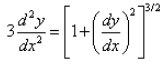 is a:
is a:
a)
second order, third degree equation.
b)
second order, second degree equation.
c)
third order, third degree equation.
d)
second order, first degree equation

|
Divey Sethi answered |
To calculate the degree or the order of a differential equation, the powers of derivatives should be an integer.
On squaring both sides, we get a differential equation with the integral power of derivatives.
On squaring both sides, we get a differential equation with the integral power of derivatives.
⇒ Order (the highest derivative) = 2
⇒ Degree (the power of highest degree) = 1
⇒ Degree (the power of highest degree) = 1
The differential equation 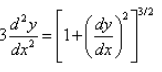 is a:
is a:- a)Third order, third degree equation
- b)Second order, second degree equation
- c)Second order, first degree equation
- d)Second order, third degree equation
Correct answer is option 'B'. Can you explain this answer?
The differential equation 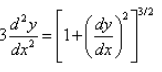 is a:
is a:
a)
Third order, third degree equation
b)
Second order, second degree equation
c)
Second order, first degree equation
d)
Second order, third degree equation
|
|
Suresh Iyer answered |
3*(d2y/dx2) = [1+(dy/dx)2]3/2
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
The differential equation for the equation 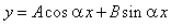 is :
is :- a)
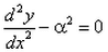
- b)
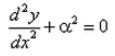
- c)
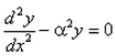
- d)
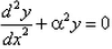
Correct answer is option 'D'. Can you explain this answer?
The differential equation for the equation 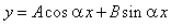 is :
is :
a)
b)
c)
d)

|
Sushil Kumar answered |
y = Acos(αx) + Bsin(αx)
dy/dx = -Aαsin(αx) + Bαcos(αx)
d2y/dx2 = -Aα2cos(αx) - Bα2sin(αx)
= -α2(Acos(αx) + Bsin(αx))
= -α2 * y
d2y/dx2 + α2*y = 0
Differential equation representing the family of curves given by y = ax + x2 is:- a)
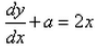
- b)
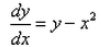
- c)
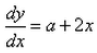
- d)
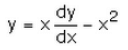
Correct answer is option 'C'. Can you explain this answer?
Differential equation representing the family of curves given by y = ax + x2 is:
a)
b)
c)
d)
|
|
Vikas Kapoor answered |
The answer is C. We eliminate constants.
We have
y=ax+x2
Differentiating with respect to x,
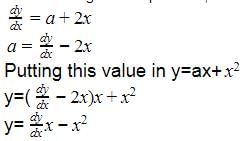
The degree of the differential equation 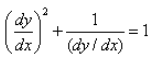
- a)2
- b)1
- c)3
- d)0
Correct answer is option 'C'. Can you explain this answer?
The degree of the differential equation 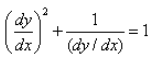
a)
2
b)
1
c)
3
d)
0

|
Sushil Kumar answered |
Given equation is :
(dy/dx)2 + 1/(dy/dx) = 1
((dy/dx)3 + 1)/(dy/dx) = 1
(dy/dx)3 +1 = dy/dx
So, final equation is
(dy/dx)3 - dy/dx + 1 = 0
So, degree = 3
The solution of the differential equation 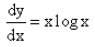 is :
is :- a)2y = x2(log x + 1) + c
- b)
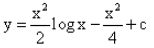
- c)
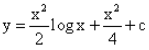
- d)y = x2(log x + 1) + c
Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation 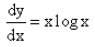 is :
is :
a)
2y = x2(log x + 1) + c
b)
c)
d)
y = x2(log x + 1) + c
|
|
Poonam Reddy answered |
dy/dx = x logx
=> ∫dy = ∫x logx dx
y = logx . x2/2 - ∫1/x . x2/2 dx + c
y = x2/2 log x -½ ∫x dx + c
y = x2/2 log x - ½ . x2/2 + c
y = x2/2 log x - x2/4 + c
=> ∫dy = ∫x logx dx
y = logx . x2/2 - ∫1/x . x2/2 dx + c
y = x2/2 log x -½ ∫x dx + c
y = x2/2 log x - ½ . x2/2 + c
y = x2/2 log x - x2/4 + c
The solution of the differential equation x dy = (2y + 2x4 + x2) dx is:- a)y = x4 + x2 log |x2 + cx2
- b)y = x3 + 2x + cx2
- c)y = x3 + x log |x| + cx
- d)y = x4 + x2 log |x| + cx2
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation x dy = (2y + 2x4 + x2) dx is:
a)
y = x4 + x2 log |x2 + cx2
b)
y = x3 + 2x + cx2
c)
y = x3 + x log |x| + cx
d)
y = x4 + x2 log |x| + cx2

|
Sai Kulkarni answered |
xdy = (2y + 2x4 + x2)dx
→ dy/dx − (2x)y = 2x3 + x
This differential is of the form y′+P(x)y=Q(x) which is the general first order linear differential equation, where P(x) and Q(x) are continuous function defined on an interval.
The general solution for this is y∙I.F = ∫I.F × Q(x)dx
Where I.F = e∫P(x)dx is the integrating factor of the differential equation.
I.F = e∫P(x)dx
= e∫−2/xdx
= e(−2∙lnx)
= eln(x−2)
= x−2
Thus y(1/x2) = ∫1/x2(2x3 + x)dx
=∫(2x + 1/x)dx
= x2 + lnx + C
⟹ y = x4 + x2lnx + c
→ dy/dx − (2x)y = 2x3 + x
This differential is of the form y′+P(x)y=Q(x) which is the general first order linear differential equation, where P(x) and Q(x) are continuous function defined on an interval.
The general solution for this is y∙I.F = ∫I.F × Q(x)dx
Where I.F = e∫P(x)dx is the integrating factor of the differential equation.
I.F = e∫P(x)dx
= e∫−2/xdx
= e(−2∙lnx)
= eln(x−2)
= x−2
Thus y(1/x2) = ∫1/x2(2x3 + x)dx
=∫(2x + 1/x)dx
= x2 + lnx + C
⟹ y = x4 + x2lnx + c
The integrating factor of differential equation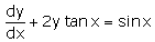 is :
is :- a)-tan x
- b)sec2x
- c)-sec2x
- d)tan x
Correct answer is option 'B'. Can you explain this answer?
The integrating factor of differential equation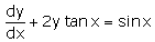 is :
is :
a)
-tan x
b)
sec2x
c)
-sec2x
d)
tan x
|
|
Vikas Kapoor answered |
dy/dx+2ytanx=sinx
This is in the form of dy/dx + py = θ
where p=2tanx,θ=sinx
∴ finding If e∫pdx = e∫2tanxdx
=e(2log secx)
=e(log sec2x)
=sec2x
This is in the form of dy/dx + py = θ
where p=2tanx,θ=sinx
∴ finding If e∫pdx = e∫2tanxdx
=e(2log secx)
=e(log sec2x)
=sec2x
The number of arbitrary constants in the particular solution of a differential equation of third order are:- a)2
- b)0
- c)3
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of arbitrary constants in the particular solution of a differential equation of third order are:
a)
2
b)
0
c)
3
d)
1

|
Akshay Sharma answered |
0 , because the particular solution is free from arbitrary constants.
Order of a differential equation is defined as- a)the number of constant terms
- b)the order of the lowest order derivative ofthe dependent variable
- c)the order of the highest order derivative ofthe dependent variable
- d)the number of derivative terms
Correct answer is option 'C'. Can you explain this answer?
Order of a differential equation is defined as
a)
the number of constant terms
b)
the order of the lowest order derivative ofthe dependent variable
c)
the order of the highest order derivative ofthe dependent variable
d)
the number of derivative terms

|
Sagarika Ahuja answered |
Order of a differential equation is defined asthe order of the highest order derivative ofthe dependent variable.
The solution of the differential equation 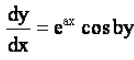 is :
is :
- a)a log sec by + beax = c
- b)a log (sec by + tan by) = beax + c
- c)a log (sec by + tan by) + beax = c
- d)a log sec by + beax + c
Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation 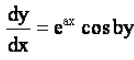 is :
is :
a)
a log sec by + beax = c
b)
a log (sec by + tan by) = beax + c
c)
a log (sec by + tan by) + beax = c
d)
a log sec by + beax + c
|
|
Aryan Khanna answered |
dy/dx = eax cos by
∫dy/cos by = ∫eax dx
∫sec by dy = ∫eax dx
= (log| sec by + tan by|)/b = eax /a + c
= a(log| sec by + tan by|) = beax + c
∫dy/cos by = ∫eax dx
∫sec by dy = ∫eax dx
= (log| sec by + tan by|)/b = eax /a + c
= a(log| sec by + tan by|) = beax + c
The solution of the differential equation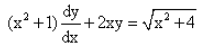 is :
is :- a)
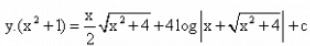
- b)
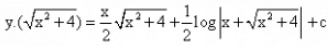
- c)
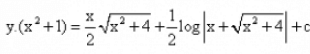
- d)
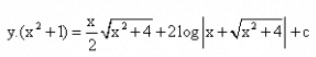
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation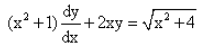 is :
is :
a)
b)
c)
d)

|
Sushil Kumar answered |
The given differential equation may be written as
dy/dx + (2x/(x2+1)y = √x2+4/(x2+1) ... (i)
This is of the form dy/dx + Py = Q,
where P=2x/(x2+1) and Q=(√x2+4)/(x2+1)
Thus, the given differential equation is linear.
IF=e(∫Pdx)
= e(∫2x(x2+1)dx)
= e(log(x2+1) = (x2+1)
So, the required solution is given by
y × IF = ∫{Q×IF}dx + C,
i.e., y(x2+1)=∫(√x2+4)/(x2+1)×(x2+1)dx
⇒y(x2+1)=∫(√x2+4)dx
=1/2x (√x2+4) +1/2 × (2)2 × log|x+(√x2+4)| + C
=1/2x (√x2+4) + 2log|x+(√x2+4) + C.
Hence, y(x2+1) = 1/2x(√x2+4) + 2log|x+√x2+4| + C is the required solution.
dy/dx + (2x/(x2+1)y = √x2+4/(x2+1) ... (i)
This is of the form dy/dx + Py = Q,
where P=2x/(x2+1) and Q=(√x2+4)/(x2+1)
Thus, the given differential equation is linear.
IF=e(∫Pdx)
= e(∫2x(x2+1)dx)
= e(log(x2+1) = (x2+1)
So, the required solution is given by
y × IF = ∫{Q×IF}dx + C,
i.e., y(x2+1)=∫(√x2+4)/(x2+1)×(x2+1)dx
⇒y(x2+1)=∫(√x2+4)dx
=1/2x (√x2+4) +1/2 × (2)2 × log|x+(√x2+4)| + C
=1/2x (√x2+4) + 2log|x+(√x2+4) + C.
Hence, y(x2+1) = 1/2x(√x2+4) + 2log|x+√x2+4| + C is the required solution.
The solution of the differential equation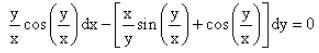 is :
is :- a)
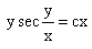
- b)
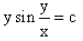
- c)
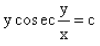
- d)
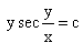
Correct answer is option 'B'. Can you explain this answer?
The solution of the differential equation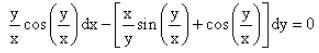 is :
is :
a)
b)
c)
d)
|
|
Aryan Khanna answered |
y/x cos y/x dx − (x/y sin y/x + cosy/x) dy = 0
⇒dy/dx = (y/x cos y/x)/(x/y sin y/x + cos y/x)
This is a homogeneous differential equation.
Putting y = vx and dy/dx = v+xdv/dx, we have v+xdv/dx = (v2cosv)/(sinv+vcosv)
⇒ xdv/dx = (v2cosv)/(sinv+vcosv) - v
⇒x dv/dx = (v2 cosv - v2 cosv - vsinv )/(sinv+vcosv)
⇒ x dv/dx = - [v sinv/(sinv + vcosv)]
⇒ ∫[(sinv + vcosv)/v sinv]dv = ∫dx/x
Integrating both the sides, we get
∫(cot v + 1/v)dv = - ln(x) + c
ln(sin v) + ln(v) = -ln(x) + c
ln(sin(y/x) + ln(y/x) + ln(x) = c
ln(y/x sin y/x * x) + c
y sin(y/x) = c
⇒dy/dx = (y/x cos y/x)/(x/y sin y/x + cos y/x)
This is a homogeneous differential equation.
Putting y = vx and dy/dx = v+xdv/dx, we have v+xdv/dx = (v2cosv)/(sinv+vcosv)
⇒ xdv/dx = (v2cosv)/(sinv+vcosv) - v
⇒x dv/dx = (v2 cosv - v2 cosv - vsinv )/(sinv+vcosv)
⇒ x dv/dx = - [v sinv/(sinv + vcosv)]
⇒ ∫[(sinv + vcosv)/v sinv]dv = ∫dx/x
Integrating both the sides, we get
∫(cot v + 1/v)dv = - ln(x) + c
ln(sin v) + ln(v) = -ln(x) + c
ln(sin(y/x) + ln(y/x) + ln(x) = c
ln(y/x sin y/x * x) + c
y sin(y/x) = c
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :- a)
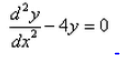
- b)
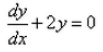
- c)
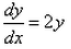
- d)
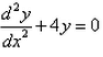
Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :
a)
b)
c)
d)
|
|
Toushit Lohani answered |
Diiferentiate the eqn twice
y' =2(Ae^2x-Be^2x)
y''=4(Ae^2x+Be^2x)
we get
y''-4y=0
Identify the type of differential equation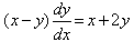
- a)Variable separable
- b)Homogeneous
- c)Linear
- d)Both Variable separable and Linear
Correct answer is option 'B'. Can you explain this answer?
Identify the type of differential equation
a)
Variable separable
b)
Homogeneous
c)
Linear
d)
Both Variable separable and Linear
|
|
Tejas Verma answered |
(x−y)dy/dx = x + 2y
⇒ dy/dx = (x + 2y)/(x−y)
F (x,y) = (x + 2y)/(x−y)
F(Ax, Ay) = (Ax + 2Ay)/(Ax−Ay)
= A(x + 2y)/A(x−y)
= (x + 2y)/(x − y) = F (x,y)
Hence, the equation is homogenous.
⇒ dy/dx = (x + 2y)/(x−y)
F (x,y) = (x + 2y)/(x−y)
F(Ax, Ay) = (Ax + 2Ay)/(Ax−Ay)
= A(x + 2y)/A(x−y)
= (x + 2y)/(x − y) = F (x,y)
Hence, the equation is homogenous.
The order of a differential equation representing a family of curves is same as:- a)The number of arbitrary constants present in the equation.
- b)The number of variables in the equation
- c)The degree of the equation
- d)The number of curves in the family
Correct answer is option 'A'. Can you explain this answer?
The order of a differential equation representing a family of curves is same as:
a)
The number of arbitrary constants present in the equation.
b)
The number of variables in the equation
c)
The degree of the equation
d)
The number of curves in the family
|
|
Palak Datta answered |
The Order of Differential Equations
In the context of differential equations, the order refers to the highest derivative present in the equation. When dealing with a family of curves, the order of the differential equation is closely linked to the number of arbitrary constants it contains.
Understanding Arbitrary Constants
- Arbitrary constants arise when integrating a function, representing a family of solutions or curves.
- For instance, if we have a first-order differential equation, it typically yields one arbitrary constant, leading to a family of curves parameterized by that constant.
Connection to Differential Equations
- The order of the differential equation mirrors the number of arbitrary constants.
- Thus, a second-order differential equation will introduce two arbitrary constants, allowing for a broader family of curves.
Other Options Explained
- Number of Variables: The number of variables in the equation does not directly correlate with the order. A single variable can lead to various orders based on derivatives.
- Degree of the Equation: The degree refers to the power of the highest derivative and is distinct from the order, which is purely about the highest derivative itself.
- Number of Curves in the Family: The number of curves is influenced by the number of arbitrary constants but is not the same as the order.
Conclusion
The correct answer, option 'A', is justified by the direct relationship between the order of a differential equation and the number of arbitrary constants present. This relationship is fundamental in understanding the behavior and characteristics of families of curves represented by differential equations.
In the context of differential equations, the order refers to the highest derivative present in the equation. When dealing with a family of curves, the order of the differential equation is closely linked to the number of arbitrary constants it contains.
Understanding Arbitrary Constants
- Arbitrary constants arise when integrating a function, representing a family of solutions or curves.
- For instance, if we have a first-order differential equation, it typically yields one arbitrary constant, leading to a family of curves parameterized by that constant.
Connection to Differential Equations
- The order of the differential equation mirrors the number of arbitrary constants.
- Thus, a second-order differential equation will introduce two arbitrary constants, allowing for a broader family of curves.
Other Options Explained
- Number of Variables: The number of variables in the equation does not directly correlate with the order. A single variable can lead to various orders based on derivatives.
- Degree of the Equation: The degree refers to the power of the highest derivative and is distinct from the order, which is purely about the highest derivative itself.
- Number of Curves in the Family: The number of curves is influenced by the number of arbitrary constants but is not the same as the order.
Conclusion
The correct answer, option 'A', is justified by the direct relationship between the order of a differential equation and the number of arbitrary constants present. This relationship is fundamental in understanding the behavior and characteristics of families of curves represented by differential equations.
The solution of the differential equation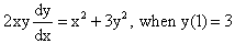 is :
is :- a)x3 + 10y3 = x2
- b)x3 + y3 = 10x2
- c)x3 + y2 = 10x3
- d)x3 -10y3 = x2
Correct answer is option 'C'. Can you explain this answer?
The solution of the differential equation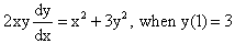 is :
is :
a)
x3 + 10y3 = x2
b)
x3 + y3 = 10x2
c)
x3 + y2 = 10x3
d)
x3 -10y3 = x2
|
|
Om Desai answered |
dy/dx = (x2 + 3y2)/2xy………….(1)
Let y = vx
dy/dx = v + xdv/dx
Substitute the value of y and dy/dx in (1)
v + x dv/dx = (1+3v2)/2v
x dv/dx = (1+3v2)/2v - v
x dv/dx = (1 + 3v2 - 2v2)/2
x dv/dx = (1+ v2)/2v
2v/(1+v2) dv = dx/x…………(2)
Integrating both the sides
∫2v/(1+v2) dv = ∫dx/x
Put t = 1 + v2
dt = 2vdv
∫dt/t = ∫dx/x
=> log|t| = log|x| + log|c|
=> log|t/x| = log|c|
t/x = +- c
(1+v2)/x = +-c
(1 + (y2)/(x2))/x = +-c
x2 + y2 = Cx3……….(3)
y(1) = 3
1 + 9 = c(1)3
c = 10
From eq(3), we get x
Let y = vx
dy/dx = v + xdv/dx
Substitute the value of y and dy/dx in (1)
v + x dv/dx = (1+3v2)/2v
x dv/dx = (1+3v2)/2v - v
x dv/dx = (1 + 3v2 - 2v2)/2
x dv/dx = (1+ v2)/2v
2v/(1+v2) dv = dx/x…………(2)
Integrating both the sides
∫2v/(1+v2) dv = ∫dx/x
Put t = 1 + v2
dt = 2vdv
∫dt/t = ∫dx/x
=> log|t| = log|x| + log|c|
=> log|t/x| = log|c|
t/x = +- c
(1+v2)/x = +-c
(1 + (y2)/(x2))/x = +-c
x2 + y2 = Cx3……….(3)
y(1) = 3
1 + 9 = c(1)3
c = 10
From eq(3), we get x
3
+ y2 = 10x3The solution of the equation x3dx + (y + 1)2 dy = 0- a)12[x4 - (y +1)3] = c
- b)12[x4 + (y +1)3] = c
- c)3x4 + 4(y +1)3 = c
- d)3x4 + 3(y +1)3 = c
Correct answer is option 'C'. Can you explain this answer?
The solution of the equation x3dx + (y + 1)2 dy = 0
a)
12[x4 - (y +1)3] = c
b)
12[x4 + (y +1)3] = c
c)
3x4 + 4(y +1)3 = c
d)
3x4 + 3(y +1)3 = c
|
|
Om Desai answered |
x3dx + (y + 1)dy = 0
=> d(x4/4) + d((y + 1)3/3) = 0
=> d(x4/4 + ((y + 1)3/3)) = 0
=> (x4/4 + ((y + 1)3/3)) = constt
=> 12 *(x4/4 + ((y + 1)3/3)) = 12 * constt
=> 3x4 + 4(y + 1)3 = constt
=> d(x4/4) + d((y + 1)3/3) = 0
=> d(x4/4 + ((y + 1)3/3)) = 0
=> (x4/4 + ((y + 1)3/3)) = constt
=> 12 *(x4/4 + ((y + 1)3/3)) = 12 * constt
=> 3x4 + 4(y + 1)3 = constt
Write the order and degree of the given differential equation: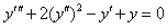
- a)2,3
- b)1,1
- c)2,1
- d)3, 1
Correct answer is option 'D'. Can you explain this answer?
Write the order and degree of the given differential equation:
a)
2,3
b)
1,1
c)
2,1
d)
3, 1
|
|
Gaurav Kumar answered |
Order = 3 and Degree = 1
The order of a differential equation is determined by the highest-order derivative; the degree is determined by the highest power on a variable. The higher the order of the differential equation, the more arbitrary constants need to be added to the general solution.
The order of a differential equation is determined by the highest-order derivative; the degree is determined by the highest power on a variable. The higher the order of the differential equation, the more arbitrary constants need to be added to the general solution.
The first order, first degree differential equation y’ = f(x,y) is said to be homogeneous, if- a)f(x , y) is a homogeneous function of degree zero.
- b)f(x , y) is a homogeneous function of second degree.
- c)f(x , y) is a homogeneous function of first degree.
- d)f(x , y) is a homogeneous function of third degree.
Correct answer is option 'A'. Can you explain this answer?
The first order, first degree differential equation y’ = f(x,y) is said to be homogeneous, if
a)
f(x , y) is a homogeneous function of degree zero.
b)
f(x , y) is a homogeneous function of second degree.
c)
f(x , y) is a homogeneous function of first degree.
d)
f(x , y) is a homogeneous function of third degree.

|
Arshiya Mehta answered |
The correct answer is option A, because a first-order, first-degree differential equation is said to be homogeneous if the function f(x,y) is a homogeneous function of degree zero.
A function f(x,y) is said to be homogeneous of degree n if it satisfies the equation:
f(λx, λy) = λ^n * f(x,y)
where λ is a scalar. This means that if we multiply both the independent and dependent variables by a constant λ, the value of the function is scaled by a factor of λ^n.
In the case of a first-order, first-degree differential equation, the function f(x,y) is a function of two variables: x and y. For this type of equation, f(x,y) is said to be homogeneous if it is a homogeneous function of degree zero, which means that it satisfies the equation:
f(λx, λy) = f(x,y)
In other words, if we multiply both the independent and dependent variables by a constant λ, the value of the function does not change. This means that f(x,y) does not depend on the magnitude of the variables x and y, but only on their relative values.
For example, if f(x,y) = xy, then f(λx, λy) = λxy = xy, so f(x,y) is a homogeneous function of degree zero. On the other hand, if f(x,y) = x^2 + y^2, then f(λx, λy) = λ^2x^2 + λ^2y^2 = x^2 + y^2, so f(x,y) is not a homogeneous function.
Therefore, the correct answer is option A, because a first-order, first-degree differential equation is said to be homogeneous if the function f(x,y) is a homogeneous function of degree zero.
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:- a)
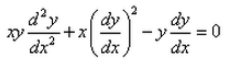
- b)
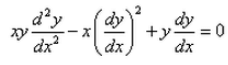
- c)
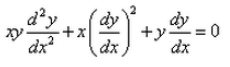
- d)
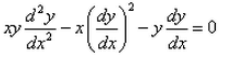
Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:
a)
b)
c)
d)
|
|
Geetika Shah answered |
Equation of ellipse :
x2/a2 + y2/b2 = 1
Differentiation by x,
2x/a2 + (dy/dx)*(2y/b2) = 0
dy/dx = -(b2/a2)(x/y)
-(b2/a^2) = (dy/dx)*(y/x) ----- eqn 1
Again differentiating by x,
d2y/dx2 = -(b2/a2)*((y-x(dy/dx))/y2)
Substituting value of -b2/a2 from eqn 1
d2y/dx2 = (dy/dx)*(y/x)*((y-x(dy/dx))/y2)
d2y/dx2 = (dy/dx)*((y-x*(dy/dx))/xy)
(xy)*(d2y/dx2) = y*(dy/dx) - x*(dy/dx)2
(xy)*(d2y/dx2) + x*(dy/dx)2- y*(dy/dx) = 0
Solution of x dy− ydx = 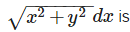
- a)
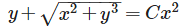
- b)
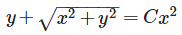
- c)
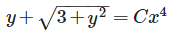
- d)
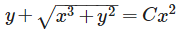
Correct answer is option 'B'. Can you explain this answer?
Solution of x dy− ydx = 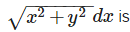
a)
b)
c)
d)
|
|
Harsh Singhal answered |
Solve by put x=rcos$ & y=rsin$
Differential equations are equations containing functions y = f(x), g(x) and- a)tangent of y at zero
- b)maxima of y
- c)derivatives of y
- d)minima of y
Correct answer is option 'C'. Can you explain this answer?
Differential equations are equations containing functions y = f(x), g(x) and
a)
tangent of y at zero
b)
maxima of y
c)
derivatives of y
d)
minima of y
|
|
Dipanjan Verma answered |
Differential equations are mathematical equations that involve derivatives of an unknown function. They are widely used in various fields of science and engineering to model and analyze dynamic systems. In this question, we are asked to identify the correct option regarding the nature of the functions involved in differential equations.
Differential equations involve functions y = f(x) and g(x), where y represents the dependent variable and x represents the independent variable. These functions can have various properties and behaviors based on the given equation. Let's analyze each option to understand why option 'C' is the correct answer.
a) Tangent of y at zero:
The tangent of a function at a specific point represents the slope of the function at that point. This option suggests that the differential equation involves the tangent of y at zero. However, this is not a general characteristic of differential equations. Differential equations can involve tangents at any point, not just zero.
b) Maxima of y:
Maxima of a function refers to the points where the function reaches its highest values. While differential equations can involve maxima or minima, it is not a general property of all differential equations. Therefore, this option is not correct.
c) Derivatives of y:
This option suggests that the differential equations involve derivatives of y. This is the correct answer. Differential equations often involve derivatives of the unknown function y with respect to the independent variable x. By including derivatives, we can describe how the rate of change of y varies with respect to x.
d) Minima of y:
Minima of a function refers to the points where the function reaches its lowest values. Similar to option 'b', this is not a general property of all differential equations. While some differential equations may involve minima, it is not a defining characteristic.
In conclusion, the correct answer is option 'c' because differential equations commonly involve derivatives of the unknown function y. Including derivatives allows us to describe the rate of change and behavior of the function with respect to the independent variable.
Differential equations involve functions y = f(x) and g(x), where y represents the dependent variable and x represents the independent variable. These functions can have various properties and behaviors based on the given equation. Let's analyze each option to understand why option 'C' is the correct answer.
a) Tangent of y at zero:
The tangent of a function at a specific point represents the slope of the function at that point. This option suggests that the differential equation involves the tangent of y at zero. However, this is not a general characteristic of differential equations. Differential equations can involve tangents at any point, not just zero.
b) Maxima of y:
Maxima of a function refers to the points where the function reaches its highest values. While differential equations can involve maxima or minima, it is not a general property of all differential equations. Therefore, this option is not correct.
c) Derivatives of y:
This option suggests that the differential equations involve derivatives of y. This is the correct answer. Differential equations often involve derivatives of the unknown function y with respect to the independent variable x. By including derivatives, we can describe how the rate of change of y varies with respect to x.
d) Minima of y:
Minima of a function refers to the points where the function reaches its lowest values. Similar to option 'b', this is not a general property of all differential equations. While some differential equations may involve minima, it is not a defining characteristic.
In conclusion, the correct answer is option 'c' because differential equations commonly involve derivatives of the unknown function y. Including derivatives allows us to describe the rate of change and behavior of the function with respect to the independent variable.
Degree of a differential equation, when the equation is polynomial equation in y′ is- a)Highest (positive integral index) of the lowest order derivative in the given differential equation.
- b)Lowest power (positive integral index) of the highest order derivative in the given differential equation.
- c)Lowest power (positive integral index) of the lowest order derivative in the given differential equation.
- d)Highest power (positive integral index) of the highest order derivative in the given differential equation.
Correct answer is option 'D'. Can you explain this answer?
Degree of a differential equation, when the equation is polynomial equation in y′ is
a)
Highest (positive integral index) of the lowest order derivative in the given differential equation.
b)
Lowest power (positive integral index) of the highest order derivative in the given differential equation.
c)
Lowest power (positive integral index) of the lowest order derivative in the given differential equation.
d)
Highest power (positive integral index) of the highest order derivative in the given differential equation.
|
|
Malavika Menon answered |
The degree of a differential equation is determined by the highest power of the derivative(s) present in the equation.
When the equation is a polynomial equation in y, the degree is determined by the highest power of y in the equation. The derivative(s) of y do not affect the degree in this case.
When the equation is a polynomial equation in y, the degree is determined by the highest power of y in the equation. The derivative(s) of y do not affect the degree in this case.
Direction: Read the following text and answer the following questions on the basis of the same:Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.Q. The value of C in the particular solution given that y(0) = 0 and k = 0.049 is- a)log 50
- b)log 1/50
- c)50
- d)-50
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. The value of C in the particular solution given that y(0) = 0 and k = 0.049 is
a)
log 50
b)
log 1/50
c)
50
d)
-50
|
|
Ananya Das answered |
Given,
y(0) = and k = 0.049
We have, -log|50 - y| = Kx + C
log |50 - y| = -Kx - C
log |50 - 0| = 0 - C
[∵ x = 0, K = 0.049, y(0) = 0]
log 50 = - C
C = log 1/50
Direction: Read the following text and answer the following questions on the basis of the same:Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.Q. Which method of solving a differential equation can be used to solve dy/dx = k(50 - y)?- a)Variable separable method
- b)Solving Homogeneous differential equation
- c)Solving Linear differential equation
- d)All of the above
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. Which method of solving a differential equation can be used to solve dy/dx = k(50 - y)?
a)
Variable separable method
b)
Solving Homogeneous differential equation
c)
Solving Linear differential equation
d)
All of the above
|
|
Ananya Das answered |
‘Variable separable method’ is used to solve such an equation in which variables
can be separated completely, i.e., terms containing x should remain with dx and terms containing y should remain with dy.
Direction: Read the following text and answer the following questions on the basis of the same:Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.Q. The solution of the differential equation dy/dx = k(50 - y) is given by,- a)log |50 – y| = kx + C
- b)–log |50 – y| = kx + C
- c)log |50 – y| = log|kx|+ C
- d)50 – y = kx + C
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. The solution of the differential equation dy/dx = k(50 - y) is given by,
a)
log |50 – y| = kx + C
b)
–log |50 – y| = kx + C
c)
log |50 – y| = log|kx|+ C
d)
50 – y = kx + C
|
|
Ananya Das answered |
Dy/dx = k(50 - y)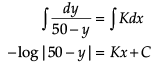
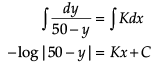
A differential equation of the form y' = F(x,y) is homogeneous if- a)F(x,y) is a homogeneous function of degree one
- b)F(x,y) is a homogeneous function of degree three
- c)F(x,y) is a homogeneous function of degree two
- d)F(x,y) is a homogeneous function of degree zero
Correct answer is option 'D'. Can you explain this answer?
A differential equation of the form y' = F(x,y) is homogeneous if
a)
F(x,y) is a homogeneous function of degree one
b)
F(x,y) is a homogeneous function of degree three
c)
F(x,y) is a homogeneous function of degree two
d)
F(x,y) is a homogeneous function of degree zero

|
Gayatri Patel answered |
A differential equation of the form y' = F(x,y) is homogeneous if F(x,y) is a homogeneous function of degree zero.
Variable separation method can be used to solve First Order, First Degree Differential Equations in which y’ is of the form.- a)y’ = h(x)g(y)
- b)y2 = sin (h(x))
- c)y2 = cos (g(y))
- d)y3 = g(y)
Correct answer is option 'A'. Can you explain this answer?
Variable separation method can be used to solve First Order, First Degree Differential Equations in which y’ is of the form.
a)
y’ = h(x)g(y)
b)
y2 = sin (h(x))
c)
y2 = cos (g(y))
d)
y3 = g(y)

|
Prasenjit Malik answered |
Variable separation method can be used to solveFirst Order, First Degree Differential Equations in which y’ is of the form. y’ = h(x)g(y) i.e 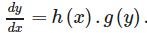
Direction: Read the following text and answer the following questions on the basis of the same:Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.Q. Which of the following solutions may be used to find the number of children who have been given the polio drops?- a)y = 50 – ekx
- b)y = 50 – e–kx
- c)y = 50(1 – e–kx)
- d)y = 50(e–kx – 1)
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Polio drops are delivered to 50K children in a district. The rate at which polio drops are given is directly proportional to the number of children who have not been administered the drops. By the end of 2nd week half the children have been given the polio drops. How many will have been given the drops by the end of 3rd week can be estimated using the solution to the differential equation dy/dx = k(50 - y) where x denotes the number of weeks and y the number of children who have been given the drops.
Q. Which of the following solutions may be used to find the number of children who have been given the polio drops?
a)
y = 50 – ekx
b)
y = 50 – e–kx
c)
y = 50(1 – e–kx)
d)
y = 50(e–kx – 1)
|
|
Ananya Das answered |
We have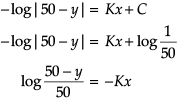
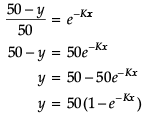
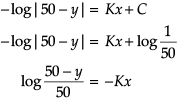
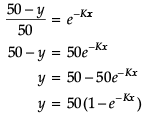
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:- a)2, 4
- b)3, 5
- c)2, 5
- d)2, 3
Correct answer is option 'D'. Can you explain this answer?
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:
a)
2, 4
b)
3, 5
c)
2, 5
d)
2, 3
|
|
Naina Bansal answered |
Toolbox:
The highest order derivative present in the differential equation determines its order.
The highest power raise to the derivative determines its degree.
(y′′′)^2+(y′′)^3+(y′)^4+y^5 = 0
The order of the given equation is 3.
The degree corresponding to the highest order is 2
The order of the differential equation: 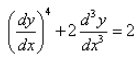
- a)4
- b)2
- c)3
- d)1
Correct answer is option 'C'. Can you explain this answer?
The order of the differential equation: 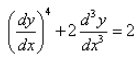
a)
4
b)
2
c)
3
d)
1

|
Anuj Seth answered |
Order is seen from highest efficiency of differentiability I.e. in hindi , kisi bhi equation me jisme sabse jyada differential power hai wo jeeta
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).- a)7.93%
- b)8.93%
- c)9.93%
- d)6.93%
Correct answer is option 'D'. Can you explain this answer?
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
a)
7.93%
b)
8.93%
c)
9.93%
d)
6.93%
|
|
Anirban Desai answered |
To solve this problem, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial amount)
r is the annual interest rate (as a decimal)
n is the number of times the interest is compounded per year
t is the number of years
In this case, the principal doubles itself in 10 years. So, the final amount A is 2 times the principal P.
2P = P(1 + r/n)^(nt)
Since we are given that the principal increases continuously, we can take the limit as n approaches infinity. This simplifies the formula to:
2 = e^(rt)
Where e is the base of natural logarithms and is approximately equal to 2.71828.
Now, we can take the natural logarithm of both sides to solve for r:
ln(2) = rt
Dividing both sides by t:
r = ln(2)/t
Given that t = 10 years, we can substitute this value into the equation:
r = ln(2)/10
Using the given value of loge2 = 0.6931, we can calculate r:
r = 0.6931/10 = 0.06931 = 6.93%
Therefore, the value of r is 6.93%.
So, the correct answer is option D.
A = P(1 + r/n)^(nt)
Where:
A is the final amount
P is the principal amount (initial amount)
r is the annual interest rate (as a decimal)
n is the number of times the interest is compounded per year
t is the number of years
In this case, the principal doubles itself in 10 years. So, the final amount A is 2 times the principal P.
2P = P(1 + r/n)^(nt)
Since we are given that the principal increases continuously, we can take the limit as n approaches infinity. This simplifies the formula to:
2 = e^(rt)
Where e is the base of natural logarithms and is approximately equal to 2.71828.
Now, we can take the natural logarithm of both sides to solve for r:
ln(2) = rt
Dividing both sides by t:
r = ln(2)/t
Given that t = 10 years, we can substitute this value into the equation:
r = ln(2)/10
Using the given value of loge2 = 0.6931, we can calculate r:
r = 0.6931/10 = 0.06931 = 6.93%
Therefore, the value of r is 6.93%.
So, the correct answer is option D.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).- a)(x + 3)2 = y + 4
- b)(x + 5)2 = 2y + 3
- c)(x + 4)2 = y + 3
- d)(x + 5)2 = 2y + 3
Correct answer is option 'C'. Can you explain this answer?
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).
a)
(x + 3)2 = y + 4
b)
(x + 5)2 = 2y + 3
c)
(x + 4)2 = y + 3
d)
(x + 5)2 = 2y + 3
|
|
Rounak Verma answered |
Understanding the Problem
- We need to find a curve where the slope of the tangent at any point (x, y) is twice the slope of the line segment connecting (x, y) to the fixed point (4, 3).
- The curve also passes through the point (2, 1).
Finding the Slopes
- The slope of the tangent at point (x, y) is represented as dy/dx.
- The slope of the line segment from (x, y) to (4, 3) is calculated as (3 - y) / (4 - x).
Setting Up the Equation
- According to the problem, we have:
dy/dx = 2 * ((3 - y) / (4 - x))
Rearranging the Equation
- Rearranging the equation gives:
dy/dx = (2(3 - y)) / (4 - x)
Separation of Variables
- To solve this differential equation, we can rearrange the terms:
(4 - x) dy = 2(3 - y) dx
Integrating Both Sides
- Integrate both sides to find the equation of the curve:
∫(4 - x) dy = ∫2(3 - y) dx
- This results in:
y(4-x) = 6x - x^2 + C
Using Initial Condition
- With the condition that the curve passes through (2, 1), substitute these values to find C:
1(4-2) = 6(2) - (2^2) + C
2 = 12 - 4 + C
C = -6
Final Equation of the Curve
- Substitute C back into the equation:
y(4 - x) = 6x - x^2 - 6
- Rearranging gives the form:
(x + 4)² = y + 3
- Thus, the equation of the curve is:
(x + 4)² = y + 3, which corresponds to option C.
- We need to find a curve where the slope of the tangent at any point (x, y) is twice the slope of the line segment connecting (x, y) to the fixed point (4, 3).
- The curve also passes through the point (2, 1).
Finding the Slopes
- The slope of the tangent at point (x, y) is represented as dy/dx.
- The slope of the line segment from (x, y) to (4, 3) is calculated as (3 - y) / (4 - x).
Setting Up the Equation
- According to the problem, we have:
dy/dx = 2 * ((3 - y) / (4 - x))
Rearranging the Equation
- Rearranging the equation gives:
dy/dx = (2(3 - y)) / (4 - x)
Separation of Variables
- To solve this differential equation, we can rearrange the terms:
(4 - x) dy = 2(3 - y) dx
Integrating Both Sides
- Integrate both sides to find the equation of the curve:
∫(4 - x) dy = ∫2(3 - y) dx
- This results in:
y(4-x) = 6x - x^2 + C
Using Initial Condition
- With the condition that the curve passes through (2, 1), substitute these values to find C:
1(4-2) = 6(2) - (2^2) + C
2 = 12 - 4 + C
C = -6
Final Equation of the Curve
- Substitute C back into the equation:
y(4 - x) = 6x - x^2 - 6
- Rearranging gives the form:
(x + 4)² = y + 3
- Thus, the equation of the curve is:
(x + 4)² = y + 3, which corresponds to option C.
Differential equation of the family of ellipses having foci on y-axis and centre at origin is- a)xy′′ + x(y′)2 yy′ = 0
- b)xyy′′ + x(y′)2 yy′ = 0
- c)yy′′ + x(y′)2 yy′ = 0
- d)xyy′′ −x(y′)2 +yy′ = 0
Correct answer is option 'B'. Can you explain this answer?
Differential equation of the family of ellipses having foci on y-axis and centre at origin is
a)
xy′′ + x(y′)2 yy′ = 0
b)
xyy′′ + x(y′)2 yy′ = 0
c)
yy′′ + x(y′)2 yy′ = 0
d)
xyy′′ −x(y′)2 +yy′ = 0
|
|
Palak Banerjee answered |
The differential equation of the family of ellipses having foci on the y-axis and center at the origin can be found as follows:
Let's consider an ellipse with foci (0, c) and (0, -c), where c is a positive constant. The distance between the foci is 2c.
The general equation of an ellipse centered at the origin is given by:
x^2/a^2 + y^2/b^2 = 1,
where a and b are positive constants representing the semi-major and semi-minor axes, respectively.
Since the foci lie on the y-axis, the equation of the ellipse becomes:
x^2/a^2 + (y - c)^2/b^2 = 1.
We know that the distance between the foci is 2c, so we have:
2c = 2b^2/a.
Simplifying this equation, we get:
b^2 = ac.
Now, differentiating both sides of the equation with respect to x, we have:
2b(b') = a'c + ac',
where b' and a' represent the derivatives of b and a with respect to x, respectively.
Since the derivatives of a and b are unknown, we cannot solve for the differential equation in terms of x and y directly. However, we can eliminate a' and b' by using the relationship b^2 = ac, which gives:
2b(b') = 2b(c'/b) + ac'.
Simplifying this equation, we find:
b' = c'/b + ac'/(2b^2).
Rearranging terms, we get:
b'(2b^2) = c' + ac'.
Substituting b^2 = ac, we obtain:
b'(2b^2) = c' + b^2c'.
Finally, dividing both sides by 2b^2, we get the differential equation:
b' = (c' + b^2c')/(2b^2).
Therefore, the differential equation of the family of ellipses having foci on the y-axis and center at the origin is:
b' = (c' + b^2c')/(2b^2).
Let's consider an ellipse with foci (0, c) and (0, -c), where c is a positive constant. The distance between the foci is 2c.
The general equation of an ellipse centered at the origin is given by:
x^2/a^2 + y^2/b^2 = 1,
where a and b are positive constants representing the semi-major and semi-minor axes, respectively.
Since the foci lie on the y-axis, the equation of the ellipse becomes:
x^2/a^2 + (y - c)^2/b^2 = 1.
We know that the distance between the foci is 2c, so we have:
2c = 2b^2/a.
Simplifying this equation, we get:
b^2 = ac.
Now, differentiating both sides of the equation with respect to x, we have:
2b(b') = a'c + ac',
where b' and a' represent the derivatives of b and a with respect to x, respectively.
Since the derivatives of a and b are unknown, we cannot solve for the differential equation in terms of x and y directly. However, we can eliminate a' and b' by using the relationship b^2 = ac, which gives:
2b(b') = 2b(c'/b) + ac'.
Simplifying this equation, we find:
b' = c'/b + ac'/(2b^2).
Rearranging terms, we get:
b'(2b^2) = c' + ac'.
Substituting b^2 = ac, we obtain:
b'(2b^2) = c' + b^2c'.
Finally, dividing both sides by 2b^2, we get the differential equation:
b' = (c' + b^2c')/(2b^2).
Therefore, the differential equation of the family of ellipses having foci on the y-axis and center at the origin is:
b' = (c' + b^2c')/(2b^2).
The solution of the differential equation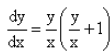 is :
is :- a)
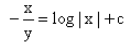
- b)
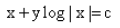
- c)
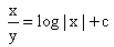
- d)
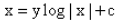
Correct answer is option 'A'. Can you explain this answer?
The solution of the differential equation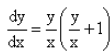 is :
is :
a)
b)
c)
d)

|
Peter Parker answered |
Option A is correct...
Chapter doubts & questions for Chapter 9 - Differential Equations - Mathematics CUET UG Mock Test Series 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 9 - Differential Equations - Mathematics CUET UG Mock Test Series 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily