All Exams >
JAMB >
Physics for JAMB >
All Questions
All questions of Equilibrium of Forces for JAMB Exam
The centre of mass of a body is locateda)outside the systemb)inside or outside the systemc)inside the systemd)at the centre of systemCorrect answer is option 'B'. Can you explain this answer?
|
|
Suresh Iyer answered |
The centre of mass of a body can lie within or outside the body.
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Can you explain the answer of this question below:Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
- A:
10 m/s
- B:
5 m/s
- C:
15 m/s
- D:
20 m/s
The answer is a.
Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
10 m/s
5 m/s
15 m/s
20 m/s

|
EduRev JEE answered |
Velocity of heavier block (v2) = 14m/s
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,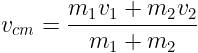
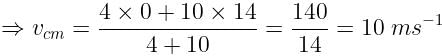
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,
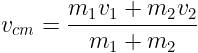
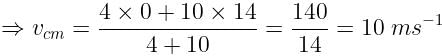
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
- a)Is zero
- b)Remains constant
- c)Goes on increasing
- d)Goes on decreasing
Correct answer is option 'B'. Can you explain this answer?
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
a)
Is zero
b)
Remains constant
c)
Goes on increasing
d)
Goes on decreasing
|
|
Krishna Iyer answered |
Angular momentum (L) is defined as the distance of the object from a rotation axis multiplied by the linear momentum
L = mv×y
L = mv×y
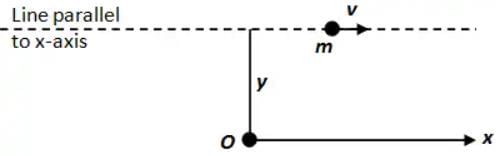
As the particle moves, m; v; and y, all remain unchanged at any point of time
⇒ L = constant
⇒ L = constant
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are- a)( 2, -1 )
- b)( 8/3 ,-1/3 )
- c)( -1/3 , 8/3 )
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are
a)
( 2, -1 )
b)
( 8/3 ,-1/3 )
c)
( -1/3 , 8/3 )
d)
none of these
|
|
Riya Banerjee answered |
Body A has mass of 1kg and location (1,2)
Body B has mass of 2kg and location (-1,3)
Body B has mass of 2kg and location (-1,3)
mcxc = m1x1 + m2x2
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
Similarly,
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
Hence, the coordinates of the center of mass are (-1/3, 8/3).
The motion of a potter’s wheel is an example of
- a)rolling motion
- b)rotatory motion
- c)translatory motion
- d)precessional motion
Correct answer is option 'B'. Can you explain this answer?
The motion of a potter’s wheel is an example of
a)
rolling motion
b)
rotatory motion
c)
translatory motion
d)
precessional motion
|
|
Anjali Iyer answered |
Potter’s wheel is an example of rotary motion. Rotary motion is that kind of motion in which body of the mass moves along a circular path about an axis which remains fixed.
The centre of mass of a system of particles does not depend on
- a)masses of the particles
- b)forces on the particles
- c)relative distances between the particles
- d)position of the particles
Correct answer is option 'B'. Can you explain this answer?
The centre of mass of a system of particles does not depend on
a)
masses of the particles
b)
forces on the particles
c)
relative distances between the particles
d)
position of the particles
|
|
Neha Joshi answered |
The resultant of all forces, on any system of particles, is zero. Therefore, their centre of mass does not depend upon the forces acting on the particles.
An engine develops a power of 360 kw, when rotating at 30 revolutions per second. The Torque required to deliver this power is- a)191.08 Nm
- b)19108 Nm
- c)1910.8 Nm
- d)19.108 Nm
Correct answer is option 'C'. Can you explain this answer?
An engine develops a power of 360 kw, when rotating at 30 revolutions per second. The Torque required to deliver this power is
a)
191.08 Nm
b)
19108 Nm
c)
1910.8 Nm
d)
19.108 Nm
|
|
Preeti Iyer answered |
The power delivered by the torque τ exerted on rotating body is given by
P=τω or τ=P/ω
Here P=360KW=360000 Watt
ω=30 x 2π rad/sec,
ω=60π rad/sec
now,
τ=360000 /60×3.14Nm
τ= 1910.8 Nm
P=τω or τ=P/ω
Here P=360KW=360000 Watt
ω=30 x 2π rad/sec,
ω=60π rad/sec
now,
τ=360000 /60×3.14Nm
τ= 1910.8 Nm
If a shell at rest explodes then the centre of mass of the fragments
- a)remains at rest
- b)Moves along a parabolic path
- c)Moves along a straight line
- d)moves along an elliptical path
Correct answer is option 'A'. Can you explain this answer?
If a shell at rest explodes then the centre of mass of the fragments
a)
remains at rest
b)
Moves along a parabolic path
c)
Moves along a straight line
d)
moves along an elliptical path
|
|
Gaurav Kumar answered |
As a shell explosion is not governed by any external force, we get that no external force acts upon the shell, and hence it remains at rest.
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)- a)
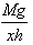
- b)
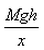
- c)
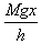
- d)
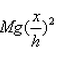
Correct answer is option 'B'. Can you explain this answer?
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)
a)
b)
c)
d)
|
|
Neha Joshi answered |
As the center of mass moves through a distance x, the average force F acting on the man is calculated from :
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =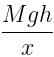
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =
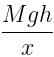
When external forces acting on a body are zero, then its centre of mass- a)remains stationary
- b)moves with uniform velocity
- c)either remains stationary or moves with uniform velocity
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
When external forces acting on a body are zero, then its centre of mass
a)
remains stationary
b)
moves with uniform velocity
c)
either remains stationary or moves with uniform velocity
d)
none of these
|
|
Naina Sharma answered |
When force acting upon the body results zero, the resulting acceleration due to net force applied is also zero, and hence by the law of inertia the motion of the body either at rest or constant velocity wont change.
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
- a)both C1 and C2 will move with respect to the ground
- b)neither C1 nor C2 will move with respect to the ground
- c)C1 will move but C2 will be stationary with respect to the ground
- d)C2 will move but C1 will be stationary with respect to the ground
Correct answer is option 'C'. Can you explain this answer?
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
a)
both C1 and C2 will move with respect to the ground
b)
neither C1 nor C2 will move with respect to the ground
c)
C1 will move but C2 will be stationary with respect to the ground
d)
C2 will move but C1 will be stationary with respect to the ground
|
|
Lavanya Menon answered |
When net Fexternal=0, then the centre of mass of the system remains at rest.
Thus if the passenger move inside the compartment which donot require any external force, so the centre of mass of the "passenger + compartment" system must remain at rest and hence C2 will be fixed w.r.t ground.
Also due to the movement of the passenger, the position of centre of mass of the passengers only will change, thus C1 will have to move in such a way that C2 may remain fixed w.r.t ground.
Moment of inertia of a solid sphere of mass M and radius R is ______- a)MR2
- b)2/5MR2
- c)2/3MR2
- d)1/2MR2
Correct answer is option 'B'. Can you explain this answer?
Moment of inertia of a solid sphere of mass M and radius R is ______
a)
MR2
b)
2/5MR2
c)
2/3MR2
d)
1/2MR2
|
|
Sarita Pandey answered |
Moment of inertia of a solid sphere of mass M and radius R = 2/5 MR^2
A rigid body is one
- a)the sum of distances of all particles from the axis remains constant
- b)in which the distance between all pairs of particles remains fixed
- c)whose centre of mass follows a parabolic path
- d)that deforms and comes back to its original shape after getting deformed
Correct answer is option 'B'. Can you explain this answer?
A rigid body is one
a)
the sum of distances of all particles from the axis remains constant
b)
in which the distance between all pairs of particles remains fixed
c)
whose centre of mass follows a parabolic path
d)
that deforms and comes back to its original shape after getting deformed
|
|
Krishna Iyer answered |
A body is said to be a rigid body if the body remains in its original shape even under the influence of external force. We can also say that if distance between two points of the body does not change with time regardless of external forces exerted on it, then the body is said to be a rigid body.
Two spheres of masses m1 and m2 (m1>m2) respectively are tied to the ends of a light, inextensible string which passes over a light frictionless pulley. When the masses are released from their initial state of rest, the acceleration of their centre of mass is: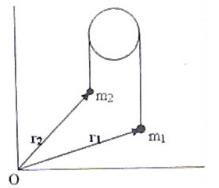
- a)
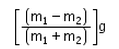
- b)
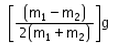
- c)
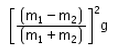
- d)
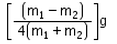
Correct answer is option 'C'. Can you explain this answer?
Two spheres of masses m1 and m2 (m1>m2) respectively are tied to the ends of a light, inextensible string which passes over a light frictionless pulley. When the masses are released from their initial state of rest, the acceleration of their centre of mass is:
a)
b)
c)
d)

|
Sushil Kumar answered |
If, r1 and r2 are position vectors of the centres of the positional vector of their centre of mass is given by R=(m1r1+m2r2)/ (m1 + m2)
R= (m1r2+m2r2)/m1+m2)
The acceleration of the centre of mass is given by:
A=d2R/dt
= [m1 d2r/dt+m2 d2r/dt2 ]/(m1+m2)
But, d2r1/dt2 and d2r2/dt2 are the accelerations of masses m1 and m2
Have the same magnitude (m1-m2)/(m1+m2) g
If we take acceleration of [m1(m1-m2)/ (m1+m2)g – m2(m1-m2)/ (m1+m2)/]/ (m1+m2)
On simplifying that we get,
a=[(m1-m2)/ (m1+m2)]2 g
R= (m1r2+m2r2)/m1+m2)
The acceleration of the centre of mass is given by:
A=d2R/dt
= [m1 d2r/dt+m2 d2r/dt2 ]/(m1+m2)
But, d2r1/dt2 and d2r2/dt2 are the accelerations of masses m1 and m2
Have the same magnitude (m1-m2)/(m1+m2) g
If we take acceleration of [m1(m1-m2)/ (m1+m2)g – m2(m1-m2)/ (m1+m2)/]/ (m1+m2)
On simplifying that we get,
a=[(m1-m2)/ (m1+m2)]2 g
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?- a)At the point of intersection of the medians.
- b)At the line joining the centers of any two balls.
- c)At the centre of one of the ball.
- d)At the horizontal surface.
Correct answer is option 'A'. Can you explain this answer?
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?
a)
At the point of intersection of the medians.
b)
At the line joining the centers of any two balls.
c)
At the centre of one of the ball.
d)
At the horizontal surface.
|
|
Neha Joshi answered |
The COM will be at the intersection point of the medians as that is the most symmetric point of this symmetric system.
Two bodies of masses m1 and m2 are moving such that their momentums are equal and opposite. The velocity of centre of mass of system of two bodies is:- a)cannot be determined.
- b)equal to the velocity of particle m1
- c)zero
- d)equal to the velocity of particle m2
Correct answer is option 'C'. Can you explain this answer?
Two bodies of masses m1 and m2 are moving such that their momentums are equal and opposite. The velocity of centre of mass of system of two bodies is:
a)
cannot be determined.
b)
equal to the velocity of particle m1
c)
zero
d)
equal to the velocity of particle m2
|
|
Gaurav Kumar answered |
As momentum is p = mv and a vector quantity, if both are moving in opposite direction then the net momentum will be mv –mv. The minus sign shows that it is in opposite direction.
So p(net) is 0.
So p(net) is 0.
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in- a)any direction
- b)horizontal direction
- c)same parabolic path
- d)vertical direction
Correct answer is option 'C'. Can you explain this answer?
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in
a)
any direction
b)
horizontal direction
c)
same parabolic path
d)
vertical direction
|
|
Riya Banerjee answered |
The internal forces have no effect on the trajectory of the center of mass, and the forces due to explosion are the internal forces. So the center of mass will follow the same parabolic path even after the explosion.
There are two blocks of mass 3 kg and 5 kg hanging from the ends of a rod of negligible mass. The rod is marked in eight equal parts as shown. At which of the points indicated should a string be attached if a rod is to remain horizontal when suspended from the string?

- a)D
- b)F
- c)B
- d)E
Correct answer is option 'D'. Can you explain this answer?
There are two blocks of mass 3 kg and 5 kg hanging from the ends of a rod of negligible mass. The rod is marked in eight equal parts as shown. At which of the points indicated should a string be attached if a rod is to remain horizontal when suspended from the string?


a)
D
b)
F
c)
B
d)
E

|
Ambition Institute answered |
This is based on torque balance, That is F.d=const.
Therefore 3×d=5×(8-d)
by solving we get d=5.
and at point 5=E
Therefore 3×d=5×(8-d)
by solving we get d=5.
and at point 5=E
Can you explain the answer of this question below:An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
- A:
y = +5 cm
- B:
y = +20 cm
- C:
y = -20 cm
- D:
y = -5 cm
The answer is d.
An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
y = +5 cm
y = +20 cm
y = -20 cm
y = -5 cm

|
Ambition Institute answered |
As the particle is exploded only due to its internal energy.
⇒ net external force during this process is 0 i.e. center mass will not change.
⇒ net external force during this process is 0 i.e. center mass will not change.
Let the particle while the explosion was above the origin of the coordinate system i.e. just before explosion xcm =0 and ycm =0
After the explosion, the Centre of mass will be at xcm =0 and ycm =0
Since smaller fragment has fallen on the y-axis.
Let positon of larger fragment be y.
Let positon of larger fragment be y.
m * ycm = (m/4 * 15) + (3m/4 * y)
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
Which of the following appliance works on the principle of moments.- a)pendulum clock
- b)Spring balance
- c)Balance wheel
- d)Beam balance
Correct answer is option 'D'. Can you explain this answer?
Which of the following appliance works on the principle of moments.
a)
pendulum clock
b)
Spring balance
c)
Balance wheel
d)
Beam balance
|
|
Arka Desai answered |
**Beam Balance**
The beam balance is the appliance that works on the principle of moments. It is a simple and commonly used device for measuring the weight of an object. The principle of moments, also known as the law of levers, states that for an object to be in equilibrium, the sum of the clockwise moments about any point must be equal to the sum of the anticlockwise moments about the same point.
**Working of a Beam Balance**
A beam balance consists of a beam, a pivot point, two pans, and a pointer or scale. The beam is a rigid bar that is supported at its center by a pivot point. The two pans are attached to the ends of the beam and are used to hold the objects whose weights are being compared. The pointer or scale is attached to the center of the beam and is used to indicate the balance or imbalance of the weights.
When the pans of the beam balance are empty, the beam is in equilibrium, which means that the clockwise moments are equal to the anticlockwise moments. This is because the distances of the empty pans from the pivot point are the same on both sides of the beam.
**Principle of Moments in Action**
When objects of different weights are placed on the pans, the beam becomes unbalanced. The heavier object creates a greater clockwise moment, while the lighter object creates a smaller anticlockwise moment. The beam tilts towards the side with the heavier object.
To restore equilibrium, weights are added or removed from one of the pans until the beam is level again. This adjustment ensures that the clockwise moments equal the anticlockwise moments, indicating that the weights on both pans are equal.
This balancing process demonstrates the principle of moments in action. By comparing the weights of different objects using a beam balance, we can determine which is heavier or lighter based on their effect on the balance.
**Conclusion**
In conclusion, the beam balance is the appliance that works on the principle of moments. It utilizes the principle of moments to compare the weights of objects and determine their relative heaviness or lightness. By understanding the principle of moments, we can accurately measure weights using this simple yet effective device.
The beam balance is the appliance that works on the principle of moments. It is a simple and commonly used device for measuring the weight of an object. The principle of moments, also known as the law of levers, states that for an object to be in equilibrium, the sum of the clockwise moments about any point must be equal to the sum of the anticlockwise moments about the same point.
**Working of a Beam Balance**
A beam balance consists of a beam, a pivot point, two pans, and a pointer or scale. The beam is a rigid bar that is supported at its center by a pivot point. The two pans are attached to the ends of the beam and are used to hold the objects whose weights are being compared. The pointer or scale is attached to the center of the beam and is used to indicate the balance or imbalance of the weights.
When the pans of the beam balance are empty, the beam is in equilibrium, which means that the clockwise moments are equal to the anticlockwise moments. This is because the distances of the empty pans from the pivot point are the same on both sides of the beam.
**Principle of Moments in Action**
When objects of different weights are placed on the pans, the beam becomes unbalanced. The heavier object creates a greater clockwise moment, while the lighter object creates a smaller anticlockwise moment. The beam tilts towards the side with the heavier object.
To restore equilibrium, weights are added or removed from one of the pans until the beam is level again. This adjustment ensures that the clockwise moments equal the anticlockwise moments, indicating that the weights on both pans are equal.
This balancing process demonstrates the principle of moments in action. By comparing the weights of different objects using a beam balance, we can determine which is heavier or lighter based on their effect on the balance.
**Conclusion**
In conclusion, the beam balance is the appliance that works on the principle of moments. It utilizes the principle of moments to compare the weights of objects and determine their relative heaviness or lightness. By understanding the principle of moments, we can accurately measure weights using this simple yet effective device.
Which of the following options are correct,
where i, j and k are unit vectors along the x, y and z axis?- a)i.j = 1 ; j x i =0
- b)i.j = 0 ; j x i = -k
- c)i.j = 1 ; j x i = -k
- d)i.j = 1 ; j x i = k
Correct answer is option 'B'. Can you explain this answer?
Which of the following options are correct,
where i, j and k are unit vectors along the x, y and z axis?
where i, j and k are unit vectors along the x, y and z axis?
a)
i.j = 1 ; j x i =0
b)
i.j = 0 ; j x i = -k
c)
i.j = 1 ; j x i = -k
d)
i.j = 1 ; j x i = k
|
|
Hansa Sharma answered |
Dot product of two different unit vectors is 0 and dot product of two same unit vectors is 1. Cross product of two different unit vectors taken according to right hand thumb rule is the other vector. Cross product of two same unit vectors is 0.
A meter rule is supported at its centre. It is balanced by two weights, A and B. If A and B are placed at a distance 20 cm, and 40 cm from the centre of scale, find the weight of B. The weight of A is 50N.
- a)30 N
- b)40 N
- c)25 N
- d)20 N
Correct answer is option 'C'. Can you explain this answer?
A meter rule is supported at its centre. It is balanced by two weights, A and B. If A and B are placed at a distance 20 cm, and 40 cm from the centre of scale, find the weight of B. The weight of A is 50N.
a)
30 N
b)
40 N
c)
25 N
d)
20 N
|
|
Gaurav Kumar answered |
In balanced condition torque of the both sides must be equal so Fa × Da = Fb × Db
50 × 20 = Fb × 40
Fb = 25 N
50 × 20 = Fb × 40
Fb = 25 N
If the net force acting on the system of particles is zero, then which of the following may vary
- a)moment of inertia
- b)Kinetic energy of the system
- c)velocity of centre of mass
- d)position of centre of mass
Correct answer is option 'D'. Can you explain this answer?
If the net force acting on the system of particles is zero, then which of the following may vary
a)
moment of inertia
b)
Kinetic energy of the system
c)
velocity of centre of mass
d)
position of centre of mass
|
|
Suresh Kumar answered |
Correct answer is B . because when a=0 then v=constant hence K.E. will be constant and position of com will vary
A child sits stationary at one end of long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in the forward direction with speed u. The centre of mass of the system (child + trolley) will move with speed- a)v
- b)zero
- c)u + v
- d)v/u
Correct answer is option 'A'. Can you explain this answer?
A child sits stationary at one end of long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in the forward direction with speed u. The centre of mass of the system (child + trolley) will move with speed
a)
v
b)
zero
c)
u + v
d)
v/u
|
|
Preeti Iyer answered |
The child is running arbitrarily on a trolley moving with velocity v. However, the running of the child will produce no effect on the velocity of the centre of mass of the trolley. This is because the force due to the boy’s motion is purely internal. Internal forces produce no effect on the motion of the bodies on which they act. Since no external force is involved in the boy–trolley system, the boy’s motion will produce no change in the velocity of the centre of mass of the trolley.
The rotational analog to the expression F = ma in linear motion is ___________in rotational motion.- a)τ = mα
- b)F= Iα
- c)τ = Iα
- d)F = mα
Correct answer is option 'C'. Can you explain this answer?
The rotational analog to the expression F = ma in linear motion is ___________in rotational motion.
a)
τ = mα
b)
F= Iα
c)
τ = Iα
d)
F = mα
|
|
Preeti Iyer answered |
Force (in linear) = torque (in rotational)
Mass (in linear motion) = moment of inertia ( l ) (in rotational motion)
Acceleration(a) (in linear) = angular acceleration (α) (in rotational)
F = ma (in linear) and torque = Iα (in rotational)
Mass (in linear motion) = moment of inertia ( l ) (in rotational motion)
Acceleration(a) (in linear) = angular acceleration (α) (in rotational)
F = ma (in linear) and torque = Iα (in rotational)
A stone of mass m tied to a string of length l is rotating along a circular path with constant speed v. The torque on the stone is- a)zero
- b)mvl
- c)mv/l
- d)mv2/l
Correct answer is option 'A'. Can you explain this answer?
A stone of mass m tied to a string of length l is rotating along a circular path with constant speed v. The torque on the stone is
a)
zero
b)
mvl
c)
mv/l
d)
mv2/l
|
|
Preeti Iyer answered |
Hence the torque is zero .Because the line of action of the tension passes through the centre .So lever arm of tension is zero So the torque acting is also zero .
Five forces are separately applied to a flat object lying on a table of negligible friction as shown in figure. The force which will not cause the object to rotate about the centre of the object is

- a)F2
- b)F3
- c)F4
- d)F1
Correct answer is option 'A'. Can you explain this answer?
Five forces are separately applied to a flat object lying on a table of negligible friction as shown in figure. The force which will not cause the object to rotate about the centre of the object is


a)
F2
b)
F3
c)
F4
d)
F1
|
|
Gaurav Kumar answered |
The line of action of F2 passes through the centre of rotation, and thus cannot produce a torque about the centre (r = 0).
Three identical spheres each of radius R are placed such that their centres lie on a straight line. What is the location of their centre of mass from the centre of the first sphere?
- a)R
- b)2R
- c)3R
- d)4R
Correct answer is option 'B'. Can you explain this answer?
Three identical spheres each of radius R are placed such that their centres lie on a straight line. What is the location of their centre of mass from the centre of the first sphere?
a)
R
b)
2R
c)
3R
d)
4R
|
|
Geetika Shah answered |
- Distance between first and last sphere = R + 2R + R = 4R
- Since the spheres are identical and lie in a straight line, the centre of mass will lie exactly in the middle.
- Hence the centre of mass lies at a distance of 2R from the centre of the first sphere.
The sum of moments of masses of all the particles in a system about the centre of mass is always:- a)maximum
- b)infinite
- c)zero
- d)minimum
Correct answer is option 'C'. Can you explain this answer?
The sum of moments of masses of all the particles in a system about the centre of mass is always:
a)
maximum
b)
infinite
c)
zero
d)
minimum
|
|
Neha Sharma answered |
In physics, the center of mass of a distribution of mass in space is the unique point where the weighted relative position of the distributed mass sums to zero, or the point where if a force is applied it moves in the direction of the force without rotating. The distribution of mass is balanced around the center of mass and the average of the weighted position coordinates of the distributed mass defines its coordinates. Calculations in mechanics are often simplified when formulated with respect to the center of mass.
In order to rotate a body, we need to apply- a)two forces at two ends but in the same direction
- b)a large force at any point on the body
- c)Two equal forces at two ends but in the opposite direction
- d)a small force but exactly at its centre of gravity
Correct answer is option 'C'. Can you explain this answer?
In order to rotate a body, we need to apply
a)
two forces at two ends but in the same direction
b)
a large force at any point on the body
c)
Two equal forces at two ends but in the opposite direction
d)
a small force but exactly at its centre of gravity
|
|
Lavanya Menon answered |
In order to rotate a body, we need to apply two equal forces at two ends but in the opposite direction.
There are two particles of masses m and 2m placed at a distance‘d’ apart on a smooth horizontal surface. Where will the collision occur (with respect to original positions), if they are allowed to move towards each other because of their mutual attraction?- a)2d/3
- b)d/2
- c)2d
- d)d
Correct answer is option 'A'. Can you explain this answer?
There are two particles of masses m and 2m placed at a distance‘d’ apart on a smooth horizontal surface. Where will the collision occur (with respect to original positions), if they are allowed to move towards each other because of their mutual attraction?
a)
2d/3
b)
d/2
c)
2d
d)
d
|
|
Pooja Shah answered |
Their collision will occur at their center of mass.
If we consider body of mass 'm' at origin & '2m' at distance "d" from 1st body on X-axis then, center of mass,
X = m1(x1)+m2(x2)/m1+m2
X = m(0)+2m(d)/m+2m
X = 2md/3m
X = 2d/3
Hence A is the correct answer.
If we consider body of mass 'm' at origin & '2m' at distance "d" from 1st body on X-axis then, center of mass,
X = m1(x1)+m2(x2)/m1+m2
X = m(0)+2m(d)/m+2m
X = 2md/3m
X = 2d/3
Hence A is the correct answer.
When a fire cracker initially at rest, explodes into a number of fragments, the centre of mass- a)remains stationary
- b)moves along a parabolic path
- c)moves along vertical direction
- d)moves along horizontal direction
Correct answer is option 'A'. Can you explain this answer?
When a fire cracker initially at rest, explodes into a number of fragments, the centre of mass
a)
remains stationary
b)
moves along a parabolic path
c)
moves along vertical direction
d)
moves along horizontal direction
|
|
Om Desai answered |
When a fire cracker initially at rest, explodes into a number of fragments, the centre of mass remains stationary. This is analogous to the explosion of a ball while it is flying in a trajectory.
Determine the force that must be applied to end of the class 1 lever shown below to lift the 500 lb load.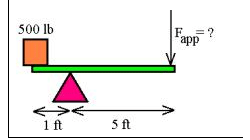
- a)500 lb
- b)2500 lb
- c)5 lb
- d)100 lb
Correct answer is option 'D'. Can you explain this answer?
Determine the force that must be applied to end of the class 1 lever shown below to lift the 500 lb load.
a)
500 lb
b)
2500 lb
c)
5 lb
d)
100 lb

|
Piyali Das answered |
Balance the 2 opp moments on the 2 sides
you will get the ans
1×500=F×5
that is
F=100
you will get the ans
1×500=F×5
that is
F=100
Every point in a rotating rigid body has the same __________at any instant of time.
- a)linear velocity
- b)angular velocity
- c)displacement
- d)linear momentum
Correct answer is option 'B'. Can you explain this answer?
Every point in a rotating rigid body has the same __________at any instant of time.
a)
linear velocity
b)
angular velocity
c)
displacement
d)
linear momentum
|
|
Preeti Iyer answered |
Every point in any rigid rotating object is rotating at the same angular velocity. However, there are a few cases where people have used the term "angular velocity" when they really meant tangential velocity, so you do have to be careful.
A wheel having moment of inertia 3.5 kgm2 rotates about the vertical axis. The torque required to produce an angular acceleration of 25rad/s2 in the wheel is- a)8.45Nm
- b)85Nm
- c)88.5Nm
- d)87.5Nm
Correct answer is option 'D'. Can you explain this answer?
A wheel having moment of inertia 3.5 kgm2 rotates about the vertical axis. The torque required to produce an angular acceleration of 25rad/s2 in the wheel is
a)
8.45Nm
b)
85Nm
c)
88.5Nm
d)
87.5Nm
|
|
Pooja Shah answered |
Torque = moment of inertia × angular acceleration
3.5 × 25 =87.5 Nm
3.5 × 25 =87.5 Nm
The general motion of a rigid body consists of
- a)translational motion only
- b)rotational motion only
- c)both, translational and rotational motion
- d)does not include translational and rotational motions
Correct answer is option 'C'. Can you explain this answer?
The general motion of a rigid body consists of
a)
translational motion only
b)
rotational motion only
c)
both, translational and rotational motion
d)
does not include translational and rotational motions
|
|
Arun Khanna answered |
The general motion of a rigid body consists of both, translational and rotational motion. This is much obvious as it is seen all around us.
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls, while in air- a)depend on the speeds of the two balls
- b)depend on the masses of the two balls
- c)depend on the direction of the motion of the balls
- d)is equal to g
Correct answer is option 'D'. Can you explain this answer?
Two balls are thrown simultaneously in air. The acceleration of the centre of mass of the two balls, while in air
a)
depend on the speeds of the two balls
b)
depend on the masses of the two balls
c)
depend on the direction of the motion of the balls
d)
is equal to g
|
|
Mira Sharma answered |
The only force acting on the balls is force of gravity, so the acceleration of centre of mass is equal to g.
A proton and an electron, initially at rest, are allowed to move under their mutal attractive force. Their centre of mass will:- a)move towards the proton
- b)move towards the electron
- c)move in an unpredictable manner
- d)remain stationary
Correct answer is option 'D'. Can you explain this answer?
A proton and an electron, initially at rest, are allowed to move under their mutal attractive force. Their centre of mass will:
a)
move towards the proton
b)
move towards the electron
c)
move in an unpredictable manner
d)
remain stationary
|
|
Arya Dasgupta answered |
Explanation:
When a proton and an electron are allowed to move under their mutual attractive force, their centre of mass remains stationary. This can be explained by the following factors:
1. Conservation of momentum: According to Newton's third law, the forces acting on the proton and electron are equal and opposite. Therefore, the momentum gained by the proton is equal and opposite to the momentum gained by the electron. As a result, the total momentum of the system remains zero, which means the centre of mass remains stationary.
2. Mass ratio: The mass of the proton is much larger than the mass of the electron. Therefore, the proton moves much less than the electron towards the centre of mass. This means that the centre of mass is closer to the proton, but still remains stationary.
3. Distance between the particles: The force of attraction between the proton and electron is inversely proportional to the square of the distance between them. As the particles move towards each other, the force of attraction increases, which causes an acceleration in both particles. However, since the force also decreases as the particles get closer, the acceleration decreases. This means that the particles move towards each other at an ever-decreasing speed, and eventually come to a stop at a fixed distance from each other. At this point, the centre of mass remains stationary.
Therefore, the correct answer is option 'D': the centre of mass remains stationary.
When a proton and an electron are allowed to move under their mutual attractive force, their centre of mass remains stationary. This can be explained by the following factors:
1. Conservation of momentum: According to Newton's third law, the forces acting on the proton and electron are equal and opposite. Therefore, the momentum gained by the proton is equal and opposite to the momentum gained by the electron. As a result, the total momentum of the system remains zero, which means the centre of mass remains stationary.
2. Mass ratio: The mass of the proton is much larger than the mass of the electron. Therefore, the proton moves much less than the electron towards the centre of mass. This means that the centre of mass is closer to the proton, but still remains stationary.
3. Distance between the particles: The force of attraction between the proton and electron is inversely proportional to the square of the distance between them. As the particles move towards each other, the force of attraction increases, which causes an acceleration in both particles. However, since the force also decreases as the particles get closer, the acceleration decreases. This means that the particles move towards each other at an ever-decreasing speed, and eventually come to a stop at a fixed distance from each other. At this point, the centre of mass remains stationary.
Therefore, the correct answer is option 'D': the centre of mass remains stationary.
Masses 1 kg, 1.5 kg, 2 kg, and “M” kg are situated at (2,1,1), (1,2,1), (2,-2,1) and (-1,4,3). What is the value of “M” if their centre of mass is at (1,1,3/2)?- a)1 kg
- b)1.5 kg
- c)2 kg
- d)2.5 kg
Correct answer is option 'B'. Can you explain this answer?
Masses 1 kg, 1.5 kg, 2 kg, and “M” kg are situated at (2,1,1), (1,2,1), (2,-2,1) and (-1,4,3). What is the value of “M” if their centre of mass is at (1,1,3/2)?
a)
1 kg
b)
1.5 kg
c)
2 kg
d)
2.5 kg
|
|
Tejas Verma answered |
Sum of masses = 1 + 1.5 + 2 + M = 4.5 + M
x-coordinate;
(1*2 + 1.5*1 + 2*2 – M)/(4.5 + M) = 1
4.5 + M = 7.5 – M
2M = 3
M = 1.5 kg.
x-coordinate;
(1*2 + 1.5*1 + 2*2 – M)/(4.5 + M) = 1
4.5 + M = 7.5 – M
2M = 3
M = 1.5 kg.
For an object with the centre of mass at the origin, the x-coordinates of particles of the object _____.
- a)maybe all positive.
- b)maybe all negative.
- c)maybe all non-negative.
- d)cannot be predicted.
Correct answer is option 'C'. Can you explain this answer?
For an object with the centre of mass at the origin, the x-coordinates of particles of the object _____.
a)
maybe all positive.
b)
maybe all negative.
c)
maybe all non-negative.
d)
cannot be predicted.
|
|
Tejas Verma answered |
- For an object to have the x-coordinate of its centre of mass, there should be particles on both the negative and positive coordinates of the plane for the sum to be zero.
- However, for 1-dimensional particles that all lie on the y-axis symmetric about the x-axis, the x-coordinate is zero – which is neither positive nor negative, i.e., non-negative.
Which of the following represents the correct relationship between angular displacement and torque?- a)Inverse proportionality
- b)Equal magnitude
- c)None of the mentioned
- d)Direct proportionality
Correct answer is option 'D'. Can you explain this answer?
Which of the following represents the correct relationship between angular displacement and torque?
a)
Inverse proportionality
b)
Equal magnitude
c)
None of the mentioned
d)
Direct proportionality
|
|
Raghavendra Ghoshal answered |
Angular displacement and torque are two different concepts in physics that are related to the rotational motion of an object. The correct relationship between these two quantities is described by the option "D", which states that they are directly proportional to each other.
**Angular Displacement:**
- Angular displacement is a measure of the change in the orientation or position of an object undergoing rotational motion.
- It is defined as the angle through which an object rotates in a given time interval.
- Angular displacement is usually measured in radians (rad) or degrees (°).
**Torque:**
- Torque, also known as the moment of force, is a measure of the tendency of a force to cause rotational motion.
- It is defined as the product of the force applied to an object and the distance from the point of rotation to the line of action of the force.
- Torque is usually measured in newton-meters (Nm) or foot-pounds (ft-lb).
**The Relationship:**
The relationship between angular displacement and torque can be understood by considering the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's
**Angular Displacement:**
- Angular displacement is a measure of the change in the orientation or position of an object undergoing rotational motion.
- It is defined as the angle through which an object rotates in a given time interval.
- Angular displacement is usually measured in radians (rad) or degrees (°).
**Torque:**
- Torque, also known as the moment of force, is a measure of the tendency of a force to cause rotational motion.
- It is defined as the product of the force applied to an object and the distance from the point of rotation to the line of action of the force.
- Torque is usually measured in newton-meters (Nm) or foot-pounds (ft-lb).
**The Relationship:**
The relationship between angular displacement and torque can be understood by considering the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's second law, known as the rotational analog of Newton's
For a system to be in equilibrium, the net torques acting on it must balance. This is true only if the torque are taken about
- a)The centre of mass of system.
- b)The centre of the system.
- c)any point on the system
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
For a system to be in equilibrium, the net torques acting on it must balance. This is true only if the torque are taken about
a)
The centre of mass of system.
b)
The centre of the system.
c)
any point on the system
d)
None of these
|
|
Yash Ghoshal answered |
For a system to be in equilibrium, the net torques acting on it must indeed balance. This condition of equilibrium applies when calculating torques about any point on or outside the system, not just specific locations like the center of the system or its center of mass. This principle is a fundamental aspect of rotational dynamics and equilibrium analysis in physics.
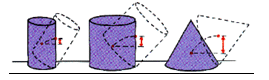
Arrange the comparative stabilities of the three objects shown in the figure in terms of work and potential energy.
- a)2nd object < 3rd object < 1st object
- b)3rd object < 1st object < 2nd object
- c)1st object < 2nd object < 3rd object
- d)1st object < 3rd object < 2nd object
Correct answer is option 'C'. Can you explain this answer?
Arrange the comparative stabilities of the three objects shown in the figure in terms of work and potential energy.
a)
2nd object < 3rd object < 1st object
b)
3rd object < 1st object < 2nd object
c)
1st object < 2nd object < 3rd object
d)
1st object < 3rd object < 2nd object
|
|
Neha Joshi answered |
A object’s stability depends upon its centre of gravity.the larger the centre of gravity the more stable,By looking at the figures we can easily figure out which is more stable.
A radioactive nucleus of mass M moving along the positive x-direction with speed v emits an alpha particle of mass m. If the alpha particle proceeds along the positive y-direction, the centre of mass of the system (made of the daughter nucleus and the alpha particle) will:- a)move along the positive x-direction with speed equal to v
- b)remain at rest
- c)move along the positive x-direction with speed less than v
- d)move along the positive x-direction with speed greater than v
Correct answer is option 'A'. Can you explain this answer?
A radioactive nucleus of mass M moving along the positive x-direction with speed v emits an alpha particle of mass m. If the alpha particle proceeds along the positive y-direction, the centre of mass of the system (made of the daughter nucleus and the alpha particle) will:
a)
move along the positive x-direction with speed equal to v
b)
remain at rest
c)
move along the positive x-direction with speed less than v
d)
move along the positive x-direction with speed greater than v
|
|
Simran Chauhan answered |
The momentum of the initial particle remains conserved. Hence the emitted particles’ COM will remain along +ve x-axis.
When no external Torque acts on a system, what is conserved- a)Energy
- b)Force
- c)Angular momentum
- d)Linear momentum
Correct answer is option 'C'. Can you explain this answer?
When no external Torque acts on a system, what is conserved
a)
Energy
b)
Force
c)
Angular momentum
d)
Linear momentum
|
|
Nandini Iyer answered |
The law of conservation of angular momentum states that when no external torque acts on an object, no change of angular momentum will occur of course not torque is the rate of change of angular momentum and angular momentum in simple sense can be seen as the product of angular velocity with moment of inertia. Changing angular velocities are behind spin skating, toe dancing etc.
example:
on a disk M and radius R rotating with angular speed ωi drops a small object
of mass m on the edge of disk
before
Mif=Iiωi=1/2MR^2ωi
after
Mf=Ifωf=(1/MR^2+mR^2)ωf
it must be
1/2MR^2ωi=(1/MR^2+mR^2)ωf
then
ωf=ωi(1/2MR^2)/(1/MR^2+mR^2)
Two particles A and B of mass ‘m’ move towards each other under a mutual force of attraction. If velocity of A is 2 v and that of B is v, calculate the velocity of centre of mass of the system.- a)v/2
- b)zero
- c)3v
- d)v
Correct answer is option 'B'. Can you explain this answer?
Two particles A and B of mass ‘m’ move towards each other under a mutual force of attraction. If velocity of A is 2 v and that of B is v, calculate the velocity of centre of mass of the system.
a)
v/2
b)
zero
c)
3v
d)
v

|
Arnav Chawla answered |
M and 2m respectively are moving towards each other with velocities v and 2v respectively. After collision, A comes to rest. Find the velocity of B after the collision.
The centre of masses of two particles with masses 2 kg and 1 kg located at (1,0,1) and (2,2,0) is located at:- a)4/3, 2/3, 2/3
- b)2/3, 4/3, 2/3
- c)2/3, 2/3, 4/3
- d)1/3, 2/3, 2/3
Correct answer is option 'A'. Can you explain this answer?
The centre of masses of two particles with masses 2 kg and 1 kg located at (1,0,1) and (2,2,0) is located at:
a)
4/3, 2/3, 2/3
b)
2/3, 4/3, 2/3
c)
2/3, 2/3, 4/3
d)
1/3, 2/3, 2/3
|
|
Tejas Verma answered |
Sum of masses = 2 + 1 = 3
x-coordinate;
(2*1 + 1*2)/3 = 4/3
y-coordinate;
(2*0 + 1*2)/3 = 2/3
z-coordinate;
(2*1 + 1*0)/3 = 2/3.
x-coordinate;
(2*1 + 1*2)/3 = 4/3
y-coordinate;
(2*0 + 1*2)/3 = 2/3
z-coordinate;
(2*1 + 1*0)/3 = 2/3.
A shell following a parabolic path explodes somewhere in its flight. The centre of mass of fragments will continue to move in- a)Any direction
- b)Vertical direction
- c)Same parabolic path
- d)Horizontal direction
Correct answer is option 'C'. Can you explain this answer?
A shell following a parabolic path explodes somewhere in its flight. The centre of mass of fragments will continue to move in
a)
Any direction
b)
Vertical direction
c)
Same parabolic path
d)
Horizontal direction

|
Rohit Joshi answered |
Ans.
Option (c)
The internal forces have no effect on the trajectory of centre of mass, and the forces due to explosion are the internal forces. So the centre of mass will follow the same parabolic path even after explosion.
Chapter doubts & questions for Equilibrium of Forces - Physics for JAMB 2025 is part of JAMB exam preparation. The chapters have been prepared according to the JAMB exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JAMB 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Equilibrium of Forces - Physics for JAMB in English & Hindi are available as part of JAMB exam.
Download more important topics, notes, lectures and mock test series for JAMB Exam by signing up for free.
Physics for JAMB
259 videos|253 docs|230 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup


 are
are